数学:3.1相似的图形教案(湘教版九年级上)
文档属性
| 名称 | 数学:3.1相似的图形教案(湘教版九年级上) |
|
|
| 格式 | rar | ||
| 文件大小 | 28.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-10-22 15:15:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
3.1相似的图形
教学目标
目的与要求 通过一些相似的实例,理解相似的概念,正确地区分出哪些是相似的图形,哪些不是相似图形.
知识与技能 了解相似的概念,能按要求作出简单图形的相似图形.
情感、态度与价值观 在观察、操作、推理等探索过程中,体验
数学活动充满探索性和创造性,通过一些相似的实例去体会感受生活中的相似.
教学过程
相似的图形
日常生活中我们会碰到很多这种形状相同、大小不一定相同的图形,在数学上,我们把具有相同形状的图形称为相似形.
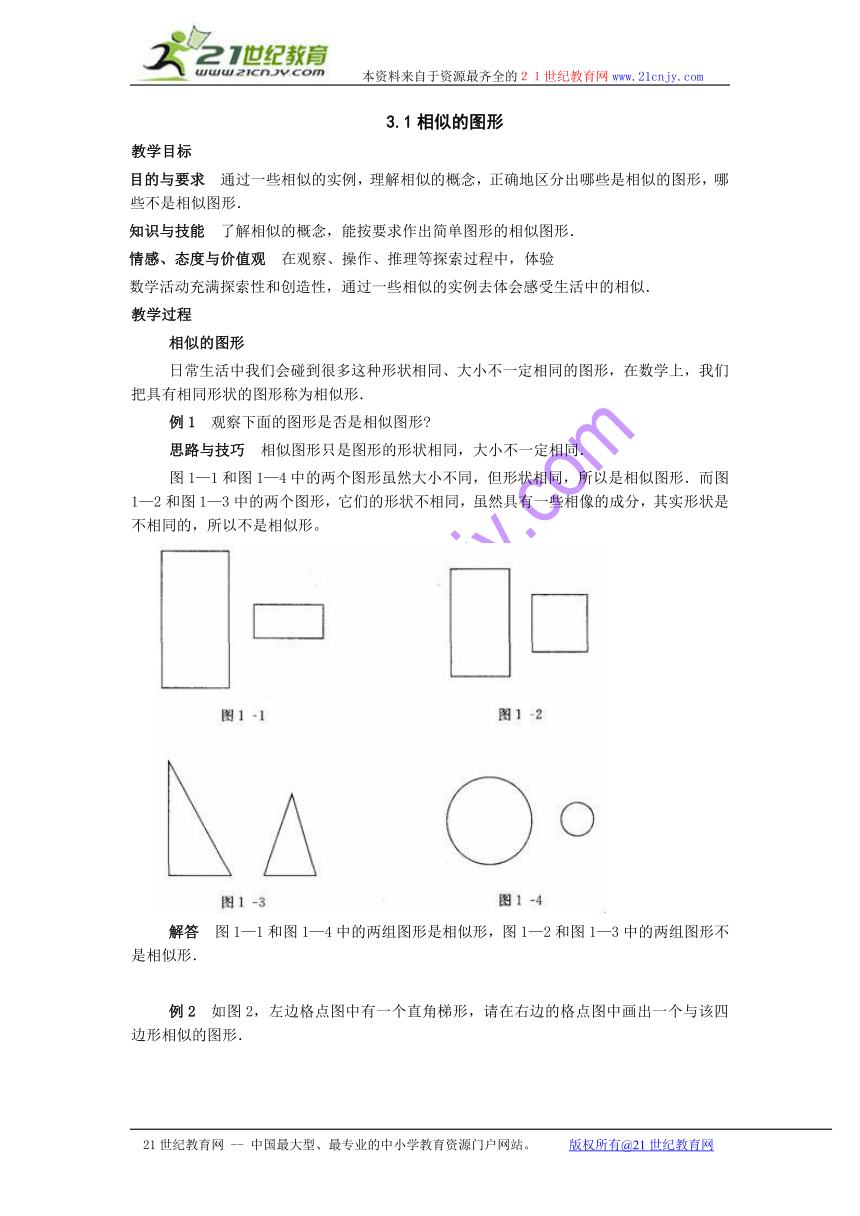
例1 观察下面的图形是否是相似图形
思路与技巧 相似图形只是图形的形状相同,大小不一定相同.
图1—1和图1—4中的两个图形虽然大小不同,但形状相同,所以是相似图形.而图1—2和图1—3中的两个图形,它们的形状不相同,虽然具有一些相像的成分,其实形状是不相同的,所以不是相似形。
解答 图1—1和图1—4中的两组图形是相似形,图1—2和图1—3中的两组图形不是相似形.
例2 如图2,左边格点图中有一个直角梯形,请在右边的格点图中画出一个与该四边形相似的图形.
思路与技巧 画相似图形时,要注意对应位置上的线段要放大或缩小相同的倍数,对应的角的大小不变,这样画出的图形才可能与原图形相似.
解答 如图3所示.
评注 此题答案不惟一,可由相对应的线段放大或缩小不同的倍数,得到多个不同的答案.
【探究活动】
提出问题 有一张正方形纸片,第1次把它分割成4片与原纸片相似的纸片,第2次把其中的一片再如此分成4片,以后每一次都把前面所得的其中—片分割成4片.如此进行下去,试问:
(1)经过5次分割后,共得到多少张纸片
(2)经n次分割后,共得到多少张纸片
(3)能否经过若干次分割后,共得到2003张纸片
探究准备 一张较大的正方形白纸,一把直尺,刀片.
探究过程 用直尺按要求折纸,并用刀片裁剪.由于每次分割后,1片变成4片,增3片,经5次分割后,共增(3×5)15片,故共得(1+15)16片;经n次分割后,共增3n片,故共得(1+3n)片;注意到2003=3×667+2不能写成3n十1形式,故不可能经若干次分割后得到2003张纸片.
探究评析 从探究过程可知:每次分割,增加3张纸片,所以分割n次,共得(1+3n)张纸片——这就是解决本题的关键,循此规律可方便地解决问题(3).
例3 把一张纸剪成5块,从其中取出一块,再把每一块剪成5块,再从其中取出1块,再剪成5块……,这样依次地剪下去,剪完某一次停止,共得纸片块数可能是 ( )
A.2002 B.2003 C.2005 D.2008
思路与技巧 根据上面探究问题的方法,每剪—次增加4片,故n次分割后,共增4n片,故共得(1+4n)片,注意到2005=4×501+1,能写成(4n+1)的形式,故是可能的;而2002、2003、2008不能写成4n+1的形式,故是不可能的.
解答 选C
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
3.1相似的图形
教学目标
目的与要求 通过一些相似的实例,理解相似的概念,正确地区分出哪些是相似的图形,哪些不是相似图形.
知识与技能 了解相似的概念,能按要求作出简单图形的相似图形.
情感、态度与价值观 在观察、操作、推理等探索过程中,体验
数学活动充满探索性和创造性,通过一些相似的实例去体会感受生活中的相似.
教学过程
相似的图形
日常生活中我们会碰到很多这种形状相同、大小不一定相同的图形,在数学上,我们把具有相同形状的图形称为相似形.
例1 观察下面的图形是否是相似图形
思路与技巧 相似图形只是图形的形状相同,大小不一定相同.
图1—1和图1—4中的两个图形虽然大小不同,但形状相同,所以是相似图形.而图1—2和图1—3中的两个图形,它们的形状不相同,虽然具有一些相像的成分,其实形状是不相同的,所以不是相似形。
解答 图1—1和图1—4中的两组图形是相似形,图1—2和图1—3中的两组图形不是相似形.
例2 如图2,左边格点图中有一个直角梯形,请在右边的格点图中画出一个与该四边形相似的图形.
思路与技巧 画相似图形时,要注意对应位置上的线段要放大或缩小相同的倍数,对应的角的大小不变,这样画出的图形才可能与原图形相似.
解答 如图3所示.
评注 此题答案不惟一,可由相对应的线段放大或缩小不同的倍数,得到多个不同的答案.
【探究活动】
提出问题 有一张正方形纸片,第1次把它分割成4片与原纸片相似的纸片,第2次把其中的一片再如此分成4片,以后每一次都把前面所得的其中—片分割成4片.如此进行下去,试问:
(1)经过5次分割后,共得到多少张纸片
(2)经n次分割后,共得到多少张纸片
(3)能否经过若干次分割后,共得到2003张纸片
探究准备 一张较大的正方形白纸,一把直尺,刀片.
探究过程 用直尺按要求折纸,并用刀片裁剪.由于每次分割后,1片变成4片,增3片,经5次分割后,共增(3×5)15片,故共得(1+15)16片;经n次分割后,共增3n片,故共得(1+3n)片;注意到2003=3×667+2不能写成3n十1形式,故不可能经若干次分割后得到2003张纸片.
探究评析 从探究过程可知:每次分割,增加3张纸片,所以分割n次,共得(1+3n)张纸片——这就是解决本题的关键,循此规律可方便地解决问题(3).
例3 把一张纸剪成5块,从其中取出一块,再把每一块剪成5块,再从其中取出1块,再剪成5块……,这样依次地剪下去,剪完某一次停止,共得纸片块数可能是 ( )
A.2002 B.2003 C.2005 D.2008
思路与技巧 根据上面探究问题的方法,每剪—次增加4片,故n次分割后,共增4n片,故共得(1+4n)片,注意到2005=4×501+1,能写成(4n+1)的形式,故是可能的;而2002、2003、2008不能写成4n+1的形式,故是不可能的.
解答 选C
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
