22.3 实际问题与二次函数 同步练习(含答案)2024-2025学年人教版数学九年级上册
文档属性
| 名称 | 22.3 实际问题与二次函数 同步练习(含答案)2024-2025学年人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 358.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-17 00:00:00 | ||
图片预览




文档简介
22.3 实际问题与二次函数 同步练习2024-2025学年人教版数学九年级上册
一、单选题
1.在一个边长为2的正方形中挖去一个边长为x(0<x<2)的小正方形,如果设剩余部分的面积为y,那么y关于x的函数解析式是( )
A. B. C. D.
2.拱桥的形状是抛物线,其函数关系式为,当水面离桥顶的高度为m时,水面的宽度为( )米.
A.8 B.9 C.10 D.11
3.在羽毛球比赛中,某次羽毛球的运动路线呈抛物线形,羽毛球距地面的高度 与水平距离 之间的关系如图所示,点B为落地点,且 , ,羽毛球到达的最高点到y轴的距离为 ,那么羽毛球到达最高点时离地面的高度为( )
A. B. C. D.
4.如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )
A. B.
C. D.
5.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如表:下列结论错误的是( )
t 0 1 2 3 4 5 6 7 …
h 0 8 14 18 20 20 18 14 …
A.足球距离地面的最大高度超过20m
B.足球飞行路线的对称轴是直线
C.点(10,0)在该抛物线上
D.足球被踢出时,距离地面的高度逐渐下降.
6.如图,四边形中,,若,则四边形的面积最大值是( )
A.4 B.6 C.8 D.10
7.如图,是等腰直角三角形,,,点为边上一点,过点作,,垂足分别为,,点从点出发沿运动至点.设,,四边形的面积为,在运动过程中,下列说法正确的是( )
A.y与x满足一次函数关系,S与x满足二次函数关系,且S存在最大值
B.y与x满足一次函数关系,S与x满足二次函数关系,且S存在最小值
C.y与x满足反比例函数关系,S与x满足二次函数关系,且S存在最大值
D.y与x满足反比例函数关系,S与x满足二次函数关系,且S存在最小值
8.据省统计局公布的数据,合肥市2021年第一季度GDP总值约为2.4千亿元人民币,若我市第三季度GDP总值为y千亿元人民币,平均每个季度GDP增长的百分率为x,则y关于x的函数表达式是( )
A.y=2.4(1+2x) B.y=2.4(1-x)2
C.y=2.4(1+x)2 D.y=2.4+2.4(1+x)+2.4(1+x)2
二、填空题
9.原价为160元的电器连续两次降价后的价格为y元,若平均每次降价的百分率是x,则y与x的函数表达式为 .
10.一小球被抛出后,距离地面的高度h(米)和飞行时间t(秒)满足下面函数关系式,则小球距离地面的最大高度是 米.
11.在一个边长为2的正方形中挖去一个小正方形,使小正方形四周剩下部分的宽度均为x,若剩下阴影部分的面积为y,那么y关于x的函数解析式是 .
12.以40m/s的速度将小球沿与地面成30度角的方向击出时,球的飞行路线是一条抛物线.如果不考虑空气阻力,球的飞行高度h(单位m)与飞行时间t(单位s)之间具有函数关系:h=20t﹣5t2,那么球从飞出到落地要用的时间是 s.
13.如图,正方形 的边长为4, 、 、 、 分别是边 、 、 、 上的动点, .则四边形 面积的最小值为 .
14.如图,人工喷泉有一个竖直的喷水枪 ,喷水口A距地面 ,喷出水流的运动路线是抛物线,如果水流的最高点P到喷水枪 所在直线的距离为 ,且到地面的距离为 ,则水流的落地点C到水枪底部B的距离为 .
三、解答题
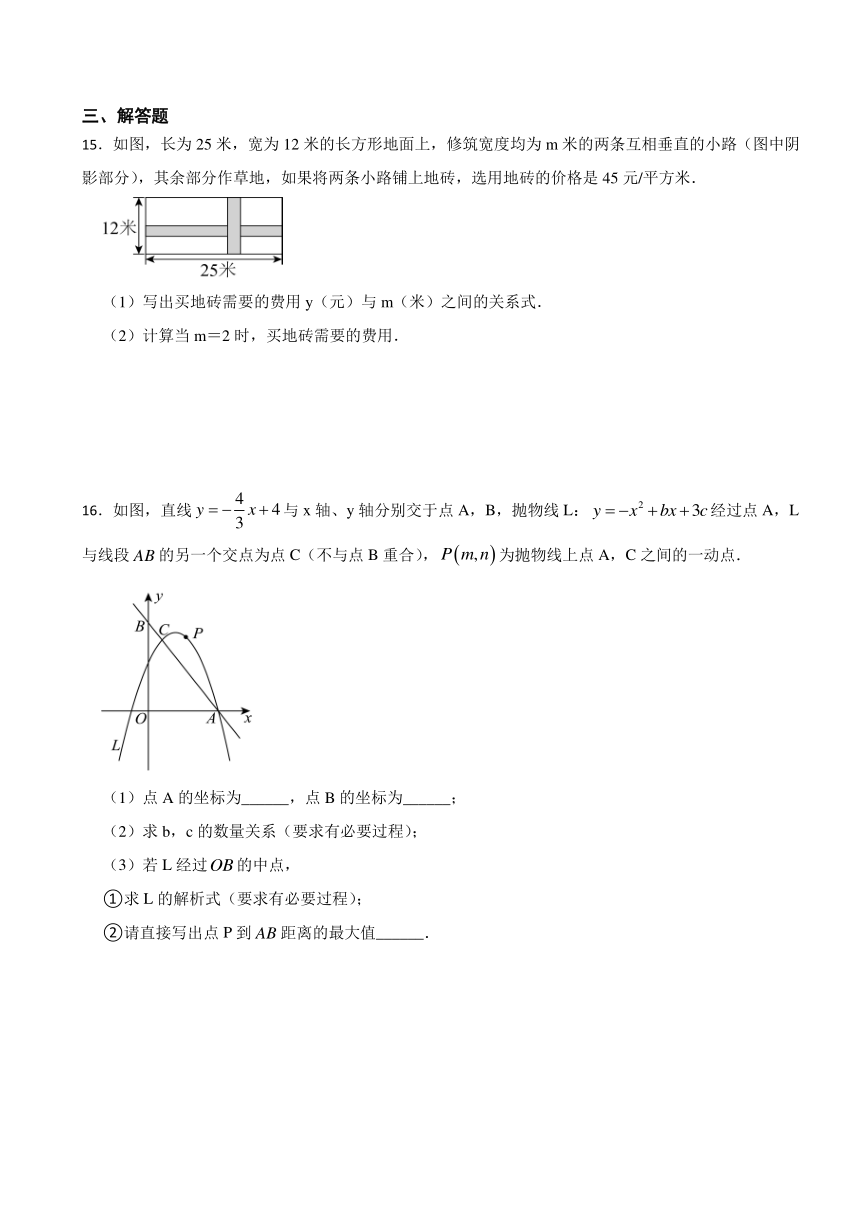
15.如图,长为25米,宽为12米的长方形地面上,修筑宽度均为m米的两条互相垂直的小路(图中阴影部分),其余部分作草地,如果将两条小路铺上地砖,选用地砖的价格是45元/平方米.
(1)写出买地砖需要的费用y(元)与m(米)之间的关系式.
(2)计算当m=2时,买地砖需要的费用.
16.如图,直线与x轴、y轴分别交于点A,B,抛物线L:经过点A,L与线段的另一个交点为点C(不与点B重合),为抛物线上点A,C之间的一动点.
(1)点A的坐标为______,点B的坐标为______;
(2)求b,c的数量关系(要求有必要过程);
(3)若L经过的中点,
①求L的解析式(要求有必要过程);
②请直接写出点P到距离的最大值______.
17.某超市销售一种进价为18元/千克的商品,经市场调查后发现,每天的销售量y(千克)与销售单价x(元/千克)有如下表所示的关系:
销售单价x(元/千克) --- 20 22.5 25 37.5 40 …
销售量y(千克) --- 30 27.5 25 12.5 10 …
(1)根据表中的数据在如图的坐标系中描点(x,y),并用平滑的线连结这些点,请用所学知识求出y关于x的函数表达式.
(2)设该超市每天销售这种商品的利润为w(元)(不计其他成本).
①求出w关于x的函数表达式,并求出获得最大利润时,销售单价为多少.
②超市本着“尽量让顾客享受实惠”的销售原则,求w=240元时的销售单价.
18.小张购进一批食材制作特色美食,每盒售价为50元,由于食材需要冷藏保存,导致成本逐日增加,第x天(且为整数)时每盒成本为p元,已知p与x之间满足一次函数关系;第3天时,每盒成本为21元;第7天时,每盒成本为25元,每天的销售量为y盒,y与x之间的关系如下表所示:
(1)求p与x的函数关系式;
(2)若每天的销售利润为w元,求w与x的函数关系式;
(3)请你帮小张求出第几天的销售利润最大,最大销售利润是多少元?
19.襄阳市某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种产品的成本为30元/件,且年销售量y(万件)关于售价x(元/件)的函数解析式为:
,
(1)若企业销售该产品获得自睥利润为W(万元),请直接写出年利润W(万元)关于售价(元/件)的函数解析式;
(2)当该产品的售价x(元/件)为多少时,企业销售该产品获得的年利润最大 最大年利润是多少
(3)若企业销售该产品的年利澜不少于750万元,试确定该产品的售价x(元/件)的取值范围.
20.某商品每件进价25元,在试销阶段该商品的日销售量y(件)与每件商品的日销售价x(元)之间的关系如图中的折线ABC所示(物价局规定,该商品每件的销售价不得低于进价且不得高于50元).
(1)直接写出y与x的函数关系式;
(2)若日销售单价x(元)为整数,则当日销售单价x(元)为多少时,该商品每天的销售利润最大?最大利润是多少;
(3)若该商品每天的销售利润不低于1200元,求销售单价x的取值范围.
21.清明是二十四节气之一,也是我国的传统节日,清明节吃青团是很多地方的习俗.清明节前市场上肉松蛋黄青团比芝麻青团的进价每盒便宜10元,某商家用800元购进的芝麻青团和用600元购进的肉松蛋黄青团盒数相同.在销售中,该商家发现芝麻青团每盒售价50元时,每天可售出100盒,当每盒售价提高1元时,每天少售出2盒.
(1)求芝麻青团和肉松蛋黄青团的进价;
(2)已知芝麻青团每盒的售价不高于65元,W表示该商家每天销售芝麻青团的利润(单位;元),芝麻青团每盒售价为多少元时,一天获得利润最大?最大利润是多少元?
22.如图所示,在平面直角坐标系xOy中,已知二次函数y=ax2+2ax+3的图象与x轴交于点A(-3,0),与y轴交于点B.
(1)求该函数的表达式及顶点坐标;
(2)点P(m,n)在该二次函数图象上,当m≤x≤m+3时,该二次函数有最大值2,请根据图象求出m的值;
(3)将该二次函数图象在点A,B之间的部分(含A,B两点)记为图象W.
①点Q在图象W上,连接QA,QB,求△ABQ面积的最大值;
②若直线y=c与图象W只有一个公共点,结合函数图象,直接写出c的取值范围.
答案解析部分
1.【答案】B
2.【答案】C
3.【答案】D
4.【答案】B
5.【答案】C
6.【答案】C
7.【答案】A
8.【答案】C
9.【答案】
10.【答案】6
11.【答案】
12.【答案】4
13.【答案】8
14.【答案】
15.【答案】(1)解:由题意得:两条小路的面积为:25m+12mm2=(37mm2)米2,
∴y=45×(37mm2)=1665m45m2;
(2)解:当m=2时,1665m45m2=1665×245×4=3150(元),
答:当m=2时,地砖的费用为3150元.
16.【答案】(1),
(2)解:将点代入抛物线L:,
得,,
∴,
∴;
故答案为:;
(3)解:∵,∴的中点,
①将、代入抛物线L:,
∴,
解得: ,
∴L的解析式为,
②
17.【答案】(1)解: 根据表中的数据在如图的坐标系中描点(x,y),并用平滑的线连结这些点 如下:
,
如图可知y关于x成一次函数关系,设y=kx+b(k≠0),将点(20,30)与(40,10)分别代入得,
解得,
∴y关于x的函数表达式为:y=-x+50;
(2)解:①由题意可得w=(x-18)(-x+50)=-x2+68x-900=-(x-34)2+256,
∵-1<0,
∴当x=34时,w最大,
∴超市每天销售这种商品获得最大利润时,销售单价为34元/千克;
②将w=240代入w=-(x-34)2+256得-(x-34)2+256=240,
解得x1=38,x2=30,
∵超市本着“尽量让顾客享受实惠”的销售原则,
∴x=30,
∴ w=240元时的销售单价为30元/千克.
18.【答案】(1)解:∵p与x之间满足一次函数关系,
∴可设p=kx+b(k≠0),
∵第3天时,每盒成本为21元;第7天时,每盒成本为25元,
∴当x=3时,y=21;当x=7时,y=25,
∴,
解得,
∴p与x的函数关系式为:p=x+18;
(2)解:当1≤x≤6时,w=10[50-(x+18)]=-10x+320,
当6<x≤15时,w=[50-(x+18)](x+6)=-x2+26x+192,
∴w与x的函数关系式为:;
(3)解:当1≤x≤6时,
∵-10<0,
∴w随x的增大而减小,
∴即当x=1时,w最大,最大利润为:-10+320=310,
当6<x≤15时,w=-x2+26x+192=-(x-13)2+361,
∴即当x=13时,w最大,最大利润为361,
综上所述,第13天时当天的销售利润最大,最大销售利润是361元.
19.【答案】(1)(2)当该产品的售价定为50元/件时,销售该产品的年利润最大,最大利润为800万元.(3)要使企业销售该产品的年利润不少于750万元,该产品的销售价x(元/件)的取值范围为45≤x≤55.
20.【答案】(1)解:.
(2)解:设销售利润为W元,则
①当时,,
∴时,元.
②当时,,
∵x为整数,
∴或43时,W取最大值,.
∵,
∴当日销售单价为42元或43元时,每天的销售利润最大,最大利润为1224元.
(3)解:由(2)知,当时,该商品每天的最大销售利润为1000元;
∴只有在时,每天的销售利润才可能不低于1200元;
∴,
∴,
∴.
21.【答案】(1)解:设芝麻青团的进价为每盒a元,则肉松蛋黄青团的进价为每盒(a﹣10)元,
根据题意得:,
解得a=40,
经检验,a=40是原方程的根,且符合题意.
此时a﹣10=40﹣10=30,
答:芝麻青团的进价为每盒40元,肉松蛋黄青团的进价为每盒30元.
(2)解:设芝麻青团每盒售价x元,
根据题意得:
,
∵a=﹣2<0,x≤65<70,
∴W随x的增大而增大,
∴当x=65时,W有最大值,最大值为1750,
∴芝麻青团每盒售价为65元时,一天获得利润最大,最大利润是1750元.
22.【答案】(1)解:把A(-3,0)代入y=ax2+2ax+3中,
得9a-6a+3=0,
解得a=-1,
∴抛物线的解析式为:y=-x2-2x+3,
∵y=-x2-2x+3=-(x+1)2+4,
∴抛物线的顶点坐标为(-1,4);
(2)解:当m+3<-1,即m<-4时,
∵m≤x≤m+3时,该二次函数有最大值2,
∴-(m+3)2-2(m+3)+3=2,
解得m=-4+ (舍)或m=-4- ,
当m>-1时,
∵m≤x≤m+3时,该二次函数有最大值2,
∴-m2-2m+3=2,
解得m=-1- (舍)或m=-1+ ,
故m的值为m==-4- 或m=-1+ ;
(3)解:①令x=0,得y=-x2-2x+3=3,
∴B(0,3),
设Q(t,-t2-2t+3)(-3≤t≤0),过Q作QM⊥y轴于点M,
则QM=-t,OM=-t2-2t+3,
∴△ABQ的面积S=S梯形OAQB-S△OAB-S△BQM
=
=
= (-3≤t≤0),
∴△ABQ面积的最大值为 ;
②由函数图象可知,当c=4或0≤c<3时,直线y=c与W只有一个交点,
∴c=4或0≤c<3.
一、单选题
1.在一个边长为2的正方形中挖去一个边长为x(0<x<2)的小正方形,如果设剩余部分的面积为y,那么y关于x的函数解析式是( )
A. B. C. D.
2.拱桥的形状是抛物线,其函数关系式为,当水面离桥顶的高度为m时,水面的宽度为( )米.
A.8 B.9 C.10 D.11
3.在羽毛球比赛中,某次羽毛球的运动路线呈抛物线形,羽毛球距地面的高度 与水平距离 之间的关系如图所示,点B为落地点,且 , ,羽毛球到达的最高点到y轴的距离为 ,那么羽毛球到达最高点时离地面的高度为( )
A. B. C. D.
4.如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )
A. B.
C. D.
5.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如表:下列结论错误的是( )
t 0 1 2 3 4 5 6 7 …
h 0 8 14 18 20 20 18 14 …
A.足球距离地面的最大高度超过20m
B.足球飞行路线的对称轴是直线
C.点(10,0)在该抛物线上
D.足球被踢出时,距离地面的高度逐渐下降.
6.如图,四边形中,,若,则四边形的面积最大值是( )
A.4 B.6 C.8 D.10
7.如图,是等腰直角三角形,,,点为边上一点,过点作,,垂足分别为,,点从点出发沿运动至点.设,,四边形的面积为,在运动过程中,下列说法正确的是( )
A.y与x满足一次函数关系,S与x满足二次函数关系,且S存在最大值
B.y与x满足一次函数关系,S与x满足二次函数关系,且S存在最小值
C.y与x满足反比例函数关系,S与x满足二次函数关系,且S存在最大值
D.y与x满足反比例函数关系,S与x满足二次函数关系,且S存在最小值
8.据省统计局公布的数据,合肥市2021年第一季度GDP总值约为2.4千亿元人民币,若我市第三季度GDP总值为y千亿元人民币,平均每个季度GDP增长的百分率为x,则y关于x的函数表达式是( )
A.y=2.4(1+2x) B.y=2.4(1-x)2
C.y=2.4(1+x)2 D.y=2.4+2.4(1+x)+2.4(1+x)2
二、填空题
9.原价为160元的电器连续两次降价后的价格为y元,若平均每次降价的百分率是x,则y与x的函数表达式为 .
10.一小球被抛出后,距离地面的高度h(米)和飞行时间t(秒)满足下面函数关系式,则小球距离地面的最大高度是 米.
11.在一个边长为2的正方形中挖去一个小正方形,使小正方形四周剩下部分的宽度均为x,若剩下阴影部分的面积为y,那么y关于x的函数解析式是 .
12.以40m/s的速度将小球沿与地面成30度角的方向击出时,球的飞行路线是一条抛物线.如果不考虑空气阻力,球的飞行高度h(单位m)与飞行时间t(单位s)之间具有函数关系:h=20t﹣5t2,那么球从飞出到落地要用的时间是 s.
13.如图,正方形 的边长为4, 、 、 、 分别是边 、 、 、 上的动点, .则四边形 面积的最小值为 .
14.如图,人工喷泉有一个竖直的喷水枪 ,喷水口A距地面 ,喷出水流的运动路线是抛物线,如果水流的最高点P到喷水枪 所在直线的距离为 ,且到地面的距离为 ,则水流的落地点C到水枪底部B的距离为 .
三、解答题
15.如图,长为25米,宽为12米的长方形地面上,修筑宽度均为m米的两条互相垂直的小路(图中阴影部分),其余部分作草地,如果将两条小路铺上地砖,选用地砖的价格是45元/平方米.
(1)写出买地砖需要的费用y(元)与m(米)之间的关系式.
(2)计算当m=2时,买地砖需要的费用.
16.如图,直线与x轴、y轴分别交于点A,B,抛物线L:经过点A,L与线段的另一个交点为点C(不与点B重合),为抛物线上点A,C之间的一动点.
(1)点A的坐标为______,点B的坐标为______;
(2)求b,c的数量关系(要求有必要过程);
(3)若L经过的中点,
①求L的解析式(要求有必要过程);
②请直接写出点P到距离的最大值______.
17.某超市销售一种进价为18元/千克的商品,经市场调查后发现,每天的销售量y(千克)与销售单价x(元/千克)有如下表所示的关系:
销售单价x(元/千克) --- 20 22.5 25 37.5 40 …
销售量y(千克) --- 30 27.5 25 12.5 10 …
(1)根据表中的数据在如图的坐标系中描点(x,y),并用平滑的线连结这些点,请用所学知识求出y关于x的函数表达式.
(2)设该超市每天销售这种商品的利润为w(元)(不计其他成本).
①求出w关于x的函数表达式,并求出获得最大利润时,销售单价为多少.
②超市本着“尽量让顾客享受实惠”的销售原则,求w=240元时的销售单价.
18.小张购进一批食材制作特色美食,每盒售价为50元,由于食材需要冷藏保存,导致成本逐日增加,第x天(且为整数)时每盒成本为p元,已知p与x之间满足一次函数关系;第3天时,每盒成本为21元;第7天时,每盒成本为25元,每天的销售量为y盒,y与x之间的关系如下表所示:
(1)求p与x的函数关系式;
(2)若每天的销售利润为w元,求w与x的函数关系式;
(3)请你帮小张求出第几天的销售利润最大,最大销售利润是多少元?
19.襄阳市某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种产品的成本为30元/件,且年销售量y(万件)关于售价x(元/件)的函数解析式为:
,
(1)若企业销售该产品获得自睥利润为W(万元),请直接写出年利润W(万元)关于售价(元/件)的函数解析式;
(2)当该产品的售价x(元/件)为多少时,企业销售该产品获得的年利润最大 最大年利润是多少
(3)若企业销售该产品的年利澜不少于750万元,试确定该产品的售价x(元/件)的取值范围.
20.某商品每件进价25元,在试销阶段该商品的日销售量y(件)与每件商品的日销售价x(元)之间的关系如图中的折线ABC所示(物价局规定,该商品每件的销售价不得低于进价且不得高于50元).
(1)直接写出y与x的函数关系式;
(2)若日销售单价x(元)为整数,则当日销售单价x(元)为多少时,该商品每天的销售利润最大?最大利润是多少;
(3)若该商品每天的销售利润不低于1200元,求销售单价x的取值范围.
21.清明是二十四节气之一,也是我国的传统节日,清明节吃青团是很多地方的习俗.清明节前市场上肉松蛋黄青团比芝麻青团的进价每盒便宜10元,某商家用800元购进的芝麻青团和用600元购进的肉松蛋黄青团盒数相同.在销售中,该商家发现芝麻青团每盒售价50元时,每天可售出100盒,当每盒售价提高1元时,每天少售出2盒.
(1)求芝麻青团和肉松蛋黄青团的进价;
(2)已知芝麻青团每盒的售价不高于65元,W表示该商家每天销售芝麻青团的利润(单位;元),芝麻青团每盒售价为多少元时,一天获得利润最大?最大利润是多少元?
22.如图所示,在平面直角坐标系xOy中,已知二次函数y=ax2+2ax+3的图象与x轴交于点A(-3,0),与y轴交于点B.
(1)求该函数的表达式及顶点坐标;
(2)点P(m,n)在该二次函数图象上,当m≤x≤m+3时,该二次函数有最大值2,请根据图象求出m的值;
(3)将该二次函数图象在点A,B之间的部分(含A,B两点)记为图象W.
①点Q在图象W上,连接QA,QB,求△ABQ面积的最大值;
②若直线y=c与图象W只有一个公共点,结合函数图象,直接写出c的取值范围.
答案解析部分
1.【答案】B
2.【答案】C
3.【答案】D
4.【答案】B
5.【答案】C
6.【答案】C
7.【答案】A
8.【答案】C
9.【答案】
10.【答案】6
11.【答案】
12.【答案】4
13.【答案】8
14.【答案】
15.【答案】(1)解:由题意得:两条小路的面积为:25m+12mm2=(37mm2)米2,
∴y=45×(37mm2)=1665m45m2;
(2)解:当m=2时,1665m45m2=1665×245×4=3150(元),
答:当m=2时,地砖的费用为3150元.
16.【答案】(1),
(2)解:将点代入抛物线L:,
得,,
∴,
∴;
故答案为:;
(3)解:∵,∴的中点,
①将、代入抛物线L:,
∴,
解得: ,
∴L的解析式为,
②
17.【答案】(1)解: 根据表中的数据在如图的坐标系中描点(x,y),并用平滑的线连结这些点 如下:
,
如图可知y关于x成一次函数关系,设y=kx+b(k≠0),将点(20,30)与(40,10)分别代入得,
解得,
∴y关于x的函数表达式为:y=-x+50;
(2)解:①由题意可得w=(x-18)(-x+50)=-x2+68x-900=-(x-34)2+256,
∵-1<0,
∴当x=34时,w最大,
∴超市每天销售这种商品获得最大利润时,销售单价为34元/千克;
②将w=240代入w=-(x-34)2+256得-(x-34)2+256=240,
解得x1=38,x2=30,
∵超市本着“尽量让顾客享受实惠”的销售原则,
∴x=30,
∴ w=240元时的销售单价为30元/千克.
18.【答案】(1)解:∵p与x之间满足一次函数关系,
∴可设p=kx+b(k≠0),
∵第3天时,每盒成本为21元;第7天时,每盒成本为25元,
∴当x=3时,y=21;当x=7时,y=25,
∴,
解得,
∴p与x的函数关系式为:p=x+18;
(2)解:当1≤x≤6时,w=10[50-(x+18)]=-10x+320,
当6<x≤15时,w=[50-(x+18)](x+6)=-x2+26x+192,
∴w与x的函数关系式为:;
(3)解:当1≤x≤6时,
∵-10<0,
∴w随x的增大而减小,
∴即当x=1时,w最大,最大利润为:-10+320=310,
当6<x≤15时,w=-x2+26x+192=-(x-13)2+361,
∴即当x=13时,w最大,最大利润为361,
综上所述,第13天时当天的销售利润最大,最大销售利润是361元.
19.【答案】(1)(2)当该产品的售价定为50元/件时,销售该产品的年利润最大,最大利润为800万元.(3)要使企业销售该产品的年利润不少于750万元,该产品的销售价x(元/件)的取值范围为45≤x≤55.
20.【答案】(1)解:.
(2)解:设销售利润为W元,则
①当时,,
∴时,元.
②当时,,
∵x为整数,
∴或43时,W取最大值,.
∵,
∴当日销售单价为42元或43元时,每天的销售利润最大,最大利润为1224元.
(3)解:由(2)知,当时,该商品每天的最大销售利润为1000元;
∴只有在时,每天的销售利润才可能不低于1200元;
∴,
∴,
∴.
21.【答案】(1)解:设芝麻青团的进价为每盒a元,则肉松蛋黄青团的进价为每盒(a﹣10)元,
根据题意得:,
解得a=40,
经检验,a=40是原方程的根,且符合题意.
此时a﹣10=40﹣10=30,
答:芝麻青团的进价为每盒40元,肉松蛋黄青团的进价为每盒30元.
(2)解:设芝麻青团每盒售价x元,
根据题意得:
,
∵a=﹣2<0,x≤65<70,
∴W随x的增大而增大,
∴当x=65时,W有最大值,最大值为1750,
∴芝麻青团每盒售价为65元时,一天获得利润最大,最大利润是1750元.
22.【答案】(1)解:把A(-3,0)代入y=ax2+2ax+3中,
得9a-6a+3=0,
解得a=-1,
∴抛物线的解析式为:y=-x2-2x+3,
∵y=-x2-2x+3=-(x+1)2+4,
∴抛物线的顶点坐标为(-1,4);
(2)解:当m+3<-1,即m<-4时,
∵m≤x≤m+3时,该二次函数有最大值2,
∴-(m+3)2-2(m+3)+3=2,
解得m=-4+ (舍)或m=-4- ,
当m>-1时,
∵m≤x≤m+3时,该二次函数有最大值2,
∴-m2-2m+3=2,
解得m=-1- (舍)或m=-1+ ,
故m的值为m==-4- 或m=-1+ ;
(3)解:①令x=0,得y=-x2-2x+3=3,
∴B(0,3),
设Q(t,-t2-2t+3)(-3≤t≤0),过Q作QM⊥y轴于点M,
则QM=-t,OM=-t2-2t+3,
∴△ABQ的面积S=S梯形OAQB-S△OAB-S△BQM
=
=
= (-3≤t≤0),
∴△ABQ面积的最大值为 ;
②由函数图象可知,当c=4或0≤c<3时,直线y=c与W只有一个交点,
∴c=4或0≤c<3.
同课章节目录
