2.2 平行四边形 课件

课件26张PPT。§2.2.1平行四边形的性质(1) 2.2平行四边形看一看：下面的图片中，有哪些你熟悉的哪些图形？学习目标
1、在对平行四边形认识的基础上，探索并掌握平行四边形的性质。
2、会利用平行四边形的性质去解决实际问题。
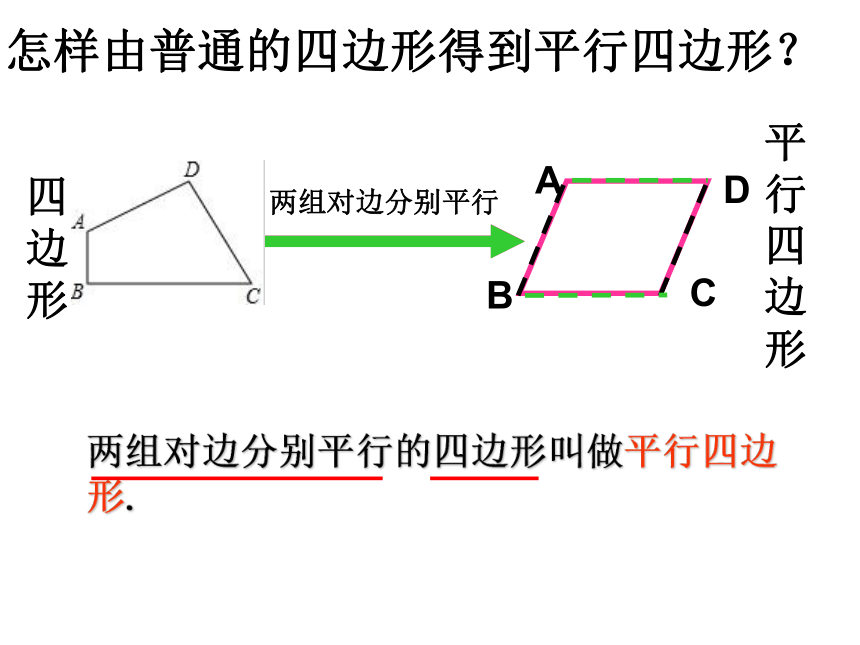
看一看：下面的图片中，有你熟悉的哪些图形？你是怎么定义的？两组对边分别平行四边形平行四边形两组对边分别平行的四边形叫做平行四边形.怎样由普通的四边形得到平行四边形？
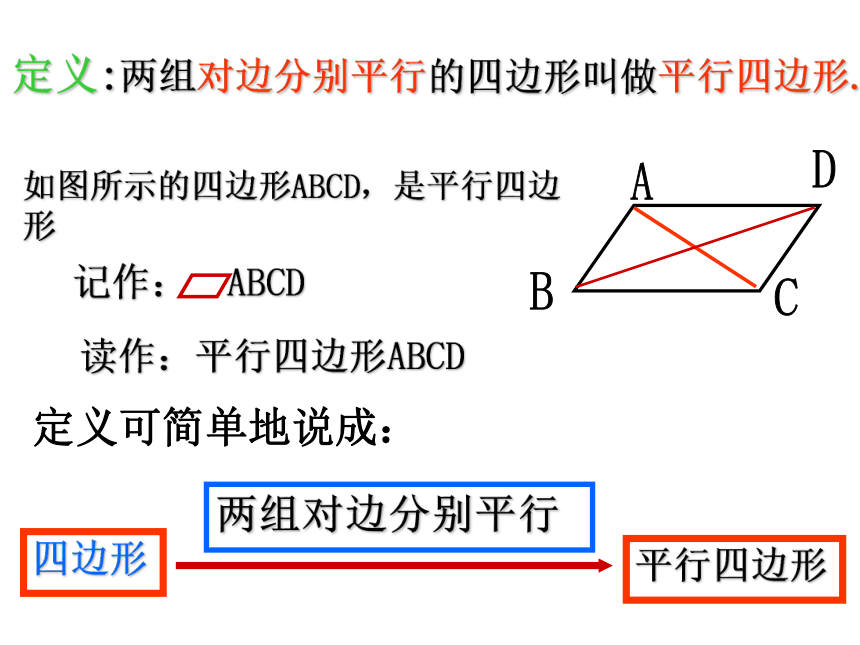
定义:两组对边分别平行的四边形叫做平行四边形. 如图所示的四边形ABCD，是平行四边形记作： ABCD读作：平行四边形ABCD四边形平行四边形两组对边分别平行定义可简单地说成：∵　四边形ABCD是平行四边形
∴　AB∥CD
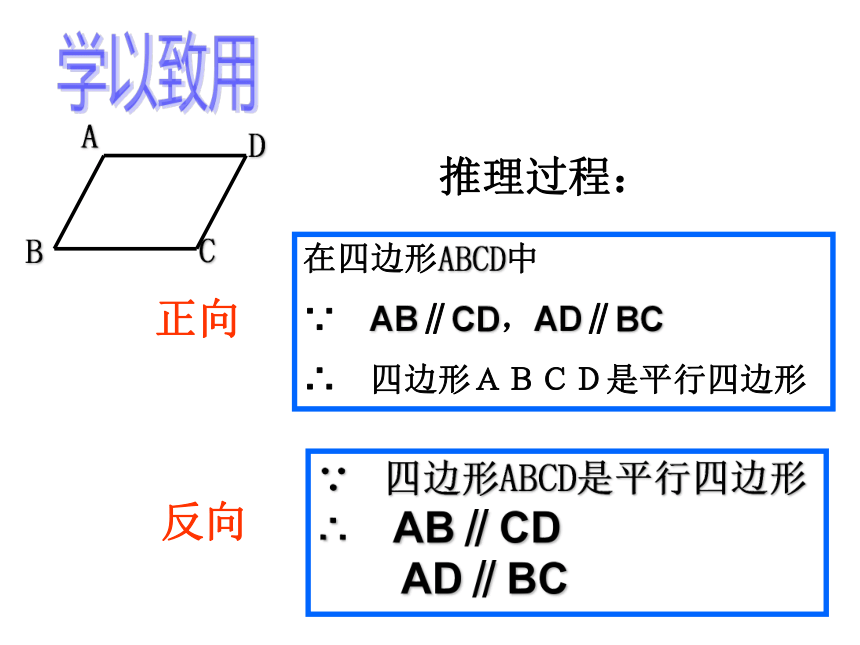
　　 AD∥BC在四边形ABCD中
∵　AB∥CD，AD∥BC
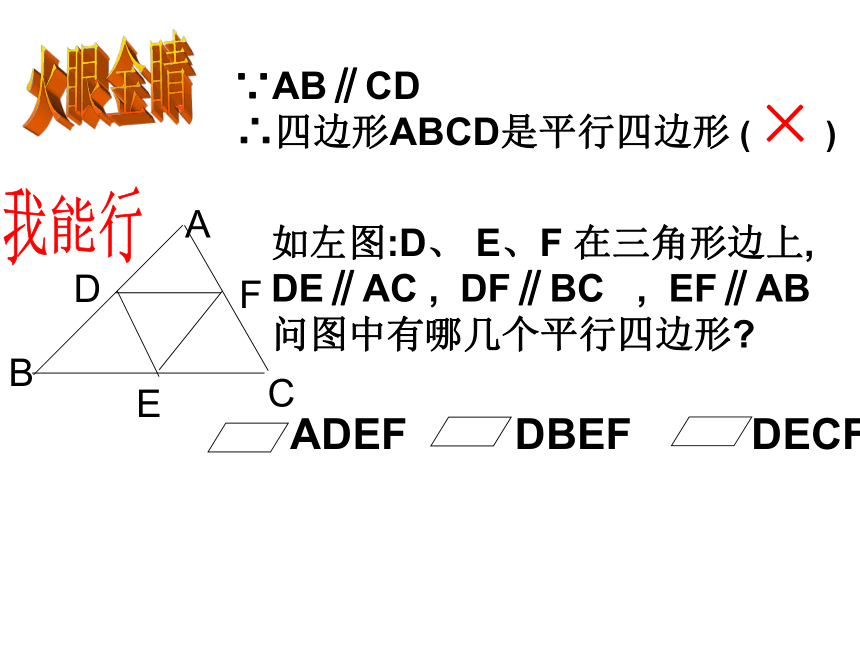
∴　四边形ＡＢＣＤ是平行四边形　　　　　　推理过程：正向反向学以致用 ∵AB∥CD
∴四边形ABCD是平行四边形 ( ) ×火眼金睛 (1)根据定义画一个平行四边形.
(2)观察这个平行四边形，除了“两组对边分别平行”以外，你还发现了什么？

(3)你有方法来验证猜想吗？探究一：平行四边形除两组对边分别平行外,你还能得到对边有什么关系?
用什么方法得到这个关系? 思考与讨论边的关系BADc方法一 观察、度量D方法二 剪开、叠合 C点拨：先根据题目画图，
再写“已知”与 “求证”，最后证明。 已知:四边形ABCD是平行四边形
求证:AD=BC, AB=DC 解法二: 连接BD平行四边形的对边平行且相等这个性质用几何语言如何表示？平行四边形的性质 1分析：要证的是不在同一个三角形的边相等,可作辅助线,转化为三角形的全等问题解决 ∵ ∴ 转化思想方法一 观察、度量方法二 剪开、叠合 ( Flash动画演示)证明：
∵四边形ABCD是平行四边形 ∴AB∥CD，AD∥BC
∴∠A+∠B=180 ∠A+∠D=180
∴∠B=∠D（同角的补角相等）
同理可得∠A=∠C方法三 证明 平行四边形的性质 2平行四边形的对角相等平行四边形的邻角互补平行四边形的对边平行且相等
平行四边形的对角相等平行四边形的邻角互补平行四边形的性质ABCD 例题教学： ? 例： 如图，小明用一根36m长的绳子围成了一个平行四边形的场地，其中一条边AB长为8m，其他三条边的长各是多少？解： ∵四边形ABCD是平行四边形∵ AB=8 有一块形状如图 所示的玻璃，不小心把EDF部分打碎了，现在只测得AE=60cm、BC=80cm，∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗？实际问题尝试应用方程思想 ABCD 的周长是20cm, AB与BC的差为2cm,求平行四边形各边的长。
真高兴动脑筋如图L１∥L２，
　　ＡＢ∥ＣＤ那么ＡＢ与ＣＤ是否相等？为什么？结论：夹在两条平行线间的平行线段相等4030120°120°60°120°40°随堂练习? ：3：如图，平行四边形ABCD中，AE⊥BD，CF⊥BD，垂足分别为E、F.
求证：∠BAE＝∠DCF。 感悟与收获通过本节课的学习，你有什么收获？平行四边形的邻角互补
2、平行四边形的性质:1 、平行四边形的定义:两组对边分别平行的四边形叫做平行四边形平行四边形的对边平行且相等
平行四边形的对角相等 1、下列性质中,平行四边形不一定具有的是( )
A对角相等 B对角互补
C邻角互补 D内角和是360。B9100o80o验收反馈4、一个平行四边形相邻两边的比是 2 : 3, 其周长是40,求
它的各边长。 解: 设BC=2x, AB=3x
由题意得 (2x+3x )×2=40
解得x = 4 ∴2x = 8 3x = 12
那么这个平行四边形的各边长为8 、 12 、 8 、 12作业：
(1)必做题：课本42页 练习：1、2
（2）课后:预习平行四边形的对角线的特点同学们，再见！