2.2平行四边形 课件

课件21张PPT。平行四边形的性质（一）下面的图片中，有你熟悉的哪些图形？
学习目标:(1)理解平行四边形的有关概念。
(2)经历平行四边形性质的探索过程，并掌握平行四边形的性质。
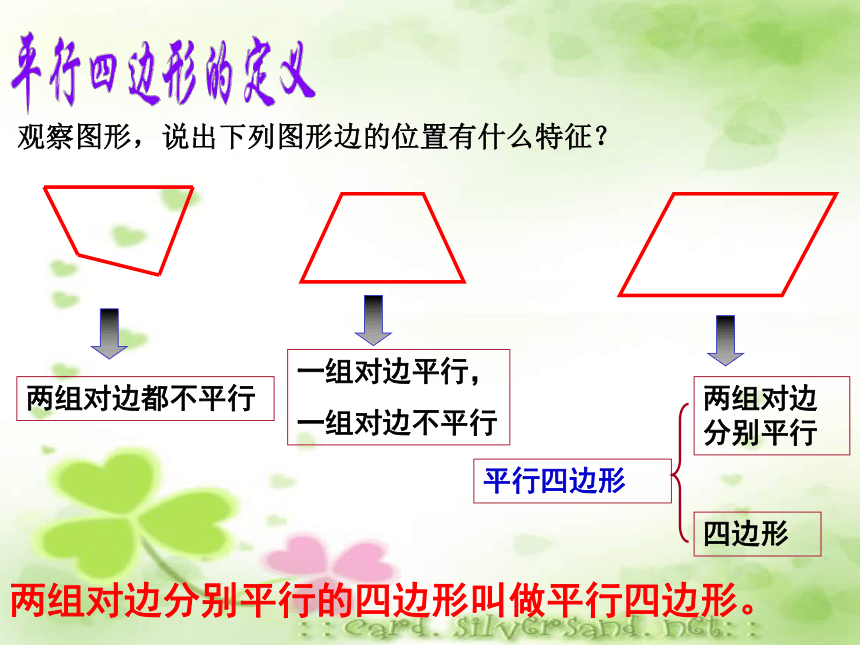
(3)能运用平行四边形的性质进行推理与计算。两组对边都不平行一组对边平行，
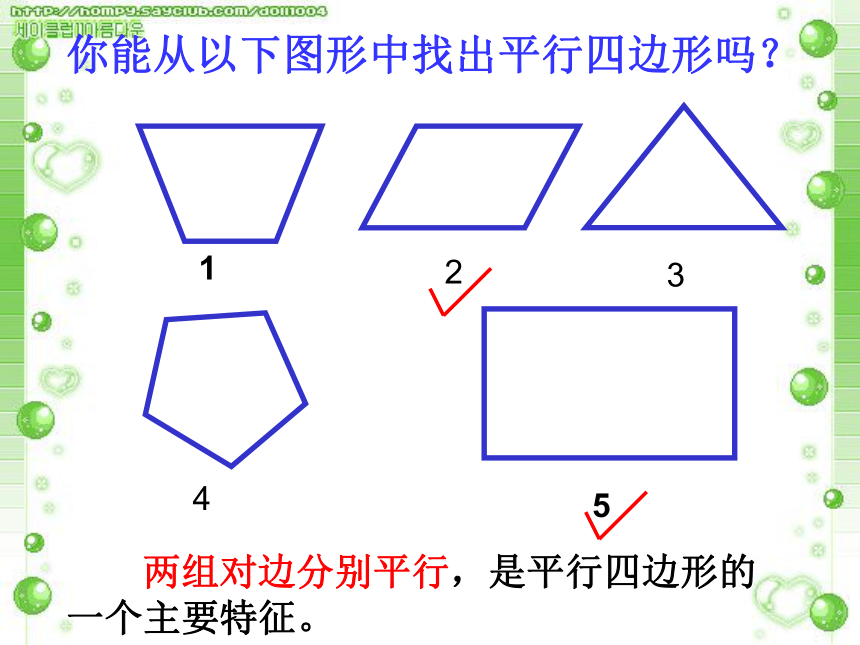
一组对边不平行两组对边分别平行四边形平行四边形两组对边分别平行的四边形叫做平行四边形。观察图形，说出下列图形边的位置有什么特征？你能从以下图形中找出平行四边形吗？ 两组对边分别平行，是平行四边形的一个主要特征。23145平行四边形相对的边称为 对边 相邻的边称为邻边
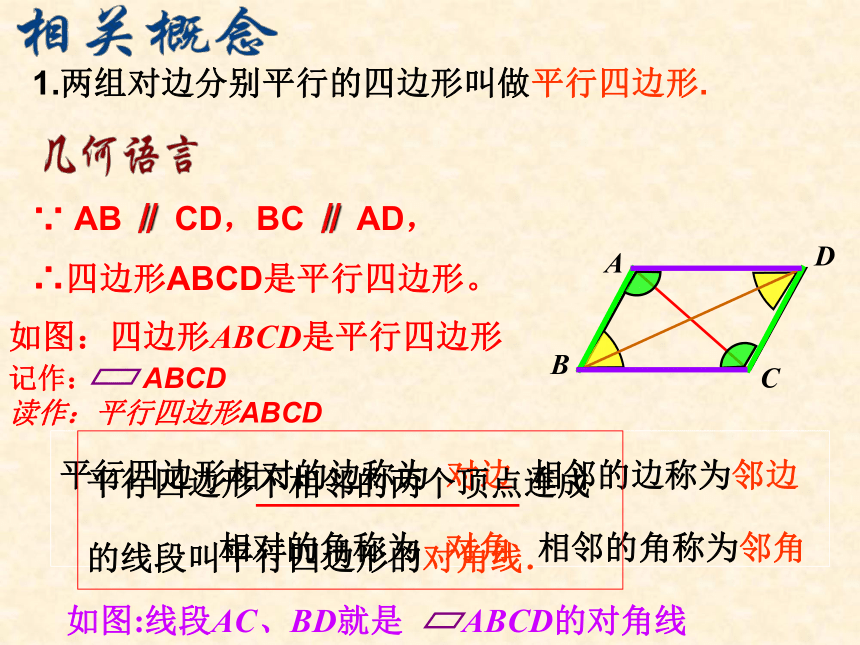
相对的角称为 对角 相邻的角称为邻角1.两组对边分别平行的四边形叫做平行四边形.∵ AB ∥ CD，BC ∥ AD，
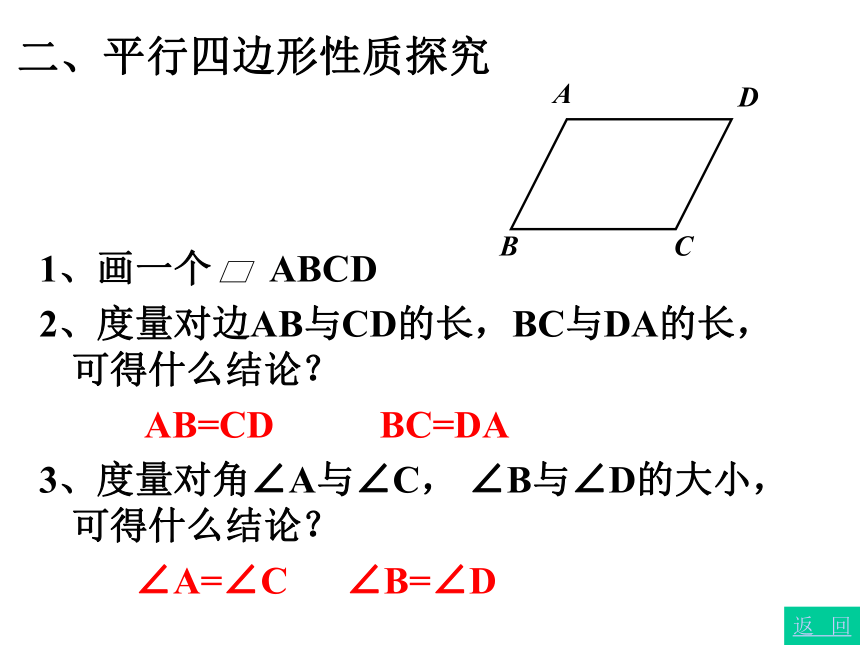
∴四边形ABCD是平行四边形。二、平行四边形性质探究1、画一个 ABCD
2、度量对边AB与CD的长，BC与DA的长，可得什么结论？
AB=CD BC=DA
3、度量对角∠A与∠C， ∠B与∠D的大小，可得什么结论？
∠A=∠C ∠B=∠D返回上列结论一定成立吗？怎样证明？4、已知：如图，在 ABCD中
求证：AB=CD，BC=DA，
∠A=∠C，∠B=∠D.
证明：连接AC∵ 四边形ABCD是平行四边形，
∴ AD∥BC、AB∥CD∴∠1=∠2，∠3=∠4
∵AC=AC∴⊿ABC≌⊿CDA∴AD=BC，AB=CD，∠B=∠D
又∵∠1=∠2，∠3 =∠4
∴ ∠1+∠3= ∠2 +∠4
即∠BAD=∠BCD
返回平行四边形的对边平行且相等，对角相等。几何叙述：
∵四边形ABCD是平行四边形
∴ AB ∥ CD， BC ∥ AD
AB=CD， BC=AD.
∠A=∠C， ∠B=∠D。
1.如图，在 ABCD 中，已知A=40°，求其它三个内角的度数。体会 应用3.已知平行四边形的周长为34cm，两邻边之差是3cm，则两邻边的长分别为： 。4.已知平行四边形ABCD中，∠A: ∠ B: ∠ C: ∠ D的值可以是（ )
A 1:2:3:4 B 2:3:3:2 C 2:3:2:3 D 2:2:3:3体会 应用 5、P42 T1、2 四边形ABCD和BCEF均为平行四边形，AD=2cm ，∠A=65 °，∠E=33 °，
求EF和 ∠BGC.
例
题
GBCFEAD12 如图，四边形ABCD是平行四边形，
E是AD边上的中点，连接CE交BA的延长线于点F.证明：AF=AB 如图，直线L1与L2平行，AB、CD是L1与L2
之间的任意两条平行线段。试问：AB与CD是否相等？为什么？合作探究 如图，直线L1与L2平行，那么△ABC和△ ACD
的面积是相等的。你能说出理由吗？你还能在这两条平行线L1, L2之间画出其他与△ ABC面积相等的三角形吗?练习检测： 1、P42 T2练习检测：2、P49 T1（★）学校买了四棵树，准备栽在花园里，已经栽了三棵（如图），现在学校希望这四棵树能组成一个平行四边形，你觉得第四棵树应该栽在哪里？A1A3A2能力提升本节课你有
什么收获？回味无穷:课作：P49 T3
家作：学法大视野P16-17

作业: