湘教版八年级上册数学期中综合模拟测试卷(含答案)
文档属性
| 名称 | 湘教版八年级上册数学期中综合模拟测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 652.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-18 00:00:00 | ||
图片预览




文档简介
期中综合测试卷
时间:120分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(本大题共12小题,每小题3分,共36分)
1. 已知三角形的两边长分别为1和4,第三边长为整数,则该三角形的周长为( )
A. 7 B. 8 C. 9 D. 10
2. 下列各分式中,最简分式是 ( )
3.如图,Rt△ABC中,∠C=90°,∠B=30°,分别以点A和点B为圆心,大于 的长为半径作弧,两弧相交于M,N两点,作直线MN,交 BC于点D,连接AD,则∠CAD 的度数是
( )
A. 20° B. 30° C. 45° D. 60°
解分式方程:
解:x-(3-x)=x-2……①
x--3 +x=x-2……②
x+x-x= -2+3……③
x=1…………………④
经检验:x=1是原方程的解.
第4题图
4. 如图,在框中解分式方程的4个步骤中,依据等式基本性质的是 ( )
A.①② B.②④ C.①③ D.③④
5. 图中的小正方形边长相等,若△MNP≌△MFQ,则点Q可能是图中的 ( )
A. 点 D B. 点 C C. 点 B D. 点 A
6. 判断命题“如果n<1,那么 是假命题,只需举出一个反例.反例中的n可以为 ( )
A. -2 C. 0 D
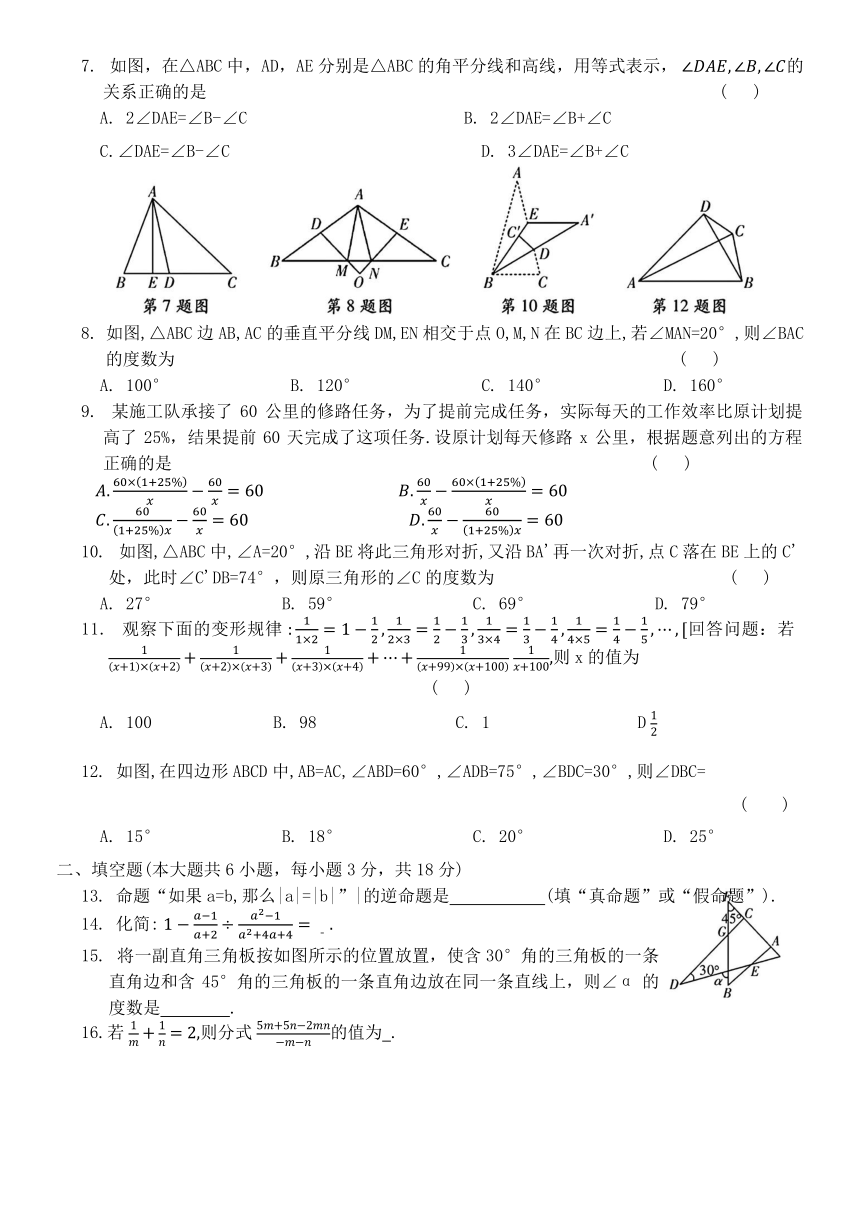
7. 如图,在△ABC中,AD,AE分别是△ABC的角平分线和高线,用等式表示, 的关系正确的是 ( )
A. 2∠DAE=∠B-∠C B. 2∠DAE=∠B+∠C
C.∠DAE=∠B-∠C D. 3∠DAE=∠B+∠C
8. 如图,△ABC边AB,AC的垂直平分线DM,EN相交于点O,M,N在BC边上,若∠MAN=20°,则∠BAC的度数为 ( )
A. 100° B. 120° C. 140° D. 160°
9. 某施工队承接了60公里的修路任务,为了提前完成任务,实际每天的工作效率比原计划提高了25%,结果提前60天完成了这项任务.设原计划每天修路x公里,根据题意列出的方程正确的是 ( )
10. 如图,△ABC中,∠A=20°,沿BE将此三角形对折,又沿BA'再一次对折,点C落在BE上的C'处,此时∠C'DB=74°,则原三角形的∠C的度数为 ( )
A. 27° B. 59° C. 69° D. 79°
11. 观察下面的变形规律 回答问题:若 则x的值为 ( )
A. 100 B. 98 C. 1 D
12. 如图,在四边形ABCD中,AB=AC,∠ABD=60°,∠ADB=75°,∠BDC=30°,则∠DBC=
( )
A. 15° B. 18° C. 20° D. 25°
二、填空题(本大题共6小题,每小题3分,共18分)
13. 命题“如果a=b,那么|a|=|b|”|的逆命题是 (填“真命题”或“假命题”).
14. 化简:
15. 将一副直角三角板按如图所示的位置放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上,则∠α的度数是 .
16.若 则分式 的值为 .
17. 如图,在 中, ,三角形的外角. 和 的平分线交于点E,则. °.
18. 如图,在△ABC 与△AEF 中,AB =AE,BC=EF,∠B =∠E,AB 交EF 于点D,给出下列结论:①∠AFC=∠C;②DF=CF;③BC=DE+DF;④∠BFD=∠CAF.其中正确的结论是 .(填序号)
三、解答题(共66分)
19. (6分)(遵义中考)化简式子 并在-2,-1,0,1,2中选取一个合适的数作为a的值代入求值.
20. (6分)如图,在 中,AD是BC边上的中线,E是AB边上一点,过点C作CF 交ED的延长线于点 F.
(1)求证:
(2)当 时,求AC的长.
21. (6分)小明解答“先化简,再求值: 其中 的过程如图.请指出解答过程中错误步骤的序号,并写出正确的解答过程.
解:
…………………………………②
……………………………………③
当 时,原式
……… ·④
……………⑤
22. (8分)如图,在四边形ABCD中, 过B作 ,垂足为点E,过点A作 BE,垂足为点 F,且
(1)求证:.
(2)连接BD,且BD平分. 交AF于点G.求证: 是等腰三角形.
23. (8分)数学课堂上,老师提出问题:可以通过通分将两个分式的和表示成一个分式的形式,是否也可以将一个分式 表示成两个分式和的形式 其中这两个分式的分母分别为x+1和x-1.小明通过观察、思考,发现可以用待定系数法解决上面问题.具体过程如下:设
则有
故有 解得
所以
问题解决:
(1)设 求A,B的值.
(2)直接写出方程 的解.
24. (10分)已知,如图, 中, 于 D,BE平分 且 于E,与CD 相交于点F,H是BC边的中点,连接 DH 与BE相交于点 G.
(1)求证:
(2)求证:
(3)比较CE 与 BG的大小并说明理由.
25. (10分)为励行节能减排,倡导绿色出行,去年以来“共享单车”公益活动登陆某市中心城区.某公司拟在甲、乙两个街道社区投放一批“共享单车”,这批自行车包括A,B两种不同的款型.请回答下列问题:
问题1:单价
该公司早期在甲街区进行了试点投放,共投放A,B两型自行车各50辆,投放成本共计7500元,其中 B型车的成本单价比A型车高10元,A,B两型自行车的单价各是多少元
问题2:投放方式
该公司决定采取如下投放方式:甲街区每1000人投放a辆“共享单车”,乙街区每1000人投放 辆“共享单车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1 200辆,如果两个街区共有15万人,试求a的值.
26. (12分)(1)如图①,在正方形ABCD中,M是BC边(不含端点B,C)上任意一点,P是BC延长线上一点,N是 的平分线上一点.若 求证:
下面给出一种证明的思路.
证明:在边AB上截取 ,连接ME.在正方形ABCD 中,. BC. AE.
下面请你完成余下的证明过程.
(2)若将(1)中的“正方形ABCD”改为“正三角形 (如图②),N是. 的平分线上一点,则当 时,结论 是否还成立 请说明理由.
期中综合测试卷
1. C2. C 3. B 4. C 5. A 6. A 7. A8. A 9. D 10. D11. B 12. A
13. 假命题 15. 75° 16. -4 17. 66.5 18.①③④
19. 解:原式
当 时,原式 =
20. (1)证明:
∵ AD 是 BC边上的中线,
(2)解:
21. 解:步骤①、②有误,
原式
当 时,
原式
22. 证明:(1)∵BE⊥CD,AF⊥BE,
∴∠AFB=∠BEC=90°,∴∠ABE+∠BAF=90°.
∵∠ABC=90°,∴∠ABE+∠EBC=90°,
∴∠BAF=∠EBC.
在△ABF和△BCE中,
∴ △ABF≌△BCE(ASA).
(2)∵∠ABC=90°,∴∠ABD+∠DBC=90°.
∵∠BED=90°,∴∠DBE+∠BDE=90°,
∵BD平分∠ABE,∴∠ABD=∠DBE.
∴∠DBC=∠BDE.∴BC=CD,即△BCD是等腰三角形.
23. 解: 解得
(2) 由 ( 1 ) 可 得
同 理 可 得
所以原方程可变形为: 解得 经检验, 是原方程的解,所以原方程的解为
24. (1)证明:
又 在△BFD和△CAD中,
∴△BFD≌△CAD(AAS),∴BF=AC.
(2)证明:∵ BE平分∠ABC,∴∠ABE=∠CBE.
在△ABE和△CBE中,
∴△ABE≌△CBE(ASA),∴CE=AE,
又
(3)解:CE∵ BD=CD,H为BC的中点,
∴DH⊥BC,BH=CH,
∴DH 为BC的垂直平分线,∴BG=CG.在 Rt△CEG中,CE25. 解:问题1:设A型车的成本单价为x元,则B型车的成本单价为(x+
10)元,依题意,得50x+50(x+10)=7500,
解得x=70,∴x+10=80,
答:A,B两型自行车的单价分别是70元和80元.
问题2:
由题可得
解得a=15.经检验,a=15是所列方程的解,且符合题意,故a的值为15.
26. (1)证明:∵AE=MC,
∴BE=BM,∴∠BEM=∠EMB =45°,
∴∠AEM=135°.∵CN平分∠DCP,∴∠PCN=45°,
∴∠MCN=135°.∴∠AEM =∠MCN.
在△AEM和△MCN中,
∴△AEM≌△MCN(ASA),∴AM=MN.
(2)解:仍然成立.理由:如图,在边AB上截取AE=MC,连接ME.
∵ △ABC是等边三角形,
∴AB=BC,∠B=∠ACB=60°,
∴∠ACP=120°.
∵AE=MC,∴BE=BM,∴∠BEM=∠EMB=60°,
∴∠AEM=120°.
∵CN平分∠ACP,∴∠PCN=60°,
∴∠MCN=120°.∴∠AEM=∠MCN.
∵ ∠CMN=180°-∠AMN-∠AMB=180°-∠B --∠AMB
=∠BAM,∴∠CMN=∠EAM.
在△AEM 和△MCN中, ∴△AEM≌△MCN(ASA),∴AM=MN.
时间:120分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(本大题共12小题,每小题3分,共36分)
1. 已知三角形的两边长分别为1和4,第三边长为整数,则该三角形的周长为( )
A. 7 B. 8 C. 9 D. 10
2. 下列各分式中,最简分式是 ( )
3.如图,Rt△ABC中,∠C=90°,∠B=30°,分别以点A和点B为圆心,大于 的长为半径作弧,两弧相交于M,N两点,作直线MN,交 BC于点D,连接AD,则∠CAD 的度数是
( )
A. 20° B. 30° C. 45° D. 60°
解分式方程:
解:x-(3-x)=x-2……①
x--3 +x=x-2……②
x+x-x= -2+3……③
x=1…………………④
经检验:x=1是原方程的解.
第4题图
4. 如图,在框中解分式方程的4个步骤中,依据等式基本性质的是 ( )
A.①② B.②④ C.①③ D.③④
5. 图中的小正方形边长相等,若△MNP≌△MFQ,则点Q可能是图中的 ( )
A. 点 D B. 点 C C. 点 B D. 点 A
6. 判断命题“如果n<1,那么 是假命题,只需举出一个反例.反例中的n可以为 ( )
A. -2 C. 0 D
7. 如图,在△ABC中,AD,AE分别是△ABC的角平分线和高线,用等式表示, 的关系正确的是 ( )
A. 2∠DAE=∠B-∠C B. 2∠DAE=∠B+∠C
C.∠DAE=∠B-∠C D. 3∠DAE=∠B+∠C
8. 如图,△ABC边AB,AC的垂直平分线DM,EN相交于点O,M,N在BC边上,若∠MAN=20°,则∠BAC的度数为 ( )
A. 100° B. 120° C. 140° D. 160°
9. 某施工队承接了60公里的修路任务,为了提前完成任务,实际每天的工作效率比原计划提高了25%,结果提前60天完成了这项任务.设原计划每天修路x公里,根据题意列出的方程正确的是 ( )
10. 如图,△ABC中,∠A=20°,沿BE将此三角形对折,又沿BA'再一次对折,点C落在BE上的C'处,此时∠C'DB=74°,则原三角形的∠C的度数为 ( )
A. 27° B. 59° C. 69° D. 79°
11. 观察下面的变形规律 回答问题:若 则x的值为 ( )
A. 100 B. 98 C. 1 D
12. 如图,在四边形ABCD中,AB=AC,∠ABD=60°,∠ADB=75°,∠BDC=30°,则∠DBC=
( )
A. 15° B. 18° C. 20° D. 25°
二、填空题(本大题共6小题,每小题3分,共18分)
13. 命题“如果a=b,那么|a|=|b|”|的逆命题是 (填“真命题”或“假命题”).
14. 化简:
15. 将一副直角三角板按如图所示的位置放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上,则∠α的度数是 .
16.若 则分式 的值为 .
17. 如图,在 中, ,三角形的外角. 和 的平分线交于点E,则. °.
18. 如图,在△ABC 与△AEF 中,AB =AE,BC=EF,∠B =∠E,AB 交EF 于点D,给出下列结论:①∠AFC=∠C;②DF=CF;③BC=DE+DF;④∠BFD=∠CAF.其中正确的结论是 .(填序号)
三、解答题(共66分)
19. (6分)(遵义中考)化简式子 并在-2,-1,0,1,2中选取一个合适的数作为a的值代入求值.
20. (6分)如图,在 中,AD是BC边上的中线,E是AB边上一点,过点C作CF 交ED的延长线于点 F.
(1)求证:
(2)当 时,求AC的长.
21. (6分)小明解答“先化简,再求值: 其中 的过程如图.请指出解答过程中错误步骤的序号,并写出正确的解答过程.
解:
…………………………………②
……………………………………③
当 时,原式
……… ·④
……………⑤
22. (8分)如图,在四边形ABCD中, 过B作 ,垂足为点E,过点A作 BE,垂足为点 F,且
(1)求证:.
(2)连接BD,且BD平分. 交AF于点G.求证: 是等腰三角形.
23. (8分)数学课堂上,老师提出问题:可以通过通分将两个分式的和表示成一个分式的形式,是否也可以将一个分式 表示成两个分式和的形式 其中这两个分式的分母分别为x+1和x-1.小明通过观察、思考,发现可以用待定系数法解决上面问题.具体过程如下:设
则有
故有 解得
所以
问题解决:
(1)设 求A,B的值.
(2)直接写出方程 的解.
24. (10分)已知,如图, 中, 于 D,BE平分 且 于E,与CD 相交于点F,H是BC边的中点,连接 DH 与BE相交于点 G.
(1)求证:
(2)求证:
(3)比较CE 与 BG的大小并说明理由.
25. (10分)为励行节能减排,倡导绿色出行,去年以来“共享单车”公益活动登陆某市中心城区.某公司拟在甲、乙两个街道社区投放一批“共享单车”,这批自行车包括A,B两种不同的款型.请回答下列问题:
问题1:单价
该公司早期在甲街区进行了试点投放,共投放A,B两型自行车各50辆,投放成本共计7500元,其中 B型车的成本单价比A型车高10元,A,B两型自行车的单价各是多少元
问题2:投放方式
该公司决定采取如下投放方式:甲街区每1000人投放a辆“共享单车”,乙街区每1000人投放 辆“共享单车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1 200辆,如果两个街区共有15万人,试求a的值.
26. (12分)(1)如图①,在正方形ABCD中,M是BC边(不含端点B,C)上任意一点,P是BC延长线上一点,N是 的平分线上一点.若 求证:
下面给出一种证明的思路.
证明:在边AB上截取 ,连接ME.在正方形ABCD 中,. BC. AE.
下面请你完成余下的证明过程.
(2)若将(1)中的“正方形ABCD”改为“正三角形 (如图②),N是. 的平分线上一点,则当 时,结论 是否还成立 请说明理由.
期中综合测试卷
1. C2. C 3. B 4. C 5. A 6. A 7. A8. A 9. D 10. D11. B 12. A
13. 假命题 15. 75° 16. -4 17. 66.5 18.①③④
19. 解:原式
当 时,原式 =
20. (1)证明:
∵ AD 是 BC边上的中线,
(2)解:
21. 解:步骤①、②有误,
原式
当 时,
原式
22. 证明:(1)∵BE⊥CD,AF⊥BE,
∴∠AFB=∠BEC=90°,∴∠ABE+∠BAF=90°.
∵∠ABC=90°,∴∠ABE+∠EBC=90°,
∴∠BAF=∠EBC.
在△ABF和△BCE中,
∴ △ABF≌△BCE(ASA).
(2)∵∠ABC=90°,∴∠ABD+∠DBC=90°.
∵∠BED=90°,∴∠DBE+∠BDE=90°,
∵BD平分∠ABE,∴∠ABD=∠DBE.
∴∠DBC=∠BDE.∴BC=CD,即△BCD是等腰三角形.
23. 解: 解得
(2) 由 ( 1 ) 可 得
同 理 可 得
所以原方程可变形为: 解得 经检验, 是原方程的解,所以原方程的解为
24. (1)证明:
又 在△BFD和△CAD中,
∴△BFD≌△CAD(AAS),∴BF=AC.
(2)证明:∵ BE平分∠ABC,∴∠ABE=∠CBE.
在△ABE和△CBE中,
∴△ABE≌△CBE(ASA),∴CE=AE,
又
(3)解:CE
∴DH⊥BC,BH=CH,
∴DH 为BC的垂直平分线,∴BG=CG.在 Rt△CEG中,CE
10)元,依题意,得50x+50(x+10)=7500,
解得x=70,∴x+10=80,
答:A,B两型自行车的单价分别是70元和80元.
问题2:
由题可得
解得a=15.经检验,a=15是所列方程的解,且符合题意,故a的值为15.
26. (1)证明:∵AE=MC,
∴BE=BM,∴∠BEM=∠EMB =45°,
∴∠AEM=135°.∵CN平分∠DCP,∴∠PCN=45°,
∴∠MCN=135°.∴∠AEM =∠MCN.
在△AEM和△MCN中,
∴△AEM≌△MCN(ASA),∴AM=MN.
(2)解:仍然成立.理由:如图,在边AB上截取AE=MC,连接ME.
∵ △ABC是等边三角形,
∴AB=BC,∠B=∠ACB=60°,
∴∠ACP=120°.
∵AE=MC,∴BE=BM,∴∠BEM=∠EMB=60°,
∴∠AEM=120°.
∵CN平分∠ACP,∴∠PCN=60°,
∴∠MCN=120°.∴∠AEM=∠MCN.
∵ ∠CMN=180°-∠AMN-∠AMB=180°-∠B --∠AMB
=∠BAM,∴∠CMN=∠EAM.
在△AEM 和△MCN中, ∴△AEM≌△MCN(ASA),∴AM=MN.
同课章节目录
