湘教版八年级上册数学第二章 三角形基础复习(1)(无答案)
文档属性
| 名称 | 湘教版八年级上册数学第二章 三角形基础复习(1)(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 548.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-18 08:57:38 | ||
图片预览

文档简介
第一章 三角形基础复习(1)
1.下列各组数中,能够作为直角三角形的三边长的一组是 ( )
A.1,2,3 B.2,3,4 C.4,5,6 D.3,4,5
2.如图,225、289分别表示上面两个正方形的面积,则字母A所代表的正方形的面积为 ( )
A.4 B.8 C.16 D.64
3.如图所示,在△ABC中,AB=AC=10cm,D是BC的中点,若AD=8cm,则BC的长度为 ( )
A.4cm B.6cm C.10cm D.12cm
4.如果把直角三角形的两条直角边同时扩大到原来的2 倍,那么斜边扩大到原来的 ( )
A.1倍 B.2倍 C.3倍 D.4倍
5.已知|a-6|+|b-8|+(c-10) =0,则以a,b,c为三边长的三角形是
( )
A.直角三角形 B.锐角三角形
C.等腰三角形 D.钝角三角形
6.如图,一艘轮船以16海里/时的速度从港口A 出发向东北方向航行,另一艘轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,两船相距 ( )
A.25海里
B.30海里
C.40海里
D.50海里
7.下列选项中,不能用来验证勾股定理的是 ( )
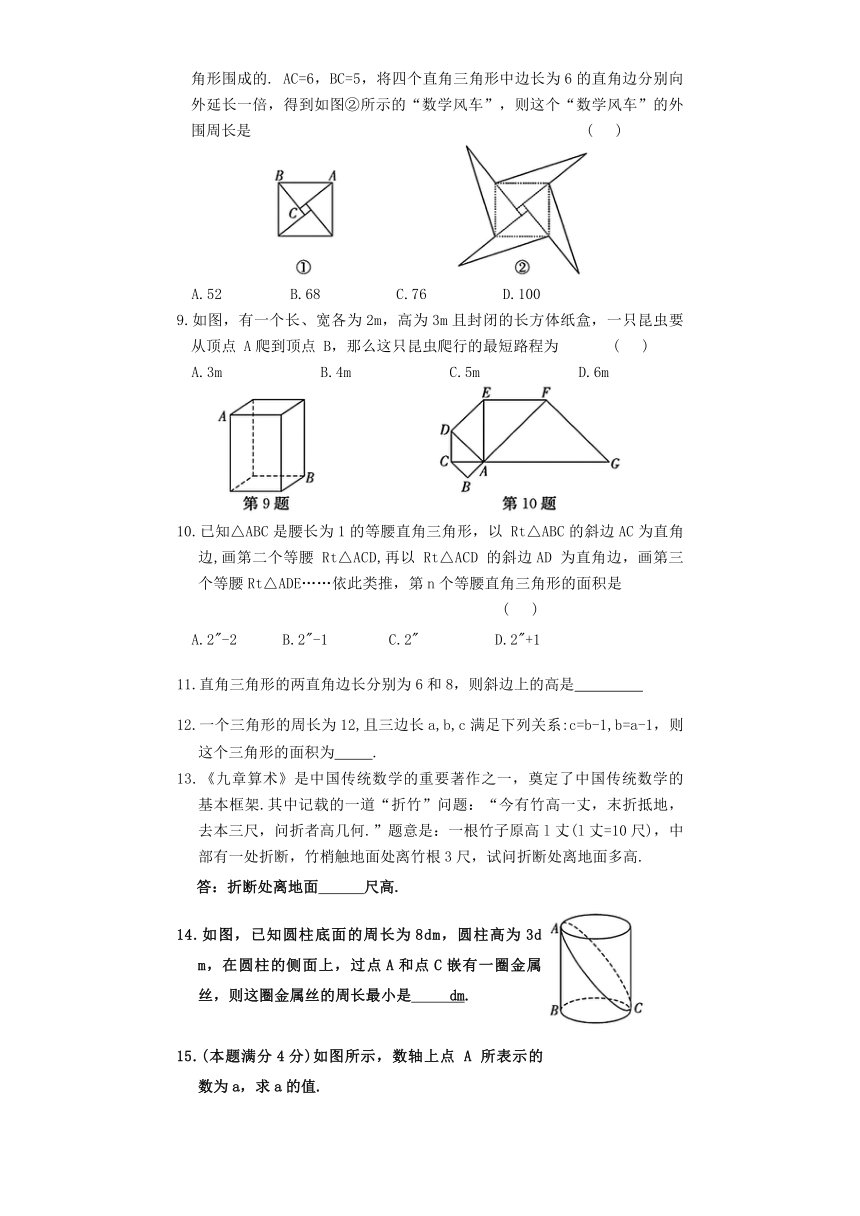
8.图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的. AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图②所示的“数学风车”,则这个“数学风车”的外围周长是 ( )
A.52 B.68 C.76 D.100
9.如图,有一个长、宽各为2m,高为3m且封闭的长方体纸盒,一只昆虫要从顶点 A爬到顶点 B,那么这只昆虫爬行的最短路程为 ( )
A.3m B.4m C.5m D.6m
10.已知△ABC是腰长为1的等腰直角三角形,以 Rt△ABC的斜边AC为直角边,画第二个等腰 Rt△ACD,再以 Rt△ACD 的斜边AD 为直角边,画第三个等腰Rt△ADE……依此类推,第n个等腰直角三角形的面积是 ( )
A.2"-2 B.2"-1 C.2" D.2"+1
11.直角三角形的两直角边长分别为6和8,则斜边上的高是
12.一个三角形的周长为12,且三边长a,b,c满足下列关系:c=b-1,b=a-1,则这个三角形的面积为 .
13.《九章算术》是中国传统数学的重要著作之一,奠定了中国传统数学的基本框架.其中记载的一道“折竹”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何.”题意是:一根竹子原高l丈(l丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高.
答:折断处离地面 尺高.
14.如图,已知圆柱底面的周长为8dm,圆柱高为3dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小是 dm.
15.(本题满分4分)如图所示,数轴上点 A 所表示的数为a,求a的值.
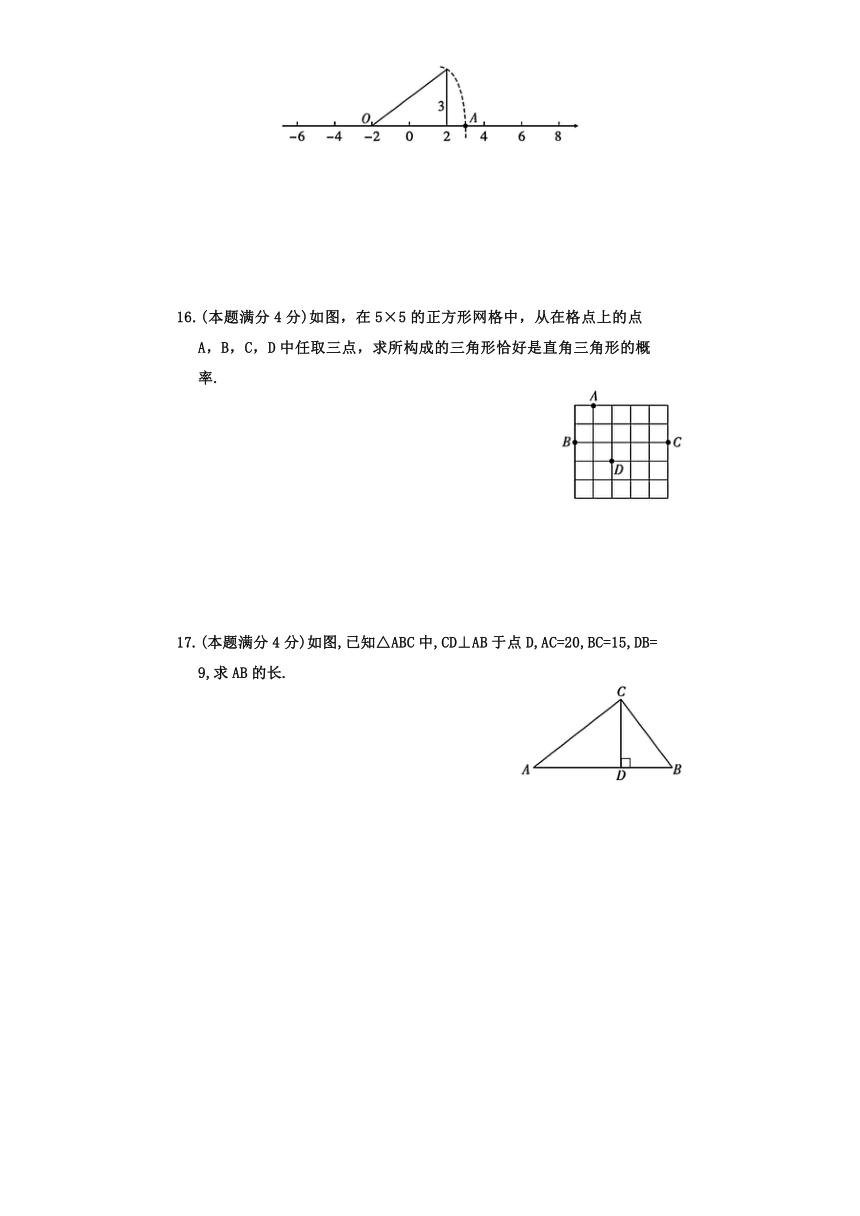
16.(本题满分4分)如图,在5×5的正方形网格中,从在格点上的点 A,B,C,D中任取三点,求所构成的三角形恰好是直角三角形的概率.
17.(本题满分4分)如图,已知△ABC中,CD⊥AB于点D,AC=20,BC=15,DB=9,求AB的长.
18.(本题满分4分)在 中, 的对边分别为a,b,c,如果 那么这个三角形是直角三角形吗 安安的解答如下:解:这个三角形不是直角三角形.理由如下:因为 所以 不是直角三角形.请问安安的解答正确吗 若不正确,请给出正确的解答过程,并画出这个直角三角形.
19.(本题满分6分)如图,四边形ABCD中,∠C=90°,BD平分∠ABC,AD=3,E为AB 上一点,AE=4,ED=5,求CD的长.
20.(本题满分6分)如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7,求四边形A,B,C,D的面积之和.
21.(本题满分6分)如图,瑞瑞想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面时还多1m,当他把绳子的下端拉开5m后,发现下端刚好接触地面,求旗杆的高度.
22.(本题满分6分)如图,有一块凹四边形土地ABCD,其中 ,求这块四边形土地的面积.
23.(本题满分7分)如图,在 和 中, 点A,C,D依次在同一直线上,且
(1)试说明:
(2)连接AE,当 时,求AE的长.
24.(本题满分9分)如图,A,B两村在河边CD 的同侧,A,B两村到河的距离分别为 又 ,现要在河边CD上建一水厂,同时分别向A,B两村输送自来水,铺设水管时工程费用为每千米20000元,请你在CD上选择水厂的位置O,使铺设水管的费用最省,并求出铺设水管的总费用.
25.(本题满分12分)阅读:能够成为直角三角形三条边长的三个正整数a,b,c,称为勾股数.世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》,其勾股数组公式为 其中m>n>0,m,n是互质的奇数.
应用:当n=1时,求有一边长为5的直角三角形的另外两条边长.
1.下列各组数中,能够作为直角三角形的三边长的一组是 ( )
A.1,2,3 B.2,3,4 C.4,5,6 D.3,4,5
2.如图,225、289分别表示上面两个正方形的面积,则字母A所代表的正方形的面积为 ( )
A.4 B.8 C.16 D.64
3.如图所示,在△ABC中,AB=AC=10cm,D是BC的中点,若AD=8cm,则BC的长度为 ( )
A.4cm B.6cm C.10cm D.12cm
4.如果把直角三角形的两条直角边同时扩大到原来的2 倍,那么斜边扩大到原来的 ( )
A.1倍 B.2倍 C.3倍 D.4倍
5.已知|a-6|+|b-8|+(c-10) =0,则以a,b,c为三边长的三角形是
( )
A.直角三角形 B.锐角三角形
C.等腰三角形 D.钝角三角形
6.如图,一艘轮船以16海里/时的速度从港口A 出发向东北方向航行,另一艘轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,两船相距 ( )
A.25海里
B.30海里
C.40海里
D.50海里
7.下列选项中,不能用来验证勾股定理的是 ( )
8.图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的. AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图②所示的“数学风车”,则这个“数学风车”的外围周长是 ( )
A.52 B.68 C.76 D.100
9.如图,有一个长、宽各为2m,高为3m且封闭的长方体纸盒,一只昆虫要从顶点 A爬到顶点 B,那么这只昆虫爬行的最短路程为 ( )
A.3m B.4m C.5m D.6m
10.已知△ABC是腰长为1的等腰直角三角形,以 Rt△ABC的斜边AC为直角边,画第二个等腰 Rt△ACD,再以 Rt△ACD 的斜边AD 为直角边,画第三个等腰Rt△ADE……依此类推,第n个等腰直角三角形的面积是 ( )
A.2"-2 B.2"-1 C.2" D.2"+1
11.直角三角形的两直角边长分别为6和8,则斜边上的高是
12.一个三角形的周长为12,且三边长a,b,c满足下列关系:c=b-1,b=a-1,则这个三角形的面积为 .
13.《九章算术》是中国传统数学的重要著作之一,奠定了中国传统数学的基本框架.其中记载的一道“折竹”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何.”题意是:一根竹子原高l丈(l丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高.
答:折断处离地面 尺高.
14.如图,已知圆柱底面的周长为8dm,圆柱高为3dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小是 dm.
15.(本题满分4分)如图所示,数轴上点 A 所表示的数为a,求a的值.
16.(本题满分4分)如图,在5×5的正方形网格中,从在格点上的点 A,B,C,D中任取三点,求所构成的三角形恰好是直角三角形的概率.
17.(本题满分4分)如图,已知△ABC中,CD⊥AB于点D,AC=20,BC=15,DB=9,求AB的长.
18.(本题满分4分)在 中, 的对边分别为a,b,c,如果 那么这个三角形是直角三角形吗 安安的解答如下:解:这个三角形不是直角三角形.理由如下:因为 所以 不是直角三角形.请问安安的解答正确吗 若不正确,请给出正确的解答过程,并画出这个直角三角形.
19.(本题满分6分)如图,四边形ABCD中,∠C=90°,BD平分∠ABC,AD=3,E为AB 上一点,AE=4,ED=5,求CD的长.
20.(本题满分6分)如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7,求四边形A,B,C,D的面积之和.
21.(本题满分6分)如图,瑞瑞想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面时还多1m,当他把绳子的下端拉开5m后,发现下端刚好接触地面,求旗杆的高度.
22.(本题满分6分)如图,有一块凹四边形土地ABCD,其中 ,求这块四边形土地的面积.
23.(本题满分7分)如图,在 和 中, 点A,C,D依次在同一直线上,且
(1)试说明:
(2)连接AE,当 时,求AE的长.
24.(本题满分9分)如图,A,B两村在河边CD 的同侧,A,B两村到河的距离分别为 又 ,现要在河边CD上建一水厂,同时分别向A,B两村输送自来水,铺设水管时工程费用为每千米20000元,请你在CD上选择水厂的位置O,使铺设水管的费用最省,并求出铺设水管的总费用.
25.(本题满分12分)阅读:能够成为直角三角形三条边长的三个正整数a,b,c,称为勾股数.世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》,其勾股数组公式为 其中m>n>0,m,n是互质的奇数.
应用:当n=1时,求有一边长为5的直角三角形的另外两条边长.
同课章节目录
