湘教版八年级上册数学第2章 三角形 基础复习(一)(含答案)
文档属性
| 名称 | 湘教版八年级上册数学第2章 三角形 基础复习(一)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 430.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-18 00:00:00 | ||
图片预览


文档简介
第2章基础复习(一)
知识点 1 三角形
1. 三角形的任意两边之和大于第三边.
2. 从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫作三角形的高线,简称三角形的高.在三角形中,一个角的平分线与这个角的对边相交,这个角的顶点与交点之间的线段叫作三角形的角平分线.在三角形中,连接一个顶点和它的对边中点的线段叫作三角形的中线.三角形的三条中线相交于一点,我们把这三条中线的交点叫作三角形的重心.
3. 三角形的内角和等于180°,三角形的一边与另一边的延长线所组成的角,叫作三角形的外角.
1.下列长度的三条线段,能组成三角形的是 ( )
A. 2,2,4 B. 5,6,12 C. 5,7,2 D. 6,8,10
2.如图,在 中,BE是 的平分线,CE是外角∠ACM的平分线,BE 与CE 相交于点 E,若 则 是 ( )
A. 15° B. 30° C. 45° D. 60°
3. 已知 的三边长分别为a,b,c,且. ,那么 ( )
A. M>0 C. M=0 D. M<0
4.如图所示的网格由边长相同的小正方形组成,点A,B,C,D,E,F,G在小正方形的顶点上,则 的重心是 ( )
A. 点D B. 点 E C. 点 F D. 点 G
5. 已知a,b,c为. 的三边长, 且a为方程|x-4|=2的解,请你求出△ABC的边长a.
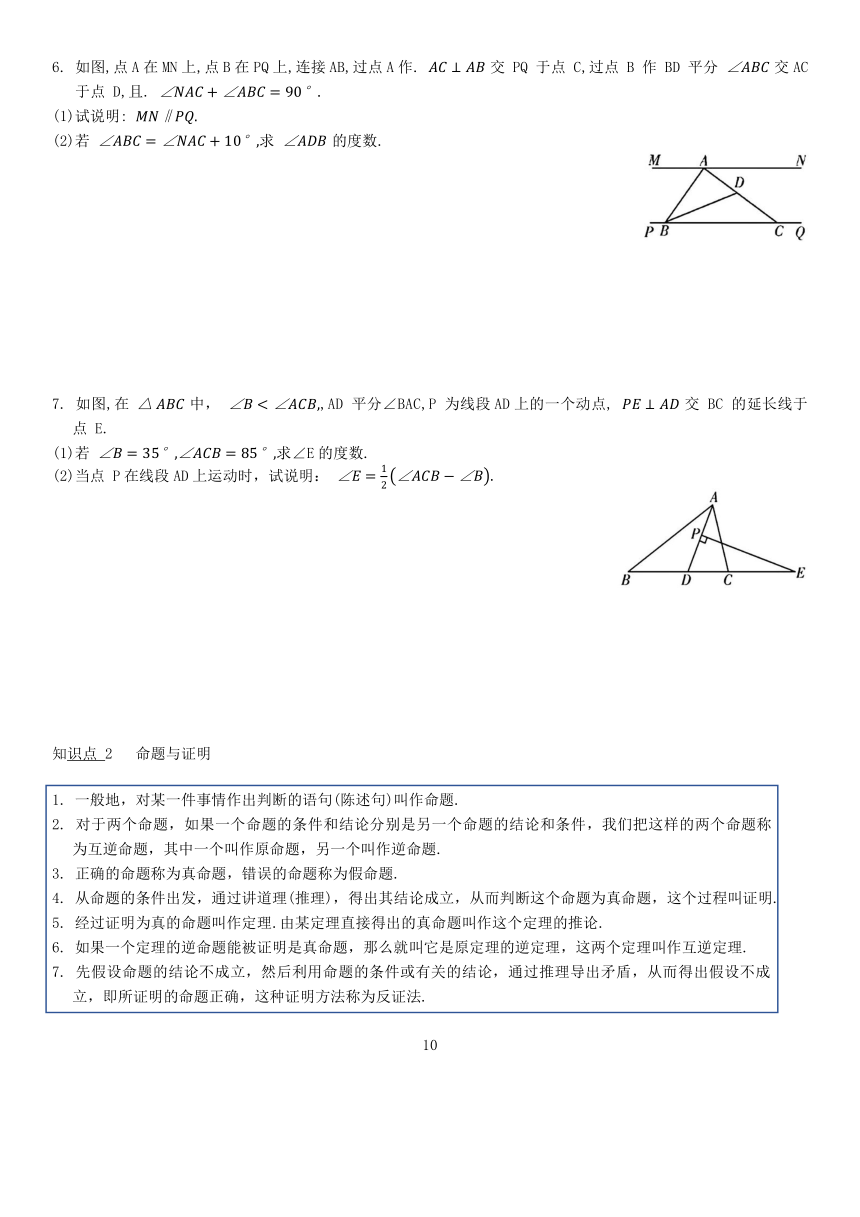
6. 如图,点A在MN上,点B在PQ上,连接AB,过点A作. 交 PQ 于点 C,过点 B 作 BD 平分 交AC于点 D,且.
(1)试说明:
(2)若 求 的度数.
7. 如图,在 中, ,AD 平分∠BAC,P 为线段AD上的一个动点, 交 BC 的延长线于点 E.
(1)若 求∠E的度数.
(2)当点 P在线段AD上运动时,试说明:
知识点 2 命题与证明
1. 一般地,对某一件事情作出判断的语句(陈述句)叫作命题.
2. 对于两个命题,如果一个命题的条件和结论分别是另一个命题的结论和条件,我们把这样的两个命题称为互逆命题,其中一个叫作原命题,另一个叫作逆命题.
3. 正确的命题称为真命题,错误的命题称为假命题.
4. 从命题的条件出发,通过讲道理(推理),得出其结论成立,从而判断这个命题为真命题,这个过程叫证明.
5. 经过证明为真的命题叫作定理.由某定理直接得出的真命题叫作这个定理的推论.
6. 如果一个定理的逆命题能被证明是真命题,那么就叫它是原定理的逆定理,这两个定理叫作互逆定理.
7. 先假设命题的结论不成立,然后利用命题的条件或有关的结论,通过推理导出矛盾,从而得出假设不成立,即所证明的命题正确,这种证明方法称为反证法.
10
8. 下列语句不是命题的是 ( )
A. 两点之间,线段最短 B. 连接AB 并延长至 C 点
C. 同旁内角互补 D. 同角的余角相等
9. 下列四个命题中,真命题有 ( )
①两直线被第三条直线所截,内错角相等.
②同一平面内,垂直于同一直线的两直线平行.
③三角形的一个外角大于任何一个内角.
④如果 那么x>0.
A. 1 个 B. 2 个 C. 3个 D. 4个
10. 把命题“对顶角相等”改写成“如果……那么………”的形式: .
11. 写出下列命题的逆命题,并判断原命题和逆命题的真假.
(1)若 则m≠n.
(2)如果一个三角形有一个内角是钝角,那么它的另外两个内角是锐角.
12. 如图所示,现有下列4个事项:
(1)∠1=∠2,(2)∠3=∠B,(3)FG⊥AB于点G,(4)CD⊥AB于点D.
以上述4个事项中的(1)、(2)、(3)作为一个命题的已知条件,(4)作为该命题的结论,可以组成一个真命题.请你证明这个真命题.
知识点 3 等腰三角形
1. 等腰三角形的性质定理:等腰三角形是轴对称图形,对称轴是顶角平分线所在的直线.等腰三角形底边上的高、中线及顶角平分线重合(简称“三线合一”).等腰三角形的两底角相等(简称“等边对等角”).
2. 等边三角形的性质定理:等边三角形的三个内角相等,且都等于 等边三角形是特殊的等腰三角形,因此等边三角形是轴对称图形,它有三条对称轴,分别是三个内角的平分线所在的直线.
3. 等腰三角形的判定定理:有两个角相等的三角形是等腰三角形(简称“等角对等边”).
4. 等边三角形的判定定理:三个角都是60°的三角形是等边三角形;有一个角是( 的等腰三角形是等边三角形.
11
13. 如图,AB∥CD,EF分别交AB,CD于点E,F,且MN=ME,若∠FMN=80°,则∠1的度数为
( )
A. 40° B. 50° C. 60° D. 80°
14.若一个等腰三角形的两边长分别为2,4,则第三边的长为 ( )
A. 2 B. (宁夏中考) 3 C. 4 D. 2或4
15.如图,在△ABC中,AC=BC,点D和E分别在AB和AC上,且AD=AE.连接DE,过点A 的直线 GH 与 DE 平行,若∠C=40°,则∠GAD的度数为 ( )
A. 40° B. 45° C. 55° D. 70°
16.如图,Rt△ABC中,∠A=90°,∠B=30°,CD=CA,D在BC上,∠ADE=45°,E在AB上,则∠BED的度数是 ( )
A. 60° B. 75° C. 80° D. 85°
17. 如图,△ABC中,BO平分∠ABC,CO平分∠ACB,M,N经过点O,且MN∥BC,若AB=5,△AMN的周长等于12,则AC的长为 ( )
A. 7 B. 6 C. 5 D. 4
18.如图,直线a∥b,△ABC的顶点 C在直线b上,边AB 与直线b相交于点 D.若△BCD是等边三角形,∠A=20°,则∠1= °.
19. 直线上依次有A,B,C,D四个点,AD=7,AB=2,若AB,BC,CD可构成以BC 为腰的等腰三角形,则BC的长为 .
20. 如图,在△ABC中,AB=AC,AD⊥BC于点D.
(1)若∠C=42°,求∠BAD的度数.
(2)若点 E在边AB上,EF∥AC交AD的延长线于点 F.求证:AE=FE.
第2章基础复习(一)
1. D 2. B 3. D 4. A
5. 解:因为a为方程|x-4|=2的解,所以a-4=±2,解得a=6或2.因为a,b,c为△ABC的边长,b+c=5<6,所以a=6不符合题意,舍去,所以a=2.
6. 解:(1)因为AC⊥AB,所以∠BAC=90°,
所以∠ABC+∠ACB=90°,
因为∠NAC+∠ABC=90°,
所以∠NAC=∠ACB,所以MN∥PQ.
(2)因为∠ABC=∠NAC+10°=∠ACB+10°,
∠ACB+∠ABC=90°,
所以∠ACB+∠ACB+10°=90°,
所以∠ACB=40°,所以∠ABC=50°,
因为BD平分∠ABC,所以
所以∠ADB=∠CBD+∠DCB=25°+40°=65°.
7. 解:(1)因为∠B=35°,∠ACB=85°,所以∠BAC=60°.
因为AD平分∠BAC,所以∠DAB=30°.
所以∠ADC=∠B+∠DAB=65°.
因为PE⊥AD,所以∠DPE=90°,所以∠E=90°-65°=25°.
(2)因为∠B+∠BAC+∠ACB=180°,
所以∠BAC=180°-(∠B+∠ACB).
因为AD平分∠BAC,
所以
所以
因为PE⊥AD,所以∠DPE=90°.
所以∠ADC+∠E=90°.所以∠E=90°-∠ADC,
即
8. B 9. A
10. 如果两个角是对顶角,那么这两个角相等.
11. 解:(1)逆命题:若m≠n,则 原命题是真命题,逆命题是假命题.
(2)逆命题:如果一个三角形有两个内角是锐角,那么这个三角形的另一个内角是钝角.原命题是真命题,逆命题是假命题.
12. 证明:∵∠3=∠B,∴DE∥BC,∴∠1=∠BCD.
∵ ∠1 =∠2,∴∠2=∠BCD,
所以GF∥CD,∴∠CDB=∠FGB.
∵ FG⊥AB,∴∠BGF=90°,
∴∠CDB=90°,∴CD⊥AB.
13. A 14. C 15. C 16. B 17. A
18. 40 19. 2或2.5
20. (1)解:∵AB=AC,AD⊥BC于点D,
∴∠BAD=∠CAD,∠ADC=90°,又∠C=42°,
∴∠BAD =∠CAD=90°-42°=48°.
(2)证明:由(1)知∠BAD=∠CAD.
∵EF∥AC,∴∠F=∠CAD,
∴∠BAD =∠F,∴AE=FE.
知识点 1 三角形
1. 三角形的任意两边之和大于第三边.
2. 从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫作三角形的高线,简称三角形的高.在三角形中,一个角的平分线与这个角的对边相交,这个角的顶点与交点之间的线段叫作三角形的角平分线.在三角形中,连接一个顶点和它的对边中点的线段叫作三角形的中线.三角形的三条中线相交于一点,我们把这三条中线的交点叫作三角形的重心.
3. 三角形的内角和等于180°,三角形的一边与另一边的延长线所组成的角,叫作三角形的外角.
1.下列长度的三条线段,能组成三角形的是 ( )
A. 2,2,4 B. 5,6,12 C. 5,7,2 D. 6,8,10
2.如图,在 中,BE是 的平分线,CE是外角∠ACM的平分线,BE 与CE 相交于点 E,若 则 是 ( )
A. 15° B. 30° C. 45° D. 60°
3. 已知 的三边长分别为a,b,c,且. ,那么 ( )
A. M>0 C. M=0 D. M<0
4.如图所示的网格由边长相同的小正方形组成,点A,B,C,D,E,F,G在小正方形的顶点上,则 的重心是 ( )
A. 点D B. 点 E C. 点 F D. 点 G
5. 已知a,b,c为. 的三边长, 且a为方程|x-4|=2的解,请你求出△ABC的边长a.
6. 如图,点A在MN上,点B在PQ上,连接AB,过点A作. 交 PQ 于点 C,过点 B 作 BD 平分 交AC于点 D,且.
(1)试说明:
(2)若 求 的度数.
7. 如图,在 中, ,AD 平分∠BAC,P 为线段AD上的一个动点, 交 BC 的延长线于点 E.
(1)若 求∠E的度数.
(2)当点 P在线段AD上运动时,试说明:
知识点 2 命题与证明
1. 一般地,对某一件事情作出判断的语句(陈述句)叫作命题.
2. 对于两个命题,如果一个命题的条件和结论分别是另一个命题的结论和条件,我们把这样的两个命题称为互逆命题,其中一个叫作原命题,另一个叫作逆命题.
3. 正确的命题称为真命题,错误的命题称为假命题.
4. 从命题的条件出发,通过讲道理(推理),得出其结论成立,从而判断这个命题为真命题,这个过程叫证明.
5. 经过证明为真的命题叫作定理.由某定理直接得出的真命题叫作这个定理的推论.
6. 如果一个定理的逆命题能被证明是真命题,那么就叫它是原定理的逆定理,这两个定理叫作互逆定理.
7. 先假设命题的结论不成立,然后利用命题的条件或有关的结论,通过推理导出矛盾,从而得出假设不成立,即所证明的命题正确,这种证明方法称为反证法.
10
8. 下列语句不是命题的是 ( )
A. 两点之间,线段最短 B. 连接AB 并延长至 C 点
C. 同旁内角互补 D. 同角的余角相等
9. 下列四个命题中,真命题有 ( )
①两直线被第三条直线所截,内错角相等.
②同一平面内,垂直于同一直线的两直线平行.
③三角形的一个外角大于任何一个内角.
④如果 那么x>0.
A. 1 个 B. 2 个 C. 3个 D. 4个
10. 把命题“对顶角相等”改写成“如果……那么………”的形式: .
11. 写出下列命题的逆命题,并判断原命题和逆命题的真假.
(1)若 则m≠n.
(2)如果一个三角形有一个内角是钝角,那么它的另外两个内角是锐角.
12. 如图所示,现有下列4个事项:
(1)∠1=∠2,(2)∠3=∠B,(3)FG⊥AB于点G,(4)CD⊥AB于点D.
以上述4个事项中的(1)、(2)、(3)作为一个命题的已知条件,(4)作为该命题的结论,可以组成一个真命题.请你证明这个真命题.
知识点 3 等腰三角形
1. 等腰三角形的性质定理:等腰三角形是轴对称图形,对称轴是顶角平分线所在的直线.等腰三角形底边上的高、中线及顶角平分线重合(简称“三线合一”).等腰三角形的两底角相等(简称“等边对等角”).
2. 等边三角形的性质定理:等边三角形的三个内角相等,且都等于 等边三角形是特殊的等腰三角形,因此等边三角形是轴对称图形,它有三条对称轴,分别是三个内角的平分线所在的直线.
3. 等腰三角形的判定定理:有两个角相等的三角形是等腰三角形(简称“等角对等边”).
4. 等边三角形的判定定理:三个角都是60°的三角形是等边三角形;有一个角是( 的等腰三角形是等边三角形.
11
13. 如图,AB∥CD,EF分别交AB,CD于点E,F,且MN=ME,若∠FMN=80°,则∠1的度数为
( )
A. 40° B. 50° C. 60° D. 80°
14.若一个等腰三角形的两边长分别为2,4,则第三边的长为 ( )
A. 2 B. (宁夏中考) 3 C. 4 D. 2或4
15.如图,在△ABC中,AC=BC,点D和E分别在AB和AC上,且AD=AE.连接DE,过点A 的直线 GH 与 DE 平行,若∠C=40°,则∠GAD的度数为 ( )
A. 40° B. 45° C. 55° D. 70°
16.如图,Rt△ABC中,∠A=90°,∠B=30°,CD=CA,D在BC上,∠ADE=45°,E在AB上,则∠BED的度数是 ( )
A. 60° B. 75° C. 80° D. 85°
17. 如图,△ABC中,BO平分∠ABC,CO平分∠ACB,M,N经过点O,且MN∥BC,若AB=5,△AMN的周长等于12,则AC的长为 ( )
A. 7 B. 6 C. 5 D. 4
18.如图,直线a∥b,△ABC的顶点 C在直线b上,边AB 与直线b相交于点 D.若△BCD是等边三角形,∠A=20°,则∠1= °.
19. 直线上依次有A,B,C,D四个点,AD=7,AB=2,若AB,BC,CD可构成以BC 为腰的等腰三角形,则BC的长为 .
20. 如图,在△ABC中,AB=AC,AD⊥BC于点D.
(1)若∠C=42°,求∠BAD的度数.
(2)若点 E在边AB上,EF∥AC交AD的延长线于点 F.求证:AE=FE.
第2章基础复习(一)
1. D 2. B 3. D 4. A
5. 解:因为a为方程|x-4|=2的解,所以a-4=±2,解得a=6或2.因为a,b,c为△ABC的边长,b+c=5<6,所以a=6不符合题意,舍去,所以a=2.
6. 解:(1)因为AC⊥AB,所以∠BAC=90°,
所以∠ABC+∠ACB=90°,
因为∠NAC+∠ABC=90°,
所以∠NAC=∠ACB,所以MN∥PQ.
(2)因为∠ABC=∠NAC+10°=∠ACB+10°,
∠ACB+∠ABC=90°,
所以∠ACB+∠ACB+10°=90°,
所以∠ACB=40°,所以∠ABC=50°,
因为BD平分∠ABC,所以
所以∠ADB=∠CBD+∠DCB=25°+40°=65°.
7. 解:(1)因为∠B=35°,∠ACB=85°,所以∠BAC=60°.
因为AD平分∠BAC,所以∠DAB=30°.
所以∠ADC=∠B+∠DAB=65°.
因为PE⊥AD,所以∠DPE=90°,所以∠E=90°-65°=25°.
(2)因为∠B+∠BAC+∠ACB=180°,
所以∠BAC=180°-(∠B+∠ACB).
因为AD平分∠BAC,
所以
所以
因为PE⊥AD,所以∠DPE=90°.
所以∠ADC+∠E=90°.所以∠E=90°-∠ADC,
即
8. B 9. A
10. 如果两个角是对顶角,那么这两个角相等.
11. 解:(1)逆命题:若m≠n,则 原命题是真命题,逆命题是假命题.
(2)逆命题:如果一个三角形有两个内角是锐角,那么这个三角形的另一个内角是钝角.原命题是真命题,逆命题是假命题.
12. 证明:∵∠3=∠B,∴DE∥BC,∴∠1=∠BCD.
∵ ∠1 =∠2,∴∠2=∠BCD,
所以GF∥CD,∴∠CDB=∠FGB.
∵ FG⊥AB,∴∠BGF=90°,
∴∠CDB=90°,∴CD⊥AB.
13. A 14. C 15. C 16. B 17. A
18. 40 19. 2或2.5
20. (1)解:∵AB=AC,AD⊥BC于点D,
∴∠BAD=∠CAD,∠ADC=90°,又∠C=42°,
∴∠BAD =∠CAD=90°-42°=48°.
(2)证明:由(1)知∠BAD=∠CAD.
∵EF∥AC,∴∠F=∠CAD,
∴∠BAD =∠F,∴AE=FE.
同课章节目录
