湘教版八年级上册数学 第2章三角形基础复习 (二)(含答案)
文档属性
| 名称 | 湘教版八年级上册数学 第2章三角形基础复习 (二)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 871.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-18 09:29:09 | ||
图片预览


文档简介
第2章基础复习 (二)
知识点 1 线段的垂直平分线
1. 线段垂直平分线的性质定理:线段垂直平分线上的点到线段两端的距离相等.
2. 垂直平分线的性质定理的逆定理:到线段两端距离相等的点在线段的垂直平分线上.
3. 尺规作图:作线段的垂直平分线;过一点作已知直线的垂线.
1.在平面内,有一个点到三角形三个顶点的距离相等,则这个点一定是三角形 ( )
A. 三条角平分线的交点 B. 三条高线的交点
C. 三条中线的交点 D. 三条边垂直平分线的交点
2.如图,在 中,AB的垂直平分线交AB 于点 D,交 BC于点E,若 BC=6,AC=5,则 的周长为 ( )
A. 8 B. 11 C. 16 D. 17
3. 如图,△ABC中,D,E两点分别在AC,BC上,DE为BC的垂直平分线,BD为∠ADE的角平分线.若 ,则∠ABD的度数为 ( )
A. 58° C. 61° D. 62°
4. 如图, 点C 在AE的垂直平分线上,则AB,AC,CE的长度关系为 ( )
A. AB>AC=CE C. AB>AC>CE D. AB=AC=CE
5. 如图,在已知的△ABC中,按以下步骤作图:①分别以 B,C为圆心,以大于 的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点 D,连接CD.若AD=AC,∠A=80°,则∠ACB 的度数为 ( )
A. 65° B. 70° C. 75° D. 80°
6. 在 中, ,AB 的垂直平分线 DE 交AC 于点 D,连接BD,则∠ABD = 度.
7. 如图,在 中, ,AB的垂直平分线分别交AB,BC于点 D,E,AC的垂直平分线分别交AC,BC于点 F,G.则 的周长为 .
13
8. 已知, 是等边三角形,过点C 作( 且 ,连接BD交AC于点 O.
(1)如图1,求证:AC垂直平分 BD.
(2)如图2,点M在BC的延长线上,点 N在线段CO上,且ND=NM,连接BN.求证:NB=NM.
知识点 2 全等三角形
1. 能够完全重合的两个图形叫作全等图形.
2. 全等三角形的对应边相等;全等三角形的对应角相等.
3. 全等三角形的判定:
①两边及其夹角分别相等的两个三角形全等.(简写成“边角边”或“SAS”)
②两角及其夹边分别相等的两个三角形全等.(简写成“角边角”或“ASA”)
③两角分别相等且其中一组等角的对边相等的两个三角形全等.(简写成“角角边”或“AAS”)
④三边分别相等的两个三角形全等.(简写成“边边边”或“SSS”)
4. 只要三角形三边的长度确定,那么这个三角形的形状和大小就固定了,三角形的这个性质叫作三角形的稳定性.
9.下列图形中,具有稳定性的是 ( )
10. 一块三角形玻璃被打碎后,店员带着如图所示的一片碎玻璃去重新配一块与原来全等的三角形玻璃,能够全等的依据是 ( )
A. ASA B. AAS C. SAS D. SSS
11.如图,△ABC≌△DEF,DF和AC,EF和BC 为对应边,若∠A=123°,∠F=39°,则∠DEF等于
( )
A. 18° B. 20° C. 39° D. 123°
12.如图,已知AB=AC,点D,E分别在线段AB,AC上,BE与CD相交于点O,添加以下哪个条件仍不能判定△ABE≌△ACD ( )
A.∠B=∠C B. AE=AD C. BD=CE D. BE=CD
13. 如图,△ABC的面积为S,AD平分∠BAC,AD⊥BD于点D,连接CD,则△ACD 的面积为 ( )
A. B. S/ C D. S
14
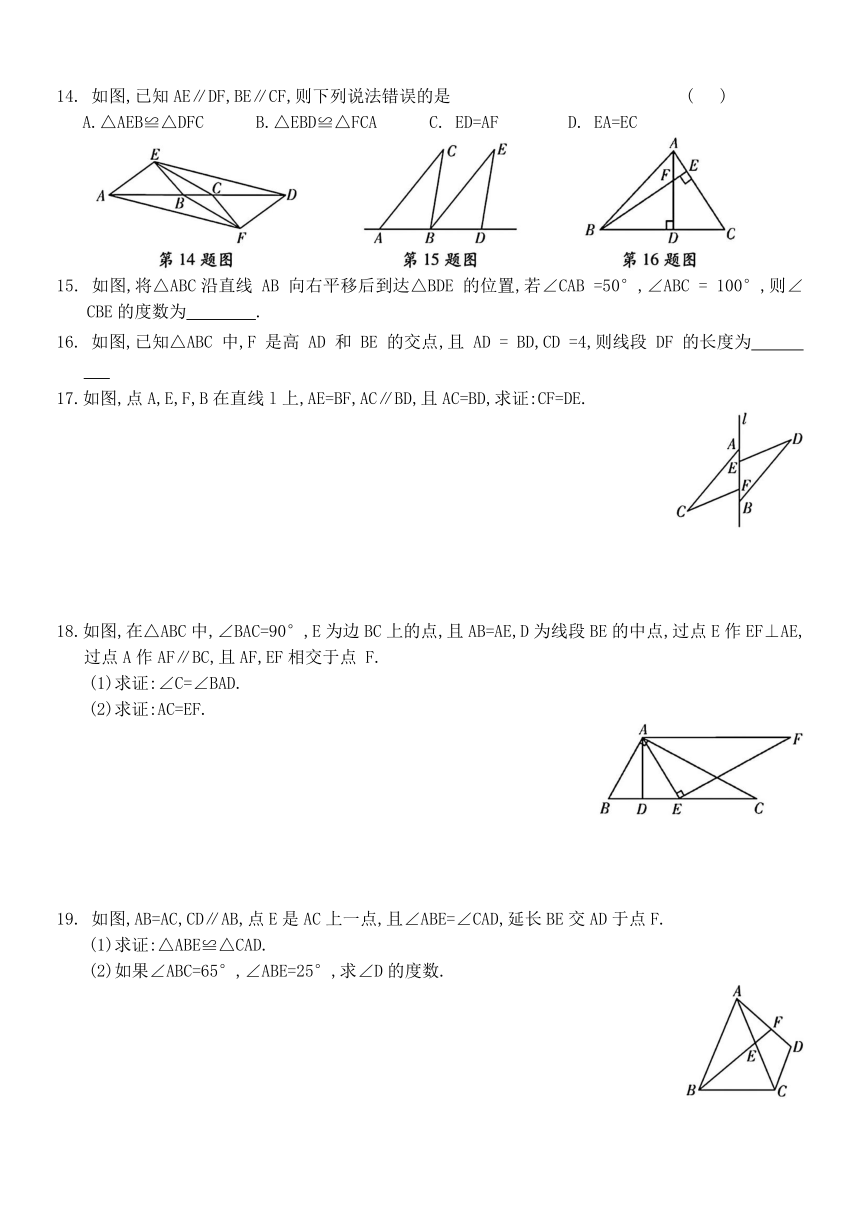
14. 如图,已知AE∥DF,BE∥CF,则下列说法错误的是 ( )
A.△AEB≌△DFC B.△EBD≌△FCA C. ED=AF D. EA=EC
15. 如图,将△ABC沿直线 AB 向右平移后到达△BDE 的位置,若∠CAB =50°,∠ABC = 100°,则∠CBE的度数为 .
16. 如图,已知△ABC 中,F 是高 AD 和 BE 的交点,且 AD = BD,CD =4,则线段 DF 的长度为
17.如图,点A,E,F,B在直线l上,AE=BF,AC∥BD,且AC=BD,求证:CF=DE.
18.如图,在△ABC中,∠BAC=90°,E为边BC上的点,且AB=AE,D为线段BE的中点,过点E作EF⊥AE,过点A作AF∥BC,且AF,EF相交于点 F.
(1)求证:∠C=∠BAD.
(2)求证:AC=EF.
19. 如图,AB=AC,CD∥AB,点E是AC上一点,且∠ABE=∠CAD,延长BE交AD于点F.
(1)求证:△ABE≌△CAD.
(2)如果∠ABC=65°,∠ABE=25°,求∠D的度数.
20. 如图1, 垂足分别为A,B, .点 P 在线段AB上以 2cm /s的速度由点 A 向点 B 运动,同时点 Q 在射线 BD上运动,它们运动的时间为t(s)(当点 P 运动结束时,点Q运动随之结束).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,并判断此时线段 PC 和线段 PQ 的位置关系,并说明理由.
(2)如图2,若“ '改为“∠CAB=∠DBA”,点Q 的运动速度为 xcm/s,其他条件不变,当点P,Q运动到何处时有△ACP与 全等,求出相应的x的值.
知识点 3 用尺规作三角形
①作一个角的平分线;②作一个角等于已知角;③作三角形.
21. 用直尺和圆规作一个角等于已知角,如图,能得出, 的依据是 ( )
A. SAS B. SSS C. ASA D. AAS
22. 已知线段a, 以a,b为边长作等腰三角形,则 ( )
A. 只能作以a为底边的等腰三角形 B. 只能作以b为底边的等腰三角形
C. 可以作分别以a,b为底边的等腰三角形 D. 不能作符合条件的等腰三角形
23. 如图,在 中,
(1)作 的平分线AD交BC于点D.(不写作法,保留作图痕迹)
(2)已知 求∠B的度数.
第 2 章基础复习(二)
1. D 2. B 3. D 4. D 5. C 6. 35 7. 10
8. 证明:(1)∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠CAB=60°,AB=BC.
∵CD∥AB,且CD=AB,
∴CD=BC,∠ACD=∠BAC=60°,
∴∠ACD=∠ACB.
∴BO=DO,CO⊥BD,∴AC垂直平分BD.
(2)由(1)知AC垂直平分 BD,∴NB=ND,∵ND=NM,∴NB=NM.
9. B 10. A 11. A 12. D 13. C 14. D 15. 30° 16. 4
17. 证明:∵AE=BF,∴AE+EF=BF+EF,即AF=BE,
∵AC∥BD,∴∠CAF=∠DBE,
在△ACF和△BDE中,
∴△ACF≌△BDE(SAS),∴CF=DE.
18. 证明:(1)∵AB=AE,D为线段 BE的中点,
∴AD⊥BC,∴∠ADC=90°,∴∠C+∠DAC=90°,
∵∠BAC=90°,∴∠BAD+∠DAC=90°,∴∠C=∠BAD.
(2)∵AF∥BC,∴∠FAE=∠AEB,
∵AB=AE,∴∠B=∠AEB,∴∠B=∠FAE,
∵EF⊥AE,∴∠AEF=90°=∠BAC,
又AB=EA,∴△ABC≌△EAF(ASA),∴AC=EF.
19. (1)证明:∵CD∥AB,∴∠BAE=∠ACD,
∵ ∠ABE=∠CAD,AB=CA,
∴△ABE≌△CAD(ASA).
(2)解:∵AB=AC,∴∠ACB=∠ABC=65°,
∴∠BAC=180°-∠ABC-∠ACB=180°-65°-65°=50°,
又∠CAD =∠ABE=25°,
∴∠BAD=∠BAC+∠CAD=50°+25°=75°,
∵AB∥CD,∴∠D=180°-∠BAD=180°-75°=105°.
20. 解:(1)△ACP≌△BPQ,PC⊥PQ.
理由如下:∵AC⊥AB,BD⊥AB,∴∠A=∠B=90°,当t=1时,AP=BQ=2,∵AB=7,∴BP=5,∴BP=AC,
∴△ACP≌△BPQ(SAS),∴∠C=∠BPQ,
∵∠C+∠APC=90°,∴∠APC+∠BPQ=90°,
∴∠CPQ=90°,∴PC⊥PQ.
(2) ①若△ACP≌△BPQ,则 AC = BP,AP = BQ,可得 解得
②若 △ACP ≌ △BQP, 则 AC = BQ,AP = BP, 可 得 解得 综上所述,当△ACP 与△BPQ 全等时,x的值为2或
21. B 22. B
23. 解:(1)如图所示,线段AD即为所求.
(2)∵AD平分∠BAC,∴∠BAD=∠CAD,∵AD=BD,∴∠B=∠BAD,∴∠B=∠CAD,又∠C=90°,∴∠B=30°.
知识点 1 线段的垂直平分线
1. 线段垂直平分线的性质定理:线段垂直平分线上的点到线段两端的距离相等.
2. 垂直平分线的性质定理的逆定理:到线段两端距离相等的点在线段的垂直平分线上.
3. 尺规作图:作线段的垂直平分线;过一点作已知直线的垂线.
1.在平面内,有一个点到三角形三个顶点的距离相等,则这个点一定是三角形 ( )
A. 三条角平分线的交点 B. 三条高线的交点
C. 三条中线的交点 D. 三条边垂直平分线的交点
2.如图,在 中,AB的垂直平分线交AB 于点 D,交 BC于点E,若 BC=6,AC=5,则 的周长为 ( )
A. 8 B. 11 C. 16 D. 17
3. 如图,△ABC中,D,E两点分别在AC,BC上,DE为BC的垂直平分线,BD为∠ADE的角平分线.若 ,则∠ABD的度数为 ( )
A. 58° C. 61° D. 62°
4. 如图, 点C 在AE的垂直平分线上,则AB,AC,CE的长度关系为 ( )
A. AB>AC=CE C. AB>AC>CE D. AB=AC=CE
5. 如图,在已知的△ABC中,按以下步骤作图:①分别以 B,C为圆心,以大于 的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点 D,连接CD.若AD=AC,∠A=80°,则∠ACB 的度数为 ( )
A. 65° B. 70° C. 75° D. 80°
6. 在 中, ,AB 的垂直平分线 DE 交AC 于点 D,连接BD,则∠ABD = 度.
7. 如图,在 中, ,AB的垂直平分线分别交AB,BC于点 D,E,AC的垂直平分线分别交AC,BC于点 F,G.则 的周长为 .
13
8. 已知, 是等边三角形,过点C 作( 且 ,连接BD交AC于点 O.
(1)如图1,求证:AC垂直平分 BD.
(2)如图2,点M在BC的延长线上,点 N在线段CO上,且ND=NM,连接BN.求证:NB=NM.
知识点 2 全等三角形
1. 能够完全重合的两个图形叫作全等图形.
2. 全等三角形的对应边相等;全等三角形的对应角相等.
3. 全等三角形的判定:
①两边及其夹角分别相等的两个三角形全等.(简写成“边角边”或“SAS”)
②两角及其夹边分别相等的两个三角形全等.(简写成“角边角”或“ASA”)
③两角分别相等且其中一组等角的对边相等的两个三角形全等.(简写成“角角边”或“AAS”)
④三边分别相等的两个三角形全等.(简写成“边边边”或“SSS”)
4. 只要三角形三边的长度确定,那么这个三角形的形状和大小就固定了,三角形的这个性质叫作三角形的稳定性.
9.下列图形中,具有稳定性的是 ( )
10. 一块三角形玻璃被打碎后,店员带着如图所示的一片碎玻璃去重新配一块与原来全等的三角形玻璃,能够全等的依据是 ( )
A. ASA B. AAS C. SAS D. SSS
11.如图,△ABC≌△DEF,DF和AC,EF和BC 为对应边,若∠A=123°,∠F=39°,则∠DEF等于
( )
A. 18° B. 20° C. 39° D. 123°
12.如图,已知AB=AC,点D,E分别在线段AB,AC上,BE与CD相交于点O,添加以下哪个条件仍不能判定△ABE≌△ACD ( )
A.∠B=∠C B. AE=AD C. BD=CE D. BE=CD
13. 如图,△ABC的面积为S,AD平分∠BAC,AD⊥BD于点D,连接CD,则△ACD 的面积为 ( )
A. B. S/ C D. S
14
14. 如图,已知AE∥DF,BE∥CF,则下列说法错误的是 ( )
A.△AEB≌△DFC B.△EBD≌△FCA C. ED=AF D. EA=EC
15. 如图,将△ABC沿直线 AB 向右平移后到达△BDE 的位置,若∠CAB =50°,∠ABC = 100°,则∠CBE的度数为 .
16. 如图,已知△ABC 中,F 是高 AD 和 BE 的交点,且 AD = BD,CD =4,则线段 DF 的长度为
17.如图,点A,E,F,B在直线l上,AE=BF,AC∥BD,且AC=BD,求证:CF=DE.
18.如图,在△ABC中,∠BAC=90°,E为边BC上的点,且AB=AE,D为线段BE的中点,过点E作EF⊥AE,过点A作AF∥BC,且AF,EF相交于点 F.
(1)求证:∠C=∠BAD.
(2)求证:AC=EF.
19. 如图,AB=AC,CD∥AB,点E是AC上一点,且∠ABE=∠CAD,延长BE交AD于点F.
(1)求证:△ABE≌△CAD.
(2)如果∠ABC=65°,∠ABE=25°,求∠D的度数.
20. 如图1, 垂足分别为A,B, .点 P 在线段AB上以 2cm /s的速度由点 A 向点 B 运动,同时点 Q 在射线 BD上运动,它们运动的时间为t(s)(当点 P 运动结束时,点Q运动随之结束).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,并判断此时线段 PC 和线段 PQ 的位置关系,并说明理由.
(2)如图2,若“ '改为“∠CAB=∠DBA”,点Q 的运动速度为 xcm/s,其他条件不变,当点P,Q运动到何处时有△ACP与 全等,求出相应的x的值.
知识点 3 用尺规作三角形
①作一个角的平分线;②作一个角等于已知角;③作三角形.
21. 用直尺和圆规作一个角等于已知角,如图,能得出, 的依据是 ( )
A. SAS B. SSS C. ASA D. AAS
22. 已知线段a, 以a,b为边长作等腰三角形,则 ( )
A. 只能作以a为底边的等腰三角形 B. 只能作以b为底边的等腰三角形
C. 可以作分别以a,b为底边的等腰三角形 D. 不能作符合条件的等腰三角形
23. 如图,在 中,
(1)作 的平分线AD交BC于点D.(不写作法,保留作图痕迹)
(2)已知 求∠B的度数.
第 2 章基础复习(二)
1. D 2. B 3. D 4. D 5. C 6. 35 7. 10
8. 证明:(1)∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠CAB=60°,AB=BC.
∵CD∥AB,且CD=AB,
∴CD=BC,∠ACD=∠BAC=60°,
∴∠ACD=∠ACB.
∴BO=DO,CO⊥BD,∴AC垂直平分BD.
(2)由(1)知AC垂直平分 BD,∴NB=ND,∵ND=NM,∴NB=NM.
9. B 10. A 11. A 12. D 13. C 14. D 15. 30° 16. 4
17. 证明:∵AE=BF,∴AE+EF=BF+EF,即AF=BE,
∵AC∥BD,∴∠CAF=∠DBE,
在△ACF和△BDE中,
∴△ACF≌△BDE(SAS),∴CF=DE.
18. 证明:(1)∵AB=AE,D为线段 BE的中点,
∴AD⊥BC,∴∠ADC=90°,∴∠C+∠DAC=90°,
∵∠BAC=90°,∴∠BAD+∠DAC=90°,∴∠C=∠BAD.
(2)∵AF∥BC,∴∠FAE=∠AEB,
∵AB=AE,∴∠B=∠AEB,∴∠B=∠FAE,
∵EF⊥AE,∴∠AEF=90°=∠BAC,
又AB=EA,∴△ABC≌△EAF(ASA),∴AC=EF.
19. (1)证明:∵CD∥AB,∴∠BAE=∠ACD,
∵ ∠ABE=∠CAD,AB=CA,
∴△ABE≌△CAD(ASA).
(2)解:∵AB=AC,∴∠ACB=∠ABC=65°,
∴∠BAC=180°-∠ABC-∠ACB=180°-65°-65°=50°,
又∠CAD =∠ABE=25°,
∴∠BAD=∠BAC+∠CAD=50°+25°=75°,
∵AB∥CD,∴∠D=180°-∠BAD=180°-75°=105°.
20. 解:(1)△ACP≌△BPQ,PC⊥PQ.
理由如下:∵AC⊥AB,BD⊥AB,∴∠A=∠B=90°,当t=1时,AP=BQ=2,∵AB=7,∴BP=5,∴BP=AC,
∴△ACP≌△BPQ(SAS),∴∠C=∠BPQ,
∵∠C+∠APC=90°,∴∠APC+∠BPQ=90°,
∴∠CPQ=90°,∴PC⊥PQ.
(2) ①若△ACP≌△BPQ,则 AC = BP,AP = BQ,可得 解得
②若 △ACP ≌ △BQP, 则 AC = BQ,AP = BP, 可 得 解得 综上所述,当△ACP 与△BPQ 全等时,x的值为2或
21. B 22. B
23. 解:(1)如图所示,线段AD即为所求.
(2)∵AD平分∠BAC,∴∠BAD=∠CAD,∵AD=BD,∴∠B=∠BAD,∴∠B=∠CAD,又∠C=90°,∴∠B=30°.
同课章节目录
