2.5　矩形 矩形的判定 课件

课件14张PPT。矩形的判定1、平行四边形的对边___________,
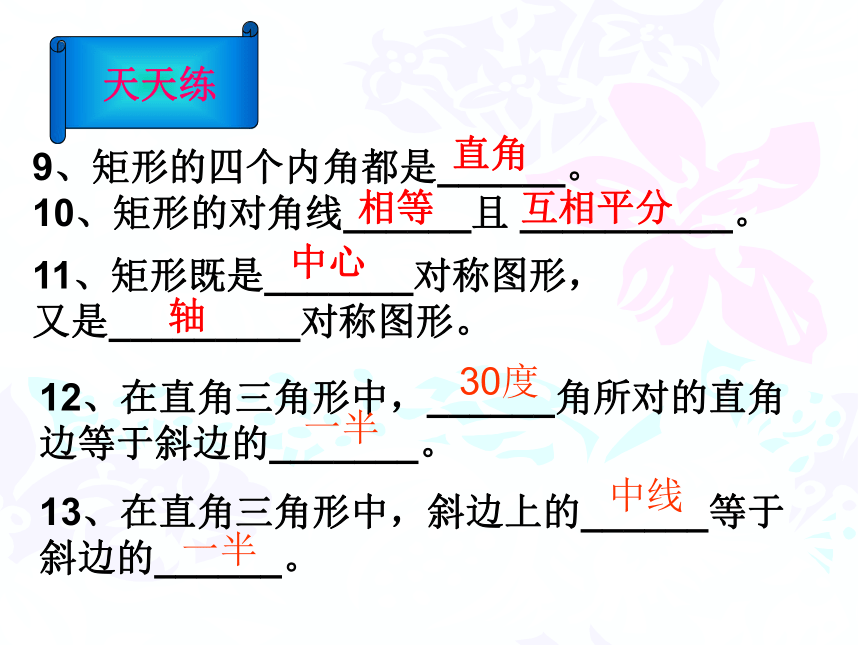
对角________,邻角_____________平行且相等3、平行四边形是______________ 平分相等4、平行线之间的______处处相等。距离互补2、平行四边形的对角线互相______. 中心对称图形 ６、一组对边______且______的四边形是平行 四边形。平行相等５、两组对边______的四边形是平行四边形。相等４、两组对边______的四边形是平行四边形。平行8、对角线__________的四边形是平行四边形。7、两组对角______的四边形是平行四边形。互相平分相等9、矩形的四个内角都是______。
10、矩形的对角线______且 __________。直角相等互相平分11、矩形既是_______对称图形，
又是_________对称图形。中心轴12、在直角三角形中，______角所对的直角边等于斜边的_______。
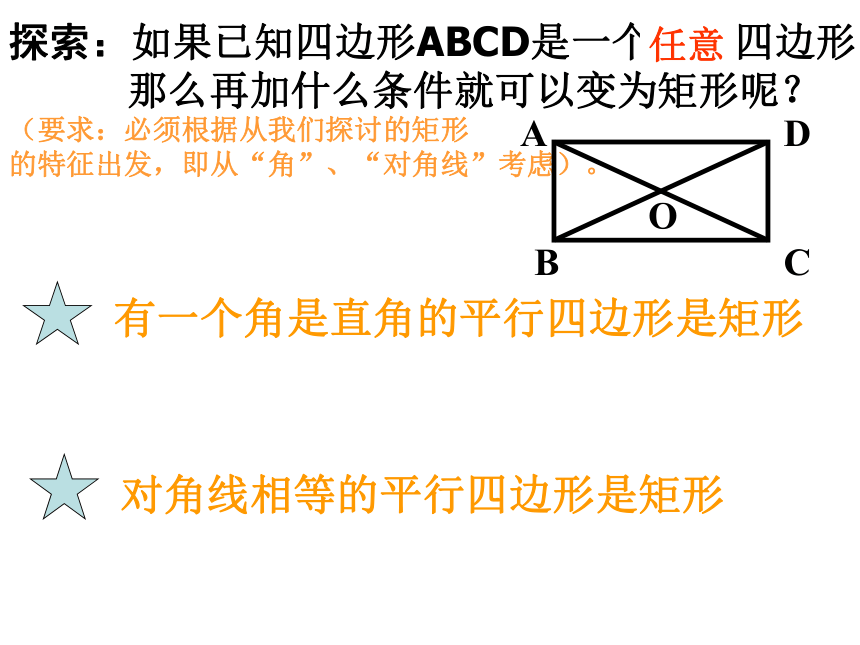
13、在直角三角形中，斜边上的______等于斜边的______。30度一半中线一半探索：如果已知四边形ABCD是一个平行四边形
那么再加什么条件就可以变为矩形呢？
（要求：必须根据从我们探讨的矩形
的特征出发，即从“角”、“对角线”考虑）。有一个角是直角的平行四边形是矩形 对角线相等的平行四边形是矩形 任意对角线相等的平行四边形是矩形。已知：平行四边形ABCD，AC=BD。
求证：四边形ABCD是矩形。证明: ∵ AB=CD, BC=BC, AC=BD∴ △ABC≌ △DCB（SSS）∵ AB//CD
∴ ∠ABC+∠DCB=180° ∴ ∠ABC=∠DCB=90°
又∵ 四边形ABCD是平行四边形∴四边形ABCD是矩形∴ ∠ABC=∠DCB有一个角是直角
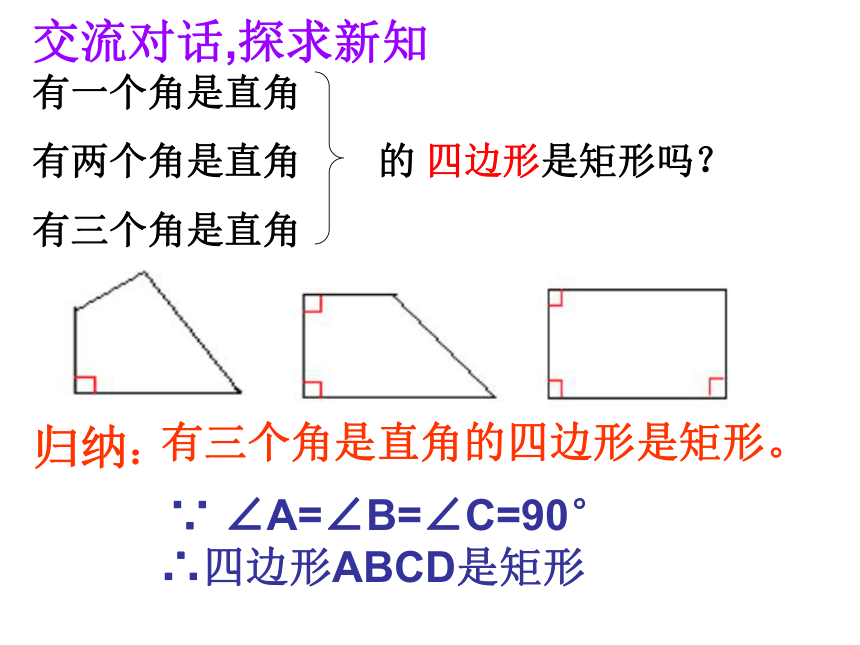
有两个角是直角 的 四边形是矩形吗？
有三个角是直角
交流对话,探求新知归纳：有三个角是直角的四边形是矩形。 ∵ ∠A=∠B=∠C=90°
∴四边形ABCD是矩形交流对话,探求新知思考：(1)对角线相等的四边形是矩形吗? (2)需要添加什么条件才能使 对角线相等的四边形是矩形吗?归纳：对角线相等且互相平分的四边形
是矩形 ∵ AC=BD
且OA=OC OB=OD
∴四边形ABCD是矩形等腰梯形你能归纳矩形特有的几种识别方法吗？有一个角是直角的平行四边形是
矩形 （定义）对角线相等的平行四边形是矩形 有三个角是直角的四边形是矩形 对角线相等且互相平分的四边形
是矩形 判断下列说法是否正确？⑴对角线相等的四边形是矩形； （ ）⑵对角线互相平分且相等的四边形是矩形（ ）⑶有一个角是直角的四边形是矩形； （ ）⑷有三个角是直角的四边形是矩形； （ ）⑸四个角都相等的四边形是矩形； （ ）⑹对角线相等，且有一个角是直角的四边形
是矩形； （ ）⑺对角线相等且互相垂直的四边形是矩形。 （ ）例1、已知如图四边形ABCD中AB⊥BC，
AD∥BC，AD=BC，试说明四边形ABCD
是矩形。证明：∵ AD=CB AD∥CB
∴四边形ABCD是平行四边形
∵AB⊥BC
∴∠B=90°
∴ □ ABCD是矩形练习：已知如图四边形ABCD中
AO=BO=CO=DO，试说明四
边形ABCD是矩形。例2、BD、BE分别是∠ABC与它的邻补角的平分线，AE⊥BE，AD⊥BD，求证：四边形AEBD是矩形。12　例3 如果平行四边形四个内角的平分线能够围成一个四边形，那么这个四边形是矩形．再见