《三角函数》经典专题训练(含答案)2024-2025学年 高中数学 高考专区 真题分类汇编
文档属性
| 名称 | 《三角函数》经典专题训练(含答案)2024-2025学年 高中数学 高考专区 真题分类汇编 |  | |
| 格式 | docx | ||
| 文件大小 | 572.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-17 08:50:13 | ||
图片预览




文档简介
高中数学《三角函数》经典专题训练
(含解析答案)
评卷人 得 分
一.单选题(每题3分,共60分)
1.已知函数y=sin(ωx+φ)(ω>0,|φ|<)的部分图象如图所示,则ω,φ的值分别为( )
A.2,-
B.2,-
C.4,-
D.4,
2.下列说法正确的个数是( )
①小于90°的角是锐角;
②钝角一定大于第一象限角;
③第二象限的角一定大于第一象限的角;
④始边与终边重合的角为0°.
A.0 B.1 C.2 D.3
3.若0<y<x<,且tan2x=3tan(x-y),则x+y的可能取值是( )
A.
B.
C.
D.
4.已知函数y=tan(ωx)(ω>0)的最小正周期为2π,则函数y=ωcosx的值域是( )
A.[-2,2] B.[-1,1] C.[-,] D.[-,]
5.在△ABC中,sin2=(a、b、c分别为角A、B、C的对应边),则△ABC的形状为( )
A.正三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形
6.已知函数f(x)=cosxsin2x,下列结论中错误的是( )
A.f(x)既是偶函数又是周期函数
B.f(x)最大值是1
C.f(x)的图象关于点(,0)对称
D.f(x)的图象关于直线x=π对称
7.sin55°sin65°-cos55°cos65°值为( )
A.
B.
C.-
D.-
8.若角α终边上一点的坐标为(1,-1),则角α为( )
A.2kπ+
B.2kπ-
C.kπ+
D.kπ-,其中k∈Z
9.为了得到函数的图象,只需把函数的图象( )
A.向左平移个单位长度 B.向左平移个单位长度 C.向右平移个单位长度 D.向右平移个单位长度
10.已知α是第二象限的角,那么是第几象限的角( )
A.第一、二象限角 B.第二、三象限角
C.第一、三象限角 D.第三、四象限角
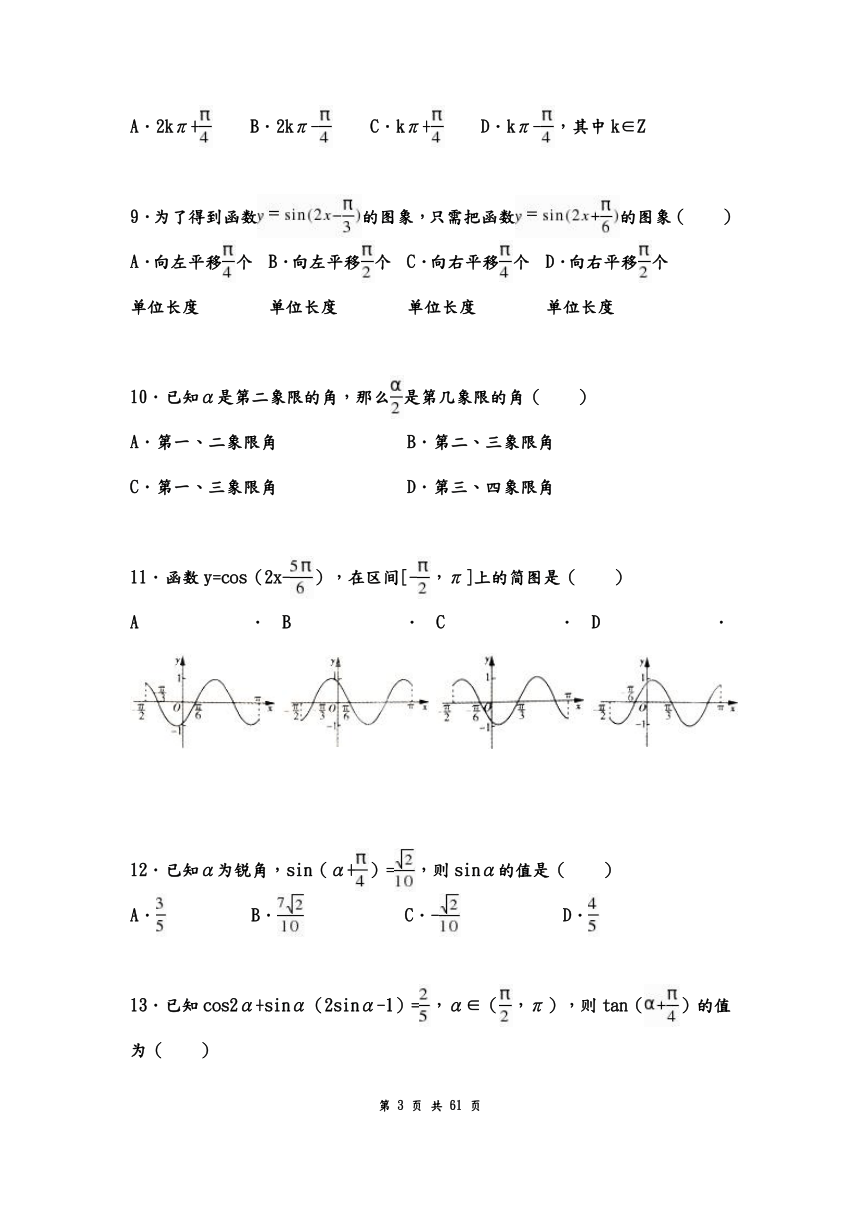
11.函数y=cos(2x-),在区间[-,π]上的简图是( )
A.
B.
C.
D.
12.已知α为锐角,sin(α+)=,则sinα的值是( )
A.
B.
C.-
D.
13.已知cos2α+sinα(2sinα-1)=,α∈(,π),则tan()的值为( )
A.
B.
C.
D.
14.已知m>0,且mcosα-sinα=sin(α+φ),则tanφ=( )
A.-2 B.-
C.
D.2
15.已知cosα+sinα=,则cos(-2α)的值等于( )
A.-
B.-
C.
D.
16.为了得到函数y=3cos2x的图象,只需把函数y=3sin(2x+)的图象上所有的点( )
A.向右平行移动个单位长度 B.向右平行移动个单位长度 C.向左平行移动个单位长度 D.向左平行移动个单位长度
17.若,并且α是第二象限角,那么sinα的值为( )
A.
B.
C.
D.
18.若α是锐角,且cos(α+)=,则sinα的值等于( )
A.
B.
C.
D.
19.若cosα=-,α是第三象限角,则=( )
A.2 B.
C.-2 D.-
20.在△ABC中,若3cos(A-B)+5cosC=0,则tanC的最大值为( )
A.-
B.-
C.-
D.-2
评卷人 得 分
二.填空题(每题3分,共15分)
21.把函数y=3sin(2x+)的图象向右平移个单位长度,再向下平移1个单位长度,则得到的函数的解析式是______.
22.已知π<α+β<π,-π<α-β<-,则2α的取值范围是______.
23.已知α、β均为锐角,且tanβ=,则tan(α+β)=______.
24.已知<β<α<,cos(α-β)=,sin(α+β)=-,则sinα+cosβ=______.
25.sin14°cos16°+cos14°sin16°的值等于______.
评卷人 得 分
三.简答题(每题5分,共25分)
26.函数f(x)=2acos2x+bsinxcosx,满足f(0)=2,f()=+,
(1)求函数f(x)的最大值和最小值;
(2)若α,β∈(0,π),f(α)=f(β),且α≠β,求tan(α+β)的值.
27.已知向量=(-2,sinθ)与=(cosθ,1)互相垂直,其中θ∈(,π).
(1)求sinθ和cosθ的值;
(2)若sin(θ-φ)=,<φ<π,求cosφ的值.
28.已知函数.
(1)求f(x)的最小正周期和对称中心;
(2)若不等式|f(x)-m|≤3对一切x∈[-,]恒成立,求实数m的取值范围;
(3)当x∈[-π,π]时,求f(x)的单调递减区间.
29.已知f(x)=coscos-sinsin.
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)当x∈,求函数f(x)的零点.
30.已知函数(a为常数,x∈R).
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)若函数f(x)在上的最大值与最小值之和为3,求常数a的值.
参考答案
评卷人 得 分
一.单选题(共__小题)
1.已知函数y=sin(ωx+φ)(ω>0,|φ|<)的部分图象如图所示,则ω,φ的值分别为( )
A.2,-
B.2,-
C.4,-
D.4,
答案:A
解析:
解:由图可知,,
∴T=π,
则,
∴ω=2.
又据五点法可得=,解得:φ=-.
故选:A.
2.下列说法正确的个数是( )
①小于90°的角是锐角;
②钝角一定大于第一象限角;
③第二象限的角一定大于第一象限的角;
④始边与终边重合的角为0°.
A.0 B.1 C.2 D.3
答案:A
解析:
解:①-30°是小于90°的角,但它不是锐角,故①错误;
②390°是第一象限的角,故②错误;
③第二象限的角必大于第一象限的角,错误,例如-225°为第二象限的角,30°为第一象限的角,-225°<30°;
④始边与终边重合的角为k 360°,错误;
故选:A.
3.若0<y<x<,且tan2x=3tan(x-y),则x+y的可能取值是( )
A.
B.
C.
D.
答案:A
解析:
解:∵tan2x=3tan(x-y),
∴tan[(x+y)+(x-y)]=3tan(x-y),
由两角和的正切公式可得=3tan(x-y),
变形可得tan(x+y)+tan(x-y)=3tan(x-y)-3tan2(x-y)tan(x+y),
即[1+3tan2(x-y)]tan(x+y)=2tan(x-y),
∴tan(x+y)==,
∵0<y<x<,
∴0<x-y<,
∴tan(x-y)>0,
∴由基本不等式可得tan(x+y)=≤=
当且仅当tan(x-y)=时取等号,
结合0<x+y<π可得x+y≤,或<x+y<π,
四个选项只有A符合,
故选:A
4.已知函数y=tan(ωx)(ω>0)的最小正周期为2π,则函数y=ωcosx的值域是( )
A.[-2,2] B.[-1,1] C.[-,] D.[-,]
答案:D
解析:
解:∵函数y=tan(ωx)(ω>0)的最小正周期为2π,
∴T==2π,
∴ω=.
∴函数y=ωcosx=cosx∈[-,],
∴函数y=cosx的值域是[-,],
故选:D.
5.在△ABC中,sin2=(a、b、c分别为角A、B、C的对应边),则△ABC的形状为( )
A.正三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形
答案:B
解析:
解:因为sin2==,即,由余弦定理可得,
可得a2+b2=c2,所以三角形是直角三角形.
故选B.
6.已知函数f(x)=cosxsin2x,下列结论中错误的是( )
A.f(x)既是偶函数又是周期函数
B.f(x)最大值是1
C.f(x)的图象关于点(,0)对称
D.f(x)的图象关于直线x=π对称
答案:B
解析:
解:A,∵f(x)=cosxsin2x,
∴f(-x)=cos(-x)sin2(-x)=cosxsin2x=f(x),
∴f(x)是偶函数;
又f(x+2π)=cos(x+2π)sin2(x+2π)=cosxsin2x=f(x),
f(x)是周期函数;
∴f(x)既是偶函数又是周期函数,即A正确;
B,∵|cosx|≤1,|sin2x|≤1,二者不能同时取到等号,
∴无论x取什么值,f(x)=cosxsin2x均取不到值1,故B错误;
C,∵f(x)+f(π-x)=cosxsin2x+cos(π-x)sin2(π-x)=cosxsin2x-cosxsin2x=0,
∴f(x)的图象关于点(,0)对称,即C正确;
D,∵f(2π-x)=cos(2π-x)sin2(2π-x)=cosxsin2x=f(x),
∴f(x)的图象关于直线x=π对称,即D正确.
综上所述,结论中错误的是:B.
故选:B.
7.sin55°sin65°-cos55°cos65°值为( )
A.
B.
C.-
D.-
答案:A
解析:
解:sin55°sin65°-cos55°cos65°=-cos(55°+65°)=-cos120°=,
故选:A.
8.若角α终边上一点的坐标为(1,-1),则角α为( )
A.2kπ+
B.2kπ-
C.kπ+
D.kπ-,其中k∈Z
答案:B
解析:
解:终边过点(1,-1),那么可以作出角α的终边,进而得出角α的大小.
所以,α=2kπ-;
故选B.
9.为了得到函数的图象,只需把函数的图象( )
A.向左平移个单位长度 B.向左平移个单位长度 C.向右平移个单位长度 D.向右平移个单位长度
答案:C
解析:
解:∵===
∴把函数的图象向右平移个单位即可得的图象
故选 C
10.已知α是第二象限的角,那么是第几象限的角( )
A.第一、二象限角 B.第二、三象限角
C.第一、三象限角 D.第三、四象限角
答案:C
解析:
解:∵α是第二象限的角,∴2kπ+<α<2kπ+π,k∈z,
∴kπ+<<kπ+,k∈z,故是第一、三象限角,
故选 C.
11.函数y=cos(2x-),在区间[-,π]上的简图是( )
A.
B.
C.
D.
答案:A
解析:
解:∵y=cos(2x-)
=cos(-2x)
=sin[-(-2x)]
=sin(2x-),
又x∈[-,π],
∴2x-∈[-,],
∴当x=-时,y=sin(-π-)
=-sin(π+)
=sin
=>0,故可排除B,D;
又当x=-时,y=sin(2x-)=sin(-π)=0,可排除C,
故选A.
12.已知α为锐角,sin(α+)=,则sinα的值是( )
A.
B.
C.-
D.
答案:D
解析:
解:α为锐角,sin(α+)=<,∴π>α+>.
∴cos(α+)=-=-,
∴sinα=sin[(α+)-]=sin(α+)cos-cos(α+)sin=+=,
故选:D.
13.已知cos2α+sinα(2sinα-1)=,α∈(,π),则tan()的值为( )
A.
B.
C.
D.
答案:A
解析:
解:∵cos2α+sinα(2sinα-1)=,
∴1-2sin2α+2sin2α-sinα=,
解得sinα=,又α∈(,π),
∴cosα==-,
∴tanα==,
∴tan()==
故选:A
14.已知m>0,且mcosα-sinα=sin(α+φ),则tanφ=( )
A.-2 B.-
C.
D.2
答案:A
解析:
解:因为mcosα-sinα=sin(α+φ)=cosφsinα+sinφcosα,
所以,所以m2+1=5,所以m=2,
tanφ=-m=-2.
故选A.
15.已知cosα+sinα=,则cos(-2α)的值等于( )
A.-
B.-
C.
D.
答案:B
解析:
解:∵cosα+sinα=,
∴,∴.
∴cos(-2α)==.
故选:B.
16.为了得到函数y=3cos2x的图象,只需把函数y=3sin(2x+)的图象上所有的点( )
A.向右平行移动个单位长度 B.向右平行移动个单位长度 C.向左平行移动个单位长度 D.向左平行移动个单位长度
答案:D
解析:
解:函数y=3cos2x=3sin(2x+),把函数y=3sin(2x+)的图象上所有的点向左平行移动个单位长度,
可得函数y=3sin[2(x+)+]=3sin(2x+) 的图象,
故选:D.
17.若,并且α是第二象限角,那么sinα的值为( )
A.
B.
C.
D.
答案:D
解析:
解:∵,
∴,
即cosα=-2sinα.
又sin2α+cos2α=1,
∴sin2α+(-2sinα)2=1,
即5sin2α=1.
又α是第二象限角,
∴.
故选:D.
18.若α是锐角,且cos(α+)=,则sinα的值等于( )
A.
B.
C.
D.
答案:B
解析:
解:α是锐角,且cos(α+)=,∴sin(α+)=,
则sinα=sin[(α+)-]=sin(α+)cos-cos(α+)sin=-×=,
故选:B.
19.若cosα=-,α是第三象限角,则=( )
A.2 B.
C.-2 D.-
答案:D
解析:
解:若cosα=-,α是第三象限角,则有 sinα=-.
∴====-,
故选D.
20.在△ABC中,若3cos(A-B)+5cosC=0,则tanC的最大值为( )
A.-
B.-
C.-
D.-2
答案:B
解析:
解:△ABC中,若3cos(A-B)+5cosC=0,即3cos(A-B)+5cos(π-A-B)=3cos(A-B)-5cos(A+B)=0,
即 3cosAcosB+3sinAsinB-5cosAcosB+5sinAsinB=0,
故8sinAsinB=2cosAcosB,tanAtanB=,
tanA+tanB≥2=1,∴tan(A+B)=≥=,
则tanC=-tan(A+B)≤-,当且仅当tanA=tanB时,等号成立,
故选:B.
评卷人 得 分
二.填空题(共__小题)
21.把函数y=3sin(2x+)的图象向右平移个单位长度,再向下平移1个单位长度,则得到的函数的解析式是______.
答案:y=3sin2x-1
解析:
解:把函数y=3sin(2x+)的图象向右平移个单位长度,可得函数y=3sin[2(x-)+]=3sin2x的图象,
再向下平移1个单位长度,则得到的函数的解析式是y=3sin2x-1,
故答案为 y=3sin2x-1.
22.已知π<α+β<π,-π<α-β<-,则2α的取值范围是______.
答案:(0,π)
解析:
解:∵π<α+β<π,-π<α-β<-,
∴0<2α<π,
∴2α的取值范围是(0,π).
故答案为:(0,π).
23.已知α、β均为锐角,且tanβ=,则tan(α+β)=______.
答案:1
解析:
解析:∵tanβ=,
∴tanβ==tan(-α).
又∵α、β均为锐角,∴β=-α,即α+β=,
∴tan(α+β)=tan=1.
故答案为:1.
24.已知<β<α<,cos(α-β)=,sin(α+β)=-,则sinα+cosβ=______.
答案:
解析:
解:∵<β<α<,
∴-<-β<-,
∴π<α+β<,0<α-β<.
又cos(α-β)=,sin(α+β)=-,
∴sin(α-β)==,
cos(α+β)=-,
∴cos[(α-β)+(α+β)]=cos(α-β)cos(α+β)-sin(α-β)sin(α+β)
=×(-)-×(-)
=-.
同理可求:cos[(α+β)-(α-β)]=-;
又α=,β=,
由<β<α<可知,sinα>0,cosβ<0.
∴sinα=sin===,
cosβ=cos=-=-=-,
∴sinα+cosβ==.
故答案为:.
25.sin14°cos16°+cos14°sin16°的值等于______.
答案:
解析:
解:由题意sin14°cos16°+cos14°sin16°=sin30°=
故答案为:.
评卷人 得 分
三.简答题(共__小题)
26.函数f(x)=2acos2x+bsinxcosx,满足f(0)=2,f()=+,
(1)求函数f(x)的最大值和最小值;
(2)若α,β∈(0,π),f(α)=f(β),且α≠β,求tan(α+β)的值.
答案:
解:(1)函数f(x)=2acos2x+bsinxcosx=a(1+cos2x)+,
∵f(0)=2,f()=+,
∴2a=2,+=,
解得a=1,b=2.
∴f(x)=1+cos2x+sin2x
=+1,
∵∈[-1,1],
∴f(x)max=+1,f(x)min=1-.
(2)∵f(α)=f(β),
∴=,
∵α,β∈(0,π),且α≠β,
∴+=π或3π,
∴α+β=或.
∴tan(α+β)=1.
27.已知向量=(-2,sinθ)与=(cosθ,1)互相垂直,其中θ∈(,π).
(1)求sinθ和cosθ的值;
(2)若sin(θ-φ)=,<φ<π,求cosφ的值.
答案:
解:(1)∵与互相垂直,
则,即sinθ=2cosθ,
代入sin2θ+cos2θ=1得,,
又∵θ,∴.
(2)∵φ<π,∴<θ-φ<,
由sin(θ-φ)=,结合同角三角函数关系得
∴cosφ=cos(θ-(θ-φ))=cosθcos(θ-φ)+sinθsin(θ-φ)=.
28.已知函数.
(1)求f(x)的最小正周期和对称中心;
(2)若不等式|f(x)-m|≤3对一切x∈[-,]恒成立,求实数m的取值范围;
(3)当x∈[-π,π]时,求f(x)的单调递减区间.
答案:
解:(1)f(x)=-2sin2x+2sinxcosx+2
=sin2x+cos2x+1
=2sin(2x+)+1,
∴f(x)的最小正周期为T==π.
令2x+=kπ,则x=-(k∈Z),
∴f(x)的对称中心为(-,1)(k∈Z).
(2)∵x∈[-,],
∴-≤2x+≤,
∴-≤sin(2x+)≤1,
∴0≤f(x)≤3.
∴当x=-时,f(x)的最小值为0;
当x=时,f(x)的最大值为3.
由题意得,-3≤f(x)-m≤3,
∴m-3≤f(x)≤m+3对一切x∈[-,]恒成立,
∴,解得0≤m≤3,
∴所求实数m的取值范围为[0,3].
(3)由2kπ+≤2x+≤2kπ+(k∈Z),
得kπ+≤x≤kπ+(k∈Z),
即f(x)的单调递减区间为[kπ+,kπ+](k∈Z),
又x∈[-π,π],
∴f(x)的单调递减区间为[-,-],[,].
29.已知f(x)=coscos-sinsin.
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)当x∈,求函数f(x)的零点.
答案:
解:(Ⅰ)f(x)=coscos-sinsin=cos(+)=cos2x,(4分)
∵ω=2,∴T==π,
则函数f(x)的最小正周期为π;(5分)
(Ⅱ)令f(x)=0,即cos2x=0,
又∵x∈[,π],(7分)
∴2x∈[π,2π],(9分)
∴2x=,即x=,
则x=是函数f(x)的零点.(12分)
30.已知函数(a为常数,x∈R).
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)若函数f(x)在上的最大值与最小值之和为3,求常数a的值.
答案:
解:(Ⅰ)
=
=-2
=,
∴函数f(x)的最小正周期T==π.
(Ⅱ)当x∈,,
∴函数f(x)在上的最大值是,
最小值是,
∴(1+a)+(-2+a)=3,得a=2.
高中数学三角函数(大题)专项训练
1.在△ABC中,角A、B、C对应边a、b、c,外接圆半径为1,已知2(sin2A﹣sin2C)=(a﹣b)sinB.
(1)证明a2+b2﹣c2=ab;
(2)求角C和边c.
2.在△ABC中,内角A,B,C所对的边分别为a,b,c.已知bsinA=acos(B﹣).
(Ⅰ)求角B的大小;
(Ⅱ)设a=2,c=3,求b和sin(2A﹣B)的值.
3.已知α,β为锐角,tanα=,cos(α+β)=﹣.
(1)求cos2α的值;
(2)求tan(α﹣β)的值.
4.在平面四边形ABCD中,∠ADC=90°,∠A=45°,AB=2,BD=5.
(1)求cos∠ADB;
(2)若DC=2,求BC.
5.已知函数f(x)=sin2x+sinxcosx.
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)若f(x)在区间[﹣,m]上的最大值为,求m的最小值.
6.在△ABC中,内角A,B,C所对的边分别为a,b,c.已知asinA=4bsinB,ac=(a2﹣b2﹣c2)
(Ⅰ)求cosA的值;
(Ⅱ)求sin(2B﹣A)的值
7.设函数f(x)=sin(ωx﹣)+sin(ωx﹣),其中0<ω<3,已知f()=0.
(Ⅰ)求ω;
(Ⅱ)将函数y=f(x)的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移个单位,得到函数y=g(x)的图象,求g(x)在[﹣,]上的最小值.
8.在△ABC中,内角A,B,C所对的边分别为a,b,c.已知a>b,a=5,c=6,sinB=.
(Ⅰ)求b和sinA的值;
(Ⅱ)求sin(2A+)的值.
9.△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为.
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周长.
10.△ABC的内角A,B,C的对边分别为a,b,c,已知sin(A+C)=8sin2.
(1)求cosB;
(2)若a+c=6,△ABC的面积为2,求b.
11.已知函数f(x)=cos(2x﹣)﹣2sinxcosx.
(I)求f(x)的最小正周期;
(II)求证:当x∈[﹣,]时,f(x)≥﹣.
12.已知向量=(cosx,sinx),=(3,﹣),x∈[0,π].
(1)若,求x的值;
(2)记f(x)=,求f(x)的最大值和最小值以及对应的x的值.
13.在△ABC中,∠A=60°,c=a.
(1)求sinC的值;
(2)若a=7,求△ABC的面积.
14.已知函数f(x)=2sinωxcosωx+cos2ωx(ω>0)的最小正周期为π.
(1)求ω的值;
(2)求f(x)的单调递增区间.
15.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知b+c=2acosB.
(1)证明:A=2B;
(2)若cosB=,求cosC的值.
16.设f(x)=2sin(π﹣x)sinx﹣(sinx﹣cosx)2.
(Ⅰ)求f(x)的单调递增区间;
(Ⅱ)把y=f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移个单位,得到函数y=g(x)的图象,求g()的值.
17.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知asin2B=bsinA.
(1)求B;
(2)已知cosA=,求sinC的值.
18.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知b+c=2acosB.
(Ⅰ)证明:A=2B;
(Ⅱ)若△ABC的面积S=,求角A的大小.
19.在△ABC中,角A,B,C所对的边分别是a,b,c,且+=.
(Ⅰ)证明:sinAsinB=sinC;
(Ⅱ)若b2+c2﹣a2=bc,求tanB.
20.在△ABC中,AC=6,cosB=,C=.
(1)求AB的长;
(2)求cos(A﹣)的值.
21.已知函数f(x)=4tanxsin(﹣x)cos(x﹣)﹣.
(1)求f(x)的定义域与最小正周期;
(2)讨论f(x)在区间[﹣,]上的单调性.
22.△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.
(Ⅰ)求C;
(Ⅱ)若c=,△ABC的面积为,求△ABC的周长.
参考答案
1.在△ABC中,角A、B、C对应边a、b、c,外接圆半径为1,已知2(sin2A﹣sin2C)=(a﹣b)sinB.
(1)证明a2+b2﹣c2=ab;
(2)求角C和边c.
【解答】证明:(1)∵在△ABC中,角A、B、C对应边a、b、c,外接圆半径为1,
∴由正弦定理得:=2R=2,
∴sinA=,sinB=,sinC=,
∵2(sin2A﹣sin2C)=(a﹣b)sinB,
∴2()=(a﹣b) ,
化简,得:a2+b2﹣c2=ab,
故a2+b2﹣c2=ab.
解:(2)∵a2+b2﹣c2=ab,
∴cosC===,
解得C=,
∴c=2sinC=2 =.
2.在△ABC中,内角A,B,C所对的边分别为a,b,c.已知bsinA=acos(B﹣).
(Ⅰ)求角B的大小;
(Ⅱ)设a=2,c=3,求b和sin(2A﹣B)的值.
【解答】解:(Ⅰ)在△ABC中,由正弦定理得,得bsinA=asinB,
又bsinA=acos(B﹣).
∴asinB=acos(B﹣),即sinB=cos(B﹣)=cosBcos+sinBsin=cosB+,
∴tanB=,
又B∈(0,π),∴B=.
(Ⅱ)在△ABC中,a=2,c=3,B=,
由余弦定理得b==,由bsinA=acos(B﹣),得sinA=,
∵a<c,∴cosA=,
∴sin2A=2sinAcosA=,
cos2A=2cos2A﹣1=,
∴sin(2A﹣B)=sin2AcosB﹣cos2AsinB==.
3.已知α,β为锐角,tanα=,cos(α+β)=﹣.
(1)求cos2α的值;
(2)求tan(α﹣β)的值.
【解答】解:(1)由,解得,
∴cos2α=;
(2)由(1)得,sin2,则tan2α=.
∵α,β∈(0,),∴α+β∈(0,π),
∴sin(α+β)==.
则tan(α+β)=.
∴tan(α﹣β)=tan[2α﹣(α+β)]==.
4.在平面四边形ABCD中,∠ADC=90°,∠A=45°,AB=2,BD=5.
(1)求cos∠ADB;
(2)若DC=2,求BC.
【解答】解:(1)∵∠ADC=90°,∠A=45°,AB=2,BD=5.
∴由正弦定理得:=,即=,
∴sin∠ADB==,
∵AB<BD,∴∠ADB<∠A,
∴cos∠ADB==.
(2)∵∠ADC=90°,∴cos∠BDC=sin∠ADB=,
∵DC=2,
∴BC=
==5.
5.已知函数f(x)=sin2x+sinxcosx.
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)若f(x)在区间[﹣,m]上的最大值为,求m的最小值.
【解答】解:(I)函数f(x)=sin2x+sinxcosx=+sin2x
=sin(2x﹣)+,
f(x)的最小正周期为T==π;
(Ⅱ)若f(x)在区间[﹣,m]上的最大值为,
可得2x﹣∈[﹣,2m﹣],
即有2m﹣≥,解得m≥,
则m的最小值为.
6.在△ABC中,内角A,B,C所对的边分别为a,b,c.已知asinA=4bsinB,ac=(a2﹣b2﹣c2)
(Ⅰ)求cosA的值;
(Ⅱ)求sin(2B﹣A)的值
【解答】(Ⅰ)解:由,得asinB=bsinA,
又asinA=4bsinB,得4bsinB=asinA,
两式作比得:,∴a=2b.
由,得,
由余弦定理,得;
(Ⅱ)解:由(Ⅰ),可得,代入asinA=4bsinB,得.
由(Ⅰ)知,A为钝角,则B为锐角,
∴.
于是,,
故.
7.设函数f(x)=sin(ωx﹣)+sin(ωx﹣),其中0<ω<3,已知f()=0.
(Ⅰ)求ω;
(Ⅱ)将函数y=f(x)的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移个单位,得到函数y=g(x)的图象,求g(x)在[﹣,]上的最小值.
【解答】解:(Ⅰ)函数f(x)=sin(ωx﹣)+sin(ωx﹣)
=sinωxcos﹣cosωxsin﹣sin(﹣ωx)
=sinωx﹣cosωx
=sin(ωx﹣),
又f()=sin(ω﹣)=0,
∴ω﹣=kπ,k∈Z,
解得ω=6k+2,
又0<ω<3,
∴ω=2;
(Ⅱ)由(Ⅰ)知,f(x)=sin(2x﹣),
将函数y=f(x)的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),得到函数y=sin(x﹣)的图象;
再将得到的图象向左平移个单位,得到y=sin(x+﹣)的图象,
∴函数y=g(x)=sin(x﹣);
当x∈[﹣,]时,x﹣∈[﹣,],
∴sin(x﹣)∈[﹣,1],
∴当x=﹣时,g(x)取得最小值是﹣×=﹣.
8.在△ABC中,内角A,B,C所对的边分别为a,b,c.已知a>b,a=5,c=6,sinB=.
(Ⅰ)求b和sinA的值;
(Ⅱ)求sin(2A+)的值.
【解答】解:(Ⅰ)在△ABC中,∵a>b,
故由sinB=,可得cosB=.
由已知及余弦定理,有=13,
∴b=.
由正弦定理,得sinA=.
∴b=,sinA=;
(Ⅱ)由(Ⅰ)及a<c,得cosA=,∴sin2A=2sinAcosA=,
cos2A=1﹣2sin2A=﹣.
故sin(2A+)==.
9.△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为.
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周长.
【解答】解:(1)由三角形的面积公式可得S△ABC=acsinB=,
∴3csinBsinA=2a,
由正弦定理可得3sinCsinBsinA=2sinA,
∵sinA≠0,
∴sinBsinC=;
(2)∵6cosBcosC=1,
∴cosBcosC=,
∴cosBcosC﹣sinBsinC=﹣=﹣,
∴cos(B+C)=﹣,
∴cosA=,
∵0<A<π,
∴A=,
∵===2R==2,
∴sinBsinC= ===,
∴bc=8,
∵a2=b2+c2﹣2bccosA,
∴b2+c2﹣bc=9,
∴(b+c)2=9+3cb=9+24=33,
∴b+c=
∴周长a+b+c=3+.
10.△ABC的内角A,B,C的对边分别为a,b,c,已知sin(A+C)=8sin2.
(1)求cosB;
(2)若a+c=6,△ABC的面积为2,求b.
【解答】解:(1)sin(A+C)=8sin2,
∴sinB=4(1﹣cosB),
∵sin2B+cos2B=1,
∴16(1﹣cosB)2+cos2B=1,
∴16(1﹣cosB)2+cos2B﹣1=0,
∴16(cosB﹣1)2+(cosB﹣1)(cosB+1)=0,
∴(17cosB﹣15)(cosB﹣1)=0,
∴cosB=;
(2)由(1)可知sinB=,
∵S△ABC=ac sinB=2,
∴ac=,
∴b2=a2+c2﹣2accosB=a2+c2﹣2××
=a2+c2﹣15=(a+c)2﹣2ac﹣15=36﹣17﹣15=4,
∴b=2.
11.已知函数f(x)=cos(2x﹣)﹣2sinxcosx.
(I)求f(x)的最小正周期;
(II)求证:当x∈[﹣,]时,f(x)≥﹣.
【解答】解:(Ⅰ)f(x)=cos(2x﹣)﹣2sinxcosx,
=(co2x+sin2x)﹣sin2x,
=cos2x+sin2x,
=sin(2x+),
∴T==π,
∴f(x)的最小正周期为π,
(Ⅱ)∵x∈[﹣,],
∴2x+∈[﹣,],
∴﹣≤sin(2x+)≤1,
∴f(x)≥﹣
12.已知向量=(cosx,sinx),=(3,﹣),x∈[0,π].
(1)若,求x的值;
(2)记f(x)=,求f(x)的最大值和最小值以及对应的x的值.
【解答】解:(1)∵=(cosx,sinx),=(3,﹣),∥,
∴﹣cosx=3sinx,
当cosx=0时,sinx=1,不合题意,
当cosx≠0时,tanx=﹣,
∵x∈[0,π],
∴x=,
(2)f(x)==3cosx﹣sinx=2(cosx﹣sinx)=2cos(x+),
∵x∈[0,π],
∴x+∈[,],
∴﹣1≤cos(x+)≤,
当x=0时,f(x)有最大值,最大值3,
当x=时,f(x)有最小值,最小值﹣2.
13.在△ABC中,∠A=60°,c=a.
(1)求sinC的值;
(2)若a=7,求△ABC的面积.
【解答】解:(1)∠A=60°,c=a,
由正弦定理可得sinC=sinA=×=,
(2)a=7,则c=3,
∴C<A,
∵sin2C+cos2C=1,又由(1)可得cosC=,
∴sinB=sin(A+C)=sinAcosC+cosAsinC=×+×=,
∴S△ABC=acsinB=×7×3×=6.
14.已知函数f(x)=2sinωxcosωx+cos2ωx(ω>0)的最小正周期为π.
(1)求ω的值;
(2)求f(x)的单调递增区间.
【解答】解:f(x)=2sinωxcosωx+cos2ωx,
=sin2ωx+cos2ωx,
=,
由于函数的最小正周期为π,
则:T=,
解得:ω=1.
(2)由(1)得:函数f(x)=,
令(k∈Z),
解得:(k∈Z),
所以函数的单调递增区间为:[](k∈Z).
15.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知b+c=2acosB.
(1)证明:A=2B;
(2)若cosB=,求cosC的值.
【解答】(1)证明:∵b+c=2acosB,
∴sinB+sinC=2sinAcosB,
∵sinC=sin(A+B)=sinAcosB+cosAsinB,
∴sinB=sinAcosB﹣cosAsinB=sin(A﹣B),由A,B∈(0,π),
∴0<A﹣B<π,∴B=A﹣B,或B=π﹣(A﹣B),化为A=2B,或A=π(舍去).
∴A=2B.
(II)解:cosB=,∴sinB==.
cosA=cos2B=2cos2B﹣1=,sinA==.
∴cosC=﹣cos(A+B)=﹣cosAcosB+sinAsinB=+×=.
16.设f(x)=2sin(π﹣x)sinx﹣(sinx﹣cosx)2.
(Ⅰ)求f(x)的单调递增区间;
(Ⅱ)把y=f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移个单位,得到函数y=g(x)的图象,求g()的值.
【解答】解:(Ⅰ)∵f(x)=2sin(π﹣x)sinx﹣(sinx﹣cosx)2 =2sin2x﹣1+sin2x=2 ﹣1+sin2x
=sin2x﹣cos2x+﹣1=2sin(2x﹣)+﹣1,
令2kπ﹣≤2x﹣≤2kπ+,求得kπ﹣≤x≤kπ+,
可得函数的增区间为[kπ﹣,kπ+],k∈Z.
(Ⅱ)把y=f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),可得y=2sin(x﹣)+﹣1的图象;
再把得到的图象向左平移个单位,得到函数y=g(x)=2sinx+﹣1的图象,
∴g()=2sin+﹣1=.
17.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知asin2B=bsinA.
(1)求B;
(2)已知cosA=,求sinC的值.
【解答】解:(1)∵asin2B=bsinA,
∴2sinAsinBcosB=sinBsinA,
∴cosB=,∴B=.
(2)∵cosA=,∴sinA=,
∴sinC=sin(A+B)=sinAcosB+cosAsinB==.
18.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知b+c=2acosB.
(Ⅰ)证明:A=2B;
(Ⅱ)若△ABC的面积S=,求角A的大小.
【解答】(Ⅰ)证明:∵b+c=2acosB,
∴sinB+sinC=2sinAcosB,
∴sinB+sin(A+B)=2sinAcosB
∴sinB+sinAcosB+cosAsinB=2sinAcosB
∴sinB=sinAcosB﹣cosAsinB=sin(A﹣B)
∵A,B是三角形中的角,
∴B=A﹣B,
∴A=2B;
(Ⅱ)解:∵△ABC的面积S=,
∴bcsinA=,
∴2bcsinA=a2,
∴2sinBsinC=sinA=sin2B,
∴sinC=cosB,
∴B+C=90°,或C=B+90°,
∴A=90°或A=45°.
19.在△ABC中,角A,B,C所对的边分别是a,b,c,且+=.
(Ⅰ)证明:sinAsinB=sinC;
(Ⅱ)若b2+c2﹣a2=bc,求tanB.
【解答】(Ⅰ)证明:在△ABC中,∵+=,
∴由正弦定理得:,
∴=,
∵sin(A+B)=sinC.
∴整理可得:sinAsinB=sinC,
(Ⅱ)解:b2+c2﹣a2=bc,由余弦定理可得cosA=.
sinA=,=
+==1,=,
tanB=4.
20.在△ABC中,AC=6,cosB=,C=.
(1)求AB的长;
(2)求cos(A﹣)的值.
【解答】解:(1)∵△ABC中,cosB=,B∈(0,π),
∴sinB=,
∵,
∴AB==5;
(2)cosA═﹣cos(π﹣A)=﹣cos(C+B)=sinBsinC﹣cosBcosC=﹣.
∵A为三角形的内角,
∴sinA=,
∴cos(A﹣)=cosA+sinA=.
21.已知函数f(x)=4tanxsin(﹣x)cos(x﹣)﹣.
(1)求f(x)的定义域与最小正周期;
(2)讨论f(x)在区间[﹣,]上的单调性.
【解答】解:(1)∵f(x)=4tanxsin(﹣x)cos(x﹣)﹣.
∴x≠kπ+,即函数的定义域为{x|x≠kπ+,k∈Z},
则f(x)=4tanxcosx (cosx+sinx)﹣
=4sinx(cosx+sinx)﹣
=2sinxcosx+2sin2x﹣
=sin2x+(1﹣cos2x)﹣
=sin2x﹣cos2x
=2sin(2x﹣),
则函数的周期T=;
(2)由2kπ﹣<2x﹣<2kπ+,k∈Z,
得kπ﹣<x<kπ+,k∈Z,即函数的增区间为(kπ﹣,kπ+),k∈Z,
当k=0时,增区间为(﹣,),k∈Z,
∵x∈[﹣,],∴此时x∈(﹣,],
由2kπ+<2x﹣<2kπ+,k∈Z,
得kπ+<x<kπ+,k∈Z,即函数的减区间为(kπ+,kπ+),k∈Z,
当k=﹣1时,减区间为(﹣,﹣),k∈Z,
∵x∈[﹣,],∴此时x∈[﹣,﹣),
即在区间[﹣,]上,函数的减区间为∈[﹣,﹣),增区间为(﹣,].
22.△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.
(Ⅰ)求C;
(Ⅱ)若c=,△ABC的面积为,求△ABC的周长.
【解答】解:(Ⅰ)∵在△ABC中,0<C<π,∴sinC≠0
已知等式利用正弦定理化简得:2cosC(sinAcosB+sinBcosA)=sinC,
整理得:2cosCsin(A+B)=sinC,
即2cosCsin(π﹣(A+B))=sinC
2cosCsinC=sinC
∴cosC=,
∴C=;
(Ⅱ)由余弦定理得7=a2+b2﹣2ab ,
∴(a+b)2﹣3ab=7,
∵S=absinC=ab=,
∴ab=6,
∴(a+b)2﹣18=7,
∴a+b=5,
∴△ABC的周长为5+.
(含解析答案)
评卷人 得 分
一.单选题(每题3分,共60分)
1.已知函数y=sin(ωx+φ)(ω>0,|φ|<)的部分图象如图所示,则ω,φ的值分别为( )
A.2,-
B.2,-
C.4,-
D.4,
2.下列说法正确的个数是( )
①小于90°的角是锐角;
②钝角一定大于第一象限角;
③第二象限的角一定大于第一象限的角;
④始边与终边重合的角为0°.
A.0 B.1 C.2 D.3
3.若0<y<x<,且tan2x=3tan(x-y),则x+y的可能取值是( )
A.
B.
C.
D.
4.已知函数y=tan(ωx)(ω>0)的最小正周期为2π,则函数y=ωcosx的值域是( )
A.[-2,2] B.[-1,1] C.[-,] D.[-,]
5.在△ABC中,sin2=(a、b、c分别为角A、B、C的对应边),则△ABC的形状为( )
A.正三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形
6.已知函数f(x)=cosxsin2x,下列结论中错误的是( )
A.f(x)既是偶函数又是周期函数
B.f(x)最大值是1
C.f(x)的图象关于点(,0)对称
D.f(x)的图象关于直线x=π对称
7.sin55°sin65°-cos55°cos65°值为( )
A.
B.
C.-
D.-
8.若角α终边上一点的坐标为(1,-1),则角α为( )
A.2kπ+
B.2kπ-
C.kπ+
D.kπ-,其中k∈Z
9.为了得到函数的图象,只需把函数的图象( )
A.向左平移个单位长度 B.向左平移个单位长度 C.向右平移个单位长度 D.向右平移个单位长度
10.已知α是第二象限的角,那么是第几象限的角( )
A.第一、二象限角 B.第二、三象限角
C.第一、三象限角 D.第三、四象限角
11.函数y=cos(2x-),在区间[-,π]上的简图是( )
A.
B.
C.
D.
12.已知α为锐角,sin(α+)=,则sinα的值是( )
A.
B.
C.-
D.
13.已知cos2α+sinα(2sinα-1)=,α∈(,π),则tan()的值为( )
A.
B.
C.
D.
14.已知m>0,且mcosα-sinα=sin(α+φ),则tanφ=( )
A.-2 B.-
C.
D.2
15.已知cosα+sinα=,则cos(-2α)的值等于( )
A.-
B.-
C.
D.
16.为了得到函数y=3cos2x的图象,只需把函数y=3sin(2x+)的图象上所有的点( )
A.向右平行移动个单位长度 B.向右平行移动个单位长度 C.向左平行移动个单位长度 D.向左平行移动个单位长度
17.若,并且α是第二象限角,那么sinα的值为( )
A.
B.
C.
D.
18.若α是锐角,且cos(α+)=,则sinα的值等于( )
A.
B.
C.
D.
19.若cosα=-,α是第三象限角,则=( )
A.2 B.
C.-2 D.-
20.在△ABC中,若3cos(A-B)+5cosC=0,则tanC的最大值为( )
A.-
B.-
C.-
D.-2
评卷人 得 分
二.填空题(每题3分,共15分)
21.把函数y=3sin(2x+)的图象向右平移个单位长度,再向下平移1个单位长度,则得到的函数的解析式是______.
22.已知π<α+β<π,-π<α-β<-,则2α的取值范围是______.
23.已知α、β均为锐角,且tanβ=,则tan(α+β)=______.
24.已知<β<α<,cos(α-β)=,sin(α+β)=-,则sinα+cosβ=______.
25.sin14°cos16°+cos14°sin16°的值等于______.
评卷人 得 分
三.简答题(每题5分,共25分)
26.函数f(x)=2acos2x+bsinxcosx,满足f(0)=2,f()=+,
(1)求函数f(x)的最大值和最小值;
(2)若α,β∈(0,π),f(α)=f(β),且α≠β,求tan(α+β)的值.
27.已知向量=(-2,sinθ)与=(cosθ,1)互相垂直,其中θ∈(,π).
(1)求sinθ和cosθ的值;
(2)若sin(θ-φ)=,<φ<π,求cosφ的值.
28.已知函数.
(1)求f(x)的最小正周期和对称中心;
(2)若不等式|f(x)-m|≤3对一切x∈[-,]恒成立,求实数m的取值范围;
(3)当x∈[-π,π]时,求f(x)的单调递减区间.
29.已知f(x)=coscos-sinsin.
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)当x∈,求函数f(x)的零点.
30.已知函数(a为常数,x∈R).
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)若函数f(x)在上的最大值与最小值之和为3,求常数a的值.
参考答案
评卷人 得 分
一.单选题(共__小题)
1.已知函数y=sin(ωx+φ)(ω>0,|φ|<)的部分图象如图所示,则ω,φ的值分别为( )
A.2,-
B.2,-
C.4,-
D.4,
答案:A
解析:
解:由图可知,,
∴T=π,
则,
∴ω=2.
又据五点法可得=,解得:φ=-.
故选:A.
2.下列说法正确的个数是( )
①小于90°的角是锐角;
②钝角一定大于第一象限角;
③第二象限的角一定大于第一象限的角;
④始边与终边重合的角为0°.
A.0 B.1 C.2 D.3
答案:A
解析:
解:①-30°是小于90°的角,但它不是锐角,故①错误;
②390°是第一象限的角,故②错误;
③第二象限的角必大于第一象限的角,错误,例如-225°为第二象限的角,30°为第一象限的角,-225°<30°;
④始边与终边重合的角为k 360°,错误;
故选:A.
3.若0<y<x<,且tan2x=3tan(x-y),则x+y的可能取值是( )
A.
B.
C.
D.
答案:A
解析:
解:∵tan2x=3tan(x-y),
∴tan[(x+y)+(x-y)]=3tan(x-y),
由两角和的正切公式可得=3tan(x-y),
变形可得tan(x+y)+tan(x-y)=3tan(x-y)-3tan2(x-y)tan(x+y),
即[1+3tan2(x-y)]tan(x+y)=2tan(x-y),
∴tan(x+y)==,
∵0<y<x<,
∴0<x-y<,
∴tan(x-y)>0,
∴由基本不等式可得tan(x+y)=≤=
当且仅当tan(x-y)=时取等号,
结合0<x+y<π可得x+y≤,或<x+y<π,
四个选项只有A符合,
故选:A
4.已知函数y=tan(ωx)(ω>0)的最小正周期为2π,则函数y=ωcosx的值域是( )
A.[-2,2] B.[-1,1] C.[-,] D.[-,]
答案:D
解析:
解:∵函数y=tan(ωx)(ω>0)的最小正周期为2π,
∴T==2π,
∴ω=.
∴函数y=ωcosx=cosx∈[-,],
∴函数y=cosx的值域是[-,],
故选:D.
5.在△ABC中,sin2=(a、b、c分别为角A、B、C的对应边),则△ABC的形状为( )
A.正三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形
答案:B
解析:
解:因为sin2==,即,由余弦定理可得,
可得a2+b2=c2,所以三角形是直角三角形.
故选B.
6.已知函数f(x)=cosxsin2x,下列结论中错误的是( )
A.f(x)既是偶函数又是周期函数
B.f(x)最大值是1
C.f(x)的图象关于点(,0)对称
D.f(x)的图象关于直线x=π对称
答案:B
解析:
解:A,∵f(x)=cosxsin2x,
∴f(-x)=cos(-x)sin2(-x)=cosxsin2x=f(x),
∴f(x)是偶函数;
又f(x+2π)=cos(x+2π)sin2(x+2π)=cosxsin2x=f(x),
f(x)是周期函数;
∴f(x)既是偶函数又是周期函数,即A正确;
B,∵|cosx|≤1,|sin2x|≤1,二者不能同时取到等号,
∴无论x取什么值,f(x)=cosxsin2x均取不到值1,故B错误;
C,∵f(x)+f(π-x)=cosxsin2x+cos(π-x)sin2(π-x)=cosxsin2x-cosxsin2x=0,
∴f(x)的图象关于点(,0)对称,即C正确;
D,∵f(2π-x)=cos(2π-x)sin2(2π-x)=cosxsin2x=f(x),
∴f(x)的图象关于直线x=π对称,即D正确.
综上所述,结论中错误的是:B.
故选:B.
7.sin55°sin65°-cos55°cos65°值为( )
A.
B.
C.-
D.-
答案:A
解析:
解:sin55°sin65°-cos55°cos65°=-cos(55°+65°)=-cos120°=,
故选:A.
8.若角α终边上一点的坐标为(1,-1),则角α为( )
A.2kπ+
B.2kπ-
C.kπ+
D.kπ-,其中k∈Z
答案:B
解析:
解:终边过点(1,-1),那么可以作出角α的终边,进而得出角α的大小.
所以,α=2kπ-;
故选B.
9.为了得到函数的图象,只需把函数的图象( )
A.向左平移个单位长度 B.向左平移个单位长度 C.向右平移个单位长度 D.向右平移个单位长度
答案:C
解析:
解:∵===
∴把函数的图象向右平移个单位即可得的图象
故选 C
10.已知α是第二象限的角,那么是第几象限的角( )
A.第一、二象限角 B.第二、三象限角
C.第一、三象限角 D.第三、四象限角
答案:C
解析:
解:∵α是第二象限的角,∴2kπ+<α<2kπ+π,k∈z,
∴kπ+<<kπ+,k∈z,故是第一、三象限角,
故选 C.
11.函数y=cos(2x-),在区间[-,π]上的简图是( )
A.
B.
C.
D.
答案:A
解析:
解:∵y=cos(2x-)
=cos(-2x)
=sin[-(-2x)]
=sin(2x-),
又x∈[-,π],
∴2x-∈[-,],
∴当x=-时,y=sin(-π-)
=-sin(π+)
=sin
=>0,故可排除B,D;
又当x=-时,y=sin(2x-)=sin(-π)=0,可排除C,
故选A.
12.已知α为锐角,sin(α+)=,则sinα的值是( )
A.
B.
C.-
D.
答案:D
解析:
解:α为锐角,sin(α+)=<,∴π>α+>.
∴cos(α+)=-=-,
∴sinα=sin[(α+)-]=sin(α+)cos-cos(α+)sin=+=,
故选:D.
13.已知cos2α+sinα(2sinα-1)=,α∈(,π),则tan()的值为( )
A.
B.
C.
D.
答案:A
解析:
解:∵cos2α+sinα(2sinα-1)=,
∴1-2sin2α+2sin2α-sinα=,
解得sinα=,又α∈(,π),
∴cosα==-,
∴tanα==,
∴tan()==
故选:A
14.已知m>0,且mcosα-sinα=sin(α+φ),则tanφ=( )
A.-2 B.-
C.
D.2
答案:A
解析:
解:因为mcosα-sinα=sin(α+φ)=cosφsinα+sinφcosα,
所以,所以m2+1=5,所以m=2,
tanφ=-m=-2.
故选A.
15.已知cosα+sinα=,则cos(-2α)的值等于( )
A.-
B.-
C.
D.
答案:B
解析:
解:∵cosα+sinα=,
∴,∴.
∴cos(-2α)==.
故选:B.
16.为了得到函数y=3cos2x的图象,只需把函数y=3sin(2x+)的图象上所有的点( )
A.向右平行移动个单位长度 B.向右平行移动个单位长度 C.向左平行移动个单位长度 D.向左平行移动个单位长度
答案:D
解析:
解:函数y=3cos2x=3sin(2x+),把函数y=3sin(2x+)的图象上所有的点向左平行移动个单位长度,
可得函数y=3sin[2(x+)+]=3sin(2x+) 的图象,
故选:D.
17.若,并且α是第二象限角,那么sinα的值为( )
A.
B.
C.
D.
答案:D
解析:
解:∵,
∴,
即cosα=-2sinα.
又sin2α+cos2α=1,
∴sin2α+(-2sinα)2=1,
即5sin2α=1.
又α是第二象限角,
∴.
故选:D.
18.若α是锐角,且cos(α+)=,则sinα的值等于( )
A.
B.
C.
D.
答案:B
解析:
解:α是锐角,且cos(α+)=,∴sin(α+)=,
则sinα=sin[(α+)-]=sin(α+)cos-cos(α+)sin=-×=,
故选:B.
19.若cosα=-,α是第三象限角,则=( )
A.2 B.
C.-2 D.-
答案:D
解析:
解:若cosα=-,α是第三象限角,则有 sinα=-.
∴====-,
故选D.
20.在△ABC中,若3cos(A-B)+5cosC=0,则tanC的最大值为( )
A.-
B.-
C.-
D.-2
答案:B
解析:
解:△ABC中,若3cos(A-B)+5cosC=0,即3cos(A-B)+5cos(π-A-B)=3cos(A-B)-5cos(A+B)=0,
即 3cosAcosB+3sinAsinB-5cosAcosB+5sinAsinB=0,
故8sinAsinB=2cosAcosB,tanAtanB=,
tanA+tanB≥2=1,∴tan(A+B)=≥=,
则tanC=-tan(A+B)≤-,当且仅当tanA=tanB时,等号成立,
故选:B.
评卷人 得 分
二.填空题(共__小题)
21.把函数y=3sin(2x+)的图象向右平移个单位长度,再向下平移1个单位长度,则得到的函数的解析式是______.
答案:y=3sin2x-1
解析:
解:把函数y=3sin(2x+)的图象向右平移个单位长度,可得函数y=3sin[2(x-)+]=3sin2x的图象,
再向下平移1个单位长度,则得到的函数的解析式是y=3sin2x-1,
故答案为 y=3sin2x-1.
22.已知π<α+β<π,-π<α-β<-,则2α的取值范围是______.
答案:(0,π)
解析:
解:∵π<α+β<π,-π<α-β<-,
∴0<2α<π,
∴2α的取值范围是(0,π).
故答案为:(0,π).
23.已知α、β均为锐角,且tanβ=,则tan(α+β)=______.
答案:1
解析:
解析:∵tanβ=,
∴tanβ==tan(-α).
又∵α、β均为锐角,∴β=-α,即α+β=,
∴tan(α+β)=tan=1.
故答案为:1.
24.已知<β<α<,cos(α-β)=,sin(α+β)=-,则sinα+cosβ=______.
答案:
解析:
解:∵<β<α<,
∴-<-β<-,
∴π<α+β<,0<α-β<.
又cos(α-β)=,sin(α+β)=-,
∴sin(α-β)==,
cos(α+β)=-,
∴cos[(α-β)+(α+β)]=cos(α-β)cos(α+β)-sin(α-β)sin(α+β)
=×(-)-×(-)
=-.
同理可求:cos[(α+β)-(α-β)]=-;
又α=,β=,
由<β<α<可知,sinα>0,cosβ<0.
∴sinα=sin===,
cosβ=cos=-=-=-,
∴sinα+cosβ==.
故答案为:.
25.sin14°cos16°+cos14°sin16°的值等于______.
答案:
解析:
解:由题意sin14°cos16°+cos14°sin16°=sin30°=
故答案为:.
评卷人 得 分
三.简答题(共__小题)
26.函数f(x)=2acos2x+bsinxcosx,满足f(0)=2,f()=+,
(1)求函数f(x)的最大值和最小值;
(2)若α,β∈(0,π),f(α)=f(β),且α≠β,求tan(α+β)的值.
答案:
解:(1)函数f(x)=2acos2x+bsinxcosx=a(1+cos2x)+,
∵f(0)=2,f()=+,
∴2a=2,+=,
解得a=1,b=2.
∴f(x)=1+cos2x+sin2x
=+1,
∵∈[-1,1],
∴f(x)max=+1,f(x)min=1-.
(2)∵f(α)=f(β),
∴=,
∵α,β∈(0,π),且α≠β,
∴+=π或3π,
∴α+β=或.
∴tan(α+β)=1.
27.已知向量=(-2,sinθ)与=(cosθ,1)互相垂直,其中θ∈(,π).
(1)求sinθ和cosθ的值;
(2)若sin(θ-φ)=,<φ<π,求cosφ的值.
答案:
解:(1)∵与互相垂直,
则,即sinθ=2cosθ,
代入sin2θ+cos2θ=1得,,
又∵θ,∴.
(2)∵φ<π,∴<θ-φ<,
由sin(θ-φ)=,结合同角三角函数关系得
∴cosφ=cos(θ-(θ-φ))=cosθcos(θ-φ)+sinθsin(θ-φ)=.
28.已知函数.
(1)求f(x)的最小正周期和对称中心;
(2)若不等式|f(x)-m|≤3对一切x∈[-,]恒成立,求实数m的取值范围;
(3)当x∈[-π,π]时,求f(x)的单调递减区间.
答案:
解:(1)f(x)=-2sin2x+2sinxcosx+2
=sin2x+cos2x+1
=2sin(2x+)+1,
∴f(x)的最小正周期为T==π.
令2x+=kπ,则x=-(k∈Z),
∴f(x)的对称中心为(-,1)(k∈Z).
(2)∵x∈[-,],
∴-≤2x+≤,
∴-≤sin(2x+)≤1,
∴0≤f(x)≤3.
∴当x=-时,f(x)的最小值为0;
当x=时,f(x)的最大值为3.
由题意得,-3≤f(x)-m≤3,
∴m-3≤f(x)≤m+3对一切x∈[-,]恒成立,
∴,解得0≤m≤3,
∴所求实数m的取值范围为[0,3].
(3)由2kπ+≤2x+≤2kπ+(k∈Z),
得kπ+≤x≤kπ+(k∈Z),
即f(x)的单调递减区间为[kπ+,kπ+](k∈Z),
又x∈[-π,π],
∴f(x)的单调递减区间为[-,-],[,].
29.已知f(x)=coscos-sinsin.
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)当x∈,求函数f(x)的零点.
答案:
解:(Ⅰ)f(x)=coscos-sinsin=cos(+)=cos2x,(4分)
∵ω=2,∴T==π,
则函数f(x)的最小正周期为π;(5分)
(Ⅱ)令f(x)=0,即cos2x=0,
又∵x∈[,π],(7分)
∴2x∈[π,2π],(9分)
∴2x=,即x=,
则x=是函数f(x)的零点.(12分)
30.已知函数(a为常数,x∈R).
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)若函数f(x)在上的最大值与最小值之和为3,求常数a的值.
答案:
解:(Ⅰ)
=
=-2
=,
∴函数f(x)的最小正周期T==π.
(Ⅱ)当x∈,,
∴函数f(x)在上的最大值是,
最小值是,
∴(1+a)+(-2+a)=3,得a=2.
高中数学三角函数(大题)专项训练
1.在△ABC中,角A、B、C对应边a、b、c,外接圆半径为1,已知2(sin2A﹣sin2C)=(a﹣b)sinB.
(1)证明a2+b2﹣c2=ab;
(2)求角C和边c.
2.在△ABC中,内角A,B,C所对的边分别为a,b,c.已知bsinA=acos(B﹣).
(Ⅰ)求角B的大小;
(Ⅱ)设a=2,c=3,求b和sin(2A﹣B)的值.
3.已知α,β为锐角,tanα=,cos(α+β)=﹣.
(1)求cos2α的值;
(2)求tan(α﹣β)的值.
4.在平面四边形ABCD中,∠ADC=90°,∠A=45°,AB=2,BD=5.
(1)求cos∠ADB;
(2)若DC=2,求BC.
5.已知函数f(x)=sin2x+sinxcosx.
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)若f(x)在区间[﹣,m]上的最大值为,求m的最小值.
6.在△ABC中,内角A,B,C所对的边分别为a,b,c.已知asinA=4bsinB,ac=(a2﹣b2﹣c2)
(Ⅰ)求cosA的值;
(Ⅱ)求sin(2B﹣A)的值
7.设函数f(x)=sin(ωx﹣)+sin(ωx﹣),其中0<ω<3,已知f()=0.
(Ⅰ)求ω;
(Ⅱ)将函数y=f(x)的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移个单位,得到函数y=g(x)的图象,求g(x)在[﹣,]上的最小值.
8.在△ABC中,内角A,B,C所对的边分别为a,b,c.已知a>b,a=5,c=6,sinB=.
(Ⅰ)求b和sinA的值;
(Ⅱ)求sin(2A+)的值.
9.△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为.
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周长.
10.△ABC的内角A,B,C的对边分别为a,b,c,已知sin(A+C)=8sin2.
(1)求cosB;
(2)若a+c=6,△ABC的面积为2,求b.
11.已知函数f(x)=cos(2x﹣)﹣2sinxcosx.
(I)求f(x)的最小正周期;
(II)求证:当x∈[﹣,]时,f(x)≥﹣.
12.已知向量=(cosx,sinx),=(3,﹣),x∈[0,π].
(1)若,求x的值;
(2)记f(x)=,求f(x)的最大值和最小值以及对应的x的值.
13.在△ABC中,∠A=60°,c=a.
(1)求sinC的值;
(2)若a=7,求△ABC的面积.
14.已知函数f(x)=2sinωxcosωx+cos2ωx(ω>0)的最小正周期为π.
(1)求ω的值;
(2)求f(x)的单调递增区间.
15.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知b+c=2acosB.
(1)证明:A=2B;
(2)若cosB=,求cosC的值.
16.设f(x)=2sin(π﹣x)sinx﹣(sinx﹣cosx)2.
(Ⅰ)求f(x)的单调递增区间;
(Ⅱ)把y=f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移个单位,得到函数y=g(x)的图象,求g()的值.
17.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知asin2B=bsinA.
(1)求B;
(2)已知cosA=,求sinC的值.
18.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知b+c=2acosB.
(Ⅰ)证明:A=2B;
(Ⅱ)若△ABC的面积S=,求角A的大小.
19.在△ABC中,角A,B,C所对的边分别是a,b,c,且+=.
(Ⅰ)证明:sinAsinB=sinC;
(Ⅱ)若b2+c2﹣a2=bc,求tanB.
20.在△ABC中,AC=6,cosB=,C=.
(1)求AB的长;
(2)求cos(A﹣)的值.
21.已知函数f(x)=4tanxsin(﹣x)cos(x﹣)﹣.
(1)求f(x)的定义域与最小正周期;
(2)讨论f(x)在区间[﹣,]上的单调性.
22.△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.
(Ⅰ)求C;
(Ⅱ)若c=,△ABC的面积为,求△ABC的周长.
参考答案
1.在△ABC中,角A、B、C对应边a、b、c,外接圆半径为1,已知2(sin2A﹣sin2C)=(a﹣b)sinB.
(1)证明a2+b2﹣c2=ab;
(2)求角C和边c.
【解答】证明:(1)∵在△ABC中,角A、B、C对应边a、b、c,外接圆半径为1,
∴由正弦定理得:=2R=2,
∴sinA=,sinB=,sinC=,
∵2(sin2A﹣sin2C)=(a﹣b)sinB,
∴2()=(a﹣b) ,
化简,得:a2+b2﹣c2=ab,
故a2+b2﹣c2=ab.
解:(2)∵a2+b2﹣c2=ab,
∴cosC===,
解得C=,
∴c=2sinC=2 =.
2.在△ABC中,内角A,B,C所对的边分别为a,b,c.已知bsinA=acos(B﹣).
(Ⅰ)求角B的大小;
(Ⅱ)设a=2,c=3,求b和sin(2A﹣B)的值.
【解答】解:(Ⅰ)在△ABC中,由正弦定理得,得bsinA=asinB,
又bsinA=acos(B﹣).
∴asinB=acos(B﹣),即sinB=cos(B﹣)=cosBcos+sinBsin=cosB+,
∴tanB=,
又B∈(0,π),∴B=.
(Ⅱ)在△ABC中,a=2,c=3,B=,
由余弦定理得b==,由bsinA=acos(B﹣),得sinA=,
∵a<c,∴cosA=,
∴sin2A=2sinAcosA=,
cos2A=2cos2A﹣1=,
∴sin(2A﹣B)=sin2AcosB﹣cos2AsinB==.
3.已知α,β为锐角,tanα=,cos(α+β)=﹣.
(1)求cos2α的值;
(2)求tan(α﹣β)的值.
【解答】解:(1)由,解得,
∴cos2α=;
(2)由(1)得,sin2,则tan2α=.
∵α,β∈(0,),∴α+β∈(0,π),
∴sin(α+β)==.
则tan(α+β)=.
∴tan(α﹣β)=tan[2α﹣(α+β)]==.
4.在平面四边形ABCD中,∠ADC=90°,∠A=45°,AB=2,BD=5.
(1)求cos∠ADB;
(2)若DC=2,求BC.
【解答】解:(1)∵∠ADC=90°,∠A=45°,AB=2,BD=5.
∴由正弦定理得:=,即=,
∴sin∠ADB==,
∵AB<BD,∴∠ADB<∠A,
∴cos∠ADB==.
(2)∵∠ADC=90°,∴cos∠BDC=sin∠ADB=,
∵DC=2,
∴BC=
==5.
5.已知函数f(x)=sin2x+sinxcosx.
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)若f(x)在区间[﹣,m]上的最大值为,求m的最小值.
【解答】解:(I)函数f(x)=sin2x+sinxcosx=+sin2x
=sin(2x﹣)+,
f(x)的最小正周期为T==π;
(Ⅱ)若f(x)在区间[﹣,m]上的最大值为,
可得2x﹣∈[﹣,2m﹣],
即有2m﹣≥,解得m≥,
则m的最小值为.
6.在△ABC中,内角A,B,C所对的边分别为a,b,c.已知asinA=4bsinB,ac=(a2﹣b2﹣c2)
(Ⅰ)求cosA的值;
(Ⅱ)求sin(2B﹣A)的值
【解答】(Ⅰ)解:由,得asinB=bsinA,
又asinA=4bsinB,得4bsinB=asinA,
两式作比得:,∴a=2b.
由,得,
由余弦定理,得;
(Ⅱ)解:由(Ⅰ),可得,代入asinA=4bsinB,得.
由(Ⅰ)知,A为钝角,则B为锐角,
∴.
于是,,
故.
7.设函数f(x)=sin(ωx﹣)+sin(ωx﹣),其中0<ω<3,已知f()=0.
(Ⅰ)求ω;
(Ⅱ)将函数y=f(x)的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移个单位,得到函数y=g(x)的图象,求g(x)在[﹣,]上的最小值.
【解答】解:(Ⅰ)函数f(x)=sin(ωx﹣)+sin(ωx﹣)
=sinωxcos﹣cosωxsin﹣sin(﹣ωx)
=sinωx﹣cosωx
=sin(ωx﹣),
又f()=sin(ω﹣)=0,
∴ω﹣=kπ,k∈Z,
解得ω=6k+2,
又0<ω<3,
∴ω=2;
(Ⅱ)由(Ⅰ)知,f(x)=sin(2x﹣),
将函数y=f(x)的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),得到函数y=sin(x﹣)的图象;
再将得到的图象向左平移个单位,得到y=sin(x+﹣)的图象,
∴函数y=g(x)=sin(x﹣);
当x∈[﹣,]时,x﹣∈[﹣,],
∴sin(x﹣)∈[﹣,1],
∴当x=﹣时,g(x)取得最小值是﹣×=﹣.
8.在△ABC中,内角A,B,C所对的边分别为a,b,c.已知a>b,a=5,c=6,sinB=.
(Ⅰ)求b和sinA的值;
(Ⅱ)求sin(2A+)的值.
【解答】解:(Ⅰ)在△ABC中,∵a>b,
故由sinB=,可得cosB=.
由已知及余弦定理,有=13,
∴b=.
由正弦定理,得sinA=.
∴b=,sinA=;
(Ⅱ)由(Ⅰ)及a<c,得cosA=,∴sin2A=2sinAcosA=,
cos2A=1﹣2sin2A=﹣.
故sin(2A+)==.
9.△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为.
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周长.
【解答】解:(1)由三角形的面积公式可得S△ABC=acsinB=,
∴3csinBsinA=2a,
由正弦定理可得3sinCsinBsinA=2sinA,
∵sinA≠0,
∴sinBsinC=;
(2)∵6cosBcosC=1,
∴cosBcosC=,
∴cosBcosC﹣sinBsinC=﹣=﹣,
∴cos(B+C)=﹣,
∴cosA=,
∵0<A<π,
∴A=,
∵===2R==2,
∴sinBsinC= ===,
∴bc=8,
∵a2=b2+c2﹣2bccosA,
∴b2+c2﹣bc=9,
∴(b+c)2=9+3cb=9+24=33,
∴b+c=
∴周长a+b+c=3+.
10.△ABC的内角A,B,C的对边分别为a,b,c,已知sin(A+C)=8sin2.
(1)求cosB;
(2)若a+c=6,△ABC的面积为2,求b.
【解答】解:(1)sin(A+C)=8sin2,
∴sinB=4(1﹣cosB),
∵sin2B+cos2B=1,
∴16(1﹣cosB)2+cos2B=1,
∴16(1﹣cosB)2+cos2B﹣1=0,
∴16(cosB﹣1)2+(cosB﹣1)(cosB+1)=0,
∴(17cosB﹣15)(cosB﹣1)=0,
∴cosB=;
(2)由(1)可知sinB=,
∵S△ABC=ac sinB=2,
∴ac=,
∴b2=a2+c2﹣2accosB=a2+c2﹣2××
=a2+c2﹣15=(a+c)2﹣2ac﹣15=36﹣17﹣15=4,
∴b=2.
11.已知函数f(x)=cos(2x﹣)﹣2sinxcosx.
(I)求f(x)的最小正周期;
(II)求证:当x∈[﹣,]时,f(x)≥﹣.
【解答】解:(Ⅰ)f(x)=cos(2x﹣)﹣2sinxcosx,
=(co2x+sin2x)﹣sin2x,
=cos2x+sin2x,
=sin(2x+),
∴T==π,
∴f(x)的最小正周期为π,
(Ⅱ)∵x∈[﹣,],
∴2x+∈[﹣,],
∴﹣≤sin(2x+)≤1,
∴f(x)≥﹣
12.已知向量=(cosx,sinx),=(3,﹣),x∈[0,π].
(1)若,求x的值;
(2)记f(x)=,求f(x)的最大值和最小值以及对应的x的值.
【解答】解:(1)∵=(cosx,sinx),=(3,﹣),∥,
∴﹣cosx=3sinx,
当cosx=0时,sinx=1,不合题意,
当cosx≠0时,tanx=﹣,
∵x∈[0,π],
∴x=,
(2)f(x)==3cosx﹣sinx=2(cosx﹣sinx)=2cos(x+),
∵x∈[0,π],
∴x+∈[,],
∴﹣1≤cos(x+)≤,
当x=0时,f(x)有最大值,最大值3,
当x=时,f(x)有最小值,最小值﹣2.
13.在△ABC中,∠A=60°,c=a.
(1)求sinC的值;
(2)若a=7,求△ABC的面积.
【解答】解:(1)∠A=60°,c=a,
由正弦定理可得sinC=sinA=×=,
(2)a=7,则c=3,
∴C<A,
∵sin2C+cos2C=1,又由(1)可得cosC=,
∴sinB=sin(A+C)=sinAcosC+cosAsinC=×+×=,
∴S△ABC=acsinB=×7×3×=6.
14.已知函数f(x)=2sinωxcosωx+cos2ωx(ω>0)的最小正周期为π.
(1)求ω的值;
(2)求f(x)的单调递增区间.
【解答】解:f(x)=2sinωxcosωx+cos2ωx,
=sin2ωx+cos2ωx,
=,
由于函数的最小正周期为π,
则:T=,
解得:ω=1.
(2)由(1)得:函数f(x)=,
令(k∈Z),
解得:(k∈Z),
所以函数的单调递增区间为:[](k∈Z).
15.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知b+c=2acosB.
(1)证明:A=2B;
(2)若cosB=,求cosC的值.
【解答】(1)证明:∵b+c=2acosB,
∴sinB+sinC=2sinAcosB,
∵sinC=sin(A+B)=sinAcosB+cosAsinB,
∴sinB=sinAcosB﹣cosAsinB=sin(A﹣B),由A,B∈(0,π),
∴0<A﹣B<π,∴B=A﹣B,或B=π﹣(A﹣B),化为A=2B,或A=π(舍去).
∴A=2B.
(II)解:cosB=,∴sinB==.
cosA=cos2B=2cos2B﹣1=,sinA==.
∴cosC=﹣cos(A+B)=﹣cosAcosB+sinAsinB=+×=.
16.设f(x)=2sin(π﹣x)sinx﹣(sinx﹣cosx)2.
(Ⅰ)求f(x)的单调递增区间;
(Ⅱ)把y=f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移个单位,得到函数y=g(x)的图象,求g()的值.
【解答】解:(Ⅰ)∵f(x)=2sin(π﹣x)sinx﹣(sinx﹣cosx)2 =2sin2x﹣1+sin2x=2 ﹣1+sin2x
=sin2x﹣cos2x+﹣1=2sin(2x﹣)+﹣1,
令2kπ﹣≤2x﹣≤2kπ+,求得kπ﹣≤x≤kπ+,
可得函数的增区间为[kπ﹣,kπ+],k∈Z.
(Ⅱ)把y=f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),可得y=2sin(x﹣)+﹣1的图象;
再把得到的图象向左平移个单位,得到函数y=g(x)=2sinx+﹣1的图象,
∴g()=2sin+﹣1=.
17.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知asin2B=bsinA.
(1)求B;
(2)已知cosA=,求sinC的值.
【解答】解:(1)∵asin2B=bsinA,
∴2sinAsinBcosB=sinBsinA,
∴cosB=,∴B=.
(2)∵cosA=,∴sinA=,
∴sinC=sin(A+B)=sinAcosB+cosAsinB==.
18.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知b+c=2acosB.
(Ⅰ)证明:A=2B;
(Ⅱ)若△ABC的面积S=,求角A的大小.
【解答】(Ⅰ)证明:∵b+c=2acosB,
∴sinB+sinC=2sinAcosB,
∴sinB+sin(A+B)=2sinAcosB
∴sinB+sinAcosB+cosAsinB=2sinAcosB
∴sinB=sinAcosB﹣cosAsinB=sin(A﹣B)
∵A,B是三角形中的角,
∴B=A﹣B,
∴A=2B;
(Ⅱ)解:∵△ABC的面积S=,
∴bcsinA=,
∴2bcsinA=a2,
∴2sinBsinC=sinA=sin2B,
∴sinC=cosB,
∴B+C=90°,或C=B+90°,
∴A=90°或A=45°.
19.在△ABC中,角A,B,C所对的边分别是a,b,c,且+=.
(Ⅰ)证明:sinAsinB=sinC;
(Ⅱ)若b2+c2﹣a2=bc,求tanB.
【解答】(Ⅰ)证明:在△ABC中,∵+=,
∴由正弦定理得:,
∴=,
∵sin(A+B)=sinC.
∴整理可得:sinAsinB=sinC,
(Ⅱ)解:b2+c2﹣a2=bc,由余弦定理可得cosA=.
sinA=,=
+==1,=,
tanB=4.
20.在△ABC中,AC=6,cosB=,C=.
(1)求AB的长;
(2)求cos(A﹣)的值.
【解答】解:(1)∵△ABC中,cosB=,B∈(0,π),
∴sinB=,
∵,
∴AB==5;
(2)cosA═﹣cos(π﹣A)=﹣cos(C+B)=sinBsinC﹣cosBcosC=﹣.
∵A为三角形的内角,
∴sinA=,
∴cos(A﹣)=cosA+sinA=.
21.已知函数f(x)=4tanxsin(﹣x)cos(x﹣)﹣.
(1)求f(x)的定义域与最小正周期;
(2)讨论f(x)在区间[﹣,]上的单调性.
【解答】解:(1)∵f(x)=4tanxsin(﹣x)cos(x﹣)﹣.
∴x≠kπ+,即函数的定义域为{x|x≠kπ+,k∈Z},
则f(x)=4tanxcosx (cosx+sinx)﹣
=4sinx(cosx+sinx)﹣
=2sinxcosx+2sin2x﹣
=sin2x+(1﹣cos2x)﹣
=sin2x﹣cos2x
=2sin(2x﹣),
则函数的周期T=;
(2)由2kπ﹣<2x﹣<2kπ+,k∈Z,
得kπ﹣<x<kπ+,k∈Z,即函数的增区间为(kπ﹣,kπ+),k∈Z,
当k=0时,增区间为(﹣,),k∈Z,
∵x∈[﹣,],∴此时x∈(﹣,],
由2kπ+<2x﹣<2kπ+,k∈Z,
得kπ+<x<kπ+,k∈Z,即函数的减区间为(kπ+,kπ+),k∈Z,
当k=﹣1时,减区间为(﹣,﹣),k∈Z,
∵x∈[﹣,],∴此时x∈[﹣,﹣),
即在区间[﹣,]上,函数的减区间为∈[﹣,﹣),增区间为(﹣,].
22.△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.
(Ⅰ)求C;
(Ⅱ)若c=,△ABC的面积为,求△ABC的周长.
【解答】解:(Ⅰ)∵在△ABC中,0<C<π,∴sinC≠0
已知等式利用正弦定理化简得:2cosC(sinAcosB+sinBcosA)=sinC,
整理得:2cosCsin(A+B)=sinC,
即2cosCsin(π﹣(A+B))=sinC
2cosCsinC=sinC
∴cosC=,
∴C=;
(Ⅱ)由余弦定理得7=a2+b2﹣2ab ,
∴(a+b)2﹣3ab=7,
∵S=absinC=ab=,
∴ab=6,
∴(a+b)2﹣18=7,
∴a+b=5,
∴△ABC的周长为5+.
同课章节目录
