1.3反比例函数的应用课件

课件12张PPT。反比例函数的应用1.反比例函数的一般形式:2.反比例函数的图象:3.反比例函数的图象的特征:双曲线(1)k＞0时,双曲线位于一,三象限,在每一象限内,y 随x的增大而减小;(2) k＜0时,双曲线位于二,四象限,在每一象限内,y 随x的增大而增大; 知识回顾某科技小组在一次野外考察图中遇到一片烂泥湿地，为了安
全、迅速地通过这片湿地，他们沿着前进路线铺垫了若干块
木板，构成一条临时通道，从而顺利通过了这片湿地。思考探究
(1)根据压力F(N)、压强p(Pa)与受力面积S(m2)之间
的关系式 ，请你判断：当F一定时，p是S的
反比例函数吗？
对于 ，当F一定时，根据反比例函数的定义可
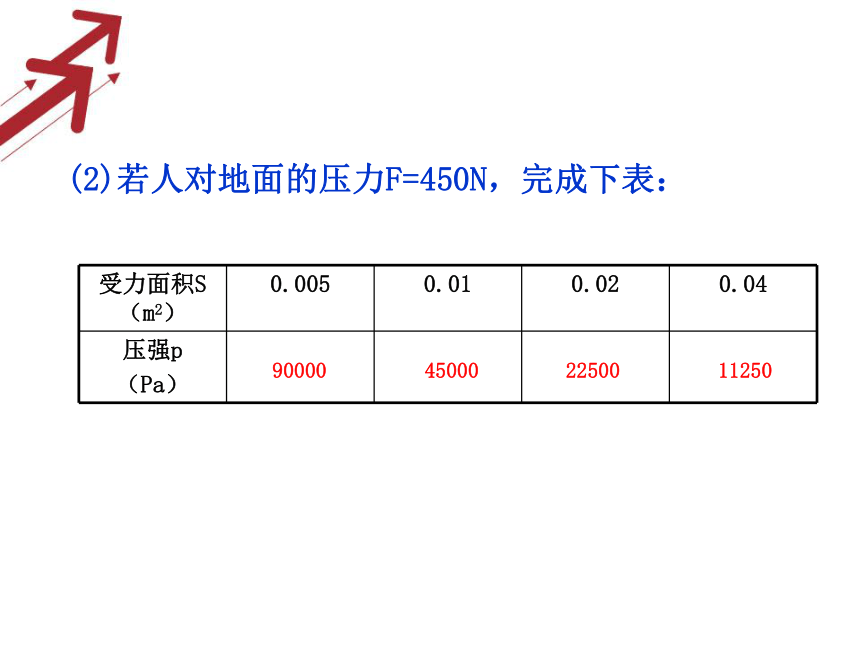
知，p是S 的反比例函数。(2)若人对地面的压力F=450N，完成下表：
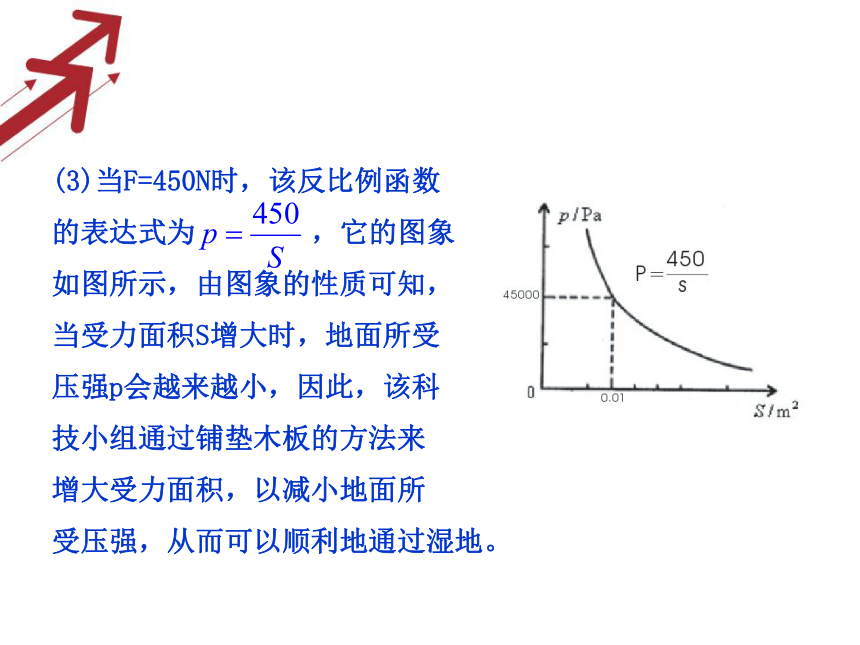
90000 45000 22500 11250 (3)当F=450N时，该反比例函数
的表达式为 ，它的图象
如图所示，由图象的性质可知，
当受力面积S增大时，地面所受
压强p会越来越小，因此，该科
技小组通过铺垫木板的方法来
增大受力面积，以减小地面所
受压强，从而可以顺利地通过湿地。
1、蓄电池的电压为定值，使用此电源时，电流I(A)与电阻
R(Ω)之间的函数关系如图所示。
(1)蓄电池的电压是多少？
你能写出这一函数的表达式吗？

解：（1）U=I×R=9×4=36 V；
I=
能力提升36R(2)如果以此蓄电池为电源的用电器限制电流不得超
过10A，那么用电器的可变电阻应控制在什么范
围内？
解：I≤10即 ≤10，

从而解得：R≥3.6 Ω36R2、如图，正比例函数y＝k1x的图象与反比例函数
的图象相交于A，B两点，其中点A的坐标为(√3,2√3).
(1)分别写出这两个函数的表达式；
(2)你能求出点B的坐标吗?
解：（1）y=2x，y=
（2）B（-√3，-2√3）x6用反比例函数解决实际问题的步骤是:1.认真分析实际问题中变量之间的关系;2.若具有反比例关系,则建立反比例函数模型
(其实是解析式,也叫建模);3.利用反比例函数的有关知识解决实际问题.小结
通过本节课的学习你有哪些收获，
还有哪些疑惑？ 课堂总结完成状元导练本课时的习题。课后作业