12.3 角的平分线的性质 同步测试卷(含简单答案)2024-2025学年人教版八年级数学上册
文档属性
| 名称 | 12.3 角的平分线的性质 同步测试卷(含简单答案)2024-2025学年人教版八年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 508.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-18 11:29:31 | ||
图片预览




文档简介
12.3 角的平分线的性质 同步测试卷2024-2025学年人教版八年级数学上册
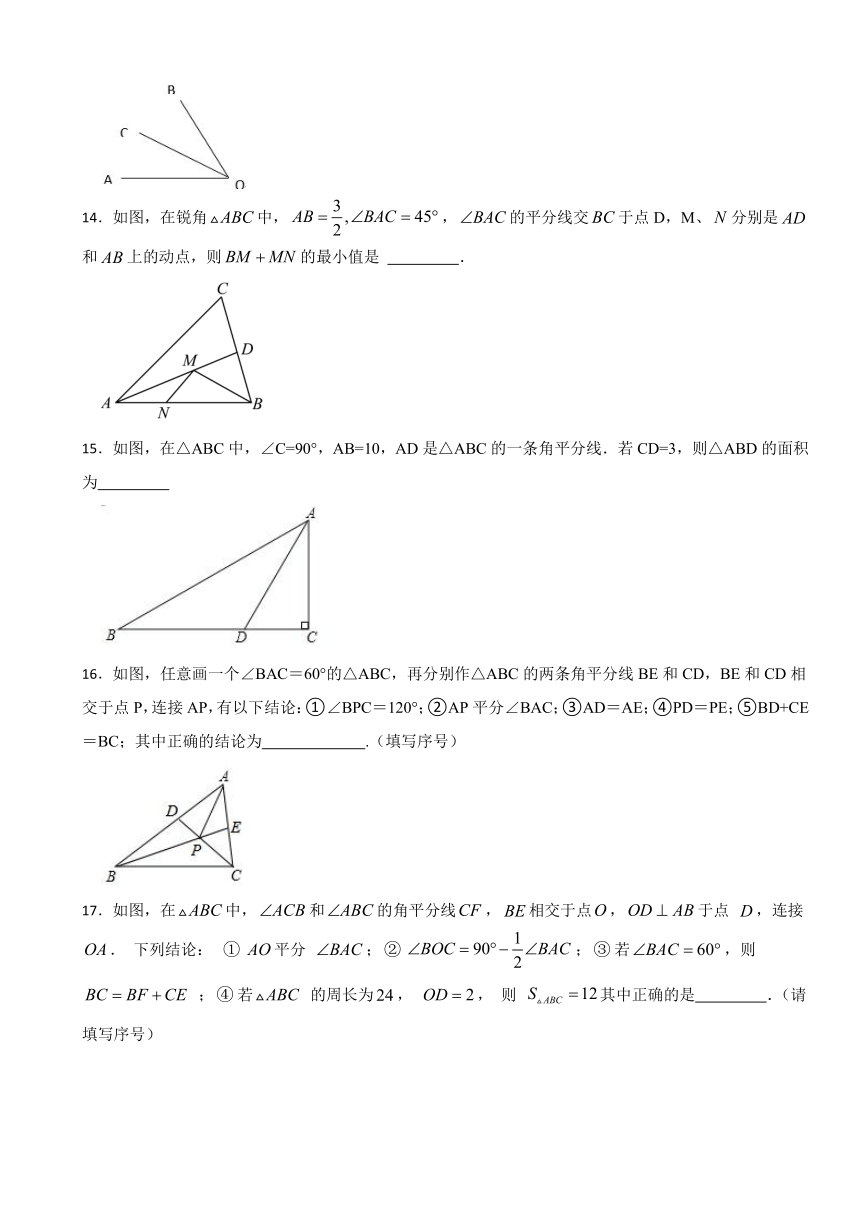
一、单选题
1.如图,平分,点P射线上一点,于点M,点N射线OA上的一个动点,若,则的长度不可能是( )
A.3 B.4 C.5 D.6
2.如图,在中,的平分线交于点是中点,且,那么的度数为( )
A. B. C. D.
3.如图,直线AB、CD相交于点O,射线OM平分∠AOC,ON⊥OM.若∠BOD=70°,则∠CON的度数为( )
A.35° B.45° C.55° D.65°
4.已知和射线MN.如图,以点为圆心,任意长度为半径画弧分别交的两边于点P,Q,接着在射线MN上以点为圆心,OP长为半径画弧交射线MN于点;以为圆心,PQ长为半径画两段弧,分别交于C,D两点,连结MC,MD并延长.则的度数为( )
A. B. C. D.
5.如图,在△ABC中,∠C=90°,AC=BC,AD是∠CAB的角平分线,DE⊥AB于点E,若AB=6cm,则△DEB的周长是( )
A.5cm B.6cm C.7cm D.8cm
6.如图,在四边形中,,平分,,则的面积是( )
A.6 B.8 C.10 D.12
7.如图,△ABC中,∠ABC、∠EAC的角平分线BP、AP交于点P,延长BA、BC,PM⊥BE,PN⊥BF,则下列结论中正确的个数( )
①CP平分∠ACF;②∠ABC+2∠APC=180°;③∠ACB=2∠APB;④S△PAC=S△MAP+S△NCP.
A.1个 B.2个 C.3个 D.4个
8.如图,点E在CA延长线上,DE,AB交于点F,且∠BDE=∠AEF,∠B=∠C,∠EFA比∠FDC的余角小10°,P为线段DC上一动点,Q为PC上一点,且满足∠FQP=∠QFP,FM为∠EFP的平分线.下列结论:①CEBD;②ABCD;③FQ平分∠AFP;④∠B+∠E=140°;⑤∠QFM=20°.其中结论正确的序号是( )
A.①②③④⑤ B.①②③④ C.②③④ D.①⑤
9.如图,在中,,的外角平分线与内角平分线的延长线交于点,过点作交延长线于点,连接,点为中点.有下列结论:①;②;③;④.其中正确的是( )
A.①② B.③④ C.①②③ D.①②④
二、填空题
10.如图,直线交于点,平分,若,则 .
11.如图,的角平分线、交于点.延长至,与的延长线相交于点,且,,若的面积为6,,则线段的长度为 .
12.如图,在△ABC中,AD平分∠BAC,DE⊥AB于点E,S△ABC=15,DE=3,AB=6,则AC长是 .
13.如图:已知∠AOB=60°,OC平分∠A0B,在同一平面内以O为端点画射线OD,使∠COD=10°,则∠AOD= .
14.如图,在锐角中,,的平分线交于点D,M、分别是和上的动点,则的最小值是 .
15.如图,在△ABC中,∠C=90°,AB=10,AD是△ABC的一条角平分线.若CD=3,则△ABD的面积为
16.如图,任意画一个∠BAC=60°的△ABC,再分别作△ABC的两条角平分线BE和CD,BE和CD相交于点P,连接AP,有以下结论:①∠BPC=120°;②AP平分∠BAC;③AD=AE;④PD=PE;⑤BD+CE=BC;其中正确的结论为 .(填写序号)
17.如图,在中,和的角平分线,相交于点,于点 ,连接. 下列结论: 平分 ;;若,则 ;若 的周长为, , 则 其中正确的是 .(请填写序号)
三、解答题
18.如图,在中,,,于D,平分交于E,于F,求的度数.
19.如图所示,在中,为的角平分线,于E,于F,的面积是,,,求的长.
20.综合与探究
特例感知:(1)如图1,线段,为线段上的一个动点,点,分别是,的中点.
①若,则线段的长为___________;
②设,则线段的长为___________.
知识迁移:
(2)我们发现角的很多规律和线段一样,如图2,若,是内部的一条射线,射线平分,射线平分,求的度数.
拓展探究:
(3)已知在内的位置如图3所示,若,且,,求与的数量关系.
21.如图所示,在中,平分 ,是高线, ,,求的度数.
22.如图,已知BE平分∠ABC,点D在射线BA上,且∠ABE=∠BED,若∠ABE=25°时,求∠ADE的度数.
23.如图,直线和相交于点O,,平分.
(1)若,求的度数:
(2)若比小,求的度数.
24.已知:.
(1)如图1,若.
①写出图中一组相等的角(除直角外) ,理由是 .
②那么 .
(2)如图2,与重合,若,将绕点以5度秒的速度作逆时针旋转,运动时间为秒.
①当 秒时,平分;
②试说明:当为何值时,?
答案解析部分
1.【答案】A
2.【答案】C
3.【答案】C
4.【答案】D
5.【答案】B
6.【答案】A
7.【答案】D
8.【答案】A
9.【答案】D
10.【答案】
11.【答案】
12.【答案】4
13.【答案】20°或40°
14.【答案】
15.【答案】15
16.【答案】①②④⑤
17.【答案】
18.【答案】
19.【答案】
20.【答案】(1)①8;②;(2);(3)
21.【答案】解:∵平分 ,是高线,,
∴,,
∴,
∴,
∴的度数为.
22.【答案】解:∵BE平分∠ABC,
∴∠ABE=∠EBC,
∵∠ABE=∠BED,
∴∠EBC=∠BED,
∴BC∥DE;
∴∠ADE=∠ABC,
∵BE平分∠ABC,
∴∠ABC=2∠ABE=2×25°=50°,
∴∠ADE=50°.
23.【答案】(1)
(2)
24.【答案】(1)①,同角的余角相等;②180;
(2)①6;②或20.
一、单选题
1.如图,平分,点P射线上一点,于点M,点N射线OA上的一个动点,若,则的长度不可能是( )
A.3 B.4 C.5 D.6
2.如图,在中,的平分线交于点是中点,且,那么的度数为( )
A. B. C. D.
3.如图,直线AB、CD相交于点O,射线OM平分∠AOC,ON⊥OM.若∠BOD=70°,则∠CON的度数为( )
A.35° B.45° C.55° D.65°
4.已知和射线MN.如图,以点为圆心,任意长度为半径画弧分别交的两边于点P,Q,接着在射线MN上以点为圆心,OP长为半径画弧交射线MN于点;以为圆心,PQ长为半径画两段弧,分别交于C,D两点,连结MC,MD并延长.则的度数为( )
A. B. C. D.
5.如图,在△ABC中,∠C=90°,AC=BC,AD是∠CAB的角平分线,DE⊥AB于点E,若AB=6cm,则△DEB的周长是( )
A.5cm B.6cm C.7cm D.8cm
6.如图,在四边形中,,平分,,则的面积是( )
A.6 B.8 C.10 D.12
7.如图,△ABC中,∠ABC、∠EAC的角平分线BP、AP交于点P,延长BA、BC,PM⊥BE,PN⊥BF,则下列结论中正确的个数( )
①CP平分∠ACF;②∠ABC+2∠APC=180°;③∠ACB=2∠APB;④S△PAC=S△MAP+S△NCP.
A.1个 B.2个 C.3个 D.4个
8.如图,点E在CA延长线上,DE,AB交于点F,且∠BDE=∠AEF,∠B=∠C,∠EFA比∠FDC的余角小10°,P为线段DC上一动点,Q为PC上一点,且满足∠FQP=∠QFP,FM为∠EFP的平分线.下列结论:①CEBD;②ABCD;③FQ平分∠AFP;④∠B+∠E=140°;⑤∠QFM=20°.其中结论正确的序号是( )
A.①②③④⑤ B.①②③④ C.②③④ D.①⑤
9.如图,在中,,的外角平分线与内角平分线的延长线交于点,过点作交延长线于点,连接,点为中点.有下列结论:①;②;③;④.其中正确的是( )
A.①② B.③④ C.①②③ D.①②④
二、填空题
10.如图,直线交于点,平分,若,则 .
11.如图,的角平分线、交于点.延长至,与的延长线相交于点,且,,若的面积为6,,则线段的长度为 .
12.如图,在△ABC中,AD平分∠BAC,DE⊥AB于点E,S△ABC=15,DE=3,AB=6,则AC长是 .
13.如图:已知∠AOB=60°,OC平分∠A0B,在同一平面内以O为端点画射线OD,使∠COD=10°,则∠AOD= .
14.如图,在锐角中,,的平分线交于点D,M、分别是和上的动点,则的最小值是 .
15.如图,在△ABC中,∠C=90°,AB=10,AD是△ABC的一条角平分线.若CD=3,则△ABD的面积为
16.如图,任意画一个∠BAC=60°的△ABC,再分别作△ABC的两条角平分线BE和CD,BE和CD相交于点P,连接AP,有以下结论:①∠BPC=120°;②AP平分∠BAC;③AD=AE;④PD=PE;⑤BD+CE=BC;其中正确的结论为 .(填写序号)
17.如图,在中,和的角平分线,相交于点,于点 ,连接. 下列结论: 平分 ;;若,则 ;若 的周长为, , 则 其中正确的是 .(请填写序号)
三、解答题
18.如图,在中,,,于D,平分交于E,于F,求的度数.
19.如图所示,在中,为的角平分线,于E,于F,的面积是,,,求的长.
20.综合与探究
特例感知:(1)如图1,线段,为线段上的一个动点,点,分别是,的中点.
①若,则线段的长为___________;
②设,则线段的长为___________.
知识迁移:
(2)我们发现角的很多规律和线段一样,如图2,若,是内部的一条射线,射线平分,射线平分,求的度数.
拓展探究:
(3)已知在内的位置如图3所示,若,且,,求与的数量关系.
21.如图所示,在中,平分 ,是高线, ,,求的度数.
22.如图,已知BE平分∠ABC,点D在射线BA上,且∠ABE=∠BED,若∠ABE=25°时,求∠ADE的度数.
23.如图,直线和相交于点O,,平分.
(1)若,求的度数:
(2)若比小,求的度数.
24.已知:.
(1)如图1,若.
①写出图中一组相等的角(除直角外) ,理由是 .
②那么 .
(2)如图2,与重合,若,将绕点以5度秒的速度作逆时针旋转,运动时间为秒.
①当 秒时,平分;
②试说明:当为何值时,?
答案解析部分
1.【答案】A
2.【答案】C
3.【答案】C
4.【答案】D
5.【答案】B
6.【答案】A
7.【答案】D
8.【答案】A
9.【答案】D
10.【答案】
11.【答案】
12.【答案】4
13.【答案】20°或40°
14.【答案】
15.【答案】15
16.【答案】①②④⑤
17.【答案】
18.【答案】
19.【答案】
20.【答案】(1)①8;②;(2);(3)
21.【答案】解:∵平分 ,是高线,,
∴,,
∴,
∴,
∴的度数为.
22.【答案】解:∵BE平分∠ABC,
∴∠ABE=∠EBC,
∵∠ABE=∠BED,
∴∠EBC=∠BED,
∴BC∥DE;
∴∠ADE=∠ABC,
∵BE平分∠ABC,
∴∠ABC=2∠ABE=2×25°=50°,
∴∠ADE=50°.
23.【答案】(1)
(2)
24.【答案】(1)①,同角的余角相等;②180;
(2)①6;②或20.
