第十二章 全等三角形 章节测试卷(含简单答案)2024-2025学年人教版八年级数学上册
文档属性
| 名称 | 第十二章 全等三角形 章节测试卷(含简单答案)2024-2025学年人教版八年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 408.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-18 00:00:00 | ||
图片预览


文档简介
第十二章 全等三角形 章节测试卷2024-2025学年人教版八年级数学上册
一、单选题
1.如图,在中,,AD是的角平分线,,,则的面积为( )
A.30 B.18 C.15 D.9
2.如图所示,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,DE=4,BC=9,则BD的长为( )
A.6 B.5 C.4 D.3
3.如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB= AC,现添加以下的哪个条件仍无法判定△ABE △ACD的是( )
A.AD= AE B.∠B=∠C C.CD=BE D.∠ADC=∠AEB
4.如图,在△ABC中,∠C=90°,AD平分∠BAC,AE=AC,下列结论中错误的是( )
A.DC=DE B.∠AED=90° C.∠ADE=∠ADC D.DB=DC
5.如图,已知,垂足为,,,则可得到,理由是( )
A. B. C. D.
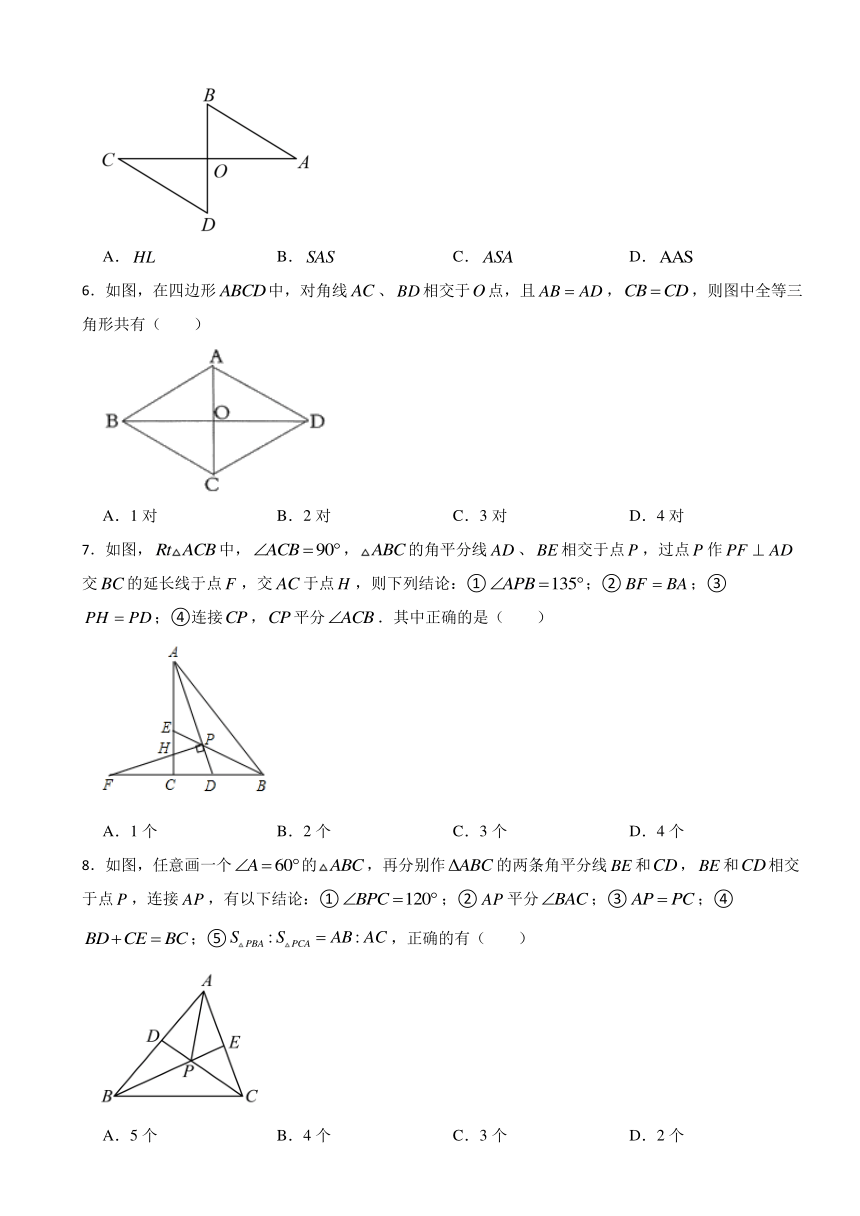
6.如图,在四边形中,对角线、相交于点,且,,则图中全等三角形共有( )
A.1对 B.2对 C.3对 D.4对
7.如图,中,,的角平分线、相交于点,过点作交的延长线于点,交于点,则下列结论:①;②;③;④连接,平分.其中正确的是( )
A.1个 B.2个 C.3个 D.4个
8.如图,任意画一个的,再分别作的两条角平分线和,和相交于点,连接,有以下结论:①;②平分;③;④;⑤,正确的有( )
A.5个 B.4个 C.3个 D.2个
9.如图:CDAB,BC平分∠ACD,CF平分∠ACG,∠BAC=40°,∠1=∠2,则下列结论:①∠ACE=2∠4;②CB⊥CF;③∠1=70°;④∠3=2∠4,其中正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
10.在△ABC中∠ACB=90°,分别过点B,C作∠BAC平分线的垂线,垂足分别为点D,E,BC的中点是M,连接CD,MD,ME.则下列结论错误的是( )
A.CD=2ME B.ME∥AB C.BD=CD D.ME=MD
二、填空题
11.已知:.求作:的平分线.
作法:(1)以点为圆心,适当长为半径画弧,交于点,交于点;(2)分别以点,为圆心,大于的长为半径画弧,两弧在的内部相交于点;(3)画射线,射线即为所求(如图).
从上述作法中可以判断,其依据是 (在“”“”“”“”中选填)
12.如图,于点B,于点D,.若添加一个条件可使用“”判定,则添加的条件为 .
13.如图,为的角平分线,,,则与的面积之比为 .
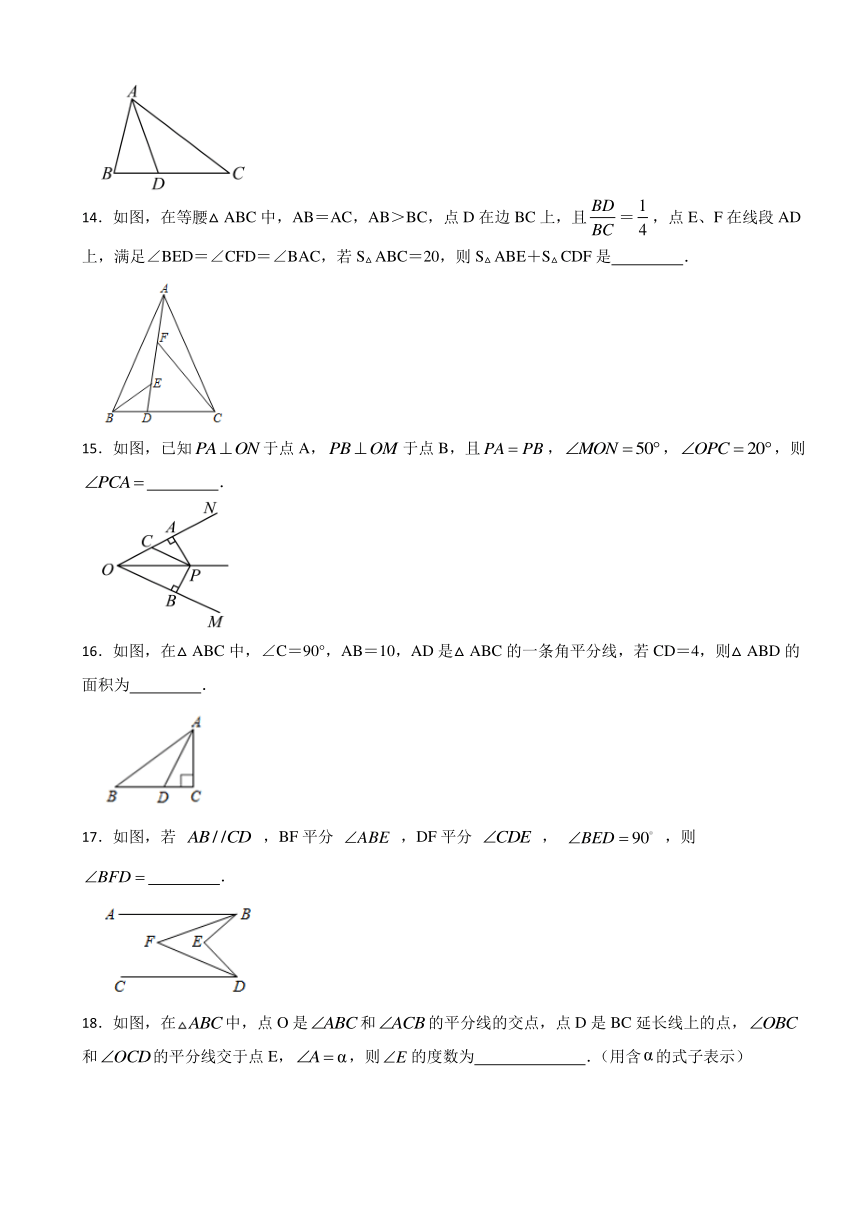
14.如图,在等腰△ABC中,AB=AC,AB>BC,点D在边BC上,且=,点E、F在线段AD上,满足∠BED=∠CFD=∠BAC,若S△ABC=20,则S△ABE+S△CDF是 .
15.如图,已知于点A,于点B,且,,,则 .
16.如图,在△ABC中,∠C=90°,AB=10,AD是△ABC的一条角平分线,若CD=4,则△ABD的面积为 .
17.如图,若 ,BF平分 ,DF平分 , ,则 .
18.如图,在中,点O是和的平分线的交点,点D是BC延长线上的点,和的平分线交于点E,,则的度数为 .(用含的式子表示)
三、解答题
19.如图,,与为对应角,与为对应边.
(1)写出其他对应边及对应角;
(2)若,,求的长.
20.如图,直线AB,CD相交于点O,OE平分∠BOC,∠FOD=90°.
(1)若∠AOF=50°,求∠BOE的度数;
(2)若∠BOD:∠BOE=1:4,求∠AOF的度数.
21.如图,,,,证明:≌.
22.如图所示,为方便游客观赏的需要,需要在人工湖两侧A,B两点之间修建一条观光步道,但无法直接量出A,B两点之间的距离,现在有一足够长的米尺,请你利用所学数学知识,设计一种方案,大致测出A,B两点之间的距离,并说明理由.
23.如图,平分,平分,且,
(1)当,________;
(2)当,________;
(3)试猜想与的数量关系,并说明理由.
24.如图,点O为直线AB上一点,∠BOC=40°,OD平分∠AOC.
(1)求∠AOD的度数;
(2)作射线OE,使∠BOE=∠COE,求∠COE的度数;
(3)在(2)的条件下,作∠FOH=90°,使射线OH在∠BOE的内部,且∠DOF=3∠BOH,直接写出∠AOH的度数.
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】C
4.【答案】D
5.【答案】A
6.【答案】C
7.【答案】D
8.【答案】B
9.【答案】C
10.【答案】A
11.【答案】
12.【答案】
13.【答案】∶
14.【答案】15
15.【答案】
16.【答案】20
17.【答案】45°
18.【答案】
19.【答案】(1)其他对应边:和,和;对应角:和,和;
(2)
20.【答案】(1)∠BOE=70°;
(2)∠AOF=70°.
21.【答案】证明:,
,即,
在与中,
≌.
22.【答案】解:在点A,B一侧的池塘边的平地上取一点P,连PA并延长到 C,使PA=PC,连BP并延长到D,使PB=PD,连接CD.
在△PAB和△PCD中,
,
∴ ,
∴AB=CD,
故量取CD的长度,即为A,B两点之间的距离.
23.【答案】(1)45°;(2)45°;(3)∠DOE=∠AOB
24.【答案】(1)70°
(2)24°或120°
(3)175°或170°或140°
一、单选题
1.如图,在中,,AD是的角平分线,,,则的面积为( )
A.30 B.18 C.15 D.9
2.如图所示,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,DE=4,BC=9,则BD的长为( )
A.6 B.5 C.4 D.3
3.如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB= AC,现添加以下的哪个条件仍无法判定△ABE △ACD的是( )
A.AD= AE B.∠B=∠C C.CD=BE D.∠ADC=∠AEB
4.如图,在△ABC中,∠C=90°,AD平分∠BAC,AE=AC,下列结论中错误的是( )
A.DC=DE B.∠AED=90° C.∠ADE=∠ADC D.DB=DC
5.如图,已知,垂足为,,,则可得到,理由是( )
A. B. C. D.
6.如图,在四边形中,对角线、相交于点,且,,则图中全等三角形共有( )
A.1对 B.2对 C.3对 D.4对
7.如图,中,,的角平分线、相交于点,过点作交的延长线于点,交于点,则下列结论:①;②;③;④连接,平分.其中正确的是( )
A.1个 B.2个 C.3个 D.4个
8.如图,任意画一个的,再分别作的两条角平分线和,和相交于点,连接,有以下结论:①;②平分;③;④;⑤,正确的有( )
A.5个 B.4个 C.3个 D.2个
9.如图:CDAB,BC平分∠ACD,CF平分∠ACG,∠BAC=40°,∠1=∠2,则下列结论:①∠ACE=2∠4;②CB⊥CF;③∠1=70°;④∠3=2∠4,其中正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
10.在△ABC中∠ACB=90°,分别过点B,C作∠BAC平分线的垂线,垂足分别为点D,E,BC的中点是M,连接CD,MD,ME.则下列结论错误的是( )
A.CD=2ME B.ME∥AB C.BD=CD D.ME=MD
二、填空题
11.已知:.求作:的平分线.
作法:(1)以点为圆心,适当长为半径画弧,交于点,交于点;(2)分别以点,为圆心,大于的长为半径画弧,两弧在的内部相交于点;(3)画射线,射线即为所求(如图).
从上述作法中可以判断,其依据是 (在“”“”“”“”中选填)
12.如图,于点B,于点D,.若添加一个条件可使用“”判定,则添加的条件为 .
13.如图,为的角平分线,,,则与的面积之比为 .
14.如图,在等腰△ABC中,AB=AC,AB>BC,点D在边BC上,且=,点E、F在线段AD上,满足∠BED=∠CFD=∠BAC,若S△ABC=20,则S△ABE+S△CDF是 .
15.如图,已知于点A,于点B,且,,,则 .
16.如图,在△ABC中,∠C=90°,AB=10,AD是△ABC的一条角平分线,若CD=4,则△ABD的面积为 .
17.如图,若 ,BF平分 ,DF平分 , ,则 .
18.如图,在中,点O是和的平分线的交点,点D是BC延长线上的点,和的平分线交于点E,,则的度数为 .(用含的式子表示)
三、解答题
19.如图,,与为对应角,与为对应边.
(1)写出其他对应边及对应角;
(2)若,,求的长.
20.如图,直线AB,CD相交于点O,OE平分∠BOC,∠FOD=90°.
(1)若∠AOF=50°,求∠BOE的度数;
(2)若∠BOD:∠BOE=1:4,求∠AOF的度数.
21.如图,,,,证明:≌.
22.如图所示,为方便游客观赏的需要,需要在人工湖两侧A,B两点之间修建一条观光步道,但无法直接量出A,B两点之间的距离,现在有一足够长的米尺,请你利用所学数学知识,设计一种方案,大致测出A,B两点之间的距离,并说明理由.
23.如图,平分,平分,且,
(1)当,________;
(2)当,________;
(3)试猜想与的数量关系,并说明理由.
24.如图,点O为直线AB上一点,∠BOC=40°,OD平分∠AOC.
(1)求∠AOD的度数;
(2)作射线OE,使∠BOE=∠COE,求∠COE的度数;
(3)在(2)的条件下,作∠FOH=90°,使射线OH在∠BOE的内部,且∠DOF=3∠BOH,直接写出∠AOH的度数.
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】C
4.【答案】D
5.【答案】A
6.【答案】C
7.【答案】D
8.【答案】B
9.【答案】C
10.【答案】A
11.【答案】
12.【答案】
13.【答案】∶
14.【答案】15
15.【答案】
16.【答案】20
17.【答案】45°
18.【答案】
19.【答案】(1)其他对应边:和,和;对应角:和,和;
(2)
20.【答案】(1)∠BOE=70°;
(2)∠AOF=70°.
21.【答案】证明:,
,即,
在与中,
≌.
22.【答案】解:在点A,B一侧的池塘边的平地上取一点P,连PA并延长到 C,使PA=PC,连BP并延长到D,使PB=PD,连接CD.
在△PAB和△PCD中,
,
∴ ,
∴AB=CD,
故量取CD的长度,即为A,B两点之间的距离.
23.【答案】(1)45°;(2)45°;(3)∠DOE=∠AOB
24.【答案】(1)70°
(2)24°或120°
(3)175°或170°或140°
