第二十二章 二次函数 章节测试卷(含简单答案)2024-2025学年人教版九年级数学上册
文档属性
| 名称 | 第二十二章 二次函数 章节测试卷(含简单答案)2024-2025学年人教版九年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 298.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-18 00:00:00 | ||
图片预览




文档简介
第二十二章 二次函数 章节测试卷2024-2025学年人教版九年级数学上册
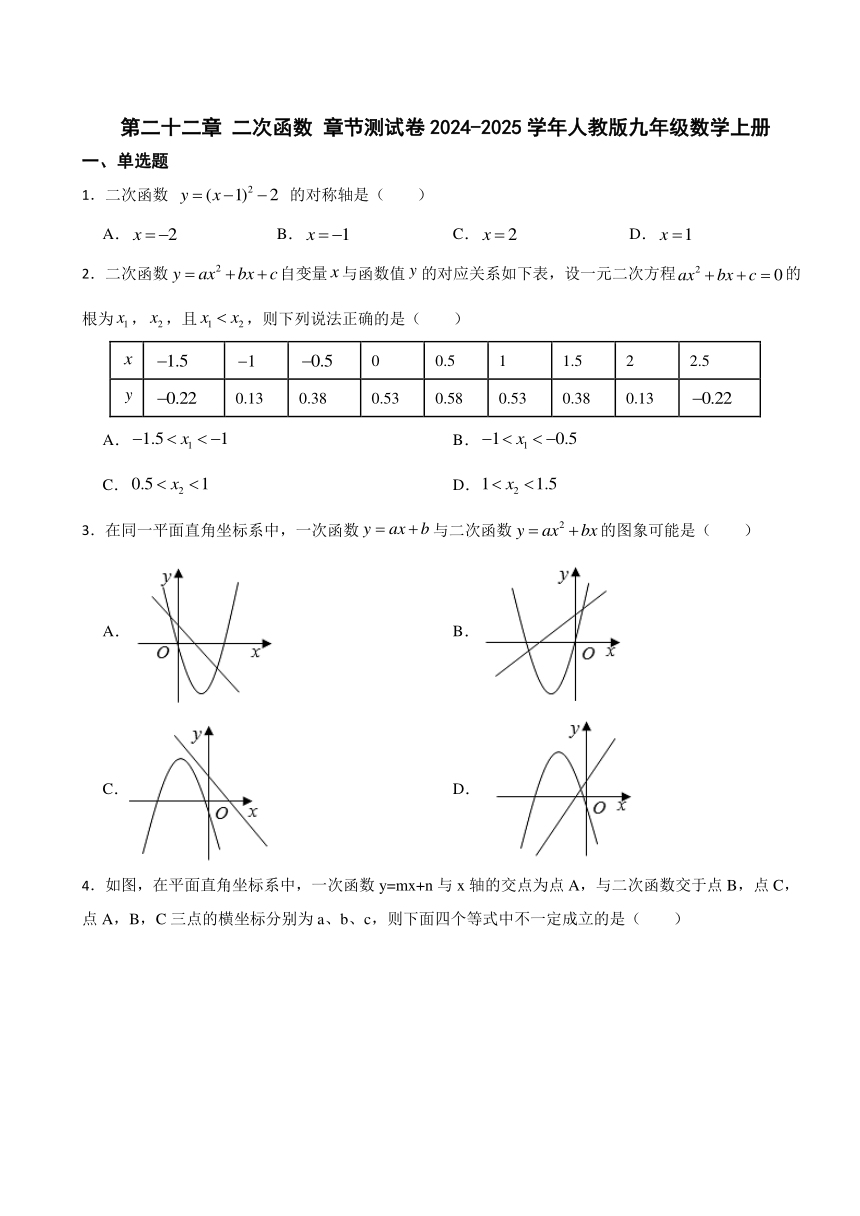
一、单选题
1.二次函数 的对称轴是( )
A. B. C. D.
2.二次函数自变量与函数值的对应关系如下表,设一元二次方程的根为,,且,则下列说法正确的是( )
0 0.5 1 1.5 2 2.5
0.13 0.38 0.53 0.58 0.53 0.38 0.13
A. B.
C. D.
3.在同一平面直角坐标系中,一次函数与二次函数的图象可能是( )
A. B.
C. D.
4.如图,在平面直角坐标系中,一次函数y=mx+n与x轴的交点为点A,与二次函数交于点B,点C,点A,B,C三点的横坐标分别为a、b、c,则下面四个等式中不一定成立的是( )
A.a2+bc=c2-ab B.
C.b2(c-a)=c2(b-a) D.
5.将抛物线 先向下平移 个单位,再向左平移 个单位,那么所得新抛物线的解析式是( )
A. B. C. D.
6.已知x2+bx-3=0的一根为x= -3,在二次函数 y= x2+2x-3 的图象上有三点 、 、 ,y1、y2、y3的大小关系是( )
A. y1<y2<y3 B.y2<y1<y3 C.y3<y1<y2 D. y1<y3<y2
7.把二次函数y=ax2+bx+c(a>0)的图象作关于x轴的对称变换,所得图象的解析式为y=﹣a(x﹣1)2+2a,若(m﹣1)a+b+c≤0,则m的最大值是( )
A.0 B.1 C.2 D.4
8.如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,则下列结论:
①2a+b+c>0;②a﹣b+c<0;③x(ax+b)≤a+b;④a<﹣1.
其中正确的有( )
A.4个 B.3个 C.2个 D.1个
9.已知二次函数的图象如图所示,下列四个命题:①;②;③若,是该抛物线上的两点,则;④若,是该抛物线上的两点,则;其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
10.设函数,,.直线x=b的图象与函数y1,y2,y3的图象分别交于点A(b,c1),B(b,c2),C(b,c3),( )
A.若b<a1<a2<a3,则c2<c3<c1 B.若a1<b<a2<a3,则c1<c2<c3
C.若a1<a2<b<a3,则c3<c2<c1 D.若a1<a2<a3<b,则c3<c2<c1
二、填空题
11.已知抛物线在轴的上方,则的取值范围是 .
12.二次函数y=x2+1的图象的顶点坐标是 .
13.如图,一个横截面为抛物线的隧道,其底部的宽为,拱高为.该隧道为双向车道,且两车之间有的隔离带,一辆宽为的货车要安全通过这条隧道,需保持其顶部隧道有不少于的空隙,则该货车能够安全通行的最大高度是 m.
14.学校卫生间的洗手盘台面上有一瓶洗手液(如图①)小丽经过测量发现:洗手液瓶子的截面图下部分是矩形CGHD,洗手液瓶子的底面直径GH=12cm,D,H与喷嘴位置点B三点共线.当小丽按住顶部A下压至如图②位置时,洗手液从喷口B流出(此时喷嘴位置点B距台面的距离为16cm),路线近似呈抛物线状,小丽在距离台面15cm处接洗手液时,手心Q到直线DH的水平距离为4cm,若小丽不去接,则洗手液落在台面的位置距DH的水平距离是16cm.根据小丽测量所得数据,可得洗手液喷出时的抛物线函数解析式的二次项系数是 。
15.已知抛物线的对称轴是,若关于x的方程的一个根是3,那么该方程的另一个根是 .
16.如图,抛物线y=ax2+bx+c与x轴相交于A、B两点,点A在点B左侧,顶点在折线M﹣P﹣N上移动,它们的坐标分别为M(﹣1,4)、P(3,4)、N(3,1).若在抛物线移动过程中,点A横坐标的最小值为﹣3,则a﹣b+c的最小值是 .
三、解答题
17.如图,已知抛物线经过两点.
(1)求抛物线的函数表达式;
(2)二次函数的最值.
18.如图,在喷水池的中心A处竖直安装一个水管AB.水管的顶端安有一个喷水管、使喷出的抛物线形水柱在与池中心A的水平距离为1m处达到最高点C.高度为3m.水柱落地点D离池中心A处3m.建立适当的平面直角坐标系,解答下列问题.
(1)求水柱所在抛物线的函数解析式;
(2)求水管AB的长.
19.已知二次函数的顶点坐标为 ,且经过点 ,设二次函数图象与y轴交于点A,求点A的坐标.
20.如图,在中,,,,点P从点A开始沿边向点B以的速度移动,点Q从点B开始沿边向点C以的速度移动.如果P,Q分别从点A,B同时出发;
(1)经过几秒的面积等于?
(2)在运动过程中,的面积有最 值(填“大”或“小”),是 .
21.把函数化为形式,并指出它的顶点坐标,对称轴,当x为何值时,y随x的增大而减小.
22.如图,已知抛物线经过、两点,其对称轴与轴交于点.
(1)求该抛物线和直线的解析式;
(2)设抛物线与直线相交于点,求的面积.
23.某商场经营某种品牌的玩具,购进的单价是30元,根据市场调查,在一段时间内,销售单价是40元时,销售量是600元,而销售单价每涨1元,就会少售出10件玩具.
(1)设该种品牌玩具的销售单价为x元,请你分别用x的代数式来表示销售量y件和销售该品牌玩具获利润W元;
(2)在(1)的条件下,若商场获利了10000元销售利润,求该玩具销售单价x应定为多少元?
(3)在(1)的条件下,若玩具厂规定该品牌玩具销售单价不低于45元,且商场要完成不少于480件的销售任务,求商场销售该品牌玩具获利的最大利润是多少元?
答案解析部分
1.【答案】D
2.【答案】A
3.【答案】B
4.【答案】A
5.【答案】B
6.【答案】A
7.【答案】D
8.【答案】A
9.【答案】B
10.【答案】D
11.【答案】
12.【答案】(0,1)
13.【答案】.
14.【答案】
15.【答案】1
16.【答案】﹣15
17.【答案】(1)
(2)最小值为
18.【答案】(1)y=﹣(x﹣1)2+3(0≤x≤3);(2)2.25m
19.【答案】解:∵二次函数的顶点坐标为
∴设其解析式为: .
∵函数经过点 ,
∴ ,
∴ ,
∴ .
令 得:
∴点A的坐标为: .
20.【答案】(1)秒或秒后,的面积等于;
(2)大;9
21.【答案】,顶点坐标为,对称轴为;当时,y随x的增大而减小.
22.【答案】(1)抛物线解析式为:;直线的解析式为
(2)8
23.【答案】(1),;(2)50元或80元;(3)商场销售该品牌玩具获利的最大利润是10560元
一、单选题
1.二次函数 的对称轴是( )
A. B. C. D.
2.二次函数自变量与函数值的对应关系如下表,设一元二次方程的根为,,且,则下列说法正确的是( )
0 0.5 1 1.5 2 2.5
0.13 0.38 0.53 0.58 0.53 0.38 0.13
A. B.
C. D.
3.在同一平面直角坐标系中,一次函数与二次函数的图象可能是( )
A. B.
C. D.
4.如图,在平面直角坐标系中,一次函数y=mx+n与x轴的交点为点A,与二次函数交于点B,点C,点A,B,C三点的横坐标分别为a、b、c,则下面四个等式中不一定成立的是( )
A.a2+bc=c2-ab B.
C.b2(c-a)=c2(b-a) D.
5.将抛物线 先向下平移 个单位,再向左平移 个单位,那么所得新抛物线的解析式是( )
A. B. C. D.
6.已知x2+bx-3=0的一根为x= -3,在二次函数 y= x2+2x-3 的图象上有三点 、 、 ,y1、y2、y3的大小关系是( )
A. y1<y2<y3 B.y2<y1<y3 C.y3<y1<y2 D. y1<y3<y2
7.把二次函数y=ax2+bx+c(a>0)的图象作关于x轴的对称变换,所得图象的解析式为y=﹣a(x﹣1)2+2a,若(m﹣1)a+b+c≤0,则m的最大值是( )
A.0 B.1 C.2 D.4
8.如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,则下列结论:
①2a+b+c>0;②a﹣b+c<0;③x(ax+b)≤a+b;④a<﹣1.
其中正确的有( )
A.4个 B.3个 C.2个 D.1个
9.已知二次函数的图象如图所示,下列四个命题:①;②;③若,是该抛物线上的两点,则;④若,是该抛物线上的两点,则;其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
10.设函数,,.直线x=b的图象与函数y1,y2,y3的图象分别交于点A(b,c1),B(b,c2),C(b,c3),( )
A.若b<a1<a2<a3,则c2<c3<c1 B.若a1<b<a2<a3,则c1<c2<c3
C.若a1<a2<b<a3,则c3<c2<c1 D.若a1<a2<a3<b,则c3<c2<c1
二、填空题
11.已知抛物线在轴的上方,则的取值范围是 .
12.二次函数y=x2+1的图象的顶点坐标是 .
13.如图,一个横截面为抛物线的隧道,其底部的宽为,拱高为.该隧道为双向车道,且两车之间有的隔离带,一辆宽为的货车要安全通过这条隧道,需保持其顶部隧道有不少于的空隙,则该货车能够安全通行的最大高度是 m.
14.学校卫生间的洗手盘台面上有一瓶洗手液(如图①)小丽经过测量发现:洗手液瓶子的截面图下部分是矩形CGHD,洗手液瓶子的底面直径GH=12cm,D,H与喷嘴位置点B三点共线.当小丽按住顶部A下压至如图②位置时,洗手液从喷口B流出(此时喷嘴位置点B距台面的距离为16cm),路线近似呈抛物线状,小丽在距离台面15cm处接洗手液时,手心Q到直线DH的水平距离为4cm,若小丽不去接,则洗手液落在台面的位置距DH的水平距离是16cm.根据小丽测量所得数据,可得洗手液喷出时的抛物线函数解析式的二次项系数是 。
15.已知抛物线的对称轴是,若关于x的方程的一个根是3,那么该方程的另一个根是 .
16.如图,抛物线y=ax2+bx+c与x轴相交于A、B两点,点A在点B左侧,顶点在折线M﹣P﹣N上移动,它们的坐标分别为M(﹣1,4)、P(3,4)、N(3,1).若在抛物线移动过程中,点A横坐标的最小值为﹣3,则a﹣b+c的最小值是 .
三、解答题
17.如图,已知抛物线经过两点.
(1)求抛物线的函数表达式;
(2)二次函数的最值.
18.如图,在喷水池的中心A处竖直安装一个水管AB.水管的顶端安有一个喷水管、使喷出的抛物线形水柱在与池中心A的水平距离为1m处达到最高点C.高度为3m.水柱落地点D离池中心A处3m.建立适当的平面直角坐标系,解答下列问题.
(1)求水柱所在抛物线的函数解析式;
(2)求水管AB的长.
19.已知二次函数的顶点坐标为 ,且经过点 ,设二次函数图象与y轴交于点A,求点A的坐标.
20.如图,在中,,,,点P从点A开始沿边向点B以的速度移动,点Q从点B开始沿边向点C以的速度移动.如果P,Q分别从点A,B同时出发;
(1)经过几秒的面积等于?
(2)在运动过程中,的面积有最 值(填“大”或“小”),是 .
21.把函数化为形式,并指出它的顶点坐标,对称轴,当x为何值时,y随x的增大而减小.
22.如图,已知抛物线经过、两点,其对称轴与轴交于点.
(1)求该抛物线和直线的解析式;
(2)设抛物线与直线相交于点,求的面积.
23.某商场经营某种品牌的玩具,购进的单价是30元,根据市场调查,在一段时间内,销售单价是40元时,销售量是600元,而销售单价每涨1元,就会少售出10件玩具.
(1)设该种品牌玩具的销售单价为x元,请你分别用x的代数式来表示销售量y件和销售该品牌玩具获利润W元;
(2)在(1)的条件下,若商场获利了10000元销售利润,求该玩具销售单价x应定为多少元?
(3)在(1)的条件下,若玩具厂规定该品牌玩具销售单价不低于45元,且商场要完成不少于480件的销售任务,求商场销售该品牌玩具获利的最大利润是多少元?
答案解析部分
1.【答案】D
2.【答案】A
3.【答案】B
4.【答案】A
5.【答案】B
6.【答案】A
7.【答案】D
8.【答案】A
9.【答案】B
10.【答案】D
11.【答案】
12.【答案】(0,1)
13.【答案】.
14.【答案】
15.【答案】1
16.【答案】﹣15
17.【答案】(1)
(2)最小值为
18.【答案】(1)y=﹣(x﹣1)2+3(0≤x≤3);(2)2.25m
19.【答案】解:∵二次函数的顶点坐标为
∴设其解析式为: .
∵函数经过点 ,
∴ ,
∴ ,
∴ .
令 得:
∴点A的坐标为: .
20.【答案】(1)秒或秒后,的面积等于;
(2)大;9
21.【答案】,顶点坐标为,对称轴为;当时,y随x的增大而减小.
22.【答案】(1)抛物线解析式为:;直线的解析式为
(2)8
23.【答案】(1),;(2)50元或80元;(3)商场销售该品牌玩具获利的最大利润是10560元
同课章节目录
