22.1.4二次函数y=a(x-h)2的图象与性质 教案
文档属性
| 名称 | 22.1.4二次函数y=a(x-h)2的图象与性质 教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 27.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-27 22:04:53 | ||
图片预览


文档简介
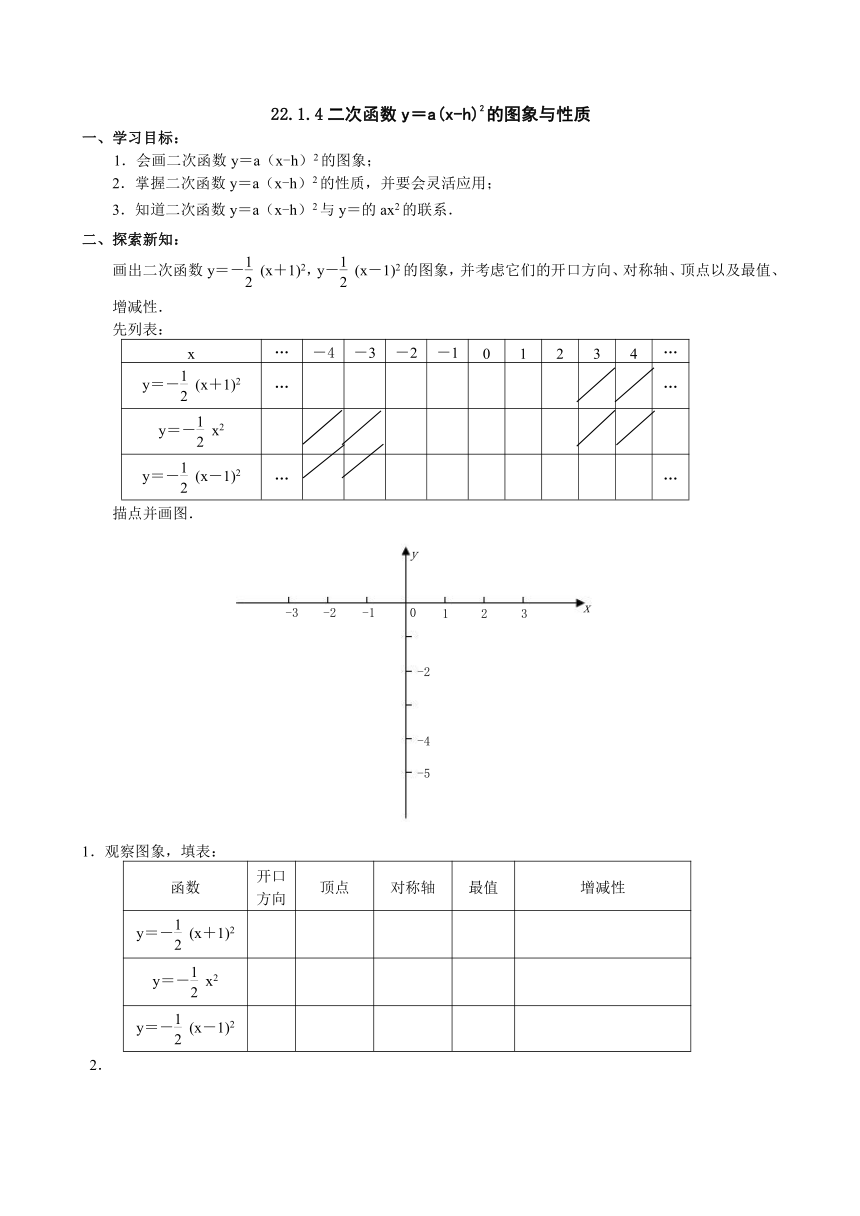
22.1.4二次函数y=a(x-h)2的图象与性质
一、学习目标:
1.会画二次函数y=a(x-h)2的图象;
2.掌握二次函数y=a(x-h)2的性质,并要会灵活应用;
3.知道二次函数y=a(x-h)2与y=的ax2的联系.
二、探索新知:
画出二次函数y=-(x+1)2,y-(x-1)2的图象,并考虑它们的开口方向、对称轴、顶点以及最值、增减性.
先列表:
x … -4 -3 -2 -1 0 1 2 3 4 …
y=-(x+1)2 … …
y=-x2
y=-(x-1)2 … …
描点并画图.
( http: / / www.21cnjy.com )
1.观察图象,填表:
函数 开口方向 顶点 对称轴 最值 增减性
y=-(x+1)2
y=-x2
y=-(x-1)2
2.
①抛物线y=-(x+1)2 ,y=-x2,y=-(x-1)2的形状大小____________.
②把抛物线y=-x2向左平移_______个单位,就得到抛物线y=-(x+1)2 ;
把抛物线y=-x2向右平移_______个单位,就得到抛物线y=-(x+1)2 .
四、整理知识点
1.
y=ax2 y=ax2+k y=a (x-h)2
开口方向 a>0时a<0时
顶点
对称轴
最值 a>0时
a<0时
2.对于二次函数的图象,只要|a|相等,则它们的形状_________,只是_________不同.
五、课堂训练
1.填表
图象(草图) 开口方向 顶点 对称轴 最值 对称轴右侧的增减性
y=x2
y=-5 (x+3)2
y=3 (x-3)2
2.抛物线y=4 (x-2)2与y轴的交点坐标是___________,与x轴的交点坐标为________.
3.把抛物线y=3x2向右平移4个单位后,得到的抛物线的表达式为______________.
把抛物线y=3x2向左平移6个单位后,得到的抛物线的表达式为_______________.
4.将抛物线y=-(x-1)2向右平移2个单位后,得到的抛物线解析式为____________.
5.写出一个顶点是(5,0),形状、开口方向与抛物线y=-2x2都相同的二次函数解析式____________.
六、目标检测
1.抛物线y=2 (x+3)2的开口__ ( http: / / www.21cnjy.com )____________;顶点坐标为__________________;对称轴是_________;当x>-3时,y______________;当x=-3时,y有_______值是_________.
2.抛物线y=m (x+n)2向左平移2个 ( http: / / www.21cnjy.com )单位后,得到的函数关系式是y=-4 (x-4)2,则 m=__________,n=___________.
3.若将抛物线y=2x2+1向下平移2个单位后,得到的抛物线解析式为______________.
4.若抛物线y=m (x+1)2过点(1,-4),则m=_______________.
5.抛物线与y轴的交点坐标是_______,与x轴的交点坐标为________.
6.已知一抛物线与抛物线y=-x2 +3形状相同,开口方向相反,顶点坐标是(-5,0)根据以上特点,该抛物线的解析式
7.将抛物线向左平移后所得新抛物线的顶点横坐标为-2,且新抛物线经过点(1,3),则的值为 .
8.将抛物线y=ax2向右 ( http: / / www.21cnjy.com )平移2个单位,再向上平移3个单位,移动后的抛物线经过点(3,-1),那么移动后的抛物线的关系式为________.
9.根据图中的抛物线,当x______时,y随x的增大而增大;当x______时,y随x的增大而减小.
10.试写出抛物线经过下列平移后得到的抛物线的解析式并写出对称轴和顶点坐标。
(1)右移2个单位;(2)左移个单位;(3)先左移1个单位,再右移4个单位。
11.二次函数的图象如图:已知,OA=OC,试求该抛物线的解析式。
( http: / / www.21cnjy.com )
一、学习目标:
1.会画二次函数y=a(x-h)2的图象;
2.掌握二次函数y=a(x-h)2的性质,并要会灵活应用;
3.知道二次函数y=a(x-h)2与y=的ax2的联系.
二、探索新知:
画出二次函数y=-(x+1)2,y-(x-1)2的图象,并考虑它们的开口方向、对称轴、顶点以及最值、增减性.
先列表:
x … -4 -3 -2 -1 0 1 2 3 4 …
y=-(x+1)2 … …
y=-x2
y=-(x-1)2 … …
描点并画图.
( http: / / www.21cnjy.com )
1.观察图象,填表:
函数 开口方向 顶点 对称轴 最值 增减性
y=-(x+1)2
y=-x2
y=-(x-1)2
2.
①抛物线y=-(x+1)2 ,y=-x2,y=-(x-1)2的形状大小____________.
②把抛物线y=-x2向左平移_______个单位,就得到抛物线y=-(x+1)2 ;
把抛物线y=-x2向右平移_______个单位,就得到抛物线y=-(x+1)2 .
四、整理知识点
1.
y=ax2 y=ax2+k y=a (x-h)2
开口方向 a>0时a<0时
顶点
对称轴
最值 a>0时
a<0时
2.对于二次函数的图象,只要|a|相等,则它们的形状_________,只是_________不同.
五、课堂训练
1.填表
图象(草图) 开口方向 顶点 对称轴 最值 对称轴右侧的增减性
y=x2
y=-5 (x+3)2
y=3 (x-3)2
2.抛物线y=4 (x-2)2与y轴的交点坐标是___________,与x轴的交点坐标为________.
3.把抛物线y=3x2向右平移4个单位后,得到的抛物线的表达式为______________.
把抛物线y=3x2向左平移6个单位后,得到的抛物线的表达式为_______________.
4.将抛物线y=-(x-1)2向右平移2个单位后,得到的抛物线解析式为____________.
5.写出一个顶点是(5,0),形状、开口方向与抛物线y=-2x2都相同的二次函数解析式____________.
六、目标检测
1.抛物线y=2 (x+3)2的开口__ ( http: / / www.21cnjy.com )____________;顶点坐标为__________________;对称轴是_________;当x>-3时,y______________;当x=-3时,y有_______值是_________.
2.抛物线y=m (x+n)2向左平移2个 ( http: / / www.21cnjy.com )单位后,得到的函数关系式是y=-4 (x-4)2,则 m=__________,n=___________.
3.若将抛物线y=2x2+1向下平移2个单位后,得到的抛物线解析式为______________.
4.若抛物线y=m (x+1)2过点(1,-4),则m=_______________.
5.抛物线与y轴的交点坐标是_______,与x轴的交点坐标为________.
6.已知一抛物线与抛物线y=-x2 +3形状相同,开口方向相反,顶点坐标是(-5,0)根据以上特点,该抛物线的解析式
7.将抛物线向左平移后所得新抛物线的顶点横坐标为-2,且新抛物线经过点(1,3),则的值为 .
8.将抛物线y=ax2向右 ( http: / / www.21cnjy.com )平移2个单位,再向上平移3个单位,移动后的抛物线经过点(3,-1),那么移动后的抛物线的关系式为________.
9.根据图中的抛物线,当x______时,y随x的增大而增大;当x______时,y随x的增大而减小.
10.试写出抛物线经过下列平移后得到的抛物线的解析式并写出对称轴和顶点坐标。
(1)右移2个单位;(2)左移个单位;(3)先左移1个单位,再右移4个单位。
11.二次函数的图象如图:已知,OA=OC,试求该抛物线的解析式。
( http: / / www.21cnjy.com )
同课章节目录
