人教版八年级数学上名师点拨精练第13章 轴对称专题证明线段相等的思路归纳(含解析)
文档属性
| 名称 | 人教版八年级数学上名师点拨精练第13章 轴对称专题证明线段相等的思路归纳(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-18 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版八年级数学上名师点拨精练
轴对称
专题 证明线段相等的思路归纳
思路一 利用全等三角形性质证明线段相等
例1.如图,点D在AB上,点E在AC上,,,求证:
针对练习1
1.如图,点C、D在线段AB上,且,,,连接CE、DE、CF、DF,求证:.
2.如图,,.
(1)求证:;
(2)若,.求的度数.
3.如图,四边中,对角线、交于点O,,点E是上一点,且,.
(1)求证:;
(2)若,,求的长.
4.如图所示,,,.求证:.
5 .如图,点E在上,,且,连接并延长,交的延长线于点F.
(1)求证:;
(2)若,,求的度数.
思路二 利用等腰三角形的性质与判定证明线段相等
例2-1 .如图,点,在的边上,,.
(1)如图1,求证:;
(2)如图2,当时,过点作于点,如果,求的值.
针对练习2
1.如图,在四边形中,,,平分交于点E.求证:.
2.如图,为中线,点E在上,交于点F,,求证:.
3.已知:如图,, 求证:.
4.如图,中,,点D在的延长线上,连接平分交于点E,过点E作,垂足为点F,与相交于点G..
(1)求证:;
(2)若,,求和的度数;
(3)求证:.
5 .如图,在中,,,D为BC的中点,过D作直线DE交直线AB与E,过D作直线,并交直线AC与F.
(1)若E点在线段AB上(非端点),则线段DE与DF的数量关系是______________;
(2)若E点在线段AB的延长线上,请你作图(用黑色水笔),此时线段DE与DF的数量关系是_____________,请说明理由.
思路三 利用线段垂直平分线的性质和判定证明线段相等
例3-1 .如图8,在△ABC中,AB=AC,∠BAC=120°,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F.
求证:BM=MN=CN.
图8
针对练习3
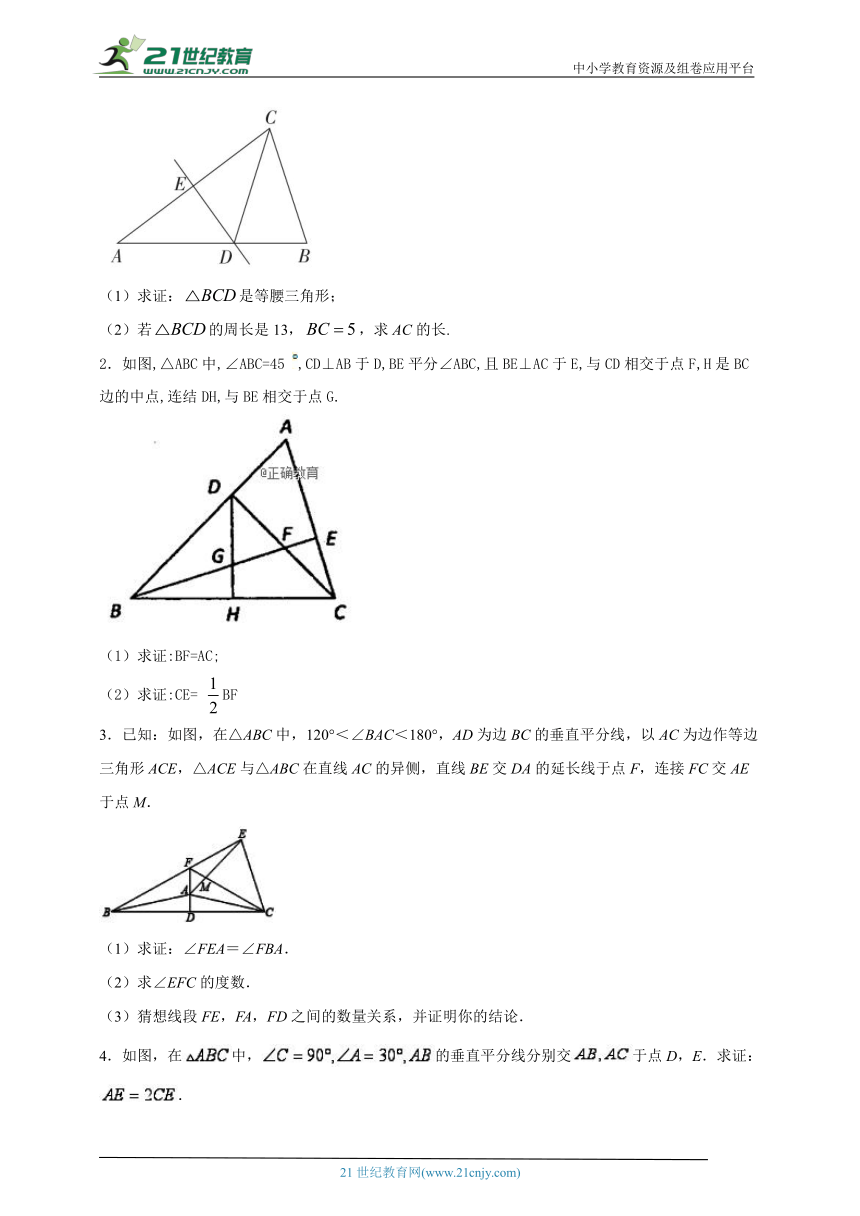
1.如图,在中,,,AC的垂直平分线DE分别交AB,AC于点D,E.
(1)求证:是等腰三角形;
(2)若的周长是13,,求AC的长.
2.如图,△ABC中,∠ABC=45 ,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH,与BE相交于点G.
(1)求证:BF=AC;
(2)求证:CE= BF
3.已知:如图,在△ABC中,120°<∠BAC<180°,AD为边BC的垂直平分线,以AC为边作等边三角形ACE,△ACE与△ABC在直线AC的异侧,直线BE交DA的延长线于点F,连接FC交AE于点M.
(1)求证:∠FEA=∠FBA.
(2)求∠EFC的度数.
(3)猜想线段FE,FA,FD之间的数量关系,并证明你的结论.
4.如图,在中,的垂直平分线分别交于点D,E.求证:.
思路四 利用角平分线的性质与判定证明线段相等
例4 .如图,△ABC中,AD是∠BAC的平分线,E、F分别为AB、AC上的点,连接DE、DF,∠EDF+∠BAC=180°.求证:DE=DF.
针对练习4
1.如图,在中,AD是它的角平分线,且,,,垂足分别为E,F.求证.
2.如图,中,AD是的平分线,,,E,F为垂足,连接EF交AD于G.
(1)求证:.
(2)试判断AD与EF的位置关系,并说明理由.
3.如图所示,的外角的平分线CF与的平分线BG相交于点O.求证:点O到三边AB,BC,AC的距离相等.
4.如图,D为BC的中点,于点D,交的平分线AE于点E, 于点F, 交AC的延长线于点G.求证:.
5.如图1,在中,,,AD,CE分别是,的平分线,AD,CE相交于点F.
(1)判断FE与FD之间的数量关系,并说明理由;
(2)如图2,如果不是直角,其他条件不变,(1)中所得结论是否仍然成立?请说明理由.
人教版八年级数学上名师点拨精练
轴对称
专题 证明线段相等的思路归纳
思路一 利用全等三角形性质证明线段相等
例1.如图,点D在AB上,点E在AC上,,,求证:
答案:证明见解析
解析:证明:在和中,
∵,
,
,
.
针对练习1
1.如图,点C、D在线段AB上,且,,,连接CE、DE、CF、DF,求证:.
答案:见解析
解析:,
,
即:,
,
,
,
,
.
2.如图,,.
(1)求证:;
(2)若,.求的度数.
答案:(1)见详解
(2)
解析:(1)证明:在与中,
,
,
;
(2),
,
,.
,
.
3.如图,四边中,对角线、交于点O,,点E是上一点,且,.
(1)求证:;
(2)若,,求的长.
答案:(1)见解析
(2)3
解析:(1),
,
即:,
在和中,
,
,
;
(2),
,
,,
.
4.如图所示,,,.求证:.
答案:见解析
解析:证明:,
,
即,
在和中,
,
,
.
5 .如图,点E在上,,且,连接并延长,交的延长线于点F.
(1)求证:;
(2)若,,求的度数.
【答案】(1)见解析
(2)
【分析】(1)由得到,证明即可;
(2)推导,即解题即可.
【详解】(1)证明:∵,
∴,
在和中,
,
∴,
∴;
(2)解:,
∴,
∵,
∴,
∵
∴,
∵,
∴,
∴.
【点睛】本题考查全等三角形的判定与性质,灵活运用全等三角形的判定方法是解题的关键.
思路二 利用等腰三角形的性质与判定证明线段相等
例2-1 .如图,点,在的边上,,.
(1)如图1,求证:;
(2)如图2,当时,过点作于点,如果,求的值.
【答案】(1)见解析
(2)4
【分析】(1)过作于点,根据三线合一可得:,,即可证明;
(2)过作于点,易证,可得,即可求解.
【详解】(1)证明:如图过作于点,
∵,,
∴,
∵,
∴,
∴;
(2)解:过作于点,
在和中,
∴,
∴,
∴.
【点睛】本题考查了全等三角形的性质与判定,等腰三角形的性质“三线合一”,熟练掌握全等三角形的判定方法是解题的关键.
针对练习2
1.如图,在四边形中,,,平分交于点E.求证:.
【答案】证明见解析.
【分析】根据平行线的性质,等角对等边证明即可.
本题考查了平行线的性质,等角对等边,熟练掌握平行线的性质,等腰三角形的判定定理是解题的关键.
【详解】证明:平分,
,
,
,
.
2.如图,为中线,点E在上,交于点F,,求证:.
【答案】见解析
【分析】本题考查了全等三角形的判定与性质.延长至点,使,连接.结合题意可证明,得到,.由,可得,结合,得到,即可求解.
【详解】解:如图,延长至点,使,连接.
为的中线,
.
在和中,
,
,
,.
,
.
,
,
,
.
3.已知:如图,, 求证:.
【答案】证明见解析
【分析】本题主要考查了全等三角形的性质与判定,等角对等边等等,证明得到,即可证明.
【详解】证明:在和中,
,
∴,
∴,
∴.
4.如图,中,,点D在的延长线上,连接平分交于点E,过点E作,垂足为点F,与相交于点G..
(1)求证:;
(2)若,,求和的度数;
(3)求证:.
【答案】(1)见解析
(2)
(3)见解析
【分析】题目主要考查角平分线的计算及三角形内角和定理,等角对等边,理解题意,找准各角之间的关系是解题关键.
(1)根据等边对等角得出,再由等角的余角相等得出,利用等角对等边即可证明;
(2)根据角平分析及等边对等角得出,再由三角形内角和定理即可求解;
(3)根据三角形内角和定理得出,,即可证明.
【详解】(1)证明:∵,
∴.
∵,
∴.
∴,
∴.
∵,
∴.
∴.
(2)解:∵平分,
∴.
∵,
∴.
在中,.
在中,.
(3)证明:在中,
.
在中,
.
∴.
5 .如图,在中,,,D为BC的中点,过D作直线DE交直线AB与E,过D作直线,并交直线AC与F.
(1)若E点在线段AB上(非端点),则线段DE与DF的数量关系是______________;
(2)若E点在线段AB的延长线上,请你作图(用黑色水笔),此时线段DE与DF的数量关系是_____________,请说明理由.
【答案】(1)
(2)图见解析,,理由见解析
【分析】(1)连接,先根据等腰直角三角形的性质可得,,再根据垂直的定义、等量代换可得,然后根据三角形全等的判定证出,根据全等三角形的性质即可得出结论;
(2)分①当点在线段的延长线上,且在的下方时,②当点在线段的延长线上,且在的上方时两种情况,参考(1)的思路,根据三角形全等的判定与性质即可得出结论.
【详解】(1)解:如图,连接,
在中,,,为的中点,
,
,
,
,
,
在和中,,
,
,
故答案为:.
(2)解:,理由如下:
①如图,当点在线段的延长线上,且在的下方时,
如图,连接,
在中,,,为的中点,
,
,
,
,
,
在和中,,
,
;
②如图,当点在线段的延长线上,且在的上方时,
如图,连接,
在中,,,为的中点,
,
,
,
,
,
在和中,,
,
;
综上,线段与的数量关系是,
故答案为:.
【点睛】本题考查了等腰直角三角形的性质、三角形全等的判定与性质等知识点,通过作辅助线,构造全等三角形是解题关键.
思路三 利用线段垂直平分线的性质和判定证明线段相等
例3-1 .如图8,在△ABC中,AB=AC,∠BAC=120°,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F.
求证:BM=MN=CN.
图8
证明:如图,连接AN,AM.
∵ME垂直平分AB,NF垂直平分AC,
∴BM=AM,CN=AN.
∴∠MAB=∠B,∠CAN=∠C.
∵∠BAC=120°,AB=AC,
∴∠B=∠C=30°.
∴∠AMN=∠ANM=60°,
则△AMN是等边三角形.
∴AM=AN=MN.
∴BM=MN=CN.
针对练习3
1.如图,在中,,,AC的垂直平分线DE分别交AB,AC于点D,E.
(1)求证:是等腰三角形;
(2)若的周长是13,,求AC的长.
答案:(1)证明见解析
(2)8
解析:(1)证明:,,
.
DE是AC的垂直平分线,
,
,
,
,
,
是等腰三角形;
(2)解:的周长是13,
,
,
,即,
,
,
.
2.如图,△ABC中,∠ABC=45 ,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH,与BE相交于点G.
(1)求证:BF=AC;
(2)求证:CE= BF
答案:(1.证明:∵DH垂直平分BC,且∠ABC=45°,∴BD=DC,且∠BDC=90°,
∵∠A+∠ABF=90°,∠A+∠ACD=90°,
∴∠ABF=∠ACD,
∴△BDF≌△CDA,
∴BF=AC.
(2.由第1题得BF=AC,∵BE平分∠ABC,且BE⊥AC,
∴在△ABE和△CBE中,
∠ABE=∠CBE BE=BE
∠AEB=∠CEB=90° ,
∴△ABE≌△CBE(ASA),
∴CE=AE=AC=BF.
3.已知:如图,在△ABC中,120°<∠BAC<180°,AD为边BC的垂直平分线,以AC为边作等边三角形ACE,△ACE与△ABC在直线AC的异侧,直线BE交DA的延长线于点F,连接FC交AE于点M.
(1)求证:∠FEA=∠FBA.
(2)求∠EFC的度数.
(3)猜想线段FE,FA,FD之间的数量关系,并证明你的结论.
【答案】(1)证明见解析
(2)60° (3)FE+FA=2FD,证明见解析
【解析】(1)由等边三角形的性质及线段的垂直平分线的性质证明;
(2)利用角之间的相等关系进行等量代换,再根据等边三角形的性质可得出答案;
(3)在CF上取 N使得FN=FE,利用(2)的结论,证明△EFN是等边三角形,得到∠FEN=∠FNE=60°,EN=EF,再证明△EFA≌△ENC(SAS),得到FA=NC,FE+FA=FN+NC=FC,再利用直角三角形中30°角所对直角边等于斜边的一半得到FC=2FD,结论得证.
【小问1详解】
解:∵AD为边BC的垂直平分线,
∴AB=AC,
∵△ACE为等边三角形,
∴AC=AE,
∴AB=AE,
∴∠FEA=∠FBA;
【小问2详解】
解:∵AD为边BC的垂直平分线
∴AB=AC,FB=FC,
∴∠ABC=∠ACB,∠FBC=∠FCB,
∴∠FBC-∠ABC=∠FCB-∠ACB,即∠ABE=∠ACF,
∵∠ABE=∠AEF,
∴∠AEF=∠ACF,
∵∠FME=∠CMA,
∴∠EFC=∠CAE,
∵等边三角形ACE中,∠CAE=60°,
∴∠EFC=60°.
【小问3详解】
解:FE+FA=2FD,
证明:CF上取 N使得FN=FE,
由(2)得∠EFM=∠CAM=60°,
∵FN=FE,
∴△EFN是等边三角形,
∴∠FEN=∠FNE=60°,EN=EF,
∵△ACE为等边三角形,
∴∠AEC=60°,EA=EC,
∴∠FEN=∠AEC,
∴∠FEN-∠MEN=∠AEC-∠MEN,即∠AEF=∠CEN,
在△EFA和∠ENC中,
EF=EN,∠AEF=∠CEN,EA=EC,
∴△EFA≌△ENC(SAS),
∴FA=NC,
∴FE+FA=FN+NC=FC,
∵∠EFC=∠FBC+∠FCB=60°,∠FBC=∠FCB,
∴∠FCB=×60°=30°,
∵AD⊥BC,
∴∠FDC=90°,
∴FC=2FD,
∴FE+FA=2FD.
【点睛】本题考查了等腰三角形的性质,等边三角形的性质和判定,含30°角的直角三角形的性质,全等三角形的性质和判定的应用及线段的垂直平分线的性质,熟练掌握相关判定和性质是解题的关键.
4.如图,在中,的垂直平分线分别交于点D,E.求证:.
【答案】证明见解析
【解析】如图,连接证明 再求解 可得 从而可得答案.
证明:如图,连接
的垂直平分线分别交于点D,E,
【点睛】本题考查的是线段的垂直平分线的性质,等腰三角形的性质,含的直角三角形的性质,掌握“直角三角形中,所对的直角边是斜边的一半”是解本题的关键.
思路四 利用角平分线的性质与判定证明线段相等
例4 .如图,△ABC中,AD是∠BAC的平分线,E、F分别为AB、AC上的点,连接DE、DF,∠EDF+∠BAC=180°.求证:DE=DF.
【分析】在AB上截取AG=AF,先证明△AGD≌△AFD,得出∠AGD=∠AFD,DG=DF;再根据角的关系求出∠4=∠3,证出DE=DG,即可得出结论DE=DF.
【解析】证明:在AB上截取AG=AF,连接DG,如图所示:
∵AD是∠BAC的平分线,
∴∠1=∠2,
在△ADG与△ADF中,
AG=AF,∠1=∠2,AD=AD,
∴△AGD≌△AFD(SAS)
∴∠AGD=∠AFD,DG=DF
又∵∠AED+∠EDF+∠DFA+∠FAE=360°,∠EDF+∠BAC=180°.
∴∠AED+∠AFD=180°,
又∠4+∠AGD=180°,
∴∠4=∠3,
∴DE=DG,
∴DE=DF.
点评:本题考查了全等三角形的判定与性质、角的平分线的定义、等腰三角形的判定与性质;证明三角形全等和等腰三角形是解决问题的关键.
针对练习4
1.如图,在中,AD是它的角平分线,且,,,垂足分别为E,F.求证.
答案:证明见解析
解析:证明:是的角平分线,,,
.
在和中,
,
.
2.如图,中,AD是的平分线,,,E,F为垂足,连接EF交AD于G.
(1)求证:.
(2)试判断AD与EF的位置关系,并说明理由.
答案:(1)见解析
(2)AD垂直平分EF,理由见解析
解析:(1)证明:中,的平分线交BC于点D,,,
,
在和中,
,
,
;
(2)AD垂直平分EF;
理由如下:
,,
点D在EF的垂直平分线上,点A在EF的垂直平分线上,
AD垂直平分EF.
3.如图所示,的外角的平分线CF与的平分线BG相交于点O.求证:点O到三边AB,BC,AC的距离相等.
答案:证明:如图,过点O作交BA的延长线于点M,过点O作于点N,过点O作于点H,
的平分线CF与的平分线BG相交于点O,
,,,
即点O到三边AB,BC,AC的距离相等.
4.如图,D为BC的中点,于点D,交的平分线AE于点E, 于点F, 交AC的延长线于点G.求证:.
答案:如图,连接BE,CE.
,D为BC的中点,
.
,且AE平分,.
在和中,
5.如图1,在中,,,AD,CE分别是,的平分线,AD,CE相交于点F.
(1)判断FE与FD之间的数量关系,并说明理由;
(2)如图2,如果不是直角,其他条件不变,(1)中所得结论是否仍然成立?请说明理由.
答案:(1).理由如下:
过点F作于点M, 于点N,则,
,,
,的平分线AD,CE交于点F,
点F在的平分线上,
又,
(2)成立.理由如下:
过点F作于点M, 于点N,
则,,
,,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版八年级数学上名师点拨精练
轴对称
专题 证明线段相等的思路归纳
思路一 利用全等三角形性质证明线段相等
例1.如图,点D在AB上,点E在AC上,,,求证:
针对练习1
1.如图,点C、D在线段AB上,且,,,连接CE、DE、CF、DF,求证:.
2.如图,,.
(1)求证:;
(2)若,.求的度数.
3.如图,四边中,对角线、交于点O,,点E是上一点,且,.
(1)求证:;
(2)若,,求的长.
4.如图所示,,,.求证:.
5 .如图,点E在上,,且,连接并延长,交的延长线于点F.
(1)求证:;
(2)若,,求的度数.
思路二 利用等腰三角形的性质与判定证明线段相等
例2-1 .如图,点,在的边上,,.
(1)如图1,求证:;
(2)如图2,当时,过点作于点,如果,求的值.
针对练习2
1.如图,在四边形中,,,平分交于点E.求证:.
2.如图,为中线,点E在上,交于点F,,求证:.
3.已知:如图,, 求证:.
4.如图,中,,点D在的延长线上,连接平分交于点E,过点E作,垂足为点F,与相交于点G..
(1)求证:;
(2)若,,求和的度数;
(3)求证:.
5 .如图,在中,,,D为BC的中点,过D作直线DE交直线AB与E,过D作直线,并交直线AC与F.
(1)若E点在线段AB上(非端点),则线段DE与DF的数量关系是______________;
(2)若E点在线段AB的延长线上,请你作图(用黑色水笔),此时线段DE与DF的数量关系是_____________,请说明理由.
思路三 利用线段垂直平分线的性质和判定证明线段相等
例3-1 .如图8,在△ABC中,AB=AC,∠BAC=120°,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F.
求证:BM=MN=CN.
图8
针对练习3
1.如图,在中,,,AC的垂直平分线DE分别交AB,AC于点D,E.
(1)求证:是等腰三角形;
(2)若的周长是13,,求AC的长.
2.如图,△ABC中,∠ABC=45 ,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH,与BE相交于点G.
(1)求证:BF=AC;
(2)求证:CE= BF
3.已知:如图,在△ABC中,120°<∠BAC<180°,AD为边BC的垂直平分线,以AC为边作等边三角形ACE,△ACE与△ABC在直线AC的异侧,直线BE交DA的延长线于点F,连接FC交AE于点M.
(1)求证:∠FEA=∠FBA.
(2)求∠EFC的度数.
(3)猜想线段FE,FA,FD之间的数量关系,并证明你的结论.
4.如图,在中,的垂直平分线分别交于点D,E.求证:.
思路四 利用角平分线的性质与判定证明线段相等
例4 .如图,△ABC中,AD是∠BAC的平分线,E、F分别为AB、AC上的点,连接DE、DF,∠EDF+∠BAC=180°.求证:DE=DF.
针对练习4
1.如图,在中,AD是它的角平分线,且,,,垂足分别为E,F.求证.
2.如图,中,AD是的平分线,,,E,F为垂足,连接EF交AD于G.
(1)求证:.
(2)试判断AD与EF的位置关系,并说明理由.
3.如图所示,的外角的平分线CF与的平分线BG相交于点O.求证:点O到三边AB,BC,AC的距离相等.
4.如图,D为BC的中点,于点D,交的平分线AE于点E, 于点F, 交AC的延长线于点G.求证:.
5.如图1,在中,,,AD,CE分别是,的平分线,AD,CE相交于点F.
(1)判断FE与FD之间的数量关系,并说明理由;
(2)如图2,如果不是直角,其他条件不变,(1)中所得结论是否仍然成立?请说明理由.
人教版八年级数学上名师点拨精练
轴对称
专题 证明线段相等的思路归纳
思路一 利用全等三角形性质证明线段相等
例1.如图,点D在AB上,点E在AC上,,,求证:
答案:证明见解析
解析:证明:在和中,
∵,
,
,
.
针对练习1
1.如图,点C、D在线段AB上,且,,,连接CE、DE、CF、DF,求证:.
答案:见解析
解析:,
,
即:,
,
,
,
,
.
2.如图,,.
(1)求证:;
(2)若,.求的度数.
答案:(1)见详解
(2)
解析:(1)证明:在与中,
,
,
;
(2),
,
,.
,
.
3.如图,四边中,对角线、交于点O,,点E是上一点,且,.
(1)求证:;
(2)若,,求的长.
答案:(1)见解析
(2)3
解析:(1),
,
即:,
在和中,
,
,
;
(2),
,
,,
.
4.如图所示,,,.求证:.
答案:见解析
解析:证明:,
,
即,
在和中,
,
,
.
5 .如图,点E在上,,且,连接并延长,交的延长线于点F.
(1)求证:;
(2)若,,求的度数.
【答案】(1)见解析
(2)
【分析】(1)由得到,证明即可;
(2)推导,即解题即可.
【详解】(1)证明:∵,
∴,
在和中,
,
∴,
∴;
(2)解:,
∴,
∵,
∴,
∵
∴,
∵,
∴,
∴.
【点睛】本题考查全等三角形的判定与性质,灵活运用全等三角形的判定方法是解题的关键.
思路二 利用等腰三角形的性质与判定证明线段相等
例2-1 .如图,点,在的边上,,.
(1)如图1,求证:;
(2)如图2,当时,过点作于点,如果,求的值.
【答案】(1)见解析
(2)4
【分析】(1)过作于点,根据三线合一可得:,,即可证明;
(2)过作于点,易证,可得,即可求解.
【详解】(1)证明:如图过作于点,
∵,,
∴,
∵,
∴,
∴;
(2)解:过作于点,
在和中,
∴,
∴,
∴.
【点睛】本题考查了全等三角形的性质与判定,等腰三角形的性质“三线合一”,熟练掌握全等三角形的判定方法是解题的关键.
针对练习2
1.如图,在四边形中,,,平分交于点E.求证:.
【答案】证明见解析.
【分析】根据平行线的性质,等角对等边证明即可.
本题考查了平行线的性质,等角对等边,熟练掌握平行线的性质,等腰三角形的判定定理是解题的关键.
【详解】证明:平分,
,
,
,
.
2.如图,为中线,点E在上,交于点F,,求证:.
【答案】见解析
【分析】本题考查了全等三角形的判定与性质.延长至点,使,连接.结合题意可证明,得到,.由,可得,结合,得到,即可求解.
【详解】解:如图,延长至点,使,连接.
为的中线,
.
在和中,
,
,
,.
,
.
,
,
,
.
3.已知:如图,, 求证:.
【答案】证明见解析
【分析】本题主要考查了全等三角形的性质与判定,等角对等边等等,证明得到,即可证明.
【详解】证明:在和中,
,
∴,
∴,
∴.
4.如图,中,,点D在的延长线上,连接平分交于点E,过点E作,垂足为点F,与相交于点G..
(1)求证:;
(2)若,,求和的度数;
(3)求证:.
【答案】(1)见解析
(2)
(3)见解析
【分析】题目主要考查角平分线的计算及三角形内角和定理,等角对等边,理解题意,找准各角之间的关系是解题关键.
(1)根据等边对等角得出,再由等角的余角相等得出,利用等角对等边即可证明;
(2)根据角平分析及等边对等角得出,再由三角形内角和定理即可求解;
(3)根据三角形内角和定理得出,,即可证明.
【详解】(1)证明:∵,
∴.
∵,
∴.
∴,
∴.
∵,
∴.
∴.
(2)解:∵平分,
∴.
∵,
∴.
在中,.
在中,.
(3)证明:在中,
.
在中,
.
∴.
5 .如图,在中,,,D为BC的中点,过D作直线DE交直线AB与E,过D作直线,并交直线AC与F.
(1)若E点在线段AB上(非端点),则线段DE与DF的数量关系是______________;
(2)若E点在线段AB的延长线上,请你作图(用黑色水笔),此时线段DE与DF的数量关系是_____________,请说明理由.
【答案】(1)
(2)图见解析,,理由见解析
【分析】(1)连接,先根据等腰直角三角形的性质可得,,再根据垂直的定义、等量代换可得,然后根据三角形全等的判定证出,根据全等三角形的性质即可得出结论;
(2)分①当点在线段的延长线上,且在的下方时,②当点在线段的延长线上,且在的上方时两种情况,参考(1)的思路,根据三角形全等的判定与性质即可得出结论.
【详解】(1)解:如图,连接,
在中,,,为的中点,
,
,
,
,
,
在和中,,
,
,
故答案为:.
(2)解:,理由如下:
①如图,当点在线段的延长线上,且在的下方时,
如图,连接,
在中,,,为的中点,
,
,
,
,
,
在和中,,
,
;
②如图,当点在线段的延长线上,且在的上方时,
如图,连接,
在中,,,为的中点,
,
,
,
,
,
在和中,,
,
;
综上,线段与的数量关系是,
故答案为:.
【点睛】本题考查了等腰直角三角形的性质、三角形全等的判定与性质等知识点,通过作辅助线,构造全等三角形是解题关键.
思路三 利用线段垂直平分线的性质和判定证明线段相等
例3-1 .如图8,在△ABC中,AB=AC,∠BAC=120°,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F.
求证:BM=MN=CN.
图8
证明:如图,连接AN,AM.
∵ME垂直平分AB,NF垂直平分AC,
∴BM=AM,CN=AN.
∴∠MAB=∠B,∠CAN=∠C.
∵∠BAC=120°,AB=AC,
∴∠B=∠C=30°.
∴∠AMN=∠ANM=60°,
则△AMN是等边三角形.
∴AM=AN=MN.
∴BM=MN=CN.
针对练习3
1.如图,在中,,,AC的垂直平分线DE分别交AB,AC于点D,E.
(1)求证:是等腰三角形;
(2)若的周长是13,,求AC的长.
答案:(1)证明见解析
(2)8
解析:(1)证明:,,
.
DE是AC的垂直平分线,
,
,
,
,
,
是等腰三角形;
(2)解:的周长是13,
,
,
,即,
,
,
.
2.如图,△ABC中,∠ABC=45 ,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH,与BE相交于点G.
(1)求证:BF=AC;
(2)求证:CE= BF
答案:(1.证明:∵DH垂直平分BC,且∠ABC=45°,∴BD=DC,且∠BDC=90°,
∵∠A+∠ABF=90°,∠A+∠ACD=90°,
∴∠ABF=∠ACD,
∴△BDF≌△CDA,
∴BF=AC.
(2.由第1题得BF=AC,∵BE平分∠ABC,且BE⊥AC,
∴在△ABE和△CBE中,
∠ABE=∠CBE BE=BE
∠AEB=∠CEB=90° ,
∴△ABE≌△CBE(ASA),
∴CE=AE=AC=BF.
3.已知:如图,在△ABC中,120°<∠BAC<180°,AD为边BC的垂直平分线,以AC为边作等边三角形ACE,△ACE与△ABC在直线AC的异侧,直线BE交DA的延长线于点F,连接FC交AE于点M.
(1)求证:∠FEA=∠FBA.
(2)求∠EFC的度数.
(3)猜想线段FE,FA,FD之间的数量关系,并证明你的结论.
【答案】(1)证明见解析
(2)60° (3)FE+FA=2FD,证明见解析
【解析】(1)由等边三角形的性质及线段的垂直平分线的性质证明;
(2)利用角之间的相等关系进行等量代换,再根据等边三角形的性质可得出答案;
(3)在CF上取 N使得FN=FE,利用(2)的结论,证明△EFN是等边三角形,得到∠FEN=∠FNE=60°,EN=EF,再证明△EFA≌△ENC(SAS),得到FA=NC,FE+FA=FN+NC=FC,再利用直角三角形中30°角所对直角边等于斜边的一半得到FC=2FD,结论得证.
【小问1详解】
解:∵AD为边BC的垂直平分线,
∴AB=AC,
∵△ACE为等边三角形,
∴AC=AE,
∴AB=AE,
∴∠FEA=∠FBA;
【小问2详解】
解:∵AD为边BC的垂直平分线
∴AB=AC,FB=FC,
∴∠ABC=∠ACB,∠FBC=∠FCB,
∴∠FBC-∠ABC=∠FCB-∠ACB,即∠ABE=∠ACF,
∵∠ABE=∠AEF,
∴∠AEF=∠ACF,
∵∠FME=∠CMA,
∴∠EFC=∠CAE,
∵等边三角形ACE中,∠CAE=60°,
∴∠EFC=60°.
【小问3详解】
解:FE+FA=2FD,
证明:CF上取 N使得FN=FE,
由(2)得∠EFM=∠CAM=60°,
∵FN=FE,
∴△EFN是等边三角形,
∴∠FEN=∠FNE=60°,EN=EF,
∵△ACE为等边三角形,
∴∠AEC=60°,EA=EC,
∴∠FEN=∠AEC,
∴∠FEN-∠MEN=∠AEC-∠MEN,即∠AEF=∠CEN,
在△EFA和∠ENC中,
EF=EN,∠AEF=∠CEN,EA=EC,
∴△EFA≌△ENC(SAS),
∴FA=NC,
∴FE+FA=FN+NC=FC,
∵∠EFC=∠FBC+∠FCB=60°,∠FBC=∠FCB,
∴∠FCB=×60°=30°,
∵AD⊥BC,
∴∠FDC=90°,
∴FC=2FD,
∴FE+FA=2FD.
【点睛】本题考查了等腰三角形的性质,等边三角形的性质和判定,含30°角的直角三角形的性质,全等三角形的性质和判定的应用及线段的垂直平分线的性质,熟练掌握相关判定和性质是解题的关键.
4.如图,在中,的垂直平分线分别交于点D,E.求证:.
【答案】证明见解析
【解析】如图,连接证明 再求解 可得 从而可得答案.
证明:如图,连接
的垂直平分线分别交于点D,E,
【点睛】本题考查的是线段的垂直平分线的性质,等腰三角形的性质,含的直角三角形的性质,掌握“直角三角形中,所对的直角边是斜边的一半”是解本题的关键.
思路四 利用角平分线的性质与判定证明线段相等
例4 .如图,△ABC中,AD是∠BAC的平分线,E、F分别为AB、AC上的点,连接DE、DF,∠EDF+∠BAC=180°.求证:DE=DF.
【分析】在AB上截取AG=AF,先证明△AGD≌△AFD,得出∠AGD=∠AFD,DG=DF;再根据角的关系求出∠4=∠3,证出DE=DG,即可得出结论DE=DF.
【解析】证明:在AB上截取AG=AF,连接DG,如图所示:
∵AD是∠BAC的平分线,
∴∠1=∠2,
在△ADG与△ADF中,
AG=AF,∠1=∠2,AD=AD,
∴△AGD≌△AFD(SAS)
∴∠AGD=∠AFD,DG=DF
又∵∠AED+∠EDF+∠DFA+∠FAE=360°,∠EDF+∠BAC=180°.
∴∠AED+∠AFD=180°,
又∠4+∠AGD=180°,
∴∠4=∠3,
∴DE=DG,
∴DE=DF.
点评:本题考查了全等三角形的判定与性质、角的平分线的定义、等腰三角形的判定与性质;证明三角形全等和等腰三角形是解决问题的关键.
针对练习4
1.如图,在中,AD是它的角平分线,且,,,垂足分别为E,F.求证.
答案:证明见解析
解析:证明:是的角平分线,,,
.
在和中,
,
.
2.如图,中,AD是的平分线,,,E,F为垂足,连接EF交AD于G.
(1)求证:.
(2)试判断AD与EF的位置关系,并说明理由.
答案:(1)见解析
(2)AD垂直平分EF,理由见解析
解析:(1)证明:中,的平分线交BC于点D,,,
,
在和中,
,
,
;
(2)AD垂直平分EF;
理由如下:
,,
点D在EF的垂直平分线上,点A在EF的垂直平分线上,
AD垂直平分EF.
3.如图所示,的外角的平分线CF与的平分线BG相交于点O.求证:点O到三边AB,BC,AC的距离相等.
答案:证明:如图,过点O作交BA的延长线于点M,过点O作于点N,过点O作于点H,
的平分线CF与的平分线BG相交于点O,
,,,
即点O到三边AB,BC,AC的距离相等.
4.如图,D为BC的中点,于点D,交的平分线AE于点E, 于点F, 交AC的延长线于点G.求证:.
答案:如图,连接BE,CE.
,D为BC的中点,
.
,且AE平分,.
在和中,
5.如图1,在中,,,AD,CE分别是,的平分线,AD,CE相交于点F.
(1)判断FE与FD之间的数量关系,并说明理由;
(2)如图2,如果不是直角,其他条件不变,(1)中所得结论是否仍然成立?请说明理由.
答案:(1).理由如下:
过点F作于点M, 于点N,则,
,,
,的平分线AD,CE交于点F,
点F在的平分线上,
又,
(2)成立.理由如下:
过点F作于点M, 于点N,
则,,
,,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
