22.1.3 二次函数y=a(x-h)2+k的图象和性质(配套练习)
文档属性
| 名称 | 22.1.3 二次函数y=a(x-h)2+k的图象和性质(配套练习) |
|
|
| 格式 | zip | ||
| 文件大小 | 54.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-28 00:00:00 | ||
图片预览

文档简介
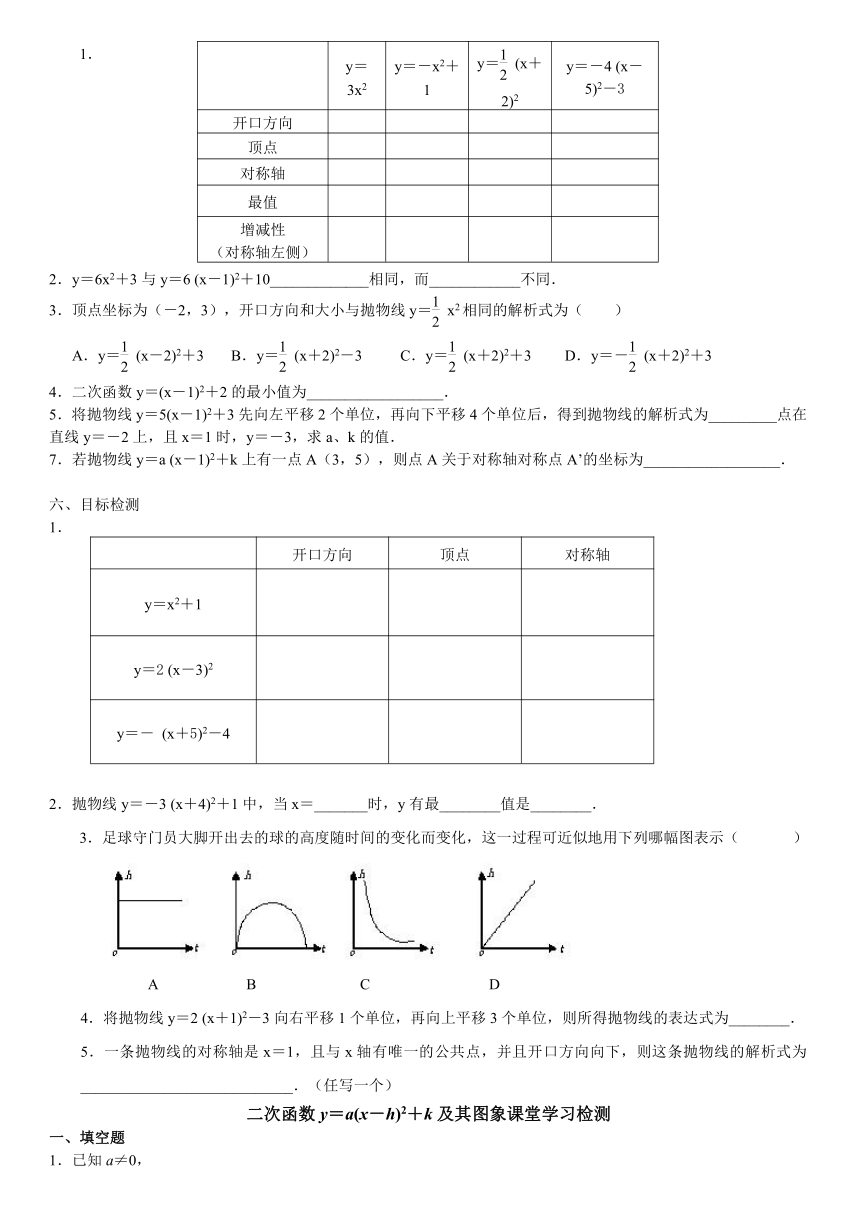
二次函数y=a(x-h)2+k的图象与性质
探索新知:
画出函数y=-(x+1)2-1的图象,指出它的开口方向、对称轴及顶点、最值、增减性.
列表:
x … -4 -3 -2 -1 0 1 2 …
y=-(x+1)2-1 … …
( http: / / www.21cnjy.com )
图象归纳:
函数 开口方向 顶点 对称轴 最值 增减性
y=-(x+1)2-1
1.
2.把抛物线y=-x2向_____平移____个单位,再向____平移_____个单位,就得到抛物线y=-(x+1)2-1.
理一理知识点
y=ax2 y=ax2+k y=a (x-h)2 y=a (x-h)2+k
开口方向
顶点
对称轴
最值
增减性(对称轴右侧)
2.抛物线y=a (x-h)2+k与y=ax2形状___________,位置________________.
课堂练习
y=3x2 y=-x2+1 y=(x+2)2 y=-4 (x-5)2-3
开口方向
顶点
对称轴
最值
增减性(对称轴左侧)
1.
2.y=6x2+3与y=6 (x-1)2+10_____________相同,而____________不同.
3.顶点坐标为(-2,3),开口方向和大小与抛物线y=x2相同的解析式为( )
A.y=(x-2)2+3 B.y=(x+2)2-3 C.y=(x+2)2+3 D.y=-(x+2)2+3
4.二次函数y=(x-1)2+2的最小值为__________________.
5.将抛物线y=5(x-1)2+3先向左 ( http: / / www.21cnjy.com )平移2个单位,再向下平移4个单位后,得到抛物线的解析式为_________点在直线y=-2上,且x=1时,y=-3,求a、k的值.
7.若抛物线y=a (x-1)2+k上有一点A(3,5),则点A关于对称轴对称点A’的坐标为__________________.
六、目标检测
1.
开口方向 顶点 对称轴
y=x2+1
y=2 (x-3)2
y=- (x+5)2-4
2.抛物线y=-3 (x+4)2+1中,当x=_______时,y有最________值是________.
3.足球守门员大脚开出去的球的高度随时间的变化而变化,这一过程可近似地用下列哪幅图表示( )
( http: / / www.21cnjy.com )
A B C D
4.将抛物线y=2 (x+1)2-3向右平移1个单位,再向上平移3个单位,则所得抛物线的表达式为________.
5.一条抛物线的对称轴是x=1,且与x轴有 ( http: / / www.21cnjy.com )唯一的公共点,并且开口方向向下,则这条抛物线的解析式为____________________________.(任写一个)
二次函数y=a(x-h)2+k及其图象课堂学习检测
一、填空题
1.已知a≠0,
(1)抛物线y=ax2的顶点坐标为______,对称轴为______.
(2)抛物线y=ax2+c的顶点坐标为______,对称轴为______.
(3)抛物线y=a(x-m)2的顶点坐标为______,对称轴为______.
2.若函数是二次函数,则m=______.
3.抛物线y=2x2的顶点,坐标为____ ( http: / / www.21cnjy.com )__,对称轴是______.当x______时,y随x增大而减小;当x______时,y随x增大而增大;当x=______时,y有最______值是______.
4.抛物线y=-2x2的开口方向是______,它的形状与y=2x2的形状______,它的顶点坐标是______,对称轴是______.
5.抛物线y=2x2+3的 ( http: / / www.21cnjy.com )顶点坐标为______,对称轴为______.当x______时,y随x的增大而减小;当x=______时,y有最______值是______,它可以由抛物线y=2x2向______平移______个单位得到.
6.抛物线y=3(x-2)2的开口方向 ( http: / / www.21cnjy.com )是______,顶点坐标为______,对称轴是______.当x______时,y随x的增大而增大;当x=______时,y有最______值是______,它可以由抛物线y=3x2向______平移______个单位得到.
二、选择题
7.要得到抛物线,可将抛物线( )
A.向上平移4个单位 B.向下平移4个单位 C.向右平移4个单位 D.向左平移4个单位
8.下列各组抛物线中能够互相平移而彼此得到对方的是( )
A.y=2x2与y=3x2 B.与 C.y=2x2与y=x2+2 D.y=x2与y=x2-2
9.顶点为(-5,0),且开口方向、形状与函数的图象相同的抛物线是( )
A. B. C. D.
三、解答题
10.在同一坐标系中画出函数和的图象,并说明y1,y2的图象与函数的图象的关系.
( http: / / www.21cnjy.com )
11.在同一坐标系中,画出函数y1 ( http: / / www.21cnjy.com )=2x2,y2=2(x-2)2与y3=2(x+2)2的图象,并说明y2,y3的图象与y1=2x2的图象的关系.
( http: / / www.21cnjy.com )
综合、运用、诊断
一、填空题
12.二次函数y=a(x-h)2+ ( http: / / www.21cnjy.com )k(a≠0)的顶点坐标是______,对称轴是______,当x=______时,y有最值______;当a>0时,若x______时,y随x增大而减小.
13.填表.
解析式 开口方向 顶点坐标 对称轴
y=(x-2)2-3
y=-(x+3)2+2
y=3(x-2)2
y=-3x2+2
14.抛物线有最______点,其坐标是______.当x=______时,y的最______值是______;当x______时,y随x增大而增大.
15.将抛物线向右平移3个单位,再向上平移2个单位,所得的抛物线的解析式为______.
二、选择题
16.一抛物线和抛物线y=-2x2的形状、开口方向完全相同,顶点坐标是(-1,3),则该抛物线的解析式为( )
A.y=-2(x-1)2+3 B.y=-2(x+1)2+3 C.y=-(2x+1)2+3 D.y=-(2x-1)2+3
17.要得到y=-2(x+2)2-3的图象,需将抛物线y=-2x2作如下平移( )
A.向右平移2个单位,再向上平移3个单位 B.向右平移2个单位,再向下平移3个单位
C.向左平移2个单位,再向上平移3个单位 D.向左平移2个单位,再向下平移3个单位
三、解答题
18.将下列函数配成y=a(x-h)2+k的形式,并求顶点坐标、对称轴及最值.
(1)y=x2+6x+10 (2)y=-2x2-5x+7
(3)y=3x2+2x (4)y=-3x2+6x-2
(5)y=100-5x2 (6)y=(x-2)(2x+1)
拓展、探究、思考
19.把二次函数y=a(x-h)2+k的图象先向左平移2个单位,再向上平移4个单位,得到二次函数的图象.
(1)试确定a,h,k的值;
(2)指出二次函数y=a(x-h)2+k的开口方向、对称轴和顶点坐标.
探索新知:
画出函数y=-(x+1)2-1的图象,指出它的开口方向、对称轴及顶点、最值、增减性.
列表:
x … -4 -3 -2 -1 0 1 2 …
y=-(x+1)2-1 … …
( http: / / www.21cnjy.com )
图象归纳:
函数 开口方向 顶点 对称轴 最值 增减性
y=-(x+1)2-1
1.
2.把抛物线y=-x2向_____平移____个单位,再向____平移_____个单位,就得到抛物线y=-(x+1)2-1.
理一理知识点
y=ax2 y=ax2+k y=a (x-h)2 y=a (x-h)2+k
开口方向
顶点
对称轴
最值
增减性(对称轴右侧)
2.抛物线y=a (x-h)2+k与y=ax2形状___________,位置________________.
课堂练习
y=3x2 y=-x2+1 y=(x+2)2 y=-4 (x-5)2-3
开口方向
顶点
对称轴
最值
增减性(对称轴左侧)
1.
2.y=6x2+3与y=6 (x-1)2+10_____________相同,而____________不同.
3.顶点坐标为(-2,3),开口方向和大小与抛物线y=x2相同的解析式为( )
A.y=(x-2)2+3 B.y=(x+2)2-3 C.y=(x+2)2+3 D.y=-(x+2)2+3
4.二次函数y=(x-1)2+2的最小值为__________________.
5.将抛物线y=5(x-1)2+3先向左 ( http: / / www.21cnjy.com )平移2个单位,再向下平移4个单位后,得到抛物线的解析式为_________点在直线y=-2上,且x=1时,y=-3,求a、k的值.
7.若抛物线y=a (x-1)2+k上有一点A(3,5),则点A关于对称轴对称点A’的坐标为__________________.
六、目标检测
1.
开口方向 顶点 对称轴
y=x2+1
y=2 (x-3)2
y=- (x+5)2-4
2.抛物线y=-3 (x+4)2+1中,当x=_______时,y有最________值是________.
3.足球守门员大脚开出去的球的高度随时间的变化而变化,这一过程可近似地用下列哪幅图表示( )
( http: / / www.21cnjy.com )
A B C D
4.将抛物线y=2 (x+1)2-3向右平移1个单位,再向上平移3个单位,则所得抛物线的表达式为________.
5.一条抛物线的对称轴是x=1,且与x轴有 ( http: / / www.21cnjy.com )唯一的公共点,并且开口方向向下,则这条抛物线的解析式为____________________________.(任写一个)
二次函数y=a(x-h)2+k及其图象课堂学习检测
一、填空题
1.已知a≠0,
(1)抛物线y=ax2的顶点坐标为______,对称轴为______.
(2)抛物线y=ax2+c的顶点坐标为______,对称轴为______.
(3)抛物线y=a(x-m)2的顶点坐标为______,对称轴为______.
2.若函数是二次函数,则m=______.
3.抛物线y=2x2的顶点,坐标为____ ( http: / / www.21cnjy.com )__,对称轴是______.当x______时,y随x增大而减小;当x______时,y随x增大而增大;当x=______时,y有最______值是______.
4.抛物线y=-2x2的开口方向是______,它的形状与y=2x2的形状______,它的顶点坐标是______,对称轴是______.
5.抛物线y=2x2+3的 ( http: / / www.21cnjy.com )顶点坐标为______,对称轴为______.当x______时,y随x的增大而减小;当x=______时,y有最______值是______,它可以由抛物线y=2x2向______平移______个单位得到.
6.抛物线y=3(x-2)2的开口方向 ( http: / / www.21cnjy.com )是______,顶点坐标为______,对称轴是______.当x______时,y随x的增大而增大;当x=______时,y有最______值是______,它可以由抛物线y=3x2向______平移______个单位得到.
二、选择题
7.要得到抛物线,可将抛物线( )
A.向上平移4个单位 B.向下平移4个单位 C.向右平移4个单位 D.向左平移4个单位
8.下列各组抛物线中能够互相平移而彼此得到对方的是( )
A.y=2x2与y=3x2 B.与 C.y=2x2与y=x2+2 D.y=x2与y=x2-2
9.顶点为(-5,0),且开口方向、形状与函数的图象相同的抛物线是( )
A. B. C. D.
三、解答题
10.在同一坐标系中画出函数和的图象,并说明y1,y2的图象与函数的图象的关系.
( http: / / www.21cnjy.com )
11.在同一坐标系中,画出函数y1 ( http: / / www.21cnjy.com )=2x2,y2=2(x-2)2与y3=2(x+2)2的图象,并说明y2,y3的图象与y1=2x2的图象的关系.
( http: / / www.21cnjy.com )
综合、运用、诊断
一、填空题
12.二次函数y=a(x-h)2+ ( http: / / www.21cnjy.com )k(a≠0)的顶点坐标是______,对称轴是______,当x=______时,y有最值______;当a>0时,若x______时,y随x增大而减小.
13.填表.
解析式 开口方向 顶点坐标 对称轴
y=(x-2)2-3
y=-(x+3)2+2
y=3(x-2)2
y=-3x2+2
14.抛物线有最______点,其坐标是______.当x=______时,y的最______值是______;当x______时,y随x增大而增大.
15.将抛物线向右平移3个单位,再向上平移2个单位,所得的抛物线的解析式为______.
二、选择题
16.一抛物线和抛物线y=-2x2的形状、开口方向完全相同,顶点坐标是(-1,3),则该抛物线的解析式为( )
A.y=-2(x-1)2+3 B.y=-2(x+1)2+3 C.y=-(2x+1)2+3 D.y=-(2x-1)2+3
17.要得到y=-2(x+2)2-3的图象,需将抛物线y=-2x2作如下平移( )
A.向右平移2个单位,再向上平移3个单位 B.向右平移2个单位,再向下平移3个单位
C.向左平移2个单位,再向上平移3个单位 D.向左平移2个单位,再向下平移3个单位
三、解答题
18.将下列函数配成y=a(x-h)2+k的形式,并求顶点坐标、对称轴及最值.
(1)y=x2+6x+10 (2)y=-2x2-5x+7
(3)y=3x2+2x (4)y=-3x2+6x-2
(5)y=100-5x2 (6)y=(x-2)(2x+1)
拓展、探究、思考
19.把二次函数y=a(x-h)2+k的图象先向左平移2个单位,再向上平移4个单位,得到二次函数的图象.
(1)试确定a,h,k的值;
(2)指出二次函数y=a(x-h)2+k的开口方向、对称轴和顶点坐标.
同课章节目录
