人教版八年级数学上名师点拨精练第13章 轴对称专题等腰三角形中的常见证明思路(含解析)
文档属性
| 名称 | 人教版八年级数学上名师点拨精练第13章 轴对称专题等腰三角形中的常见证明思路(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-18 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版八年级数学上名师点拨精练
轴对称
专题 等腰三角形中的常见证明思路
类型一、利用等腰三角形的性质证明角相等
例1. 如图,在△ABC中,是的中点,,,垂足分别是、,且.
(1)求证:.
(2)连接AD,求证:AD⊥BC.
针对练习1
1.如图,在△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
(1)求证:△ABE≌△DCE;
(2)求证:∠EBC=∠ECB.
2. 在△ABC中,AB<AC,AD为△ABC的角平分线,点E是BC边的中点.过点E作AD延长线的垂线,垂足为点G,交AC于点F,交AB的延长线于点H.
(1)求证:∠AHF=∠AFH;
(2)探究:在线段EH上是否能找到一点P,使得△BEP≌△CEF.如果能够,请找出并证明之;
(3)证明:BH=CF.
3.如图,BC⊥CA,BC=CA,DC⊥CE,DC=CE,直线BD与AE交于点F,交AC于点G,连接CF.
(1)求证:△ACE≌△BCD;
(2)求证:BF⊥AE;
(3)请判断∠CFE与∠CAB的大小关系并说明理由.
类型二、利用“三线合一”证明两线垂直
例2.如图,在中,,,试说明的理由.
解:已知,
▲
已知,
等式性质,
在与中,
,
≌ ,
,
又,
针对练习2
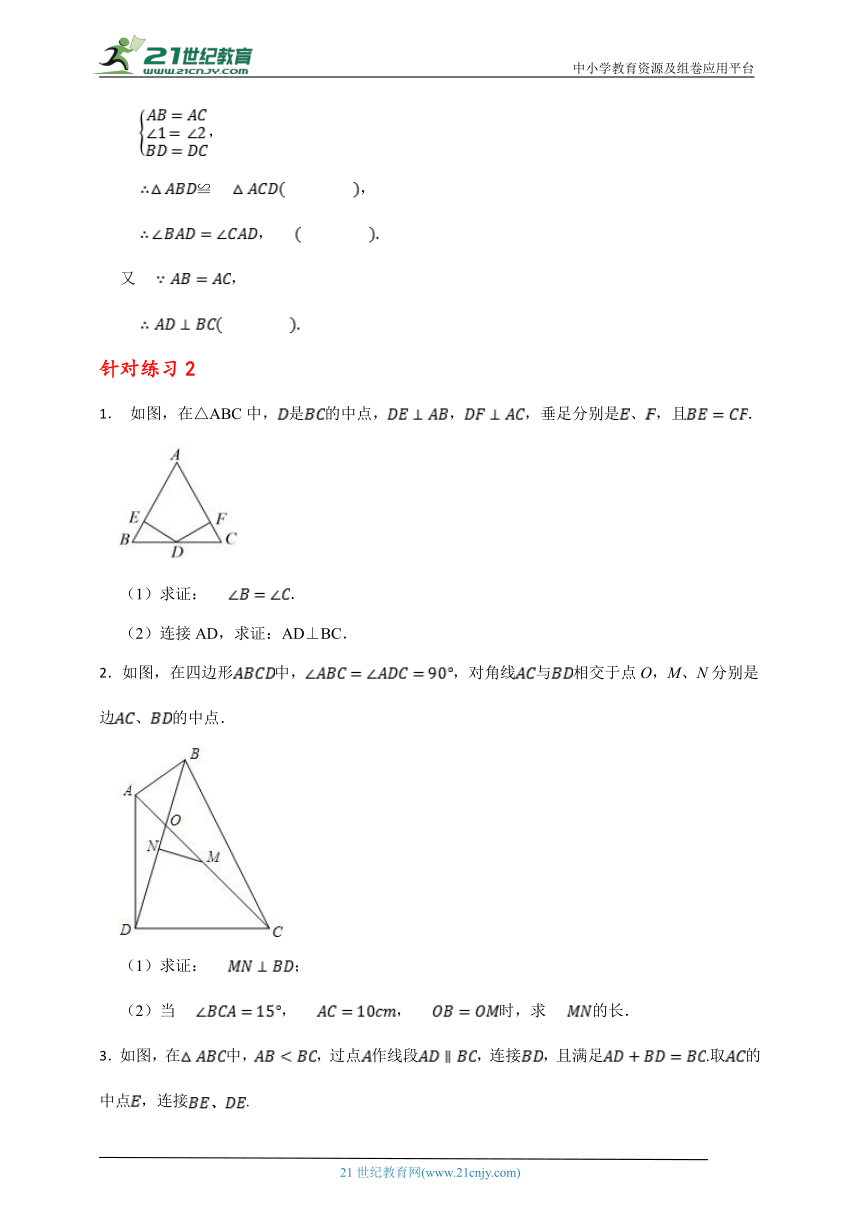
1. 如图,在△ABC中,是的中点,,,垂足分别是、,且.
(1)求证:.
(2)连接AD,求证:AD⊥BC.
2.如图,在四边形中,,对角线与相交于点O,M、N分别是边、的中点.
(1)求证:;
(2)当,,时,求的长.
3.如图,在中,,过点作线段,连接,且满足.取的中点,连接.
(1)若,直接写出的取值范围 ;
(2)求证:.
类型三、利用平行线证明等腰三角形
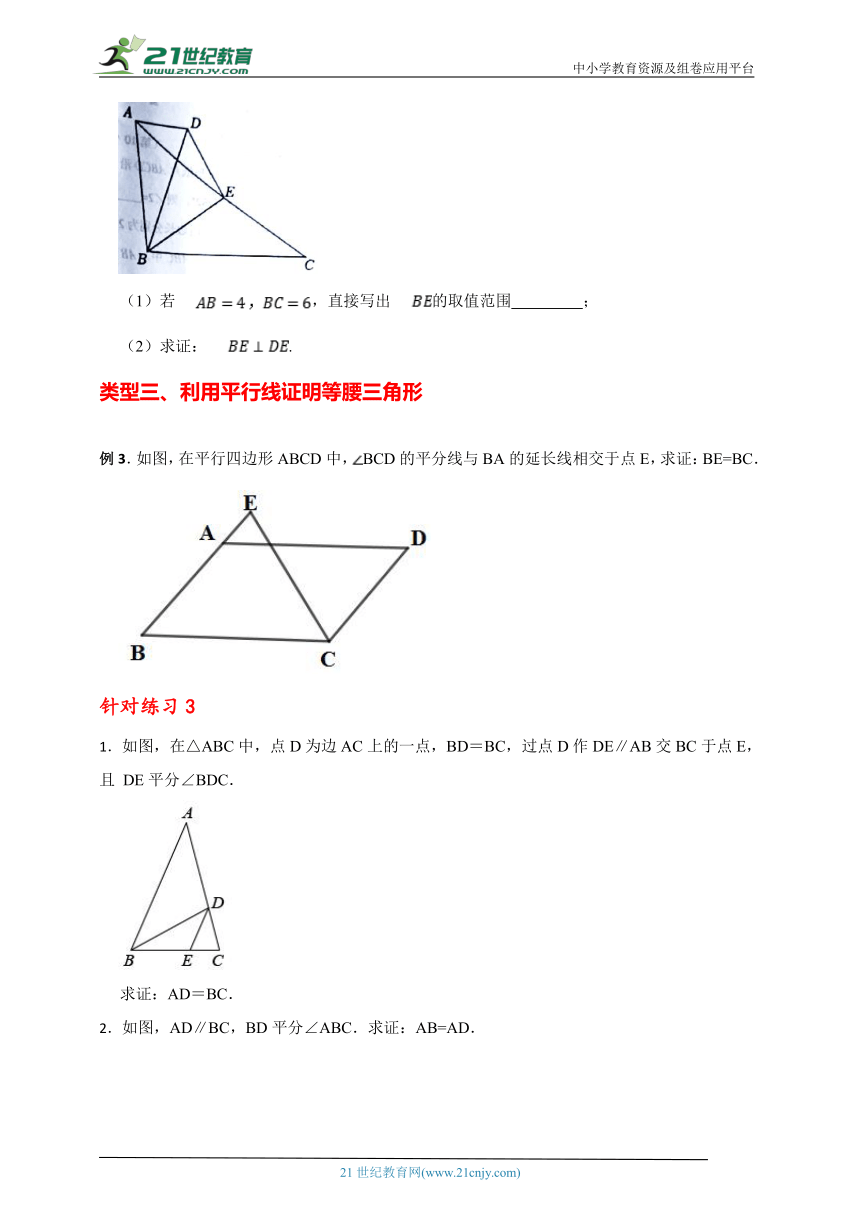
例3.如图,在平行四边形ABCD中,BCD的平分线与BA的延长线相交于点E,求证:BE=BC.
针对练习3
1.如图,在△ABC中,点D为边AC上的一点,BD=BC,过点D作DE∥AB交BC于点E,且 DE平分∠BDC.
求证:AD=BC.
2.如图,AD∥BC,BD平分∠ABC.求证:AB=AD.
3.如图所示,在四边形ABCD中,的平分线与的平分线相交于点F,与的延长线交于点E,连接.
求证:
(1)是等腰三角形.
(2)若.则________.
5.
(1)如图,中,,,的平分线交于点,过点作交,于点,图中有 个等腰三角形猜想:与,之间有怎样的关系,并说明理由;
(2)如图,若,其他条件不变,图中有 个等腰三角形;与,间的关系是 ;
(3)如图,,若的角平分线与外角的角平分线交于点,过点作交于,交于图中有 个等腰三角形与,间的数量关系是 .
类型四、利用全等三角形证明等腰三角形
例4.如图所示,AE=AD,∠B=∠C,BE=4,AD=5,则AC=_____.
针对练习4
1.已知:如图,在等腰梯形ABCD中,AD∥BC,∠BDC=∠BCD,点E是线段BD上一点,且BE=AD.
(1)证明:△ADB≌△EBC;
(2)直接写出图中所有的等腰三角形.
2.从①∠B=∠C;②∠BAD=∠CDA;③AB=DC;④BE=CE四个等式中选出两个作为条件,证明△AED是等腰三角形(写出一种即可).已知:_____(只填序号)
求证:△AED是等腰三角形.
证明:
_____.
3.如图,在△ABC中,已知点D在线段AB的反向延长线上,过AC的中点F作线段GE交∠DAC的平分线于E,交BC于G,且AE∥BC.
(1)求证:△ABC是等腰三角形.
(2)若AE=8,AB=10,GC=2BG,求△ABC的周长.
4.已知:如图,AB=DC,BD=CA,求证:△AED是等腰三角形.
类型五、等腰三角形中的探究问题
例5.如图,.
(1)写出与的数量关系
(2)延长到,使,延长到,使,连接.求证:.
(3)在(2)的条件下,作的平分线,交于点,求证:.
针对练习5
1.如图,在△ABC中,点D、E分别在BC、AC上,连接AD、DE,∠ADB+∠EDC=∠CED.
(1)求证:AD=AE
(2)∠ABC=2∠EDC,求证:∠BAD=∠C
(3)在(2)的条件下,∠ABC=∠EAD=60°,直接写出BD与AD之间的关系.
2.已知:如图1,在Rt△ABC中,∠ACB=90°,CA=CB.过点C作直线CP,点A关于直线CP的对称点为E,连接AE、BE,直线BE交直线CP于点F
(1)若∠PCA=18°,则∠CBF=_______°
(2)若90°<∠PCA<180°,在备选图中补全图形,用等式表示等式AC、BF、EF之间的数量关系,并证明
3.如图,在△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交△ABC的外角∠ACD的平分线于点F.
(1)探究线段OE与OF的数量关系并说明理由.
(2)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?请说明理由.
(3)当点O在边AC上运动时,四边形BCFE _____是菱形(填“可能”或“不可能”).请说明理由.
4.如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连接EF交CD于点M,连接AM.
(1)求证:EF=AC.
(2)若∠BAC=45°,求线段AM、DM、BC之间的数量关系.
类型六、等腰三角形实践与探究
例6.综合与实践:
初步认识筝形后,实践小组动手制作了一个“筝形功能器”,如图,在筝形ABCD中,AB=AD,CB=CD.
(1)【操作应用】如图1,将“筝形功能器”上的点与的顶点重合,分别放置在角的两边上,并过点画射线,求证:是的平分线;
(2)【实践拓展】实践小组尝试使用“筝形功能器”检测教室门框是否水平.如图2,在仪器上的点处栓一条线绳,线绳另一端挂一个铅锤,仪器上的点紧贴门框上方,观察发现线绳恰好经过点,即判断门框是水平的.实践小组的判断对吗?请说明理由.
针对练习6
1.
(1)问题发现:如图①,把一块三角板(AB=BC,∠ABC=90°)放入一个“U”形槽中,使三角形的三个顶点A、B、C分别在槽的两壁及底边上滑动,已知∠D=∠E=90°,在滑动过程中,发现与∠DAB始终相等的角是 ,与线段AD相等的线段是 .
(2)拓展探究:如图②,在△ABC中,点D在边BC上,并且DA=DE,∠B=∠ADE=∠C.求证:△ADB≌△DEC.
(3)能力提升:如图③,在等边△DEF中,A,C分别为DE、DF边上的点,AE=4,连接AC,以AC为边在△DEF内作等边△ABC,连接BF,当∠CFB=30°时,请求出CD的长度.
2.
(1)【问题情境】课外兴趣小组活动时,老师提出了如下问题:
如图1,是的中点,,,A,三点共线.
求证:.
小明在组内经过合作交流,得到解决方法:延长至点,使得,连结.
请根据小明的方法思考:由已知和作图能得到,依据是( )
A. B. C. D.
(2)由全等三角形、等腰三角形的性质可得.
【初步运用】如图2,在中,平分,为的中点,过点作,分别交的延长线和于点、点A.求证:.
(3)【拓展运用】如图3,在(1)的基础上(即是的中点,,,A,三点共线),连结,若,当,时,求的长.
人教版八年级数学上名师点拨精练
轴对称
专题 等腰三角形中的常见证明思路
类型一、利用等腰三角形的性质证明角相等
例1. 如图,在△ABC中,是的中点,,,垂足分别是、,且.
(1)求证:.
(2)连接AD,求证:AD⊥BC.
【答案】(1)证明:是的中点,
,
,,
,
在Rt和中,
,
≌
;
(2)解:,
,
△ABC是等腰三角形,
是的中点,
是△ABC底边上的中线,
也是△ABC底边上的高, 即AD⊥BC
针对练习1
1.如图,在△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
(1)求证:△ABE≌△DCE;
(2)求证:∠EBC=∠ECB.
【答案】(1)证明:在△ABE和△DCE中,
,
∴△ABE≌△DCE(AAS)
(2)证明:∵△ABE≌△DCE,
∴EB=EC,
∴△EBC是等腰三角形,
∴∠EBC=∠ECB.
2. 在△ABC中,AB<AC,AD为△ABC的角平分线,点E是BC边的中点.过点E作AD延长线的垂线,垂足为点G,交AC于点F,交AB的延长线于点H.
(1)求证:∠AHF=∠AFH;
(2)探究:在线段EH上是否能找到一点P,使得△BEP≌△CEF.如果能够,请找出并证明之;
(3)证明:BH=CF.
【答案】(1)证明:∵AD为△ABC的角平分线,
∴∠HAG=∠FAG,
∵FH⊥AD,
∴∠AGH=∠AGF=90°,
在△AHG和△AFG中,
,
∴△AHG≌△AFG(ASA),
∴∠AHF=∠AFH.
(2)解:在线段EH上能找到一点P,使得△BEP≌△CEF,理由如下:
作BP∥AC,交EH于点P,则△BEP≌△CEF,
证明:∵点E是BC边的中点,
∴BE=CE,
∵BP∥AC,
∴∠EBP=∠C,
在△BEP和△CEF中,
,
∴△BEP≌△CEF(ASA);
(3)证明:∵△BEP≌△CEF,
∴BP=CF,
∵BP∥AC,
∴∠BPH=∠AFH,
∵∠AHF=∠AFH,
∴∠BPH=∠AHF,
∴BH=BP,
∴BH=CF.
3.如图,BC⊥CA,BC=CA,DC⊥CE,DC=CE,直线BD与AE交于点F,交AC于点G,连接CF.
(1)求证:△ACE≌△BCD;
(2)求证:BF⊥AE;
(3)请判断∠CFE与∠CAB的大小关系并说明理由.
【答案】(1)证明:∵ BC⊥CA,DC⊥CE,
∴∠BCA=∠DCE=90°,
∴∠BCA-∠DCA=∠DCE-∠DCA
∴∠BCD=∠ACE.
在△BCD和△ACE中,
∴△BCD≌△ACE(SAS).
(2)证明:∵△BCD≌△ACE,
∴∠CBD=∠CAE.
∵∠BCA=90°,
∴∠CBA+∠CAB=90°.
∵∠CBA=∠CBD+∠DBA=∠CAE+∠DBA
∴∠CAE+∠DBA+∠CAB=∠DBA+∠BAE=90°.
∴ BF⊥AE .
(3)解:∠CFE=∠CAB,理由如下:
过C作CH⊥AE交延长线于点H,CI⊥BF于点I,
∵△BCD≌△ACE,
∴BD=AE,S△BCD=S△ACE,
∴CH=CI,
∴CF平分∠BFH,
BF⊥AE,
∴∠BFH=90°,∠CFE=45°.
∵BC⊥CA,BC=CA,
∴△ABC是等腰直角三角形,
∴∠CAB=45°,
∴∠CFE=∠CAB.
类型二、利用“三线合一”证明两线垂直
例2.如图,在中,,,试说明的理由.
解:已知,
▲
已知,
等式性质,
在与中,
,
≌ ,
,
又,
【答案】解:(已知),
(等边对等角),
(已知),
(等式性质),
(等角对等边),
在ABD与ACD中,
,(全等三角形的对应角相等),
又,
(等腰三角形的三线合一).
针对练习2
1. 如图,在△ABC中,是的中点,,,垂足分别是、,且.
(1)求证:.
(2)连接AD,求证:AD⊥BC.
【答案】(1)证明:是的中点,
,
,,
,
在Rt和中,
,
≌
;
(2)解:,
,
△ABC是等腰三角形,
是的中点,
是△ABC底边上的中线,
也是△ABC底边上的高, 即AD⊥BC
2.如图,在四边形中,,对角线与相交于点O,M、N分别是边、的中点.
(1)求证:;
(2)当,,时,求的长.
【答案】(1)解:证明:如图,连接.
,点M、点N分别是边、的中点,
∴,,
∴,
∵N是的中点,
∴是的垂直平分线,
.
(2)解:,,
,
,
,
,
,,
,
在中,,
∴cm,
答:的长是.
3.如图,在中,,过点作线段,连接,且满足.取的中点,连接.
(1)若,直接写出的取值范围 ;
(2)求证:.
【答案】(1)
(2)证明:,
,
.
为等腰三角形,
,
,
.
类型三、利用平行线证明等腰三角形
例3.如图,在平行四边形ABCD中,BCD的平分线与BA的延长线相交于点E,求证:BE=BC.
【答案】证明:∵四边形ABCD为平行四边形
∴BE//CD,
∴,
∵的平分线与BA的延长线相交于点E,
∴,
∴
∴BE=BC.
针对练习3
1.如图,在△ABC中,点D为边AC上的一点,BD=BC,过点D作DE∥AB交BC于点E,且 DE平分∠BDC.
求证:AD=BC.
【答案】证明:∵DE平分∠BDC,
∴∠BDE=∠CDE,
又∵DE∥AB,
∴∠BDE=∠ABD,∠CDE=∠A,
∴∠ABD=∠A,
∴AD=BD ,
∵BD=BC,
∴AD=BC.
2.如图,AD∥BC,BD平分∠ABC.求证:AB=AD.
【答案】证明:∵AD∥BC,∴∠ADB=∠DBC.
∵BD平分∠ABC,∴∠ABD=∠DBC.
∴∠ABD=∠ADB.∴AB=AD.
3.如图所示,在四边形ABCD中,的平分线与的平分线相交于点F,与的延长线交于点E,连接.
求证:
(1)是等腰三角形.
(2)若.则________.
【答案】(1)证明:∵平分
∴
∵
∴
∴
∴
∴ 是等腰三角形.
(2)7
5.
(1)如图,中,,,的平分线交于点,过点作交,于点,图中有 个等腰三角形猜想:与,之间有怎样的关系,并说明理由;
(2)如图,若,其他条件不变,图中有 个等腰三角形;与,间的关系是 ;
(3)如图,,若的角平分线与外角的角平分线交于点,过点作交于,交于图中有 个等腰三角形与,间的数量关系是 .
【答案】(1)
(2);
(3);
类型四、利用全等三角形证明等腰三角形
例4.如图所示,AE=AD,∠B=∠C,BE=4,AD=5,则AC=_____.
【答案】9
【解析】根据AAS证明△ABD与△ACE全等,再利用全等三角形的性质解答即可.
解:在△ABD与△ACE中,
,
∴△ABD≌△ACE(AAS),
∴AD=AE=5,AC=AB,
∴AC=AE+BE=4+5=9.
故答案为:9.
针对练习4
1.已知:如图,在等腰梯形ABCD中,AD∥BC,∠BDC=∠BCD,点E是线段BD上一点,且BE=AD.
(1)证明:△ADB≌△EBC;
(2)直接写出图中所有的等腰三角形.
【解析】(1)根据平行线的性质判定∠ADB=∠EBC,然后由∠BDC=∠BCD,得出BD=BC,结合BE=AD,利用SAS可证明结论;
(2)根据(1)的结论,可得CE=AB,结合等腰梯形的性质,可写出等腰三角形.
解(1)∵AD∥BC,
∴∠ADB=∠EBC,
∵∠BDC=∠BCD,
∴BD=BC,
在△ADB和△EBC中,
∴△ADB≌△EBC(SAS).
(2)由(1)可得△BCD是等腰三角形;
∵△ADB≌△EBC,
∴CE=AB,
又∵AB=CD,
∴CE=CD,
∴△CDE是等腰三角形.
2.从①∠B=∠C;②∠BAD=∠CDA;③AB=DC;④BE=CE四个等式中选出两个作为条件,证明△AED是等腰三角形(写出一种即可).已知:_____(只填序号)
求证:△AED是等腰三角形.
证明:
_____.
【答案】(1)①②(或①③,①④,②③);(2)在△BAD和△CDA中,
∵,
∴△BAD≌△CDA(AAS),
∴∠ADB=∠DAC,
即在△AED中∠ADE=∠DAE,
∴AE=DE,△AED为等腰三角形.;
【解析】首先选择条件证得△BAD≌△CDA,再利用全等三角形的性质得出∠ADB=∠DAC,即得出∠ADE=∠DAE,利用等腰三角形的判定定理可得结论.
解:选择的条件是:①∠B=∠C ②∠BAD=∠CDA(或①③,①④,②③);
证明:在△BAD和△CDA中,
∵,
∴△BAD≌△CDA(AAS),
∴∠ADB=∠DAC,
即 在△AED中∠ADE=∠DAE,
∴AE=DE,△AED为等腰三角形.
故答案为:在△BAD和△CDA中,
∵,
∴△BAD≌△CDA(AAS),
∴∠ADB=∠DAC,
即 在△AED中∠ADE=∠DAE,
∴AE=DE,△AED为等腰三角形.
3.如图,在△ABC中,已知点D在线段AB的反向延长线上,过AC的中点F作线段GE交∠DAC的平分线于E,交BC于G,且AE∥BC.
(1)求证:△ABC是等腰三角形.
(2)若AE=8,AB=10,GC=2BG,求△ABC的周长.
【解析】(1)首先依据平行线的性质证明∠B=∠DAE,∠C=∠CAE,然后结合角平分线的定义可证明∠B=∠C,故此可证明△ABC为等腰三角形;
(2)首先证明△AEF≌△CFG,从而得到CG的长,然后可求得BC的长,于是可求得△ABC的周长.
证明:(1)∵AE∥BC,
∴∠B=∠DAE,∠C=∠CAE.
∵AE平分∠DAC,
∴∠DAE=∠CAE.
∴∠B=∠C.
∴AB=AC.
∴△ABC是等腰三角形.
(2)∵F是AC的中点,
∴AF=CF.
∵AE∥BC,
∴∠C=∠CAE.
由对顶角相等可知:∠AFE=∠GFC.
在△AFE和△CFG中,
∴△AFE≌△CFG.
∴AE=GC=8.
∵GC=2BG,
∴BG=4.
∴BC=12.
∴△ABC的周长=AB+AC+BC=10+10+12=32.
4.已知:如图,AB=DC,BD=CA,求证:△AED是等腰三角形.
【解析】根据全等三角形的“SSS”判定定理证得△ABD≌△DCA,根据全等三角形的性质、等腰三角形的判定即可证得结论.
证明:在△ABD和△DCA中,
,
∴△ABD≌△DCA(SSS),
∴∠ADB=∠DAC,
∴EA=ED,
即△AED是等腰三角形.
类型五、等腰三角形中的探究问题
例5.如图,.
(1)写出与的数量关系
(2)延长到,使,延长到,使,连接.求证:.
(3)在(2)的条件下,作的平分线,交于点,求证:.
【答案】(1),
(2)见解析 (3)见解析
【解析】(1)勾股定理求得,结合已知条件即可求解;
(2)根据题意画出图形,证明,得出,则,即可得证;
(3)延长交于点,延长交于点,根据角平分线以及平行线的性质证明,进而证明,即可得证.
【小问1详解】
解:∵
∴,
∵
∴
即;
【小问2详解】
证明:如图所示,
∴
∴,
∵,
∴
∵,,
∴
∴
∴
∴
【小问3详解】
证明:如图所示,延长交于点,延长交于点,
∵,,
∴,
∴
∵是的角平分线,
∴,
∴
∴
∵,
∴,,
∴,
又∵,
∴,
即,
∴,
又,则,
在中,
,
∴,
∴
【点睛】本题考查了全等三角形的性质与判定,等腰三角形的性质与判定,勾股定理,平行线的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键.
针对练习5
1.如图,在△ABC中,点D、E分别在BC、AC上,连接AD、DE,∠ADB+∠EDC=∠CED.
(1)求证:AD=AE
(2)∠ABC=2∠EDC,求证:∠BAD=∠C
(3)在(2)的条件下,∠ABC=∠EAD=60°,直接写出BD与AD之间的关系.
【答案】(1)见解析 (2)见解析
(3)结论:AD=BD,证明见解析
【解析】(1)证明∠ADE=∠AED即可得到AD=AE;
(2)设∠CDE=x,则∠ABC=2∠EDC=2x,利用三角形的外角的性质解决问题;
(3)证明△ADE是等边三角形,得到∠ADE=60°,再证明∠ADB=90°,推出AB=2BD,再根据勾股定理得到4BD2=AD2+BD2,从而证明结论.
【小问1详解】
解:证明:∵∠ADB+∠EDC+∠ADE=180°,∠DEC+∠AED=180°,
又∵∠ADB+∠EDC=∠CED,
∴∠ADE=∠AED,
∴AD=AE;
【小问2详解】
证明:设∠CDE=x,则∠ABC=2∠EDC=2x,
∵∠ADE=∠AEC=∠EDC+∠C=x+∠C,
∴∠ADC=∠ADE+∠EDC=∠B+∠BAD,
∴∠C+∠EDC+∠EDC=∠B+∠BAD,
∴∠C+2x=2x+∠BAD,
∴∠BAD=∠C;
【小问3详解】
AD=BD,
理由:如图,
∵AD=AE,∠EAD=60°,
∴△ADE是等边三角形,
∴∠ADE=60°,
∵∠B=2∠EDC=60°,
∴∠EDC=30°,
∴∠ADC=∠ADB=90°,
∴∠BAD=30°,
∴AB=2BD,
∵AB2=AD2+BD2,
∴4BD2=AD2+BD2,
∴AD=BD.
【点睛】本题属于三角形综合题,考查了等腰三角形的判定和性质,三角形内角和定理,直角三角形30°的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
2.已知:如图1,在Rt△ABC中,∠ACB=90°,CA=CB.过点C作直线CP,点A关于直线CP的对称点为E,连接AE、BE,直线BE交直线CP于点F
(1)若∠PCA=18°,则∠CBF=_______°
(2)若90°<∠PCA<180°,在备选图中补全图形,用等式表示等式AC、BF、EF之间的数量关系,并证明
【答案】(1)27 (2)EF2+BF2=2AC2,理由见解析.
【解析】(1)如图:连接CE,先证得AC=CE=BC、∠ECB=126°,然后根据等腰三角形的性质即可解答;
(2)先按要求补全图形,再证明∠AFB=90°,最后利用勾股定理即可证明结论.
【小问1详解】
解:如图:连接CE
∵A,E关于PC对称,
∴∠ACP=∠ECP=18°,CE=AC
∴∠ECA=36°
∵在Rt△ABC中,∠ACB=90°,CA=CB.
∴∠ECB=∠ECA +∠ACB=90°+36°=126°,CE=BC
∴∠CEB=(180°-126°)÷2=27°.
故答案为:27.
【小问2详解】
解: EF2+BF2=2AC2,理由如下:
设∠ACP=∠PCE=
∵∠ACE=360°-2,∠ECB=360°-2=90°=270°-2,
∵CA=CE=CB,
∴∠AEC=∠CAE=(180°-360° + 2)= -90°,∠CEB=∠CBE=(180°-270°+ 2)=-45°,
∴∠AEB=∠CEB-∠CEA=45°,
∵A,E关于CF对称,
∴FA=EF,
∴∠FAE=∠FEA=45°,
∴∠AFB=90°,
∴AF2+BF2=AB2=2AC2.
【点睛】本题考查轴对称变换、等腰三角形的判定和性质、三角形内角和定理等知识点,解题的关键是掌握轴对称变换的性质,学会利用参数构建方程解决问题.
3.如图,在△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交△ABC的外角∠ACD的平分线于点F.
(1)探究线段OE与OF的数量关系并说明理由.
(2)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?请说明理由.
(3)当点O在边AC上运动时,四边形BCFE _____是菱形(填“可能”或“不可能”).请说明理由.
【答案】不可能
【解析】(1)由直线MN∥BC,MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,易证得△OEC与△OFC是等腰三角形,则可证得OE=OF=OC;
(2)正方形的判定问题,AECF若是正方形,则必有对角线OA=OC,所以O为AC的中点,同样在△ABC中,当∠ACB=90°时,可满足其为正方形;
(3)菱形的判定问题,若使菱形,则必有四条边相等,对角线互相垂直.
解:(1)OE=OF.理由如下:
∵CE是∠ACB的角平分线,
∴∠ACE=∠BCE,
又∵MN∥BC,
∴∠NEC=∠ECB,
∴∠NEC=∠ACE,
∴OE=OC,
∵CF是∠BCA的外角平分线,
∴∠OCF=∠FCD,
又∵MN∥BC,
∴∠OFC=∠FCD,
∴∠OFC=∠OCF,
∴OF=OC,
∴OE=OF;
(2)当点O运动到AC的中点,且△ABC满足∠ACB为直角的直角三角形时,四边形AECF是正方形.理由如下:
∵当点O运动到AC的中点时,AO=CO,
又∵EO=FO,
∴四边形AECF是平行四边形,
∵FO=CO,
∴AO=CO=EO=FO,
∴AO+CO=EO+FO,即AC=EF,
∴四边形AECF是矩形.
已知MN∥BC,当∠ACB=90°,则
∠AOF=∠COE=∠COF=∠AOE=90°,
∴AC⊥EF,
∴四边形AECF是正方形;
(3)不可能.理由如下:
如图,∵CE平分∠ACB,CF平分∠ACD,
∴∠ECF=∠ACB+∠ACD=(∠ACB+∠ACD)=90°,
若四边形BCFE是菱形,则BF⊥EC,
但在△GFC中,不可能存在两个角为90°,所以不存在其为菱形.
故答案为不可能.
4.如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连接EF交CD于点M,连接AM.
(1)求证:EF=AC.
(2)若∠BAC=45°,求线段AM、DM、BC之间的数量关系.
【解析】(1)根据等腰三角形三线合一的性质可得CE⊥BD,再根据直角三角形斜边上的中线等于斜边的一半可得EF=AC;
(2)判断出△AEC是等腰直角三角形,根据等腰直角三角形的性质可得EF垂直平分AC,再根据线段垂直平分线上的点到两端点的距离相等可得AM=CM,然后求出CD=AM+DM,再等量代换即可得解.
(1)证明:∵CD=CB,点E为BD的中点,
∴CE⊥BD,
∵点F为AC的中点,
∴EF=AC;
(2)解:∵∠BAC=45°,CE⊥BD,
∴△AEC是等腰直角三角形,
∵点F为AC的中点,
∴EF垂直平分AC,
∴AM=CM,
∵CD=CM+DM=AM+DM,CD=CB,
∴BC=AM+DM.
类型六、等腰三角形实践与探究
例6.综合与实践:
初步认识筝形后,实践小组动手制作了一个“筝形功能器”,如图,在筝形ABCD中,AB=AD,CB=CD.
(1)【操作应用】如图1,将“筝形功能器”上的点与的顶点重合,分别放置在角的两边上,并过点画射线,求证:是的平分线;
(2)【实践拓展】实践小组尝试使用“筝形功能器”检测教室门框是否水平.如图2,在仪器上的点处栓一条线绳,线绳另一端挂一个铅锤,仪器上的点紧贴门框上方,观察发现线绳恰好经过点,即判断门框是水平的.实践小组的判断对吗?请说明理由.
【答案】(1)证明:在和中,
,
,
,
是的平分线;
(2)解:实践小组的判断对,理由如下:
是等腰三角形,,
由(1)知:平分,
,
是铅锤线,
是水平的.
门框是水平的.
实践小组的判断对.
针对练习6
1.
(1)问题发现:如图①,把一块三角板(AB=BC,∠ABC=90°)放入一个“U”形槽中,使三角形的三个顶点A、B、C分别在槽的两壁及底边上滑动,已知∠D=∠E=90°,在滑动过程中,发现与∠DAB始终相等的角是 ,与线段AD相等的线段是 .
(2)拓展探究:如图②,在△ABC中,点D在边BC上,并且DA=DE,∠B=∠ADE=∠C.求证:△ADB≌△DEC.
(3)能力提升:如图③,在等边△DEF中,A,C分别为DE、DF边上的点,AE=4,连接AC,以AC为边在△DEF内作等边△ABC,连接BF,当∠CFB=30°时,请求出CD的长度.
【答案】(1);
(2)证明:,,
,
在和中,
(3)解:如图,过B作BMI EF交DF于点M,
是等边三角形,
,
,
,
,
,
,
,
在和中,
,
,
,
,
,
,
.
2.
(1)【问题情境】课外兴趣小组活动时,老师提出了如下问题:
如图1,是的中点,,,A,三点共线.
求证:.
小明在组内经过合作交流,得到解决方法:延长至点,使得,连结.
请根据小明的方法思考:由已知和作图能得到,依据是( )
A. B. C. D.
(2)由全等三角形、等腰三角形的性质可得.
【初步运用】如图2,在中,平分,为的中点,过点作,分别交的延长线和于点、点A.求证:.
(3)【拓展运用】如图3,在(1)的基础上(即是的中点,,,A,三点共线),连结,若,当,时,求的长.
【答案】(1)B
(2)证明:延长至点,使得,连结,
,,
,
,,
,
,,
平分,
,
,
,
;
(3)解:延长至点,使得,连结,过点C作于点H,
设,则,
由(1)知,
,,
,
,
,
,
,
,
,
在中,
,
,
又,,
,
,
,
在中,
,
,
解得,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版八年级数学上名师点拨精练
轴对称
专题 等腰三角形中的常见证明思路
类型一、利用等腰三角形的性质证明角相等
例1. 如图,在△ABC中,是的中点,,,垂足分别是、,且.
(1)求证:.
(2)连接AD,求证:AD⊥BC.
针对练习1
1.如图,在△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
(1)求证:△ABE≌△DCE;
(2)求证:∠EBC=∠ECB.
2. 在△ABC中,AB<AC,AD为△ABC的角平分线,点E是BC边的中点.过点E作AD延长线的垂线,垂足为点G,交AC于点F,交AB的延长线于点H.
(1)求证:∠AHF=∠AFH;
(2)探究:在线段EH上是否能找到一点P,使得△BEP≌△CEF.如果能够,请找出并证明之;
(3)证明:BH=CF.
3.如图,BC⊥CA,BC=CA,DC⊥CE,DC=CE,直线BD与AE交于点F,交AC于点G,连接CF.
(1)求证:△ACE≌△BCD;
(2)求证:BF⊥AE;
(3)请判断∠CFE与∠CAB的大小关系并说明理由.
类型二、利用“三线合一”证明两线垂直
例2.如图,在中,,,试说明的理由.
解:已知,
▲
已知,
等式性质,
在与中,
,
≌ ,
,
又,
针对练习2
1. 如图,在△ABC中,是的中点,,,垂足分别是、,且.
(1)求证:.
(2)连接AD,求证:AD⊥BC.
2.如图,在四边形中,,对角线与相交于点O,M、N分别是边、的中点.
(1)求证:;
(2)当,,时,求的长.
3.如图,在中,,过点作线段,连接,且满足.取的中点,连接.
(1)若,直接写出的取值范围 ;
(2)求证:.
类型三、利用平行线证明等腰三角形
例3.如图,在平行四边形ABCD中,BCD的平分线与BA的延长线相交于点E,求证:BE=BC.
针对练习3
1.如图,在△ABC中,点D为边AC上的一点,BD=BC,过点D作DE∥AB交BC于点E,且 DE平分∠BDC.
求证:AD=BC.
2.如图,AD∥BC,BD平分∠ABC.求证:AB=AD.
3.如图所示,在四边形ABCD中,的平分线与的平分线相交于点F,与的延长线交于点E,连接.
求证:
(1)是等腰三角形.
(2)若.则________.
5.
(1)如图,中,,,的平分线交于点,过点作交,于点,图中有 个等腰三角形猜想:与,之间有怎样的关系,并说明理由;
(2)如图,若,其他条件不变,图中有 个等腰三角形;与,间的关系是 ;
(3)如图,,若的角平分线与外角的角平分线交于点,过点作交于,交于图中有 个等腰三角形与,间的数量关系是 .
类型四、利用全等三角形证明等腰三角形
例4.如图所示,AE=AD,∠B=∠C,BE=4,AD=5,则AC=_____.
针对练习4
1.已知:如图,在等腰梯形ABCD中,AD∥BC,∠BDC=∠BCD,点E是线段BD上一点,且BE=AD.
(1)证明:△ADB≌△EBC;
(2)直接写出图中所有的等腰三角形.
2.从①∠B=∠C;②∠BAD=∠CDA;③AB=DC;④BE=CE四个等式中选出两个作为条件,证明△AED是等腰三角形(写出一种即可).已知:_____(只填序号)
求证:△AED是等腰三角形.
证明:
_____.
3.如图,在△ABC中,已知点D在线段AB的反向延长线上,过AC的中点F作线段GE交∠DAC的平分线于E,交BC于G,且AE∥BC.
(1)求证:△ABC是等腰三角形.
(2)若AE=8,AB=10,GC=2BG,求△ABC的周长.
4.已知:如图,AB=DC,BD=CA,求证:△AED是等腰三角形.
类型五、等腰三角形中的探究问题
例5.如图,.
(1)写出与的数量关系
(2)延长到,使,延长到,使,连接.求证:.
(3)在(2)的条件下,作的平分线,交于点,求证:.
针对练习5
1.如图,在△ABC中,点D、E分别在BC、AC上,连接AD、DE,∠ADB+∠EDC=∠CED.
(1)求证:AD=AE
(2)∠ABC=2∠EDC,求证:∠BAD=∠C
(3)在(2)的条件下,∠ABC=∠EAD=60°,直接写出BD与AD之间的关系.
2.已知:如图1,在Rt△ABC中,∠ACB=90°,CA=CB.过点C作直线CP,点A关于直线CP的对称点为E,连接AE、BE,直线BE交直线CP于点F
(1)若∠PCA=18°,则∠CBF=_______°
(2)若90°<∠PCA<180°,在备选图中补全图形,用等式表示等式AC、BF、EF之间的数量关系,并证明
3.如图,在△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交△ABC的外角∠ACD的平分线于点F.
(1)探究线段OE与OF的数量关系并说明理由.
(2)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?请说明理由.
(3)当点O在边AC上运动时,四边形BCFE _____是菱形(填“可能”或“不可能”).请说明理由.
4.如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连接EF交CD于点M,连接AM.
(1)求证:EF=AC.
(2)若∠BAC=45°,求线段AM、DM、BC之间的数量关系.
类型六、等腰三角形实践与探究
例6.综合与实践:
初步认识筝形后,实践小组动手制作了一个“筝形功能器”,如图,在筝形ABCD中,AB=AD,CB=CD.
(1)【操作应用】如图1,将“筝形功能器”上的点与的顶点重合,分别放置在角的两边上,并过点画射线,求证:是的平分线;
(2)【实践拓展】实践小组尝试使用“筝形功能器”检测教室门框是否水平.如图2,在仪器上的点处栓一条线绳,线绳另一端挂一个铅锤,仪器上的点紧贴门框上方,观察发现线绳恰好经过点,即判断门框是水平的.实践小组的判断对吗?请说明理由.
针对练习6
1.
(1)问题发现:如图①,把一块三角板(AB=BC,∠ABC=90°)放入一个“U”形槽中,使三角形的三个顶点A、B、C分别在槽的两壁及底边上滑动,已知∠D=∠E=90°,在滑动过程中,发现与∠DAB始终相等的角是 ,与线段AD相等的线段是 .
(2)拓展探究:如图②,在△ABC中,点D在边BC上,并且DA=DE,∠B=∠ADE=∠C.求证:△ADB≌△DEC.
(3)能力提升:如图③,在等边△DEF中,A,C分别为DE、DF边上的点,AE=4,连接AC,以AC为边在△DEF内作等边△ABC,连接BF,当∠CFB=30°时,请求出CD的长度.
2.
(1)【问题情境】课外兴趣小组活动时,老师提出了如下问题:
如图1,是的中点,,,A,三点共线.
求证:.
小明在组内经过合作交流,得到解决方法:延长至点,使得,连结.
请根据小明的方法思考:由已知和作图能得到,依据是( )
A. B. C. D.
(2)由全等三角形、等腰三角形的性质可得.
【初步运用】如图2,在中,平分,为的中点,过点作,分别交的延长线和于点、点A.求证:.
(3)【拓展运用】如图3,在(1)的基础上(即是的中点,,,A,三点共线),连结,若,当,时,求的长.
人教版八年级数学上名师点拨精练
轴对称
专题 等腰三角形中的常见证明思路
类型一、利用等腰三角形的性质证明角相等
例1. 如图,在△ABC中,是的中点,,,垂足分别是、,且.
(1)求证:.
(2)连接AD,求证:AD⊥BC.
【答案】(1)证明:是的中点,
,
,,
,
在Rt和中,
,
≌
;
(2)解:,
,
△ABC是等腰三角形,
是的中点,
是△ABC底边上的中线,
也是△ABC底边上的高, 即AD⊥BC
针对练习1
1.如图,在△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
(1)求证:△ABE≌△DCE;
(2)求证:∠EBC=∠ECB.
【答案】(1)证明:在△ABE和△DCE中,
,
∴△ABE≌△DCE(AAS)
(2)证明:∵△ABE≌△DCE,
∴EB=EC,
∴△EBC是等腰三角形,
∴∠EBC=∠ECB.
2. 在△ABC中,AB<AC,AD为△ABC的角平分线,点E是BC边的中点.过点E作AD延长线的垂线,垂足为点G,交AC于点F,交AB的延长线于点H.
(1)求证:∠AHF=∠AFH;
(2)探究:在线段EH上是否能找到一点P,使得△BEP≌△CEF.如果能够,请找出并证明之;
(3)证明:BH=CF.
【答案】(1)证明:∵AD为△ABC的角平分线,
∴∠HAG=∠FAG,
∵FH⊥AD,
∴∠AGH=∠AGF=90°,
在△AHG和△AFG中,
,
∴△AHG≌△AFG(ASA),
∴∠AHF=∠AFH.
(2)解:在线段EH上能找到一点P,使得△BEP≌△CEF,理由如下:
作BP∥AC,交EH于点P,则△BEP≌△CEF,
证明:∵点E是BC边的中点,
∴BE=CE,
∵BP∥AC,
∴∠EBP=∠C,
在△BEP和△CEF中,
,
∴△BEP≌△CEF(ASA);
(3)证明:∵△BEP≌△CEF,
∴BP=CF,
∵BP∥AC,
∴∠BPH=∠AFH,
∵∠AHF=∠AFH,
∴∠BPH=∠AHF,
∴BH=BP,
∴BH=CF.
3.如图,BC⊥CA,BC=CA,DC⊥CE,DC=CE,直线BD与AE交于点F,交AC于点G,连接CF.
(1)求证:△ACE≌△BCD;
(2)求证:BF⊥AE;
(3)请判断∠CFE与∠CAB的大小关系并说明理由.
【答案】(1)证明:∵ BC⊥CA,DC⊥CE,
∴∠BCA=∠DCE=90°,
∴∠BCA-∠DCA=∠DCE-∠DCA
∴∠BCD=∠ACE.
在△BCD和△ACE中,
∴△BCD≌△ACE(SAS).
(2)证明:∵△BCD≌△ACE,
∴∠CBD=∠CAE.
∵∠BCA=90°,
∴∠CBA+∠CAB=90°.
∵∠CBA=∠CBD+∠DBA=∠CAE+∠DBA
∴∠CAE+∠DBA+∠CAB=∠DBA+∠BAE=90°.
∴ BF⊥AE .
(3)解:∠CFE=∠CAB,理由如下:
过C作CH⊥AE交延长线于点H,CI⊥BF于点I,
∵△BCD≌△ACE,
∴BD=AE,S△BCD=S△ACE,
∴CH=CI,
∴CF平分∠BFH,
BF⊥AE,
∴∠BFH=90°,∠CFE=45°.
∵BC⊥CA,BC=CA,
∴△ABC是等腰直角三角形,
∴∠CAB=45°,
∴∠CFE=∠CAB.
类型二、利用“三线合一”证明两线垂直
例2.如图,在中,,,试说明的理由.
解:已知,
▲
已知,
等式性质,
在与中,
,
≌ ,
,
又,
【答案】解:(已知),
(等边对等角),
(已知),
(等式性质),
(等角对等边),
在ABD与ACD中,
,(全等三角形的对应角相等),
又,
(等腰三角形的三线合一).
针对练习2
1. 如图,在△ABC中,是的中点,,,垂足分别是、,且.
(1)求证:.
(2)连接AD,求证:AD⊥BC.
【答案】(1)证明:是的中点,
,
,,
,
在Rt和中,
,
≌
;
(2)解:,
,
△ABC是等腰三角形,
是的中点,
是△ABC底边上的中线,
也是△ABC底边上的高, 即AD⊥BC
2.如图,在四边形中,,对角线与相交于点O,M、N分别是边、的中点.
(1)求证:;
(2)当,,时,求的长.
【答案】(1)解:证明:如图,连接.
,点M、点N分别是边、的中点,
∴,,
∴,
∵N是的中点,
∴是的垂直平分线,
.
(2)解:,,
,
,
,
,
,,
,
在中,,
∴cm,
答:的长是.
3.如图,在中,,过点作线段,连接,且满足.取的中点,连接.
(1)若,直接写出的取值范围 ;
(2)求证:.
【答案】(1)
(2)证明:,
,
.
为等腰三角形,
,
,
.
类型三、利用平行线证明等腰三角形
例3.如图,在平行四边形ABCD中,BCD的平分线与BA的延长线相交于点E,求证:BE=BC.
【答案】证明:∵四边形ABCD为平行四边形
∴BE//CD,
∴,
∵的平分线与BA的延长线相交于点E,
∴,
∴
∴BE=BC.
针对练习3
1.如图,在△ABC中,点D为边AC上的一点,BD=BC,过点D作DE∥AB交BC于点E,且 DE平分∠BDC.
求证:AD=BC.
【答案】证明:∵DE平分∠BDC,
∴∠BDE=∠CDE,
又∵DE∥AB,
∴∠BDE=∠ABD,∠CDE=∠A,
∴∠ABD=∠A,
∴AD=BD ,
∵BD=BC,
∴AD=BC.
2.如图,AD∥BC,BD平分∠ABC.求证:AB=AD.
【答案】证明:∵AD∥BC,∴∠ADB=∠DBC.
∵BD平分∠ABC,∴∠ABD=∠DBC.
∴∠ABD=∠ADB.∴AB=AD.
3.如图所示,在四边形ABCD中,的平分线与的平分线相交于点F,与的延长线交于点E,连接.
求证:
(1)是等腰三角形.
(2)若.则________.
【答案】(1)证明:∵平分
∴
∵
∴
∴
∴
∴ 是等腰三角形.
(2)7
5.
(1)如图,中,,,的平分线交于点,过点作交,于点,图中有 个等腰三角形猜想:与,之间有怎样的关系,并说明理由;
(2)如图,若,其他条件不变,图中有 个等腰三角形;与,间的关系是 ;
(3)如图,,若的角平分线与外角的角平分线交于点,过点作交于,交于图中有 个等腰三角形与,间的数量关系是 .
【答案】(1)
(2);
(3);
类型四、利用全等三角形证明等腰三角形
例4.如图所示,AE=AD,∠B=∠C,BE=4,AD=5,则AC=_____.
【答案】9
【解析】根据AAS证明△ABD与△ACE全等,再利用全等三角形的性质解答即可.
解:在△ABD与△ACE中,
,
∴△ABD≌△ACE(AAS),
∴AD=AE=5,AC=AB,
∴AC=AE+BE=4+5=9.
故答案为:9.
针对练习4
1.已知:如图,在等腰梯形ABCD中,AD∥BC,∠BDC=∠BCD,点E是线段BD上一点,且BE=AD.
(1)证明:△ADB≌△EBC;
(2)直接写出图中所有的等腰三角形.
【解析】(1)根据平行线的性质判定∠ADB=∠EBC,然后由∠BDC=∠BCD,得出BD=BC,结合BE=AD,利用SAS可证明结论;
(2)根据(1)的结论,可得CE=AB,结合等腰梯形的性质,可写出等腰三角形.
解(1)∵AD∥BC,
∴∠ADB=∠EBC,
∵∠BDC=∠BCD,
∴BD=BC,
在△ADB和△EBC中,
∴△ADB≌△EBC(SAS).
(2)由(1)可得△BCD是等腰三角形;
∵△ADB≌△EBC,
∴CE=AB,
又∵AB=CD,
∴CE=CD,
∴△CDE是等腰三角形.
2.从①∠B=∠C;②∠BAD=∠CDA;③AB=DC;④BE=CE四个等式中选出两个作为条件,证明△AED是等腰三角形(写出一种即可).已知:_____(只填序号)
求证:△AED是等腰三角形.
证明:
_____.
【答案】(1)①②(或①③,①④,②③);(2)在△BAD和△CDA中,
∵,
∴△BAD≌△CDA(AAS),
∴∠ADB=∠DAC,
即在△AED中∠ADE=∠DAE,
∴AE=DE,△AED为等腰三角形.;
【解析】首先选择条件证得△BAD≌△CDA,再利用全等三角形的性质得出∠ADB=∠DAC,即得出∠ADE=∠DAE,利用等腰三角形的判定定理可得结论.
解:选择的条件是:①∠B=∠C ②∠BAD=∠CDA(或①③,①④,②③);
证明:在△BAD和△CDA中,
∵,
∴△BAD≌△CDA(AAS),
∴∠ADB=∠DAC,
即 在△AED中∠ADE=∠DAE,
∴AE=DE,△AED为等腰三角形.
故答案为:在△BAD和△CDA中,
∵,
∴△BAD≌△CDA(AAS),
∴∠ADB=∠DAC,
即 在△AED中∠ADE=∠DAE,
∴AE=DE,△AED为等腰三角形.
3.如图,在△ABC中,已知点D在线段AB的反向延长线上,过AC的中点F作线段GE交∠DAC的平分线于E,交BC于G,且AE∥BC.
(1)求证:△ABC是等腰三角形.
(2)若AE=8,AB=10,GC=2BG,求△ABC的周长.
【解析】(1)首先依据平行线的性质证明∠B=∠DAE,∠C=∠CAE,然后结合角平分线的定义可证明∠B=∠C,故此可证明△ABC为等腰三角形;
(2)首先证明△AEF≌△CFG,从而得到CG的长,然后可求得BC的长,于是可求得△ABC的周长.
证明:(1)∵AE∥BC,
∴∠B=∠DAE,∠C=∠CAE.
∵AE平分∠DAC,
∴∠DAE=∠CAE.
∴∠B=∠C.
∴AB=AC.
∴△ABC是等腰三角形.
(2)∵F是AC的中点,
∴AF=CF.
∵AE∥BC,
∴∠C=∠CAE.
由对顶角相等可知:∠AFE=∠GFC.
在△AFE和△CFG中,
∴△AFE≌△CFG.
∴AE=GC=8.
∵GC=2BG,
∴BG=4.
∴BC=12.
∴△ABC的周长=AB+AC+BC=10+10+12=32.
4.已知:如图,AB=DC,BD=CA,求证:△AED是等腰三角形.
【解析】根据全等三角形的“SSS”判定定理证得△ABD≌△DCA,根据全等三角形的性质、等腰三角形的判定即可证得结论.
证明:在△ABD和△DCA中,
,
∴△ABD≌△DCA(SSS),
∴∠ADB=∠DAC,
∴EA=ED,
即△AED是等腰三角形.
类型五、等腰三角形中的探究问题
例5.如图,.
(1)写出与的数量关系
(2)延长到,使,延长到,使,连接.求证:.
(3)在(2)的条件下,作的平分线,交于点,求证:.
【答案】(1),
(2)见解析 (3)见解析
【解析】(1)勾股定理求得,结合已知条件即可求解;
(2)根据题意画出图形,证明,得出,则,即可得证;
(3)延长交于点,延长交于点,根据角平分线以及平行线的性质证明,进而证明,即可得证.
【小问1详解】
解:∵
∴,
∵
∴
即;
【小问2详解】
证明:如图所示,
∴
∴,
∵,
∴
∵,,
∴
∴
∴
∴
【小问3详解】
证明:如图所示,延长交于点,延长交于点,
∵,,
∴,
∴
∵是的角平分线,
∴,
∴
∴
∵,
∴,,
∴,
又∵,
∴,
即,
∴,
又,则,
在中,
,
∴,
∴
【点睛】本题考查了全等三角形的性质与判定,等腰三角形的性质与判定,勾股定理,平行线的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键.
针对练习5
1.如图,在△ABC中,点D、E分别在BC、AC上,连接AD、DE,∠ADB+∠EDC=∠CED.
(1)求证:AD=AE
(2)∠ABC=2∠EDC,求证:∠BAD=∠C
(3)在(2)的条件下,∠ABC=∠EAD=60°,直接写出BD与AD之间的关系.
【答案】(1)见解析 (2)见解析
(3)结论:AD=BD,证明见解析
【解析】(1)证明∠ADE=∠AED即可得到AD=AE;
(2)设∠CDE=x,则∠ABC=2∠EDC=2x,利用三角形的外角的性质解决问题;
(3)证明△ADE是等边三角形,得到∠ADE=60°,再证明∠ADB=90°,推出AB=2BD,再根据勾股定理得到4BD2=AD2+BD2,从而证明结论.
【小问1详解】
解:证明:∵∠ADB+∠EDC+∠ADE=180°,∠DEC+∠AED=180°,
又∵∠ADB+∠EDC=∠CED,
∴∠ADE=∠AED,
∴AD=AE;
【小问2详解】
证明:设∠CDE=x,则∠ABC=2∠EDC=2x,
∵∠ADE=∠AEC=∠EDC+∠C=x+∠C,
∴∠ADC=∠ADE+∠EDC=∠B+∠BAD,
∴∠C+∠EDC+∠EDC=∠B+∠BAD,
∴∠C+2x=2x+∠BAD,
∴∠BAD=∠C;
【小问3详解】
AD=BD,
理由:如图,
∵AD=AE,∠EAD=60°,
∴△ADE是等边三角形,
∴∠ADE=60°,
∵∠B=2∠EDC=60°,
∴∠EDC=30°,
∴∠ADC=∠ADB=90°,
∴∠BAD=30°,
∴AB=2BD,
∵AB2=AD2+BD2,
∴4BD2=AD2+BD2,
∴AD=BD.
【点睛】本题属于三角形综合题,考查了等腰三角形的判定和性质,三角形内角和定理,直角三角形30°的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
2.已知:如图1,在Rt△ABC中,∠ACB=90°,CA=CB.过点C作直线CP,点A关于直线CP的对称点为E,连接AE、BE,直线BE交直线CP于点F
(1)若∠PCA=18°,则∠CBF=_______°
(2)若90°<∠PCA<180°,在备选图中补全图形,用等式表示等式AC、BF、EF之间的数量关系,并证明
【答案】(1)27 (2)EF2+BF2=2AC2,理由见解析.
【解析】(1)如图:连接CE,先证得AC=CE=BC、∠ECB=126°,然后根据等腰三角形的性质即可解答;
(2)先按要求补全图形,再证明∠AFB=90°,最后利用勾股定理即可证明结论.
【小问1详解】
解:如图:连接CE
∵A,E关于PC对称,
∴∠ACP=∠ECP=18°,CE=AC
∴∠ECA=36°
∵在Rt△ABC中,∠ACB=90°,CA=CB.
∴∠ECB=∠ECA +∠ACB=90°+36°=126°,CE=BC
∴∠CEB=(180°-126°)÷2=27°.
故答案为:27.
【小问2详解】
解: EF2+BF2=2AC2,理由如下:
设∠ACP=∠PCE=
∵∠ACE=360°-2,∠ECB=360°-2=90°=270°-2,
∵CA=CE=CB,
∴∠AEC=∠CAE=(180°-360° + 2)= -90°,∠CEB=∠CBE=(180°-270°+ 2)=-45°,
∴∠AEB=∠CEB-∠CEA=45°,
∵A,E关于CF对称,
∴FA=EF,
∴∠FAE=∠FEA=45°,
∴∠AFB=90°,
∴AF2+BF2=AB2=2AC2.
【点睛】本题考查轴对称变换、等腰三角形的判定和性质、三角形内角和定理等知识点,解题的关键是掌握轴对称变换的性质,学会利用参数构建方程解决问题.
3.如图,在△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交△ABC的外角∠ACD的平分线于点F.
(1)探究线段OE与OF的数量关系并说明理由.
(2)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?请说明理由.
(3)当点O在边AC上运动时,四边形BCFE _____是菱形(填“可能”或“不可能”).请说明理由.
【答案】不可能
【解析】(1)由直线MN∥BC,MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,易证得△OEC与△OFC是等腰三角形,则可证得OE=OF=OC;
(2)正方形的判定问题,AECF若是正方形,则必有对角线OA=OC,所以O为AC的中点,同样在△ABC中,当∠ACB=90°时,可满足其为正方形;
(3)菱形的判定问题,若使菱形,则必有四条边相等,对角线互相垂直.
解:(1)OE=OF.理由如下:
∵CE是∠ACB的角平分线,
∴∠ACE=∠BCE,
又∵MN∥BC,
∴∠NEC=∠ECB,
∴∠NEC=∠ACE,
∴OE=OC,
∵CF是∠BCA的外角平分线,
∴∠OCF=∠FCD,
又∵MN∥BC,
∴∠OFC=∠FCD,
∴∠OFC=∠OCF,
∴OF=OC,
∴OE=OF;
(2)当点O运动到AC的中点,且△ABC满足∠ACB为直角的直角三角形时,四边形AECF是正方形.理由如下:
∵当点O运动到AC的中点时,AO=CO,
又∵EO=FO,
∴四边形AECF是平行四边形,
∵FO=CO,
∴AO=CO=EO=FO,
∴AO+CO=EO+FO,即AC=EF,
∴四边形AECF是矩形.
已知MN∥BC,当∠ACB=90°,则
∠AOF=∠COE=∠COF=∠AOE=90°,
∴AC⊥EF,
∴四边形AECF是正方形;
(3)不可能.理由如下:
如图,∵CE平分∠ACB,CF平分∠ACD,
∴∠ECF=∠ACB+∠ACD=(∠ACB+∠ACD)=90°,
若四边形BCFE是菱形,则BF⊥EC,
但在△GFC中,不可能存在两个角为90°,所以不存在其为菱形.
故答案为不可能.
4.如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连接EF交CD于点M,连接AM.
(1)求证:EF=AC.
(2)若∠BAC=45°,求线段AM、DM、BC之间的数量关系.
【解析】(1)根据等腰三角形三线合一的性质可得CE⊥BD,再根据直角三角形斜边上的中线等于斜边的一半可得EF=AC;
(2)判断出△AEC是等腰直角三角形,根据等腰直角三角形的性质可得EF垂直平分AC,再根据线段垂直平分线上的点到两端点的距离相等可得AM=CM,然后求出CD=AM+DM,再等量代换即可得解.
(1)证明:∵CD=CB,点E为BD的中点,
∴CE⊥BD,
∵点F为AC的中点,
∴EF=AC;
(2)解:∵∠BAC=45°,CE⊥BD,
∴△AEC是等腰直角三角形,
∵点F为AC的中点,
∴EF垂直平分AC,
∴AM=CM,
∵CD=CM+DM=AM+DM,CD=CB,
∴BC=AM+DM.
类型六、等腰三角形实践与探究
例6.综合与实践:
初步认识筝形后,实践小组动手制作了一个“筝形功能器”,如图,在筝形ABCD中,AB=AD,CB=CD.
(1)【操作应用】如图1,将“筝形功能器”上的点与的顶点重合,分别放置在角的两边上,并过点画射线,求证:是的平分线;
(2)【实践拓展】实践小组尝试使用“筝形功能器”检测教室门框是否水平.如图2,在仪器上的点处栓一条线绳,线绳另一端挂一个铅锤,仪器上的点紧贴门框上方,观察发现线绳恰好经过点,即判断门框是水平的.实践小组的判断对吗?请说明理由.
【答案】(1)证明:在和中,
,
,
,
是的平分线;
(2)解:实践小组的判断对,理由如下:
是等腰三角形,,
由(1)知:平分,
,
是铅锤线,
是水平的.
门框是水平的.
实践小组的判断对.
针对练习6
1.
(1)问题发现:如图①,把一块三角板(AB=BC,∠ABC=90°)放入一个“U”形槽中,使三角形的三个顶点A、B、C分别在槽的两壁及底边上滑动,已知∠D=∠E=90°,在滑动过程中,发现与∠DAB始终相等的角是 ,与线段AD相等的线段是 .
(2)拓展探究:如图②,在△ABC中,点D在边BC上,并且DA=DE,∠B=∠ADE=∠C.求证:△ADB≌△DEC.
(3)能力提升:如图③,在等边△DEF中,A,C分别为DE、DF边上的点,AE=4,连接AC,以AC为边在△DEF内作等边△ABC,连接BF,当∠CFB=30°时,请求出CD的长度.
【答案】(1);
(2)证明:,,
,
在和中,
(3)解:如图,过B作BMI EF交DF于点M,
是等边三角形,
,
,
,
,
,
,
,
在和中,
,
,
,
,
,
,
.
2.
(1)【问题情境】课外兴趣小组活动时,老师提出了如下问题:
如图1,是的中点,,,A,三点共线.
求证:.
小明在组内经过合作交流,得到解决方法:延长至点,使得,连结.
请根据小明的方法思考:由已知和作图能得到,依据是( )
A. B. C. D.
(2)由全等三角形、等腰三角形的性质可得.
【初步运用】如图2,在中,平分,为的中点,过点作,分别交的延长线和于点、点A.求证:.
(3)【拓展运用】如图3,在(1)的基础上(即是的中点,,,A,三点共线),连结,若,当,时,求的长.
【答案】(1)B
(2)证明:延长至点,使得,连结,
,,
,
,,
,
,,
平分,
,
,
,
;
(3)解:延长至点,使得,连结,过点C作于点H,
设,则,
由(1)知,
,,
,
,
,
,
,
,
,
在中,
,
,
又,,
,
,
,
在中,
,
,
解得,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
