人教版八年级数学上名师点拨精练第13章 轴对称13.4 最短路径问题(含解析)
文档属性
| 名称 | 人教版八年级数学上名师点拨精练第13章 轴对称13.4 最短路径问题(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-18 10:13:42 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版八年级数学上名师点拨精练
轴对称
13.4 最短路径问题
学习目标
1.能利用轴对称解决简单的最短路径问题。体会图形的变化在解诀最值问题中的作用。
2.感悟转化思想。
重点:利用轴对称将最短路径问题转化为“两点之间,线段最短”问题。
难点:路径最短的证明。
老师告诉你
1.最短路径问题的类型
(1)两点一线型的线段和的最小值问题;(2)两线一点型的线段和的最小值问题;(3)两点两线型的线段和的最小值问题。
2.解决最短路径问题的方法
借助轴对称或平移的知识,化折为直,利用两点之间线段最短或垂线段最短来求线段和的最小值。
知识点拨
知识点1 两点一线型
1.类型一 两定点在直线两侧,动点在直线上,求线段和最小值
求直线异侧的两点与直线上一点所连线段的和最小的问题,只要连接这两点,与直线的交点即为所求.
如图所示,点A,B分别是直线l异侧的两个点,在l上找一个点C,使CA+CB最短,这时点C是直线l与AB的交点.
2.类型二 两定点在直线同侧,动点在直线上,求线段和最小值
求直线同侧的两点与直线上一点所连线段的和最小的问题,只要找到其中一个点关于这条直线的对称点,连接对称点与另一个点,则与该直线的交点即为所求.
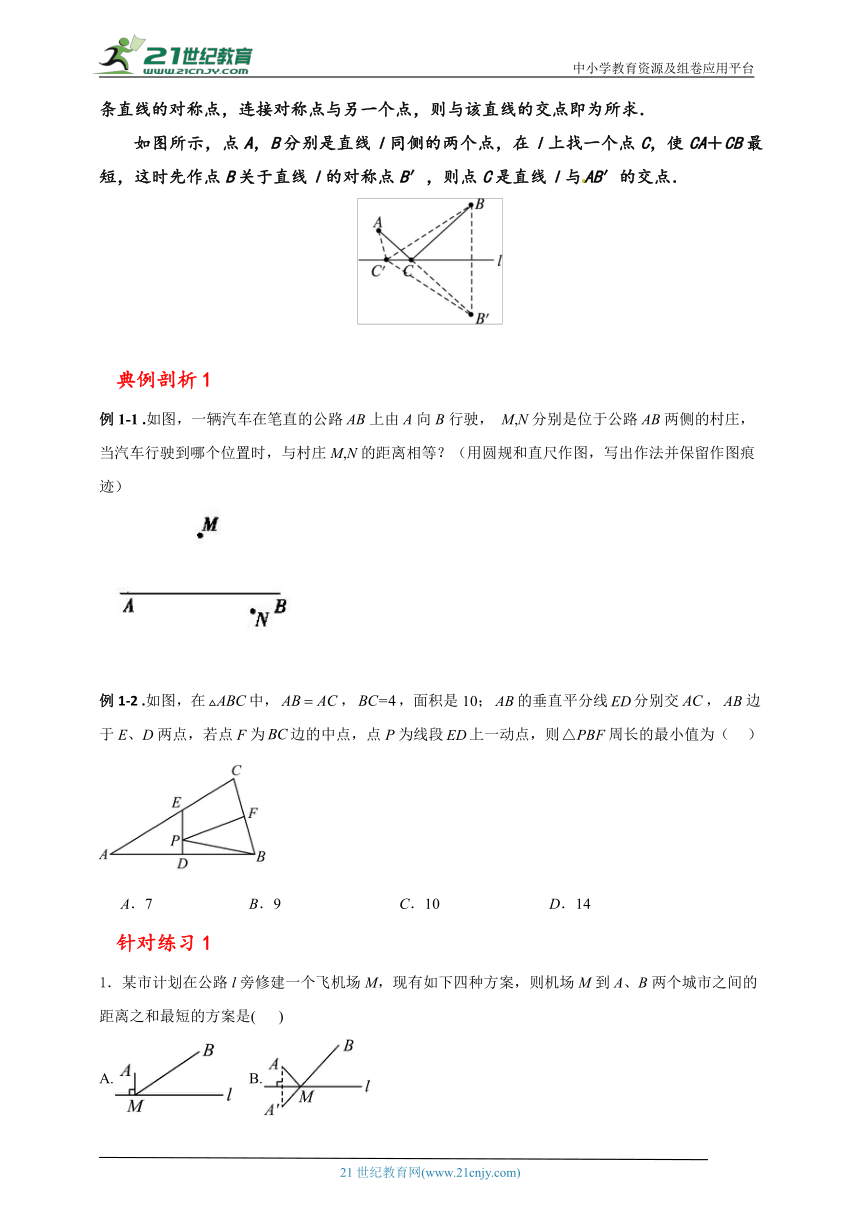
如图所示,点A,B分别是直线l同侧的两个点,在l上找一个点C,使CA+CB最短,这时先作点B关于直线l的对称点B′,则点C是直线l与AB′的交点.
典例剖析1
例1-1 .如图,一辆汽车在笔直的公路AB上由A向B行驶, M,N分别是位于公路AB两侧的村庄,当汽车行驶到哪个位置时,与村庄M,N的距离相等?(用圆规和直尺作图,写出作法并保留作图痕迹)
例1-2 .如图,在中,,,面积是10;的垂直平分线分别交,边于E、D两点,若点F为边的中点,点P为线段上一动点,则周长的最小值为( )
A.7 B.9 C.10 D.14
针对练习1
1.某市计划在公路l旁修建一个飞机场M,现有如下四种方案,则机场M到A、B两个城市之间的距离之和最短的方案是( )
A. B.
C. D.
2.如图,在正方形网格中有M,N两点,在直线l上求一点P,使最短,则点P应选在( )
A.A点 B.B点 C.C点 D.D点
3.如图,点A,B在直线l同侧,在直线l上取一点P,使得最小,对点P的位置叙述正确的是( )
A.作线段的垂直平分线与直线l的交点,即为点P
B.过点A作直线l的垂线,垂足即为点P
C.作点B关于直线l的对称点,连接,与直线的交点,即为点P
D.延长与直线l的交点,即为点P
4.在一条沿直线铺设的电缆一侧有P,Q两个小区,要求在直线l上的某处选取一点M,向P,Q两个小区铺设电缆,现有如下四种铺设方案,图中实线表示铺设的电缆,则所需电缆材料最短的是( )
A. B.
C. D.
知识点2 两线一点型
1.类型三 一定点在角内部,两动点在角的两边上,求线段和最小值
求角内部一点与角两边所在直线上的两点所构成的三角形周长最小的问题,只要分别找到角内部这个点关于角两边所在直线的对称点,连接对称点与角两边所在直线的交点,即为所求.
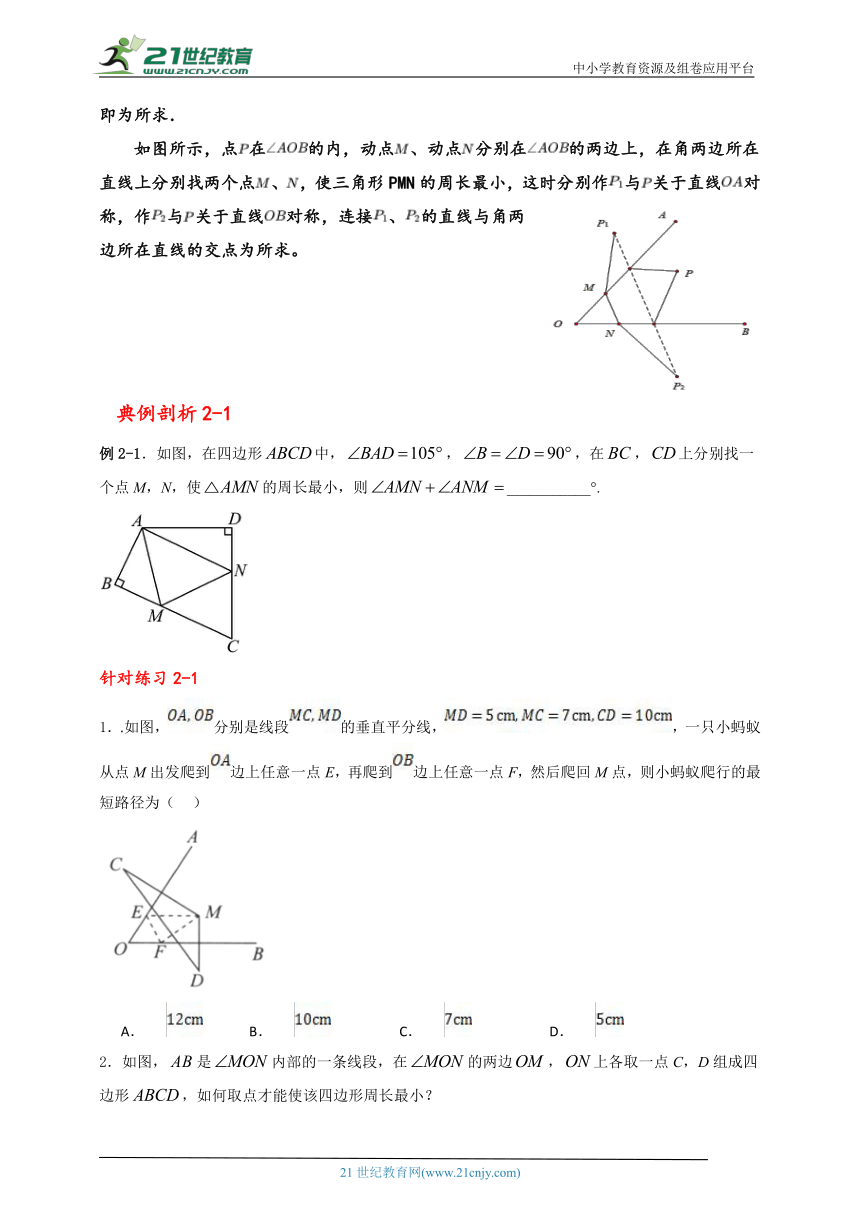
如图所示,点在的内,动点、动点分别在的两边上,在角两边所在直线上分别找两个点、,使三角形PMN的周长最小,这时分别作与关于直线对称,作与关于直线对称,连接、的直线与角两边所在直线的交点为所求。
典例剖析2-1
例2-1.如图,在四边形中,,,在,上分别找一个点M,N,使的周长最小,则___________°.
针对练习2-1
1..如图,分别是线段的垂直平分线,,一只小蚂蚁从点M出发爬到边上任意一点E,再爬到边上任意一点F,然后爬回M点,则小蚂蚁爬行的最短路径为( )
A. B. C. D.
2.如图,是内部的一条线段,在的两边,上各取一点C,D组成四边形,如何取点才能使该四边形周长最小?
3 .如图,点P是内任意一点,,点M和点N分别是射线和射线上的动点,,则周长的最小值是 .
2.类型四 定点在角内部,一动点在角的某边上,动点向另一边作垂线,求线段和最小值
求角内部一点与角一边所在直线上的一动点所连线段,加上这一点向角另一边所作垂线段之和最小的问题,只要找到角内部这个点关于动点所在直线的对称点,然后过对称点作角另一边的垂线与动点所在直线的交点,即为所求.
如图所示,点在的内,动点分别在的边上且交与点,这时作与关于直线对称,过点作交于点,则Q与的交点为所求。
典例剖析2-2
例2-2,在锐角三角形中,,, 的平分线交于点D,点M、N分别是和上的动点,则的最小值为( )
A. B. C.6 D.5
针对练习2-2
1.如图,在中,,,,是边上的中线,M是上的一个动点,N是上的一个动点,连接,,则的最小值是_________.
2.如图,在中,是的平分线.若分别是和上的动点,则的最小值是______________.
3.如图,已知钝角三角形的面积为20,最长边,平分,点分别是上的动点,则的最小值为 。
知识点3 两点两线型
1.类型五 两定点在角内部,两动点在角的两边上,求线段和最小值
求角内部两点与角两边所在直线上的两点所构成的四边形周长最小的问题,只要分别找到角内部这两个点关于角两边所在直线的对称点,连接对称点与角两边所在直线的交点,即为所求.
如图所示,点、点在的内,动点、动点分别在的两边上,在角两边所在直线上分别找两个点、,使四边形PQMN的周长最小,这时分别作与关于直线对称,作与关于直线对称,连接、的直线与角两边所在直线的交点为所求。
典例剖析3-1
例3-1.将军要检阅一队士兵,要求(如图所示);队伍长为a,沿河排开(从点P到点Q);将军从马棚M出发到达队头P,从P至Q检阅队伍后再赶到校场N.问:在什么位置列队(即选择点P和Q),可以使得将军走的总路程最短?
.
针对练习3-1
1.如图,是内部的一条线段,在的两边,上各取一点C,D组成四边形,如何取点才能使该四边形周长最小?
2.如图,已知两点P,Q在锐角内,分别在OA,OB上作点M,N,使最短.
3.如图,,M,N分别是OA,OB上的定点,P,Q分别是边OB,OA上的动点,如果记,,当最小时,则与的数量关系是______.
2.类型六 两定点在同一直线上同一侧或在两平行直线两侧,求线段和最小值
如图,直线和的同侧两点、,线段在直线上移动,使最小.
作法:将AC平移,使得点C和点D重合得到A'D,然后参照类型二作法即可。
(2)直线a与直线b平行, 、分别为直线a、直线b外侧的两点,在直线a、直线b上分别找M、N两点,且,使AM+MN+BN最小.
作法:将平移,使得点和点重合得到,连接交直线于点,作交直线于点,此时。
典例剖析3-2
例3-2 .如图,平行河岸两侧各有一城镇,,根据发展规划,要修建一条桥梁连接,两镇,已知相同长度造桥总价远大于陆上公路造价,为了尽量减少总造价,应该选择方案( )
A. B.
C. D.
针对练习3-2
1.如图所示,某条护城河在处直角转弯,河宽均为5 m,从A处到达B处,须经过两座桥(桥宽不计,桥与河垂直),设护城河以及两座桥都是东西、南北方向的,如何选址造桥可使从A处到B处的路程最短?请确定两座桥的位置.
2.如图所示,在一条河的两岸有两个村庄,现要在河上建一座小桥,桥的方向与河垂直,设河的宽度不变,试问:桥架在何处,才能使从A到B的距离最短?
3 .如图,是两个蓄水池,都在河流的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点(保留作图痕迹)
4.某大学建立分校,校本部与分校隔着两条平行的小河,如图所示,为校本部大门,为分校大门.为了方便人员来往,要在两条小河上各建一座桥,桥面垂直于河岸.为使两点间来往路段最短,试在图中画出符合条件的路径,并标明桥的位置.
知识点4.两点一线求线段差的最大值
类型七 两定点在同一直线上同一侧或在异侧,求线段差最大值
如图,直线同侧有两点、,在直线上求作一点,使最大.
作法:连接AB并延长交直线于点P,此时的最大值为线段AB的长
如图,直线异侧有两点、,在直线上求作一点,使最大.
作法:作点B关于直线的对称点B',连接AB'并延长交直线于点P,,此时的最大值为线段AB'的长。
典例剖析4
例4-1. 如图1、图2和图3,A、B两点在直线l同侧,且点A、B所在直线与l不平行,在直线l上画出符合要求的点P(不写做法与理由,保留作图痕迹).
(1)为最大值,在图1中的直线l上画出点的位置;
(2),在图2中的直线l上画出点的位置;
(3)为最小值,在图3中的直线l画出点的位置.
针对练习4
1.如图,已知两点在直线l的同一侧,根据题意,尺规作图.
(1)在图(1)直线l上找出一点P,使.
(2)在图(2)直线l上找出一点P,使的值最小.
(3)在图(3)直线l上找出一点P,使的值最大.
2.如图,点A,B在直线的同侧.
(1)试在直线上取一点M,使最小;
(2)试在直线上取一点N,使最大.
人教版八年级数学上名师点拨精练
轴对称
13.4 最短路径问题
学习目标
1.能利用轴对称解决简单的最短路径问题。体会图形的变化在解诀最值问题中的作用。
2.感悟转化思想。
重点:利用轴对称将最短路径问题转化为“两点之间,线段最短”问题。
难点:路径最短的证明。
老师告诉你
1.最短路径问题的类型
(1)两点一线型的线段和的最小值问题;(2)两线一点型的线段和的最小值问题;(3)两点两线型的线段和的最小值问题。
2.解决最短路径问题的方法
借助轴对称或平移的知识,化折为直,利用两点之间线段最短或垂线段最短来求线段和的最小值。
知识点拨
知识点1 两点一线型
1.类型一 两定点在直线两侧,动点在直线上,求线段和最小值
求直线异侧的两点与直线上一点所连线段的和最小的问题,只要连接这两点,与直线的交点即为所求.
如图所示,点A,B分别是直线l异侧的两个点,在l上找一个点C,使CA+CB最短,这时点C是直线l与AB的交点.
2.类型二 两定点在直线同侧,动点在直线上,求线段和最小值
求直线同侧的两点与直线上一点所连线段的和最小的问题,只要找到其中一个点关于这条直线的对称点,连接对称点与另一个点,则与该直线的交点即为所求.
如图所示,点A,B分别是直线l同侧的两个点,在l上找一个点C,使CA+CB最短,这时先作点B关于直线l的对称点B′,则点C是直线l与AB′的交点.
典例剖析1
例1-1 .如图,一辆汽车在笔直的公路AB上由A向B行驶, M,N分别是位于公路AB两侧的村庄,当汽车行驶到哪个位置时,与村庄M,N的距离相等?(用圆规和直尺作图,写出作法并保留作图痕迹)
答案:如图,①连接MN;
②作线段MN的垂直平分线l,交直线AB于点C,则点C即所求位置.
例1-2 .如图,在中,,,面积是10;的垂直平分线分别交,边于E、D两点,若点F为边的中点,点P为线段上一动点,则周长的最小值为( )
A.7 B.9 C.10 D.14
【答案】A
【分析】连接,根据线段垂直平分线性质得,周长,再根据等腰三角形的性质和三角形的面积求出,,即可得出答案.
【详解】解:如图所示.连接,
∵是的垂直平分线,
∴,
∴周长.
连接,
∵,点F是的中点,
∴,
∴.
∵,
∴,,
∴周长的最小值是.
故选:A.
【点睛】本题主要考查了等腰三角形的性质,线段垂直平分线的性质,根据轴对称求线段和最小值等,判断周长的最小值是解题的关键.
针对练习1
1.某市计划在公路l旁修建一个飞机场M,现有如下四种方案,则机场M到A、B两个城市之间的距离之和最短的方案是( )
A. B.
C. D.
答案:B
解析:作点A关于直线l的对称点,连接交直线l于M,
根据两点之间线段最短,可知机场M到A、B两个城市之间的距离之和最短.
故选:B.
2.如图,在正方形网格中有M,N两点,在直线l上求一点P,使最短,则点P应选在( )
A.A点 B.B点 C.C点 D.D点
答案:C
解析:如图,点是点M关于直线l的对称点,连接,则与直线l的交点,即为点P,此时最短,
与直线l交于点C,
点P应选C点.
故选C.
3.如图,点A,B在直线l同侧,在直线l上取一点P,使得最小,对点P的位置叙述正确的是( )
A.作线段的垂直平分线与直线l的交点,即为点P
B.过点A作直线l的垂线,垂足即为点P
C.作点B关于直线l的对称点,连接,与直线的交点,即为点P
D.延长与直线l的交点,即为点P
答案:C
解析:正确作法如下:如图,作点B关于直线l的对称点,连接,与直线l的交点,即为点P,
,
理由如下:在l上异于点P的位置任取一点H,连接,,,
,
B、关于直线l对称,
,
,
最短,
故选:C.
4.在一条沿直线铺设的电缆一侧有P,Q两个小区,要求在直线l上的某处选取一点M,向P,Q两个小区铺设电缆,现有如下四种铺设方案,图中实线表示铺设的电缆,则所需电缆材料最短的是( )
A. B.
C. D.
答案:D
解析:所需电缆材料最短,
作点P关于直线l的对称点,连接对称点与点Q,与直线l交于点M,连接,QM所得电缆材料最短,
故选:D.
知识点2 两线一点型
1.类型三 一定点在角内部,两动点在角的两边上,求线段和最小值
求角内部一点与角两边所在直线上的两点所构成的三角形周长最小的问题,只要分别找到角内部这个点关于角两边所在直线的对称点,连接对称点与角两边所在直线的交点,即为所求.
如图所示,点在的内,动点、动点分别在的两边上,在角两边所在直线上分别找两个点、,使三角形PMN的周长最小,这时分别作与关于直线对称,作与关于直线对称,连接、的直线与角两边所在直线的交点为所求。
典例剖析2-1
例2-1.如图,在四边形中,,,在,上分别找一个点M,N,使的周长最小,则___________°.
答案:150
解析:作A关于和的对称点,,连接,交于M,交于N,则即为的周长最小值.
,
,
,,且,,
故答案为:150.
针对练习2-1
1.如图,分别是线段的垂直平分线,,一只小蚂蚁从点M出发爬到边上任意一点E,再爬到边上任意一点F,然后爬回M点,则小蚂蚁爬行的最短路径为( )
A. B. C. D.
【答案】B
【分析】由题意可知与的交点为E,与的交点为F,根据垂直平分线的性质计算即可;
【详解】由题意可知与的交点为E,与的交点为F.
∵分别是线段的垂直平分线,
∴,
∴小蚂蚁爬行的最短路径为.
【点睛】本题主要考查了最短路线问题和垂直平分线的性质,准确计算是解题的关键.
2.如图,是内部的一条线段,在的两边,上各取一点C,D组成四边形,如何取点才能使该四边形周长最小?
答案:见解析
解析:(1)作出点A关于直线的对称点C;
(2)作出点B关于直线的对称点D;
(3)连接,交于点E,交于点F,
(4)连接,,
则四边形即为所求.
3 .如图,点P是内任意一点,,点M和点N分别是射线和射线上的动点,,则周长的最小值是 .
【答案】
【分析】分别作点P关于的对称点C、D,连接,分别交于点M、N,连接,当点M、N在上时,的周长最小.
解:分别作点P关于的对称点C、D,连接,分别交于点M、N,连接.
∵点P关于的对称点为C,关于的对称点为D,
∴;
∵点P关于的对称点为D,
∴,
∴,,
∴是等边三角形,
∴.
∴的周长的最小值.
故答案为:.
【点拨】本题主要考查最短路径问题和等边三角形的判定. 作点P关于OA、OB的对称点C、D是解题的关键所在.
2.类型四 定点在角内部,一动点在角的某边上,动点向另一边作垂线,求线段和最小值
求角内部一点与角一边所在直线上的一动点所连线段,加上这一点向角另一边所作垂线段之和最小的问题,只要找到角内部这个点关于动点所在直线的对称点,然后过对称点作角另一边的垂线与动点所在直线的交点,即为所求.
如图所示,点在的内,动点分别在的边上且交与点,这时作与关于直线对称,过点作交于点,则Q与的交点为所求。
典例剖析2-2
例2-2,在锐角三角形中,,, 的平分线交于点D,点M、N分别是和上的动点,则的最小值为( )
A. B. C.6 D.5
【答案】D
【分析】如下图,先根据三角形全等的判定定理与性质可得,再根据两点之间线段最短可得的最小值为,然后根据垂线段最短可得当时,取得最小值,最后利用三角形的面积公式即可得.
解:如图,在上取一点E,使,连接,
是的平分线,
,
在和中,
,
,
,
,
由两点之间线段最短得:当点共线时,取最小值,最小值为,
又由垂线段最短得:当时,取得最小值,
,
,
解得,
即的最小值为5,
故选D.
【点拨】本题考查了角平分线的定义、三角形全等的判定定理与性质、两点之间线段最短、垂线段最短等知识点,正确找出取得最小值时的位置是解题关键.
针对练习2-2
1.如图,在中,,,,是边上的中线,M是上的一个动点,N是上的一个动点,连接,,则的最小值是_________.
答案:或
解析:连接,,
,是中线,
,,,
是的垂直平分线,
,
,
即当点C、M、N三点共线时,最小值为的长,
时,最短,
,
,
最小值为:,
故答案为:.
.
2.如图,在中,是的平分线.若分别是和上的动点,则的最小值是______________.
答案:
解析:如图,过点作于点,交于点,则此时的值最小.是的平分线,垂直平分的最小值为的长.,,故的最小值是.
3.如图,已知钝角三角形的面积为20,最长边,平分,点分别是上的动点,则的最小值为 。
答案:4
解析:过点C作于点E,交于点M,过点M作于点N.
平分,于点E,于点N,,
,即就是的最小值.
三角形的面积为20,,,解得.
的最小值为4.
知识点3 两点两线型
1.类型五 两定点在角内部,两动点在角的两边上,求线段和最小值
求角内部两点与角两边所在直线上的两点所构成的四边形周长最小的问题,只要分别找到角内部这两个点关于角两边所在直线的对称点,连接对称点与角两边所在直线的交点,即为所求.
如图所示,点、点在的内,动点、动点分别在的两边上,在角两边所在直线上分别找两个点、,使四边形PQMN的周长最小,这时分别作与关于直线对称,作与关于直线对称,连接、的直线与角两边所在直线的交点为所求。
典例剖析3-1
例3-1.将军要检阅一队士兵,要求(如图所示);队伍长为a,沿河排开(从点P到点Q);将军从马棚M出发到达队头P,从P至Q检阅队伍后再赶到校场N.问:在什么位置列队(即选择点P和Q),可以使得将军走的总路程最短?
答案:见解析
解析:如图,作,使得,作点E关于的对称点F,连接交于点Q,在上截取,连接,线路时,的值最小.
.
针对练习3-1
1.如图,是内部的一条线段,在的两边,上各取一点C,D组成四边形,如何取点才能使该四边形周长最小?
答案:见解析
解析:(1)作出点A关于直线的对称点C;
(2)作出点B关于直线的对称点D;
(3)连接,交于点E,交于点F,
(4)连接,,
则四边形即为所求.
2.如图,已知两点P,Q在锐角内,分别在OA,OB上作点M,N,使最短.
答案:如图所示.
作点P关于OA的对称点,作点Q关于OB的对称点,连接,分别交OA,OB于点M,N,
则
3.如图,,M,N分别是OA,OB上的定点,P,Q分别是边OB,OA上的动点,如果记,,当最小时,则与的数量关系是______.
答案:
解析:如图,作M关于OB的对称点,N关于OA的对称点,连接交OA于Q,交OB于P,则最小,
易知,,
,,
,
.
,
故答案为:.
2.类型六 两定点在同一直线上同一侧或在两平行直线两侧,求线段和最小值
如图,直线和的同侧两点、,线段在直线上移动,使最小.
作法:将AC平移,使得点C和点D重合得到A'D,然后参照类型二作法即可。
(2)直线a与直线b平行, 、分别为直线a、直线b外侧的两点,在直线a、直线b上分别找M、N两点,且,使AM+MN+BN最小.
作法:将平移,使得点和点重合得到,连接交直线于点,作交直线于点,此时。
典例剖析3-2
例3-2 .如图,平行河岸两侧各有一城镇,,根据发展规划,要修建一条桥梁连接,两镇,已知相同长度造桥总价远大于陆上公路造价,为了尽量减少总造价,应该选择方案( )
A. B.
C. D.
【答案】C
【分析】作PP'垂直于河岸L,使PP′等于河宽,连接QP′,与河岸L相交于N,作NM⊥L,根据平行线的判定与性质,易证得此时PM+NQ最短.
【详解】解:如图,作PP'垂直于河岸L,使PP′等于河宽,连接QP′,与河岸L相交于N,作NM⊥L,则MN∥PP′且MN=PP′,于是四边形PMNP′为平行四边形,故PM=NP′.根据“两点之间线段最短”,QP′最短,即PM+NQ最短.观察选项,选项C符合题意.
故选C.
【点睛】本题主要考查最短路径问题,解此题的关键在于熟练掌握其知识点.
针对练习3-2
1.如图所示,某条护城河在处直角转弯,河宽均为5 m,从A处到达B处,须经过两座桥(桥宽不计,桥与河垂直),设护城河以及两座桥都是东西、南北方向的,如何选址造桥可使从A处到B处的路程最短?请确定两座桥的位置.
答案:见解析
解析:如图所示,作法如下:
(1)过点A作,使等于河宽;过点B作,使等于河宽(相当于将桥平移到,的位置).
(2)连接,分别与河岸,相交于点,.
(3)过点作于点D,过点作于点E,
由作图可知,
最短路径为,
,即为两座桥的位置.
2.如图所示,在一条河的两岸有两个村庄,现要在河上建一座小桥,桥的方向与河垂直,设河的宽度不变,试问:桥架在何处,才能使从A到B的距离最短?
答案:如图,作垂直于河岸GH,且等于河宽,
连接,与河岸EF相交于P,作,交GH于点D,
则且.
连接BD,利用平移可知.
根据“两点之间,线段最短”,知最短,可知满足题意的从A到B的路径中,路径最短.
故桥架在PD处符合题意.
:
3 .如图,是两个蓄水池,都在河流的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点(保留作图痕迹)
答案:
4.某大学建立分校,校本部与分校隔着两条平行的小河,如图所示,为校本部大门,为分校大门.为了方便人员来往,要在两条小河上各建一座桥,桥面垂直于河岸.为使两点间来往路段最短,试在图中画出符合条件的路径,并标明桥的位置.
答案:设在小河甲上建桥,小河乙上建桥,则两点间来往路径是折线.过点作河岸,过点作河岸,方向是对着小河,使小河甲的宽度,小河乙的宽度,连接,则折线的长度=折线的长度=折线的长度+两河的宽度和,为使来往路段最短,需使折线的长度最小,因此连接交于点,交于点,搭桥,则线段的长度即折线的长度的最小值.因此,符合条件的路径为折线,小河甲和小河乙上桥的位置分别是.
知识点4.两点一线求线段差的最大值
类型七 两定点在同一直线上同一侧或在异侧,求线段差最大值
如图,直线同侧有两点、,在直线上求作一点,使最大.
作法:连接AB并延长交直线于点P,此时的最大值为线段AB的长
如图,直线异侧有两点、,在直线上求作一点,使最大.
作法:作点B关于直线的对称点B',连接AB'并延长交直线于点P,,此时的最大值为线段AB'的长。
典例剖析4
例4-1. 如图1、图2和图3,A、B两点在直线l同侧,且点A、B所在直线与l不平行,在直线l上画出符合要求的点P(不写做法与理由,保留作图痕迹).
(1)为最大值,在图1中的直线l上画出点的位置;
(2),在图2中的直线l上画出点的位置;
(3)为最小值,在图3中的直线l画出点的位置.
(1)的位置见解析;(2)的位置见解析;(3)的位置见解析.
【分析】(1)根据三角形两边之差小于第三边可得,且当P在AB的延长线上时等号成立,由此可得点的位置;
(2)根据垂直平分线上的点到线段两端距离相等,作AB的垂直平分线与l的交点即为点的位置;
(3)作B点关于直线l的对称点,连接与l的交点即为点的位置,原理是两点之间线段最短和轴对称的性质.
【详解】解:(1)如图,点的位置如下;
(2)如图,点的位置如下;
(3)如图,点的位置如下.
【点拨】本题考查作线段的垂直平分线,涉及的知识点有三角形三边关系、垂直平分线的性质和轴对称——最短路径问题.掌握相关定理,能正确分析是解题关键.
针对练习4
1.如图,已知两点在直线l的同一侧,根据题意,尺规作图.
(1)在图(1)直线l上找出一点P,使.
(2)在图(2)直线l上找出一点P,使的值最小.
(3)在图(3)直线l上找出一点P,使的值最大.
答案:
(1)如图所示:
此时
(2).如图所示:
此时最小
(3).如图所示:
此时最大.
2.如图,点A,B在直线的同侧.
(1)试在直线上取一点M,使最小;
(2)试在直线上取一点N,使最大.
答案:(1)如图,作点A关于直线的对称点C,连接BC交直线于点M连接MA,此时,由两点之间线段最短知,此时最小,故点M即所求.
(2)如图,连接BA并延长,交直线于点N,此时,由三角形的三边关系知,此时最大,故点N即所求.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版八年级数学上名师点拨精练
轴对称
13.4 最短路径问题
学习目标
1.能利用轴对称解决简单的最短路径问题。体会图形的变化在解诀最值问题中的作用。
2.感悟转化思想。
重点:利用轴对称将最短路径问题转化为“两点之间,线段最短”问题。
难点:路径最短的证明。
老师告诉你
1.最短路径问题的类型
(1)两点一线型的线段和的最小值问题;(2)两线一点型的线段和的最小值问题;(3)两点两线型的线段和的最小值问题。
2.解决最短路径问题的方法
借助轴对称或平移的知识,化折为直,利用两点之间线段最短或垂线段最短来求线段和的最小值。
知识点拨
知识点1 两点一线型
1.类型一 两定点在直线两侧,动点在直线上,求线段和最小值
求直线异侧的两点与直线上一点所连线段的和最小的问题,只要连接这两点,与直线的交点即为所求.
如图所示,点A,B分别是直线l异侧的两个点,在l上找一个点C,使CA+CB最短,这时点C是直线l与AB的交点.
2.类型二 两定点在直线同侧,动点在直线上,求线段和最小值
求直线同侧的两点与直线上一点所连线段的和最小的问题,只要找到其中一个点关于这条直线的对称点,连接对称点与另一个点,则与该直线的交点即为所求.
如图所示,点A,B分别是直线l同侧的两个点,在l上找一个点C,使CA+CB最短,这时先作点B关于直线l的对称点B′,则点C是直线l与AB′的交点.
典例剖析1
例1-1 .如图,一辆汽车在笔直的公路AB上由A向B行驶, M,N分别是位于公路AB两侧的村庄,当汽车行驶到哪个位置时,与村庄M,N的距离相等?(用圆规和直尺作图,写出作法并保留作图痕迹)
例1-2 .如图,在中,,,面积是10;的垂直平分线分别交,边于E、D两点,若点F为边的中点,点P为线段上一动点,则周长的最小值为( )
A.7 B.9 C.10 D.14
针对练习1
1.某市计划在公路l旁修建一个飞机场M,现有如下四种方案,则机场M到A、B两个城市之间的距离之和最短的方案是( )
A. B.
C. D.
2.如图,在正方形网格中有M,N两点,在直线l上求一点P,使最短,则点P应选在( )
A.A点 B.B点 C.C点 D.D点
3.如图,点A,B在直线l同侧,在直线l上取一点P,使得最小,对点P的位置叙述正确的是( )
A.作线段的垂直平分线与直线l的交点,即为点P
B.过点A作直线l的垂线,垂足即为点P
C.作点B关于直线l的对称点,连接,与直线的交点,即为点P
D.延长与直线l的交点,即为点P
4.在一条沿直线铺设的电缆一侧有P,Q两个小区,要求在直线l上的某处选取一点M,向P,Q两个小区铺设电缆,现有如下四种铺设方案,图中实线表示铺设的电缆,则所需电缆材料最短的是( )
A. B.
C. D.
知识点2 两线一点型
1.类型三 一定点在角内部,两动点在角的两边上,求线段和最小值
求角内部一点与角两边所在直线上的两点所构成的三角形周长最小的问题,只要分别找到角内部这个点关于角两边所在直线的对称点,连接对称点与角两边所在直线的交点,即为所求.
如图所示,点在的内,动点、动点分别在的两边上,在角两边所在直线上分别找两个点、,使三角形PMN的周长最小,这时分别作与关于直线对称,作与关于直线对称,连接、的直线与角两边所在直线的交点为所求。
典例剖析2-1
例2-1.如图,在四边形中,,,在,上分别找一个点M,N,使的周长最小,则___________°.
针对练习2-1
1..如图,分别是线段的垂直平分线,,一只小蚂蚁从点M出发爬到边上任意一点E,再爬到边上任意一点F,然后爬回M点,则小蚂蚁爬行的最短路径为( )
A. B. C. D.
2.如图,是内部的一条线段,在的两边,上各取一点C,D组成四边形,如何取点才能使该四边形周长最小?
3 .如图,点P是内任意一点,,点M和点N分别是射线和射线上的动点,,则周长的最小值是 .
2.类型四 定点在角内部,一动点在角的某边上,动点向另一边作垂线,求线段和最小值
求角内部一点与角一边所在直线上的一动点所连线段,加上这一点向角另一边所作垂线段之和最小的问题,只要找到角内部这个点关于动点所在直线的对称点,然后过对称点作角另一边的垂线与动点所在直线的交点,即为所求.
如图所示,点在的内,动点分别在的边上且交与点,这时作与关于直线对称,过点作交于点,则Q与的交点为所求。
典例剖析2-2
例2-2,在锐角三角形中,,, 的平分线交于点D,点M、N分别是和上的动点,则的最小值为( )
A. B. C.6 D.5
针对练习2-2
1.如图,在中,,,,是边上的中线,M是上的一个动点,N是上的一个动点,连接,,则的最小值是_________.
2.如图,在中,是的平分线.若分别是和上的动点,则的最小值是______________.
3.如图,已知钝角三角形的面积为20,最长边,平分,点分别是上的动点,则的最小值为 。
知识点3 两点两线型
1.类型五 两定点在角内部,两动点在角的两边上,求线段和最小值
求角内部两点与角两边所在直线上的两点所构成的四边形周长最小的问题,只要分别找到角内部这两个点关于角两边所在直线的对称点,连接对称点与角两边所在直线的交点,即为所求.
如图所示,点、点在的内,动点、动点分别在的两边上,在角两边所在直线上分别找两个点、,使四边形PQMN的周长最小,这时分别作与关于直线对称,作与关于直线对称,连接、的直线与角两边所在直线的交点为所求。
典例剖析3-1
例3-1.将军要检阅一队士兵,要求(如图所示);队伍长为a,沿河排开(从点P到点Q);将军从马棚M出发到达队头P,从P至Q检阅队伍后再赶到校场N.问:在什么位置列队(即选择点P和Q),可以使得将军走的总路程最短?
.
针对练习3-1
1.如图,是内部的一条线段,在的两边,上各取一点C,D组成四边形,如何取点才能使该四边形周长最小?
2.如图,已知两点P,Q在锐角内,分别在OA,OB上作点M,N,使最短.
3.如图,,M,N分别是OA,OB上的定点,P,Q分别是边OB,OA上的动点,如果记,,当最小时,则与的数量关系是______.
2.类型六 两定点在同一直线上同一侧或在两平行直线两侧,求线段和最小值
如图,直线和的同侧两点、,线段在直线上移动,使最小.
作法:将AC平移,使得点C和点D重合得到A'D,然后参照类型二作法即可。
(2)直线a与直线b平行, 、分别为直线a、直线b外侧的两点,在直线a、直线b上分别找M、N两点,且,使AM+MN+BN最小.
作法:将平移,使得点和点重合得到,连接交直线于点,作交直线于点,此时。
典例剖析3-2
例3-2 .如图,平行河岸两侧各有一城镇,,根据发展规划,要修建一条桥梁连接,两镇,已知相同长度造桥总价远大于陆上公路造价,为了尽量减少总造价,应该选择方案( )
A. B.
C. D.
针对练习3-2
1.如图所示,某条护城河在处直角转弯,河宽均为5 m,从A处到达B处,须经过两座桥(桥宽不计,桥与河垂直),设护城河以及两座桥都是东西、南北方向的,如何选址造桥可使从A处到B处的路程最短?请确定两座桥的位置.
2.如图所示,在一条河的两岸有两个村庄,现要在河上建一座小桥,桥的方向与河垂直,设河的宽度不变,试问:桥架在何处,才能使从A到B的距离最短?
3 .如图,是两个蓄水池,都在河流的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点(保留作图痕迹)
4.某大学建立分校,校本部与分校隔着两条平行的小河,如图所示,为校本部大门,为分校大门.为了方便人员来往,要在两条小河上各建一座桥,桥面垂直于河岸.为使两点间来往路段最短,试在图中画出符合条件的路径,并标明桥的位置.
知识点4.两点一线求线段差的最大值
类型七 两定点在同一直线上同一侧或在异侧,求线段差最大值
如图,直线同侧有两点、,在直线上求作一点,使最大.
作法:连接AB并延长交直线于点P,此时的最大值为线段AB的长
如图,直线异侧有两点、,在直线上求作一点,使最大.
作法:作点B关于直线的对称点B',连接AB'并延长交直线于点P,,此时的最大值为线段AB'的长。
典例剖析4
例4-1. 如图1、图2和图3,A、B两点在直线l同侧,且点A、B所在直线与l不平行,在直线l上画出符合要求的点P(不写做法与理由,保留作图痕迹).
(1)为最大值,在图1中的直线l上画出点的位置;
(2),在图2中的直线l上画出点的位置;
(3)为最小值,在图3中的直线l画出点的位置.
针对练习4
1.如图,已知两点在直线l的同一侧,根据题意,尺规作图.
(1)在图(1)直线l上找出一点P,使.
(2)在图(2)直线l上找出一点P,使的值最小.
(3)在图(3)直线l上找出一点P,使的值最大.
2.如图,点A,B在直线的同侧.
(1)试在直线上取一点M,使最小;
(2)试在直线上取一点N,使最大.
人教版八年级数学上名师点拨精练
轴对称
13.4 最短路径问题
学习目标
1.能利用轴对称解决简单的最短路径问题。体会图形的变化在解诀最值问题中的作用。
2.感悟转化思想。
重点:利用轴对称将最短路径问题转化为“两点之间,线段最短”问题。
难点:路径最短的证明。
老师告诉你
1.最短路径问题的类型
(1)两点一线型的线段和的最小值问题;(2)两线一点型的线段和的最小值问题;(3)两点两线型的线段和的最小值问题。
2.解决最短路径问题的方法
借助轴对称或平移的知识,化折为直,利用两点之间线段最短或垂线段最短来求线段和的最小值。
知识点拨
知识点1 两点一线型
1.类型一 两定点在直线两侧,动点在直线上,求线段和最小值
求直线异侧的两点与直线上一点所连线段的和最小的问题,只要连接这两点,与直线的交点即为所求.
如图所示,点A,B分别是直线l异侧的两个点,在l上找一个点C,使CA+CB最短,这时点C是直线l与AB的交点.
2.类型二 两定点在直线同侧,动点在直线上,求线段和最小值
求直线同侧的两点与直线上一点所连线段的和最小的问题,只要找到其中一个点关于这条直线的对称点,连接对称点与另一个点,则与该直线的交点即为所求.
如图所示,点A,B分别是直线l同侧的两个点,在l上找一个点C,使CA+CB最短,这时先作点B关于直线l的对称点B′,则点C是直线l与AB′的交点.
典例剖析1
例1-1 .如图,一辆汽车在笔直的公路AB上由A向B行驶, M,N分别是位于公路AB两侧的村庄,当汽车行驶到哪个位置时,与村庄M,N的距离相等?(用圆规和直尺作图,写出作法并保留作图痕迹)
答案:如图,①连接MN;
②作线段MN的垂直平分线l,交直线AB于点C,则点C即所求位置.
例1-2 .如图,在中,,,面积是10;的垂直平分线分别交,边于E、D两点,若点F为边的中点,点P为线段上一动点,则周长的最小值为( )
A.7 B.9 C.10 D.14
【答案】A
【分析】连接,根据线段垂直平分线性质得,周长,再根据等腰三角形的性质和三角形的面积求出,,即可得出答案.
【详解】解:如图所示.连接,
∵是的垂直平分线,
∴,
∴周长.
连接,
∵,点F是的中点,
∴,
∴.
∵,
∴,,
∴周长的最小值是.
故选:A.
【点睛】本题主要考查了等腰三角形的性质,线段垂直平分线的性质,根据轴对称求线段和最小值等,判断周长的最小值是解题的关键.
针对练习1
1.某市计划在公路l旁修建一个飞机场M,现有如下四种方案,则机场M到A、B两个城市之间的距离之和最短的方案是( )
A. B.
C. D.
答案:B
解析:作点A关于直线l的对称点,连接交直线l于M,
根据两点之间线段最短,可知机场M到A、B两个城市之间的距离之和最短.
故选:B.
2.如图,在正方形网格中有M,N两点,在直线l上求一点P,使最短,则点P应选在( )
A.A点 B.B点 C.C点 D.D点
答案:C
解析:如图,点是点M关于直线l的对称点,连接,则与直线l的交点,即为点P,此时最短,
与直线l交于点C,
点P应选C点.
故选C.
3.如图,点A,B在直线l同侧,在直线l上取一点P,使得最小,对点P的位置叙述正确的是( )
A.作线段的垂直平分线与直线l的交点,即为点P
B.过点A作直线l的垂线,垂足即为点P
C.作点B关于直线l的对称点,连接,与直线的交点,即为点P
D.延长与直线l的交点,即为点P
答案:C
解析:正确作法如下:如图,作点B关于直线l的对称点,连接,与直线l的交点,即为点P,
,
理由如下:在l上异于点P的位置任取一点H,连接,,,
,
B、关于直线l对称,
,
,
最短,
故选:C.
4.在一条沿直线铺设的电缆一侧有P,Q两个小区,要求在直线l上的某处选取一点M,向P,Q两个小区铺设电缆,现有如下四种铺设方案,图中实线表示铺设的电缆,则所需电缆材料最短的是( )
A. B.
C. D.
答案:D
解析:所需电缆材料最短,
作点P关于直线l的对称点,连接对称点与点Q,与直线l交于点M,连接,QM所得电缆材料最短,
故选:D.
知识点2 两线一点型
1.类型三 一定点在角内部,两动点在角的两边上,求线段和最小值
求角内部一点与角两边所在直线上的两点所构成的三角形周长最小的问题,只要分别找到角内部这个点关于角两边所在直线的对称点,连接对称点与角两边所在直线的交点,即为所求.
如图所示,点在的内,动点、动点分别在的两边上,在角两边所在直线上分别找两个点、,使三角形PMN的周长最小,这时分别作与关于直线对称,作与关于直线对称,连接、的直线与角两边所在直线的交点为所求。
典例剖析2-1
例2-1.如图,在四边形中,,,在,上分别找一个点M,N,使的周长最小,则___________°.
答案:150
解析:作A关于和的对称点,,连接,交于M,交于N,则即为的周长最小值.
,
,
,,且,,
故答案为:150.
针对练习2-1
1.如图,分别是线段的垂直平分线,,一只小蚂蚁从点M出发爬到边上任意一点E,再爬到边上任意一点F,然后爬回M点,则小蚂蚁爬行的最短路径为( )
A. B. C. D.
【答案】B
【分析】由题意可知与的交点为E,与的交点为F,根据垂直平分线的性质计算即可;
【详解】由题意可知与的交点为E,与的交点为F.
∵分别是线段的垂直平分线,
∴,
∴小蚂蚁爬行的最短路径为.
【点睛】本题主要考查了最短路线问题和垂直平分线的性质,准确计算是解题的关键.
2.如图,是内部的一条线段,在的两边,上各取一点C,D组成四边形,如何取点才能使该四边形周长最小?
答案:见解析
解析:(1)作出点A关于直线的对称点C;
(2)作出点B关于直线的对称点D;
(3)连接,交于点E,交于点F,
(4)连接,,
则四边形即为所求.
3 .如图,点P是内任意一点,,点M和点N分别是射线和射线上的动点,,则周长的最小值是 .
【答案】
【分析】分别作点P关于的对称点C、D,连接,分别交于点M、N,连接,当点M、N在上时,的周长最小.
解:分别作点P关于的对称点C、D,连接,分别交于点M、N,连接.
∵点P关于的对称点为C,关于的对称点为D,
∴;
∵点P关于的对称点为D,
∴,
∴,,
∴是等边三角形,
∴.
∴的周长的最小值.
故答案为:.
【点拨】本题主要考查最短路径问题和等边三角形的判定. 作点P关于OA、OB的对称点C、D是解题的关键所在.
2.类型四 定点在角内部,一动点在角的某边上,动点向另一边作垂线,求线段和最小值
求角内部一点与角一边所在直线上的一动点所连线段,加上这一点向角另一边所作垂线段之和最小的问题,只要找到角内部这个点关于动点所在直线的对称点,然后过对称点作角另一边的垂线与动点所在直线的交点,即为所求.
如图所示,点在的内,动点分别在的边上且交与点,这时作与关于直线对称,过点作交于点,则Q与的交点为所求。
典例剖析2-2
例2-2,在锐角三角形中,,, 的平分线交于点D,点M、N分别是和上的动点,则的最小值为( )
A. B. C.6 D.5
【答案】D
【分析】如下图,先根据三角形全等的判定定理与性质可得,再根据两点之间线段最短可得的最小值为,然后根据垂线段最短可得当时,取得最小值,最后利用三角形的面积公式即可得.
解:如图,在上取一点E,使,连接,
是的平分线,
,
在和中,
,
,
,
,
由两点之间线段最短得:当点共线时,取最小值,最小值为,
又由垂线段最短得:当时,取得最小值,
,
,
解得,
即的最小值为5,
故选D.
【点拨】本题考查了角平分线的定义、三角形全等的判定定理与性质、两点之间线段最短、垂线段最短等知识点,正确找出取得最小值时的位置是解题关键.
针对练习2-2
1.如图,在中,,,,是边上的中线,M是上的一个动点,N是上的一个动点,连接,,则的最小值是_________.
答案:或
解析:连接,,
,是中线,
,,,
是的垂直平分线,
,
,
即当点C、M、N三点共线时,最小值为的长,
时,最短,
,
,
最小值为:,
故答案为:.
.
2.如图,在中,是的平分线.若分别是和上的动点,则的最小值是______________.
答案:
解析:如图,过点作于点,交于点,则此时的值最小.是的平分线,垂直平分的最小值为的长.,,故的最小值是.
3.如图,已知钝角三角形的面积为20,最长边,平分,点分别是上的动点,则的最小值为 。
答案:4
解析:过点C作于点E,交于点M,过点M作于点N.
平分,于点E,于点N,,
,即就是的最小值.
三角形的面积为20,,,解得.
的最小值为4.
知识点3 两点两线型
1.类型五 两定点在角内部,两动点在角的两边上,求线段和最小值
求角内部两点与角两边所在直线上的两点所构成的四边形周长最小的问题,只要分别找到角内部这两个点关于角两边所在直线的对称点,连接对称点与角两边所在直线的交点,即为所求.
如图所示,点、点在的内,动点、动点分别在的两边上,在角两边所在直线上分别找两个点、,使四边形PQMN的周长最小,这时分别作与关于直线对称,作与关于直线对称,连接、的直线与角两边所在直线的交点为所求。
典例剖析3-1
例3-1.将军要检阅一队士兵,要求(如图所示);队伍长为a,沿河排开(从点P到点Q);将军从马棚M出发到达队头P,从P至Q检阅队伍后再赶到校场N.问:在什么位置列队(即选择点P和Q),可以使得将军走的总路程最短?
答案:见解析
解析:如图,作,使得,作点E关于的对称点F,连接交于点Q,在上截取,连接,线路时,的值最小.
.
针对练习3-1
1.如图,是内部的一条线段,在的两边,上各取一点C,D组成四边形,如何取点才能使该四边形周长最小?
答案:见解析
解析:(1)作出点A关于直线的对称点C;
(2)作出点B关于直线的对称点D;
(3)连接,交于点E,交于点F,
(4)连接,,
则四边形即为所求.
2.如图,已知两点P,Q在锐角内,分别在OA,OB上作点M,N,使最短.
答案:如图所示.
作点P关于OA的对称点,作点Q关于OB的对称点,连接,分别交OA,OB于点M,N,
则
3.如图,,M,N分别是OA,OB上的定点,P,Q分别是边OB,OA上的动点,如果记,,当最小时,则与的数量关系是______.
答案:
解析:如图,作M关于OB的对称点,N关于OA的对称点,连接交OA于Q,交OB于P,则最小,
易知,,
,,
,
.
,
故答案为:.
2.类型六 两定点在同一直线上同一侧或在两平行直线两侧,求线段和最小值
如图,直线和的同侧两点、,线段在直线上移动,使最小.
作法:将AC平移,使得点C和点D重合得到A'D,然后参照类型二作法即可。
(2)直线a与直线b平行, 、分别为直线a、直线b外侧的两点,在直线a、直线b上分别找M、N两点,且,使AM+MN+BN最小.
作法:将平移,使得点和点重合得到,连接交直线于点,作交直线于点,此时。
典例剖析3-2
例3-2 .如图,平行河岸两侧各有一城镇,,根据发展规划,要修建一条桥梁连接,两镇,已知相同长度造桥总价远大于陆上公路造价,为了尽量减少总造价,应该选择方案( )
A. B.
C. D.
【答案】C
【分析】作PP'垂直于河岸L,使PP′等于河宽,连接QP′,与河岸L相交于N,作NM⊥L,根据平行线的判定与性质,易证得此时PM+NQ最短.
【详解】解:如图,作PP'垂直于河岸L,使PP′等于河宽,连接QP′,与河岸L相交于N,作NM⊥L,则MN∥PP′且MN=PP′,于是四边形PMNP′为平行四边形,故PM=NP′.根据“两点之间线段最短”,QP′最短,即PM+NQ最短.观察选项,选项C符合题意.
故选C.
【点睛】本题主要考查最短路径问题,解此题的关键在于熟练掌握其知识点.
针对练习3-2
1.如图所示,某条护城河在处直角转弯,河宽均为5 m,从A处到达B处,须经过两座桥(桥宽不计,桥与河垂直),设护城河以及两座桥都是东西、南北方向的,如何选址造桥可使从A处到B处的路程最短?请确定两座桥的位置.
答案:见解析
解析:如图所示,作法如下:
(1)过点A作,使等于河宽;过点B作,使等于河宽(相当于将桥平移到,的位置).
(2)连接,分别与河岸,相交于点,.
(3)过点作于点D,过点作于点E,
由作图可知,
最短路径为,
,即为两座桥的位置.
2.如图所示,在一条河的两岸有两个村庄,现要在河上建一座小桥,桥的方向与河垂直,设河的宽度不变,试问:桥架在何处,才能使从A到B的距离最短?
答案:如图,作垂直于河岸GH,且等于河宽,
连接,与河岸EF相交于P,作,交GH于点D,
则且.
连接BD,利用平移可知.
根据“两点之间,线段最短”,知最短,可知满足题意的从A到B的路径中,路径最短.
故桥架在PD处符合题意.
:
3 .如图,是两个蓄水池,都在河流的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点(保留作图痕迹)
答案:
4.某大学建立分校,校本部与分校隔着两条平行的小河,如图所示,为校本部大门,为分校大门.为了方便人员来往,要在两条小河上各建一座桥,桥面垂直于河岸.为使两点间来往路段最短,试在图中画出符合条件的路径,并标明桥的位置.
答案:设在小河甲上建桥,小河乙上建桥,则两点间来往路径是折线.过点作河岸,过点作河岸,方向是对着小河,使小河甲的宽度,小河乙的宽度,连接,则折线的长度=折线的长度=折线的长度+两河的宽度和,为使来往路段最短,需使折线的长度最小,因此连接交于点,交于点,搭桥,则线段的长度即折线的长度的最小值.因此,符合条件的路径为折线,小河甲和小河乙上桥的位置分别是.
知识点4.两点一线求线段差的最大值
类型七 两定点在同一直线上同一侧或在异侧,求线段差最大值
如图,直线同侧有两点、,在直线上求作一点,使最大.
作法:连接AB并延长交直线于点P,此时的最大值为线段AB的长
如图,直线异侧有两点、,在直线上求作一点,使最大.
作法:作点B关于直线的对称点B',连接AB'并延长交直线于点P,,此时的最大值为线段AB'的长。
典例剖析4
例4-1. 如图1、图2和图3,A、B两点在直线l同侧,且点A、B所在直线与l不平行,在直线l上画出符合要求的点P(不写做法与理由,保留作图痕迹).
(1)为最大值,在图1中的直线l上画出点的位置;
(2),在图2中的直线l上画出点的位置;
(3)为最小值,在图3中的直线l画出点的位置.
(1)的位置见解析;(2)的位置见解析;(3)的位置见解析.
【分析】(1)根据三角形两边之差小于第三边可得,且当P在AB的延长线上时等号成立,由此可得点的位置;
(2)根据垂直平分线上的点到线段两端距离相等,作AB的垂直平分线与l的交点即为点的位置;
(3)作B点关于直线l的对称点,连接与l的交点即为点的位置,原理是两点之间线段最短和轴对称的性质.
【详解】解:(1)如图,点的位置如下;
(2)如图,点的位置如下;
(3)如图,点的位置如下.
【点拨】本题考查作线段的垂直平分线,涉及的知识点有三角形三边关系、垂直平分线的性质和轴对称——最短路径问题.掌握相关定理,能正确分析是解题关键.
针对练习4
1.如图,已知两点在直线l的同一侧,根据题意,尺规作图.
(1)在图(1)直线l上找出一点P,使.
(2)在图(2)直线l上找出一点P,使的值最小.
(3)在图(3)直线l上找出一点P,使的值最大.
答案:
(1)如图所示:
此时
(2).如图所示:
此时最小
(3).如图所示:
此时最大.
2.如图,点A,B在直线的同侧.
(1)试在直线上取一点M,使最小;
(2)试在直线上取一点N,使最大.
答案:(1)如图,作点A关于直线的对称点C,连接BC交直线于点M连接MA,此时,由两点之间线段最短知,此时最小,故点M即所求.
(2)如图,连接BA并延长,交直线于点N,此时,由三角形的三边关系知,此时最大,故点N即所求.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
