2024-2025学年四川省成都市天府师大一中高级中学高二(上)月考数学试卷(9月份)(含答案)
文档属性
| 名称 | 2024-2025学年四川省成都市天府师大一中高级中学高二(上)月考数学试卷(9月份)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 178.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-17 00:00:00 | ||
图片预览



文档简介
2024-2025学年四川省成都市天府师大一中高级中学高二(上)月考
数学试卷(9月份)
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.要调查下列问题,适合采用全面调查普查的是( )
A. 某城市居民月份人均网上购物的次数 B. 某品牌新能源汽车最大续航里程
C. 检测一批灯泡的使用寿命 D. 调查一个班级学生每周的体育锻炼时间
2.成飞中学高一年级人,高二年级人,现按比例分层随机抽样的方法从高一、高二年级抽取名同学朗诵“成飞赋”,则高二抽取的人数为( )
A. B. C. D.
3.下列说法一定正确的是 .
A. 一名篮球运动员,号称“百发百中”,若罚球三次,不会出现三投都不中的情况
B. 一个骰子掷一次得到的概率是,则掷次一定会出现一次
C. 若买彩票中奖的概率为万分之一,则买一万元的彩票一定会中奖一元
D. 随机事件发生的概率与试验次数无关
4.甲乙两人在相同条件下各打靶次,每次打靶的成绩情况如图所示:下列说法错误的是( )
A. 从平均数和方差相结合看,甲波动比较大,乙相对比较稳定
B. 从折线统计图上两人射击命中环数走势看,甲更有潜力
C. 从平均数和命中环及环以上的次数相结合看,甲成绩较好
D. 从平均数和中位数相结合看,乙成绩较好
5.续航能力关乎无人机的“生命力”,太阳能供能是实现无人机长时续航的重要路径之一.某大学科研团队利用自主开发的新型静电电机,成功研制出仅重克的太阳能动力微型无人机,实现纯自然光供能下的持续飞行.为激发同学们对无人机的兴趣,某校无人机兴趣社团在校内进行选拔赛,名参赛学生的成绩依次为,,,,,,,,则这组数据的上四分位数也叫第百分位数为( )
A. B. C. D.
6.【选考北师大版】小明在整理数据时得到了该组数据的平均数为,方差为,后来发现有两个数据记录有误,一个错将记录为,另一个错将记录为在对错误的数据进行更正后,重新求得该组数据的平均数为,方差为,则( )
A. , B. ,
C. , D. ,
7.在一个不透明的袋子里装有四个小球,球上分别标有,,,四个数字,这些小球除数字外都相同甲、乙两人玩“猜数字”游戏,甲先从袋中任意摸出一个小球,将小球上的数字记为,再由乙猜这个小球上的数字,记为如果,满足,那么就称甲、乙两人“心领神会”,则两人“心领神会”的概率是( )
A. B. C. D.
8.已知事件,,且,,则下列说法正确的是( )
A. 若,则,
B. 若与互斥,则,
C. 若与相互独立,则,
D. 若与相互独立,则,
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.甲、乙两人进行篮球比赛,若甲投中的概率为,乙投不中的概率为,且两人投篮互不影响,若两人各投篮一次,则下列结论中正确的是( )
A. 两人都投中的概率为 B. 至少一人投中的概率为
C. 至多一人投中的概率为 D. 恰好有一人投中的概率为
10.有两组样本数据,分别为,,,和,,,,且平均数,方差分别为和,将两组数据合并为,,,,重新计算平均数和方差,则( )
A. 平均数为 B. 平均数为 C. 方差为 D. 方差为
11.某保险公司为客户定制了个险种:甲,一年期短期;乙,两全保险;丙,理财类保险;丁,定期寿险;戊,重大疾病保险.各种保险按相关约定进行参保与理赔.该保险公司对个险种参保客户进行抽样调查,得到如图所示的统计图表.则( )
A. 丁险种参保人数超过五成 B. 岁以上参保人数超过总参保人数的五成
C. 周岁人群参保的总费用最少 D. 人均参保费用不超过元
三、填空题:本题共3小题,每小题5分,共15分。
12.已知某运动员每次投篮命中的概率都为,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算机产生到之间取整数值的随机数,指定,,,表示命中,,,,,,表示不命中;再以三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下组随机数:
据此估计,该运动员三次投篮恰有两次命中的概率为 .
13.若样本数据,,,的方差为,则数据,,,的方差为______.
14.若三个元件,,按照如图的方式连接成一个系统,每个元件是否正常工作不受其他元件的影响,当元件正常工作且,中至少有一个正常工作时,系统就正常工作,若元件,正常工作的概率依次为,,且这个系统正常工作的概率为,则元件正常工作的概率为______.
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
从,,,这四个数字中,不放回地取两次,每次取一个,构成数对,为第一次取到的数字,为第二次取到的数字设事件“第一次取出的数字是“,“第二次取出的数字是”.
写出此试验的样本空间及,的值;
判断与是不是互斥事件,并求的值.
16.本小题分
甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取次,记录如下:
甲
乙
求甲成绩的分位数;
现要从中选派一人参加数学竞赛,从统计学的角度在平均数、方差或标准差中选两个考虑,你认为选派哪位学生参加合适?请说明理由?
17.本小题分
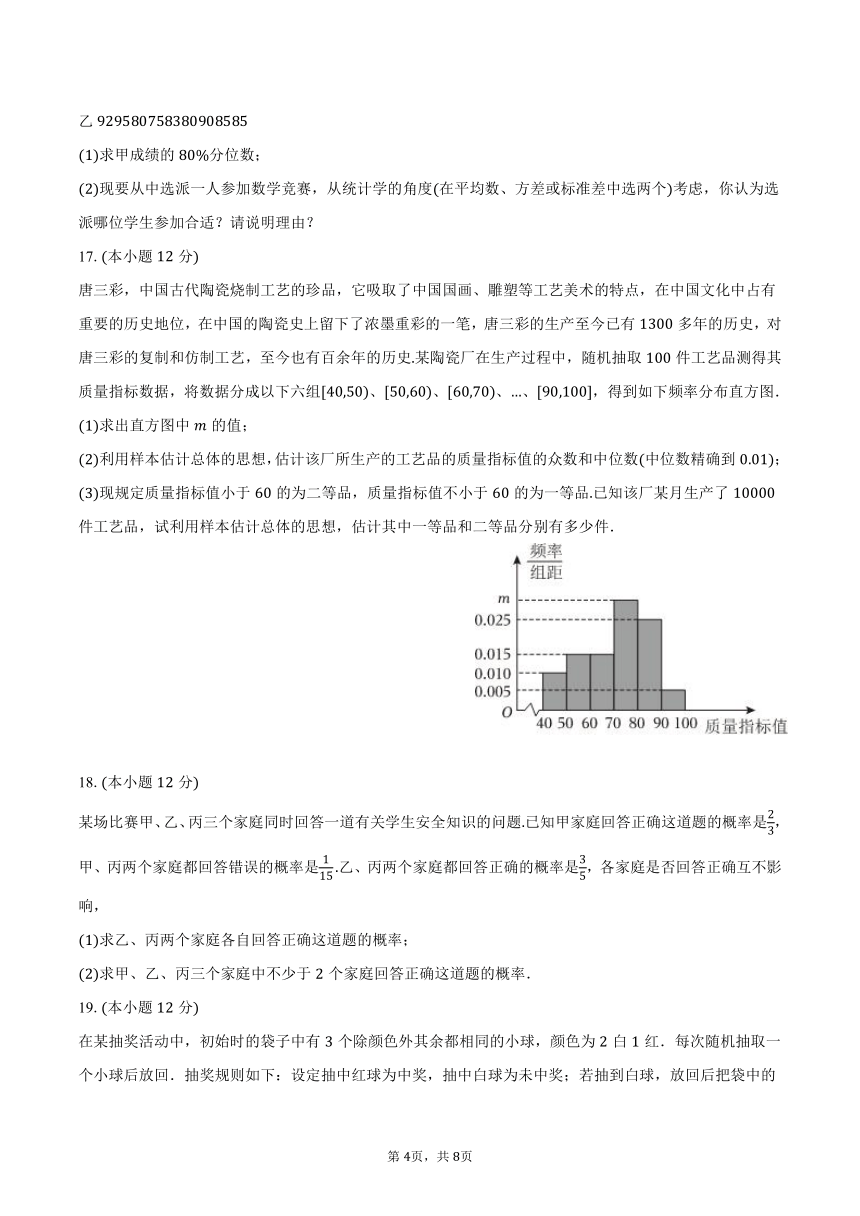
唐三彩,中国古代陶瓷烧制工艺的珍品,它吸取了中国国画、雕塑等工艺美术的特点,在中国文化中占有重要的历史地位,在中国的陶瓷史上留下了浓墨重彩的一笔,唐三彩的生产至今已有多年的历史,对唐三彩的复制和仿制工艺,至今也有百余年的历史某陶瓷厂在生产过程中,随机抽取件工艺品测得其质量指标数据,将数据分成以下六组、、、、,得到如下频率分布直方图.
求出直方图中的值;
利用样本估计总体的思想,估计该厂所生产的工艺品的质量指标值的众数和中位数中位数精确到;
现规定质量指标值小于的为二等品,质量指标值不小于的为一等品已知该厂某月生产了件工艺品,试利用样本估计总体的思想,估计其中一等品和二等品分别有多少件.
18.本小题分
某场比赛甲、乙、丙三个家庭同时回答一道有关学生安全知识的问题已知甲家庭回答正确这道题的概率是,甲、丙两个家庭都回答错误的概率是乙、丙两个家庭都回答正确的概率是,各家庭是否回答正确互不影响,
求乙、丙两个家庭各自回答正确这道题的概率;
求甲、乙、丙三个家庭中不少于个家庭回答正确这道题的概率.
19.本小题分
在某抽奖活动中,初始时的袋子中有个除颜色外其余都相同的小球,颜色为白红.每次随机抽取一个小球后放回.抽奖规则如下:设定抽中红球为中奖,抽中白球为未中奖;若抽到白球,放回后把袋中的一个白色小球替换为红色;若抽到红球,放回后把三个球的颜色重新变为白红的初始状态.记第次抽奖中奖的概率为.
求,;
若存在实数,,,对任意的不小于的正整数,都有,试确定,,的值,并证明上述递推公式;
若累计中奖次及以上可以获得一枚优胜者勋章,则从初始状态下连抽次获得至少一枚勋章的概率为多少?
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:由题意可知,,,,,,
,,,,,,
,;
,所以,不是互斥事件,
.
16.解:将甲的成绩从低到高排列如下:,,,,,,,,,
因为不是整数,所以选择第个数作为分位数,即.
甲成绩的平均数为,
甲成绩的方差为:
乙成绩的平均数为,
乙成绩的方差为:
.
因为,,甲的成绩比较稳定,所以派甲参加比较合适.
17.解:在频率分布直方图中,所有直方图的面积之和为,
则,得;
众数为,因为,,
所以中位数在第组,设中位数为,则,
解得.
所以,可以估计该厂所生产的工艺品的质量指标值的众数为,中位数为;
由频率分布直方图可知件工艺品中二等品有件,
一等品有件,
该厂生产的件工艺品中一等品有件,
二等品有件,
所以一等品有件,二等品有件.
18.解:记“甲家庭回答正确这道题”为事件,“乙家庭回答正确这道题”为事件,
“丙家庭回答正确这道题”为事件,
则,,,
即,,
所以,,
所以乙、丙两个家庭各自回答正确这道题的概率分别为,;
有个家庭回答正确的概率为,
有个家庭回答正确的概率为:
,
所以不少于个家庭回答正确这道题的概率.
19.解:由题意得,
;
因为每次中奖后袋中的球会回到初始状态,
从初始状态开始,若第一次中奖,此时第次抽奖中奖的概率为,
从初始状态开始,若第一次未中奖而第二次中奖,此时第次抽奖中奖的概率为,
从初始状态开始,若前两次均未中奖,则第三次必中奖,
此时第次抽奖中奖的概率为,
综上所述,对任意的,,
又,所以;
由题意知每抽三次至少有一次中奖,
故连抽次至少中奖次,
所以只需排除次中奖的情况即可获得一枚优胜者勋章,
另外,每两次中奖的间隔不能超过三次,每次中奖后袋中的球会回到初始状态,
从初始状态开始,抽一次中奖的概率为,
从初始状态开始抽两次,第一次未中奖而第二次中奖的概率为,
从初始状态开始抽三次,前两次均未中奖而第三次中奖的概率为,
用表示第次,第次,第次中奖,其余未中奖,
则三次中奖的所有情况如下:,
,
故仅三次中奖的概率为
,
所以从初始状态下连抽次获得至少一枚勋章的概率为.
第1页,共1页
数学试卷(9月份)
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.要调查下列问题,适合采用全面调查普查的是( )
A. 某城市居民月份人均网上购物的次数 B. 某品牌新能源汽车最大续航里程
C. 检测一批灯泡的使用寿命 D. 调查一个班级学生每周的体育锻炼时间
2.成飞中学高一年级人,高二年级人,现按比例分层随机抽样的方法从高一、高二年级抽取名同学朗诵“成飞赋”,则高二抽取的人数为( )
A. B. C. D.
3.下列说法一定正确的是 .
A. 一名篮球运动员,号称“百发百中”,若罚球三次,不会出现三投都不中的情况
B. 一个骰子掷一次得到的概率是,则掷次一定会出现一次
C. 若买彩票中奖的概率为万分之一,则买一万元的彩票一定会中奖一元
D. 随机事件发生的概率与试验次数无关
4.甲乙两人在相同条件下各打靶次,每次打靶的成绩情况如图所示:下列说法错误的是( )
A. 从平均数和方差相结合看,甲波动比较大,乙相对比较稳定
B. 从折线统计图上两人射击命中环数走势看,甲更有潜力
C. 从平均数和命中环及环以上的次数相结合看,甲成绩较好
D. 从平均数和中位数相结合看,乙成绩较好
5.续航能力关乎无人机的“生命力”,太阳能供能是实现无人机长时续航的重要路径之一.某大学科研团队利用自主开发的新型静电电机,成功研制出仅重克的太阳能动力微型无人机,实现纯自然光供能下的持续飞行.为激发同学们对无人机的兴趣,某校无人机兴趣社团在校内进行选拔赛,名参赛学生的成绩依次为,,,,,,,,则这组数据的上四分位数也叫第百分位数为( )
A. B. C. D.
6.【选考北师大版】小明在整理数据时得到了该组数据的平均数为,方差为,后来发现有两个数据记录有误,一个错将记录为,另一个错将记录为在对错误的数据进行更正后,重新求得该组数据的平均数为,方差为,则( )
A. , B. ,
C. , D. ,
7.在一个不透明的袋子里装有四个小球,球上分别标有,,,四个数字,这些小球除数字外都相同甲、乙两人玩“猜数字”游戏,甲先从袋中任意摸出一个小球,将小球上的数字记为,再由乙猜这个小球上的数字,记为如果,满足,那么就称甲、乙两人“心领神会”,则两人“心领神会”的概率是( )
A. B. C. D.
8.已知事件,,且,,则下列说法正确的是( )
A. 若,则,
B. 若与互斥,则,
C. 若与相互独立,则,
D. 若与相互独立,则,
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.甲、乙两人进行篮球比赛,若甲投中的概率为,乙投不中的概率为,且两人投篮互不影响,若两人各投篮一次,则下列结论中正确的是( )
A. 两人都投中的概率为 B. 至少一人投中的概率为
C. 至多一人投中的概率为 D. 恰好有一人投中的概率为
10.有两组样本数据,分别为,,,和,,,,且平均数,方差分别为和,将两组数据合并为,,,,重新计算平均数和方差,则( )
A. 平均数为 B. 平均数为 C. 方差为 D. 方差为
11.某保险公司为客户定制了个险种:甲,一年期短期;乙,两全保险;丙,理财类保险;丁,定期寿险;戊,重大疾病保险.各种保险按相关约定进行参保与理赔.该保险公司对个险种参保客户进行抽样调查,得到如图所示的统计图表.则( )
A. 丁险种参保人数超过五成 B. 岁以上参保人数超过总参保人数的五成
C. 周岁人群参保的总费用最少 D. 人均参保费用不超过元
三、填空题:本题共3小题,每小题5分,共15分。
12.已知某运动员每次投篮命中的概率都为,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算机产生到之间取整数值的随机数,指定,,,表示命中,,,,,,表示不命中;再以三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下组随机数:
据此估计,该运动员三次投篮恰有两次命中的概率为 .
13.若样本数据,,,的方差为,则数据,,,的方差为______.
14.若三个元件,,按照如图的方式连接成一个系统,每个元件是否正常工作不受其他元件的影响,当元件正常工作且,中至少有一个正常工作时,系统就正常工作,若元件,正常工作的概率依次为,,且这个系统正常工作的概率为,则元件正常工作的概率为______.
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
从,,,这四个数字中,不放回地取两次,每次取一个,构成数对,为第一次取到的数字,为第二次取到的数字设事件“第一次取出的数字是“,“第二次取出的数字是”.
写出此试验的样本空间及,的值;
判断与是不是互斥事件,并求的值.
16.本小题分
甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取次,记录如下:
甲
乙
求甲成绩的分位数;
现要从中选派一人参加数学竞赛,从统计学的角度在平均数、方差或标准差中选两个考虑,你认为选派哪位学生参加合适?请说明理由?
17.本小题分
唐三彩,中国古代陶瓷烧制工艺的珍品,它吸取了中国国画、雕塑等工艺美术的特点,在中国文化中占有重要的历史地位,在中国的陶瓷史上留下了浓墨重彩的一笔,唐三彩的生产至今已有多年的历史,对唐三彩的复制和仿制工艺,至今也有百余年的历史某陶瓷厂在生产过程中,随机抽取件工艺品测得其质量指标数据,将数据分成以下六组、、、、,得到如下频率分布直方图.
求出直方图中的值;
利用样本估计总体的思想,估计该厂所生产的工艺品的质量指标值的众数和中位数中位数精确到;
现规定质量指标值小于的为二等品,质量指标值不小于的为一等品已知该厂某月生产了件工艺品,试利用样本估计总体的思想,估计其中一等品和二等品分别有多少件.
18.本小题分
某场比赛甲、乙、丙三个家庭同时回答一道有关学生安全知识的问题已知甲家庭回答正确这道题的概率是,甲、丙两个家庭都回答错误的概率是乙、丙两个家庭都回答正确的概率是,各家庭是否回答正确互不影响,
求乙、丙两个家庭各自回答正确这道题的概率;
求甲、乙、丙三个家庭中不少于个家庭回答正确这道题的概率.
19.本小题分
在某抽奖活动中,初始时的袋子中有个除颜色外其余都相同的小球,颜色为白红.每次随机抽取一个小球后放回.抽奖规则如下:设定抽中红球为中奖,抽中白球为未中奖;若抽到白球,放回后把袋中的一个白色小球替换为红色;若抽到红球,放回后把三个球的颜色重新变为白红的初始状态.记第次抽奖中奖的概率为.
求,;
若存在实数,,,对任意的不小于的正整数,都有,试确定,,的值,并证明上述递推公式;
若累计中奖次及以上可以获得一枚优胜者勋章,则从初始状态下连抽次获得至少一枚勋章的概率为多少?
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:由题意可知,,,,,,
,,,,,,
,;
,所以,不是互斥事件,
.
16.解:将甲的成绩从低到高排列如下:,,,,,,,,,
因为不是整数,所以选择第个数作为分位数,即.
甲成绩的平均数为,
甲成绩的方差为:
乙成绩的平均数为,
乙成绩的方差为:
.
因为,,甲的成绩比较稳定,所以派甲参加比较合适.
17.解:在频率分布直方图中,所有直方图的面积之和为,
则,得;
众数为,因为,,
所以中位数在第组,设中位数为,则,
解得.
所以,可以估计该厂所生产的工艺品的质量指标值的众数为,中位数为;
由频率分布直方图可知件工艺品中二等品有件,
一等品有件,
该厂生产的件工艺品中一等品有件,
二等品有件,
所以一等品有件,二等品有件.
18.解:记“甲家庭回答正确这道题”为事件,“乙家庭回答正确这道题”为事件,
“丙家庭回答正确这道题”为事件,
则,,,
即,,
所以,,
所以乙、丙两个家庭各自回答正确这道题的概率分别为,;
有个家庭回答正确的概率为,
有个家庭回答正确的概率为:
,
所以不少于个家庭回答正确这道题的概率.
19.解:由题意得,
;
因为每次中奖后袋中的球会回到初始状态,
从初始状态开始,若第一次中奖,此时第次抽奖中奖的概率为,
从初始状态开始,若第一次未中奖而第二次中奖,此时第次抽奖中奖的概率为,
从初始状态开始,若前两次均未中奖,则第三次必中奖,
此时第次抽奖中奖的概率为,
综上所述,对任意的,,
又,所以;
由题意知每抽三次至少有一次中奖,
故连抽次至少中奖次,
所以只需排除次中奖的情况即可获得一枚优胜者勋章,
另外,每两次中奖的间隔不能超过三次,每次中奖后袋中的球会回到初始状态,
从初始状态开始,抽一次中奖的概率为,
从初始状态开始抽两次,第一次未中奖而第二次中奖的概率为,
从初始状态开始抽三次,前两次均未中奖而第三次中奖的概率为,
用表示第次,第次,第次中奖,其余未中奖,
则三次中奖的所有情况如下:,
,
故仅三次中奖的概率为
,
所以从初始状态下连抽次获得至少一枚勋章的概率为.
第1页,共1页
同课章节目录
