2024-2025学年湖南省“湖湘名校教育联合体”高一10月大联考数学(含答案)
文档属性
| 名称 | 2024-2025学年湖南省“湖湘名校教育联合体”高一10月大联考数学(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 46.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-17 00:00:00 | ||
图片预览


文档简介
2024-2025学年湖南省“湖湘名校教育联合体”高一10月大联考数学
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知命题,,则为( )
A. , B. ,
C. ,( ) D. ,
2.已知,,则的取值范围为( )
A. B. C. D.
3.已知全集,,则集合的非空真子集个数为( )
A. B. C. D.
4.已知,,则下列不等式恒成立的是( )
A. B. C. D.
5.已知命题,,命题,,则( )
A. 和都是真命题 B. 和都是真命题
C. 和都是真命题 D. 和都是真命题
6.已知命题,,若是的必要条件,则正整数的值为( )
A. B. C. D.
7.年月日上午,以“新质动力创绿未来”为主题的世界动力电池大会在万里长江第一城、中国动力电池之都----四川宜宾开幕,该大会发布了一系列新技术、新产品,有效凝聚了行业共识,为推动技术迭代、深化开放合作、促进产业集聚、助力绿色发展,以及动力电池及新能源汽车高质量发展作出了积极贡献,为此某高中对高一班全班男生进行了关于对人工智能、新能源汽车、绿色能源是否有兴趣的问卷调查,要求每位同学至少选择一项,经统计有人对人工智能感兴趣,人对新能源汽车感兴趣,人对绿色能源感兴趣,同时对人工智能和新能源汽车感兴趣的有人,同时对新能源汽车和绿色能源感兴趣的有人,同时对人工智能和绿色能源感兴趣的有人,三种都感兴趣的有人,则该班男生人数为( )
A. B. C. D.
8.已知,则的最小值为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.假设“集合学得好不等式学得就好”是真命题,那么下列命题正确的是( )
A. 集合学得好不等式不一定学得好 B. 不等式学得好集合不一定学得好
C. 不等式学得不好集合一定学得不好 D. 集合学得不好不等式一定学得不好
10.设集合,其中,则( )
A. B. C. D.
11.已知不等式的解集为,则( )
A. B.
C. D.
三、填空题:本题共3小题,每小题5分,共15分。
12.已知,则 .
13.已知集合,,且,则的取值范围是 .
14.若对任意的恒成立,则实数的取值集合为 .
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
设命题关于的方程有两个不相等的实数根,关于的方程无实数根.
若为真命题,求的取值范围
若为假命题且为真命题,求的取值范围.
16.本小题分
已知正数,满足.
求的最大值
证明:
17.本小题分
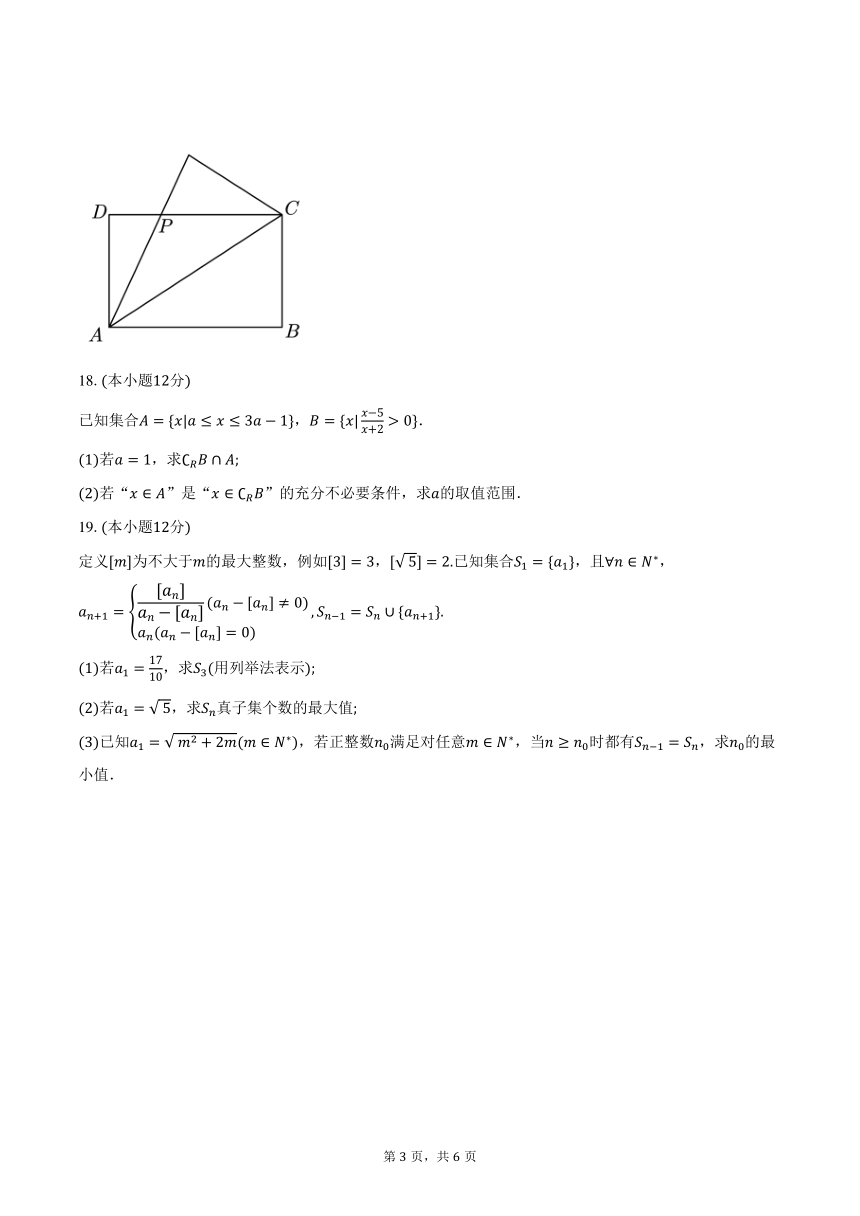
在学习完基本不等式与一元二次方程这一章节后,某校高一数学老师带领全班同学在数学课堂上做了一个有趣的实验,该实验的目的主要是体现不等式在实际生活中的应用老师要求同学们准备了一张周长为的矩形纸片其中,将沿向折叠,折过去后交于点如果在保持矩形周长不变且折过去后交于点的情况下,适度改变的长度,问:的面积是否存在最大值若存在,求出其最大值若不存在,说明理由.
18.本小题分
已知集合,.
若,求
若“”是“”的充分不必要条件,求的取值范围.
19.本小题分
定义为不大于的最大整数,例如,已知集合,且,
若,求用列举法表示
若,求真子集个数的最大值
已知,若正整数满足对任意,当时都有,求的最小值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:由题意关于的方程有两个不相等的实数根是真命题,
所以,即或.
由题意关于的方程无实数根是真命题,
所以,即.
因为为假命题且为真命题,
故,即.
综上所述,的取值范围为.
16.解:因为,所以,
故,即,故,
当且仅当、时等号成立
因为即,所以,
因为,所以,即,
当且仅当,时取等号.
17.解:由题意可知,矩形的周长为,设,则,设,
则,,由为直角三角形及勾股定理可得,
,.
.
当且仅当,即时取等,此时,满足,
故AB时,取最大面积.
18.解:由可得,解得或,
所以集合或,
时,集合,且,
故.
解法一:若“”是“”的充分不必要条件,故A是的真子集.
当时,,即时,满足是的真子集
当时,则满足且不能同时取等号,解得,
综上所述,的取值范围为
解法二:若“”是“”的充分不必要条件,故A是的真子集.
则只需满足且不能同时取等号,解得,
故的取值范围为
19.解:,则,,,
,,
,,故,,
,,故,,
,,故,,
则,,
故真子集个数的最大值为.
,故,,故,
,
由,,,,故,,且,
故,,故.
因为,所以
所以的最小值为.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知命题,,则为( )
A. , B. ,
C. ,( ) D. ,
2.已知,,则的取值范围为( )
A. B. C. D.
3.已知全集,,则集合的非空真子集个数为( )
A. B. C. D.
4.已知,,则下列不等式恒成立的是( )
A. B. C. D.
5.已知命题,,命题,,则( )
A. 和都是真命题 B. 和都是真命题
C. 和都是真命题 D. 和都是真命题
6.已知命题,,若是的必要条件,则正整数的值为( )
A. B. C. D.
7.年月日上午,以“新质动力创绿未来”为主题的世界动力电池大会在万里长江第一城、中国动力电池之都----四川宜宾开幕,该大会发布了一系列新技术、新产品,有效凝聚了行业共识,为推动技术迭代、深化开放合作、促进产业集聚、助力绿色发展,以及动力电池及新能源汽车高质量发展作出了积极贡献,为此某高中对高一班全班男生进行了关于对人工智能、新能源汽车、绿色能源是否有兴趣的问卷调查,要求每位同学至少选择一项,经统计有人对人工智能感兴趣,人对新能源汽车感兴趣,人对绿色能源感兴趣,同时对人工智能和新能源汽车感兴趣的有人,同时对新能源汽车和绿色能源感兴趣的有人,同时对人工智能和绿色能源感兴趣的有人,三种都感兴趣的有人,则该班男生人数为( )
A. B. C. D.
8.已知,则的最小值为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.假设“集合学得好不等式学得就好”是真命题,那么下列命题正确的是( )
A. 集合学得好不等式不一定学得好 B. 不等式学得好集合不一定学得好
C. 不等式学得不好集合一定学得不好 D. 集合学得不好不等式一定学得不好
10.设集合,其中,则( )
A. B. C. D.
11.已知不等式的解集为,则( )
A. B.
C. D.
三、填空题:本题共3小题,每小题5分,共15分。
12.已知,则 .
13.已知集合,,且,则的取值范围是 .
14.若对任意的恒成立,则实数的取值集合为 .
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
设命题关于的方程有两个不相等的实数根,关于的方程无实数根.
若为真命题,求的取值范围
若为假命题且为真命题,求的取值范围.
16.本小题分
已知正数,满足.
求的最大值
证明:
17.本小题分
在学习完基本不等式与一元二次方程这一章节后,某校高一数学老师带领全班同学在数学课堂上做了一个有趣的实验,该实验的目的主要是体现不等式在实际生活中的应用老师要求同学们准备了一张周长为的矩形纸片其中,将沿向折叠,折过去后交于点如果在保持矩形周长不变且折过去后交于点的情况下,适度改变的长度,问:的面积是否存在最大值若存在,求出其最大值若不存在,说明理由.
18.本小题分
已知集合,.
若,求
若“”是“”的充分不必要条件,求的取值范围.
19.本小题分
定义为不大于的最大整数,例如,已知集合,且,
若,求用列举法表示
若,求真子集个数的最大值
已知,若正整数满足对任意,当时都有,求的最小值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:由题意关于的方程有两个不相等的实数根是真命题,
所以,即或.
由题意关于的方程无实数根是真命题,
所以,即.
因为为假命题且为真命题,
故,即.
综上所述,的取值范围为.
16.解:因为,所以,
故,即,故,
当且仅当、时等号成立
因为即,所以,
因为,所以,即,
当且仅当,时取等号.
17.解:由题意可知,矩形的周长为,设,则,设,
则,,由为直角三角形及勾股定理可得,
,.
.
当且仅当,即时取等,此时,满足,
故AB时,取最大面积.
18.解:由可得,解得或,
所以集合或,
时,集合,且,
故.
解法一:若“”是“”的充分不必要条件,故A是的真子集.
当时,,即时,满足是的真子集
当时,则满足且不能同时取等号,解得,
综上所述,的取值范围为
解法二:若“”是“”的充分不必要条件,故A是的真子集.
则只需满足且不能同时取等号,解得,
故的取值范围为
19.解:,则,,,
,,
,,故,,
,,故,,
,,故,,
则,,
故真子集个数的最大值为.
,故,,故,
,
由,,,,故,,且,
故,,故.
因为,所以
所以的最小值为.
第1页,共1页
同课章节目录
