2025北师版高中数学必修第二册练习题--第6章 §6 6.2 柱、锥、台的体积(含解析)
文档属性
| 名称 | 2025北师版高中数学必修第二册练习题--第6章 §6 6.2 柱、锥、台的体积(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 399.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-18 23:21:47 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2025北师版高中数学必修第二册
6.2 柱、锥、台的体积
课后训练巩固提升
A组
1.已知直角三角形两直角边AB=3,AC=4,以AB所在直线为旋转轴,旋转一周所得的几何体的体积为( ).
A.12π B.16π
C.20π D.24π
2.设正六棱锥的底面边长为1,侧棱长为,那么它的体积为( ).
A.6 B.
C.2 D.2
3.已知圆台的上、下底面面积分别是π,4π,侧面积是6π,则这个圆台的体积是( ).
A.π B.2
C.π D.π
4.在三棱锥P-ABC中,线段PC上的点M满足PM=PC,线段PB上的点N满足PN=PB,则三棱锥P-AMN和三棱锥P-ABC的体积之比为( ).
A. B.
C. D.
5.若正方体的棱长为,则以该正方体各个面的中心为顶点的凸多面体的体积为( ).
A. B.
C. D.
6.一正四棱台的斜高与上、下底面边长之比为5∶2∶8,体积为14 cm3,则该棱台的高为 .
7.已知圆锥的轴截面是一个顶角为,腰长为2的等腰三角形,则该圆锥的体积为 .
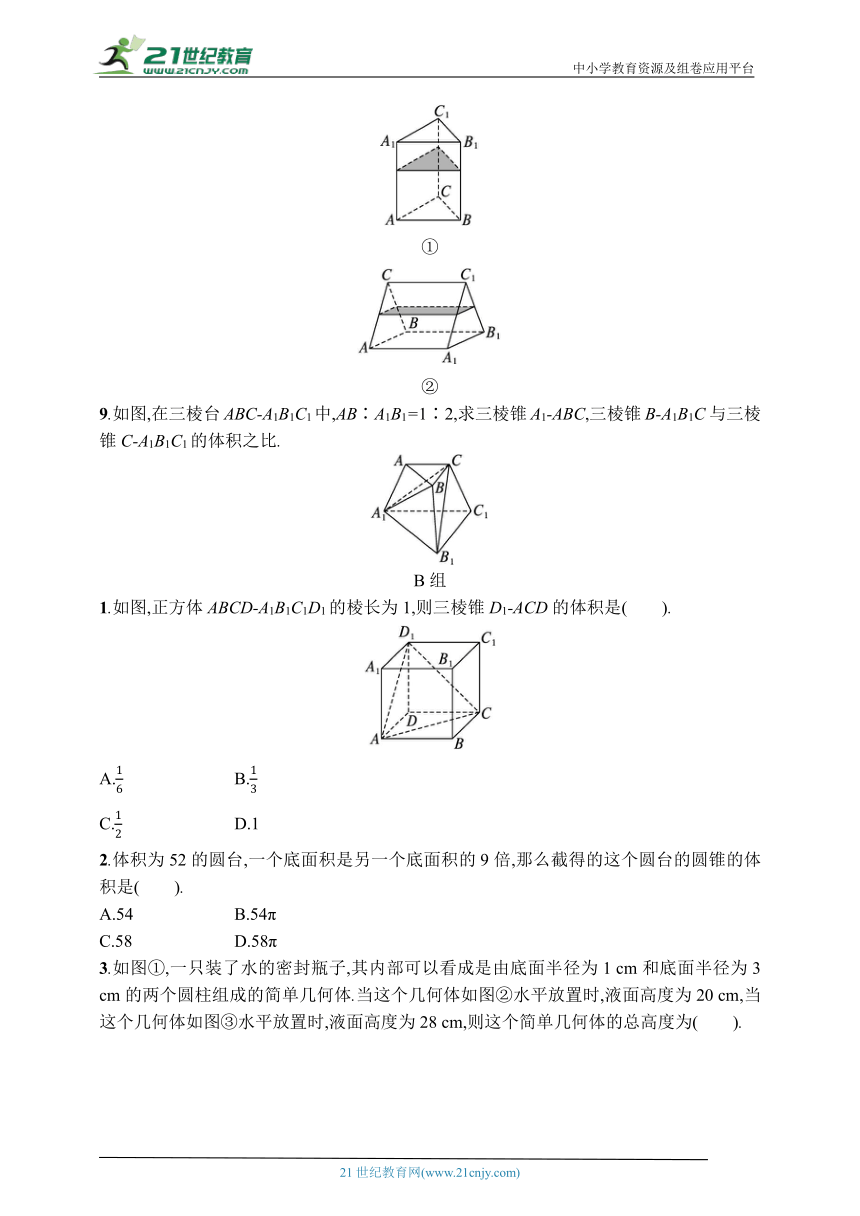
8.如图①,一个正三棱柱形容器,底面边长为a,高为2a,内装水若干,现将容器放倒,把一个侧面作为底面,这时水面恰好为中截面,如图②,则原来容器内水面的高度为 .
①
②
9.如图,在三棱台ABC-A1B1C1中,AB∶A1B1=1∶2,求三棱锥A1-ABC,三棱锥B-A1B1C与三棱锥C-A1B1C1的体积之比.
B组
1.如图,正方体ABCD-A1B1C1D1的棱长为1,则三棱锥D1-ACD的体积是( ).
A. B.
C. D.1
2.体积为52的圆台,一个底面积是另一个底面积的9倍,那么截得的这个圆台的圆锥的体积是( ).
A.54 B.54π
C.58 D.58π
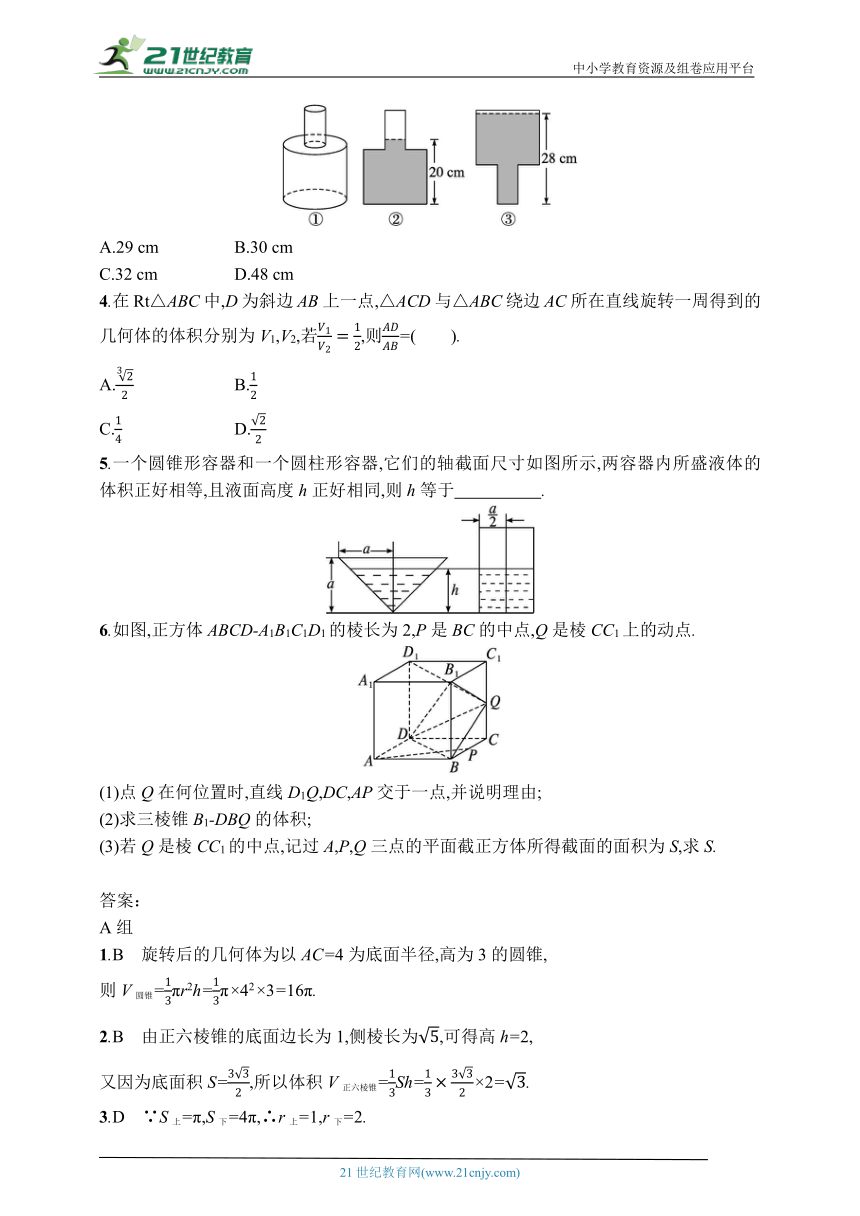
3.如图①,一只装了水的密封瓶子,其内部可以看成是由底面半径为1 cm和底面半径为3 cm的两个圆柱组成的简单几何体.当这个几何体如图②水平放置时,液面高度为20 cm,当这个几何体如图③水平放置时,液面高度为28 cm,则这个简单几何体的总高度为( ).
A.29 cm B.30 cm
C.32 cm D.48 cm
4.在Rt△ABC中,D为斜边AB上一点,△ACD与△ABC绕边AC所在直线旋转一周得到的几何体的体积分别为V1,V2,若,则=( ).
A. B.
C. D.
5.一个圆锥形容器和一个圆柱形容器,它们的轴截面尺寸如图所示,两容器内所盛液体的体积正好相等,且液面高度h正好相同,则h等于 .
6.如图,正方体ABCD-A1B1C1D1的棱长为2,P是BC的中点,Q是棱CC1上的动点.
(1)点Q在何位置时,直线D1Q,DC,AP交于一点,并说明理由;
(2)求三棱锥B1-DBQ的体积;
(3)若Q是棱CC1的中点,记过A,P,Q三点的平面截正方体所得截面的面积为S,求S.
答案:
A组
1.B 旋转后的几何体为以AC=4为底面半径,高为3的圆锥,
则V圆锥=πr2h=π×42×3=16π.
2.B 由正六棱锥的底面边长为1,侧棱长为,可得高h=2,
又因为底面积S=,所以体积V正六棱锥=Sh=×2=.
3.D ∵S上=π,S下=4π,∴r上=1,r下=2.
又S侧=6π=π(r上+r下)l,∴l=2.∴h=.
∴V圆台=π(1+4+2)×π.故选D.
4.B 如图,将三棱锥P-AMN看作三棱锥A-PMN,即以A为顶点,△PMN为底面的三棱锥,将三棱锥P-ABC看作三棱锥A-PBC,即以A为顶点,△PBC为底面的三棱锥.
因为S△PBC=PB·PC·sin∠BPC,S△PMN=PN·PM·sin∠NPM,而PN=PB,PM=PC,∠BPC=∠NPM,所以S△PMN=S△PBC=S△PBC,点A到底面PBC的距离和点A 到底面PMN的距离相等,设为h,故.故选B.
5.B 由题意知,以正方体各个面的中心为顶点的凸多面体是由两个同底等高的正四棱锥组成的,其中所有的棱长均为1,可得两个正四棱锥的高均为,故此多面体的体积V=2V正四棱锥=2××12×.故选B.
6.2 cm 由题意可设该正四棱台的斜高与上、下底面边长分别为5x cm,2x cm,8x cm,则高h==4x(cm).由棱台的体积公式,得·4x·(4x2+16x2+64x2)=14,解得x=,故h=2 cm.
7.π 因为圆锥的轴截面是一个顶角为,腰长为2的等腰三角形,所以此等腰三角形底边上的高即为圆锥的高h=2cos=1,圆锥底面圆半径r=,所以该圆锥的体积V=πr2h=π××1=π.
8.a 设题图①中容器内水面的高度为h,水的体积为V,则V=S△ABC·h.
又题图②中水组成了一个直四棱柱,由题意知
其底面积为S△ABC,高度为2a,所以V=S△ABC·2a,即S△ABC·h=S△ABC·2a.解得h=a.
9.解 设棱台的高为h,S△ABC=S,则=4S,
∴S△ABC·h=Sh,
·h=Sh.
又V台体=h(S+4S+2S)=Sh,
∴=V台体-Sh-Sh.∴所求体积比为1∶2∶4.
B组
1.A 三棱锥D1-ADC的体积V=S△ADC·D1D=·AD·DC·D1D=×1×1×1=.
2.A 设上底面半径为r,则由题意可得下底面半径为3r,
设圆台高为h1,则πh1(r2+9r2+3r·r)=52,
∴πr2h1=12.设原圆锥的高为h,则由相似知识得,∴h=h1.
∴V原圆锥=π(3r)2×h=3πr2×h1=×12=54.
3.A 在题图②和题图③中,瓶子上部没有液体的部分容积相等,设这个简单几何体的总高度为h,则有π×12×(h-20)=π×32×(h-28),解得h=29 cm.
4.D 令=λ,BC=a,AC=b,
作ED∥BC,交AC于点E,则=λ,ED=λa,EC=b-λb,AE=λb,
所以V2=πa2·b,V1=πλ2a2·λb+πλ2a2(b-λb)=πλ2a2·b,
所以=λ2=,所以λ=,故选D.
5.a 设圆锥形容器的液面的半径为R,则液体的体积为πR2h,圆柱形容器内的液体体积为πh.
根据题意,有πR2h=πh,解得R=a.
再根据圆锥形容器的轴截面与内盛液体轴截面是相似三角形,得,所以h=a.
6.解 (1)当Q是棱CC1的中点时,直线D1Q,DC,AP交于一点.理由如下:如图,延长D1Q,DC交于点O,则QC为△DD1O的中位线,
所以C为DO的中点.延长AP,DC交于点O',则PC为△ADO'的中位线,所以C为DO'的中点.
所以点O与点O'重合.所以直线D1Q,DC,AP交于一点.
(2)×2=.
(3)如图,连接AD1,PQ,由(1)知,D1Q,AP交于一点,故点D1,Q,A,P确定一个平面.
因为平面ADD1A1∥平面BCC1B1,且平面APQD1分别与两平面相交,交线为AD1,PQ,
所以AD1∥PQ,
所以梯形APQD1为所求截面,梯形APQD1的高为,
故S=+2)×.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025北师版高中数学必修第二册
6.2 柱、锥、台的体积
课后训练巩固提升
A组
1.已知直角三角形两直角边AB=3,AC=4,以AB所在直线为旋转轴,旋转一周所得的几何体的体积为( ).
A.12π B.16π
C.20π D.24π
2.设正六棱锥的底面边长为1,侧棱长为,那么它的体积为( ).
A.6 B.
C.2 D.2
3.已知圆台的上、下底面面积分别是π,4π,侧面积是6π,则这个圆台的体积是( ).
A.π B.2
C.π D.π
4.在三棱锥P-ABC中,线段PC上的点M满足PM=PC,线段PB上的点N满足PN=PB,则三棱锥P-AMN和三棱锥P-ABC的体积之比为( ).
A. B.
C. D.
5.若正方体的棱长为,则以该正方体各个面的中心为顶点的凸多面体的体积为( ).
A. B.
C. D.
6.一正四棱台的斜高与上、下底面边长之比为5∶2∶8,体积为14 cm3,则该棱台的高为 .
7.已知圆锥的轴截面是一个顶角为,腰长为2的等腰三角形,则该圆锥的体积为 .
8.如图①,一个正三棱柱形容器,底面边长为a,高为2a,内装水若干,现将容器放倒,把一个侧面作为底面,这时水面恰好为中截面,如图②,则原来容器内水面的高度为 .
①
②
9.如图,在三棱台ABC-A1B1C1中,AB∶A1B1=1∶2,求三棱锥A1-ABC,三棱锥B-A1B1C与三棱锥C-A1B1C1的体积之比.
B组
1.如图,正方体ABCD-A1B1C1D1的棱长为1,则三棱锥D1-ACD的体积是( ).
A. B.
C. D.1
2.体积为52的圆台,一个底面积是另一个底面积的9倍,那么截得的这个圆台的圆锥的体积是( ).
A.54 B.54π
C.58 D.58π
3.如图①,一只装了水的密封瓶子,其内部可以看成是由底面半径为1 cm和底面半径为3 cm的两个圆柱组成的简单几何体.当这个几何体如图②水平放置时,液面高度为20 cm,当这个几何体如图③水平放置时,液面高度为28 cm,则这个简单几何体的总高度为( ).
A.29 cm B.30 cm
C.32 cm D.48 cm
4.在Rt△ABC中,D为斜边AB上一点,△ACD与△ABC绕边AC所在直线旋转一周得到的几何体的体积分别为V1,V2,若,则=( ).
A. B.
C. D.
5.一个圆锥形容器和一个圆柱形容器,它们的轴截面尺寸如图所示,两容器内所盛液体的体积正好相等,且液面高度h正好相同,则h等于 .
6.如图,正方体ABCD-A1B1C1D1的棱长为2,P是BC的中点,Q是棱CC1上的动点.
(1)点Q在何位置时,直线D1Q,DC,AP交于一点,并说明理由;
(2)求三棱锥B1-DBQ的体积;
(3)若Q是棱CC1的中点,记过A,P,Q三点的平面截正方体所得截面的面积为S,求S.
答案:
A组
1.B 旋转后的几何体为以AC=4为底面半径,高为3的圆锥,
则V圆锥=πr2h=π×42×3=16π.
2.B 由正六棱锥的底面边长为1,侧棱长为,可得高h=2,
又因为底面积S=,所以体积V正六棱锥=Sh=×2=.
3.D ∵S上=π,S下=4π,∴r上=1,r下=2.
又S侧=6π=π(r上+r下)l,∴l=2.∴h=.
∴V圆台=π(1+4+2)×π.故选D.
4.B 如图,将三棱锥P-AMN看作三棱锥A-PMN,即以A为顶点,△PMN为底面的三棱锥,将三棱锥P-ABC看作三棱锥A-PBC,即以A为顶点,△PBC为底面的三棱锥.
因为S△PBC=PB·PC·sin∠BPC,S△PMN=PN·PM·sin∠NPM,而PN=PB,PM=PC,∠BPC=∠NPM,所以S△PMN=S△PBC=S△PBC,点A到底面PBC的距离和点A 到底面PMN的距离相等,设为h,故.故选B.
5.B 由题意知,以正方体各个面的中心为顶点的凸多面体是由两个同底等高的正四棱锥组成的,其中所有的棱长均为1,可得两个正四棱锥的高均为,故此多面体的体积V=2V正四棱锥=2××12×.故选B.
6.2 cm 由题意可设该正四棱台的斜高与上、下底面边长分别为5x cm,2x cm,8x cm,则高h==4x(cm).由棱台的体积公式,得·4x·(4x2+16x2+64x2)=14,解得x=,故h=2 cm.
7.π 因为圆锥的轴截面是一个顶角为,腰长为2的等腰三角形,所以此等腰三角形底边上的高即为圆锥的高h=2cos=1,圆锥底面圆半径r=,所以该圆锥的体积V=πr2h=π××1=π.
8.a 设题图①中容器内水面的高度为h,水的体积为V,则V=S△ABC·h.
又题图②中水组成了一个直四棱柱,由题意知
其底面积为S△ABC,高度为2a,所以V=S△ABC·2a,即S△ABC·h=S△ABC·2a.解得h=a.
9.解 设棱台的高为h,S△ABC=S,则=4S,
∴S△ABC·h=Sh,
·h=Sh.
又V台体=h(S+4S+2S)=Sh,
∴=V台体-Sh-Sh.∴所求体积比为1∶2∶4.
B组
1.A 三棱锥D1-ADC的体积V=S△ADC·D1D=·AD·DC·D1D=×1×1×1=.
2.A 设上底面半径为r,则由题意可得下底面半径为3r,
设圆台高为h1,则πh1(r2+9r2+3r·r)=52,
∴πr2h1=12.设原圆锥的高为h,则由相似知识得,∴h=h1.
∴V原圆锥=π(3r)2×h=3πr2×h1=×12=54.
3.A 在题图②和题图③中,瓶子上部没有液体的部分容积相等,设这个简单几何体的总高度为h,则有π×12×(h-20)=π×32×(h-28),解得h=29 cm.
4.D 令=λ,BC=a,AC=b,
作ED∥BC,交AC于点E,则=λ,ED=λa,EC=b-λb,AE=λb,
所以V2=πa2·b,V1=πλ2a2·λb+πλ2a2(b-λb)=πλ2a2·b,
所以=λ2=,所以λ=,故选D.
5.a 设圆锥形容器的液面的半径为R,则液体的体积为πR2h,圆柱形容器内的液体体积为πh.
根据题意,有πR2h=πh,解得R=a.
再根据圆锥形容器的轴截面与内盛液体轴截面是相似三角形,得,所以h=a.
6.解 (1)当Q是棱CC1的中点时,直线D1Q,DC,AP交于一点.理由如下:如图,延长D1Q,DC交于点O,则QC为△DD1O的中位线,
所以C为DO的中点.延长AP,DC交于点O',则PC为△ADO'的中位线,所以C为DO'的中点.
所以点O与点O'重合.所以直线D1Q,DC,AP交于一点.
(2)×2=.
(3)如图,连接AD1,PQ,由(1)知,D1Q,AP交于一点,故点D1,Q,A,P确定一个平面.
因为平面ADD1A1∥平面BCC1B1,且平面APQD1分别与两平面相交,交线为AD1,PQ,
所以AD1∥PQ,
所以梯形APQD1为所求截面,梯形APQD1的高为,
故S=+2)×.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
