2025北师版高中数学必修第二册练习题--第1章 §3 弧度制(含解析)
文档属性
| 名称 | 2025北师版高中数学必修第二册练习题--第1章 §3 弧度制(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 350.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-19 10:14:22 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025北师版高中数学必修第二册
§3 弧度制
课后训练巩固提升
A组
1.(多选题)下列各角中与240°角终边相同的角有( ).
A. B.-
C.- D.
2.若θ=-5,则角θ的终边所在的象限是( ).
A.第四象限
B.第三象限
C.第二象限
D.第一象限
3.集合中的角所表示的范围(阴影部分)是( ).
4.已知角的顶点与原点重合,始边与x轴的非负半轴重合,则下列各组角中,表示终边相同的角的是( ).
A.2kπ±与kπ±(k∈Z)
B.kπ±与2kπ+(k∈Z)
C.kπ-与kπ+(k∈Z)
D.2kπ±π与kπ(k∈Z)
5.在[0,2π]范围内,与终边相同的角为 .
6.时针经过一小时,转过了 rad.
7.用弧度表示终边落在如图所示阴影部分内(不包括边界)的角的集合.
8.已知集合A=[-],B={β∣2kπ+<β≤2kπ+,k∈Z},C={γ|-10<γ<10}.
(1)若θ∈A,且角3θ与-θ的终边垂直,求θ;
(2)求B∩C.
B组
1.(多选题)下列表示中正确的是( ).
A.终边在x轴上的角的集合是{α|α=kπ,k∈Z}
B.终边在y轴上的角的集合是{α∣α=+kπ,k∈Z}
C.终边在坐标轴上的角的集合是{α∣α=k·,k∈Z}
D.终边在直线y=x上的角的集合是{α∣α=+2kπ,k∈Z}
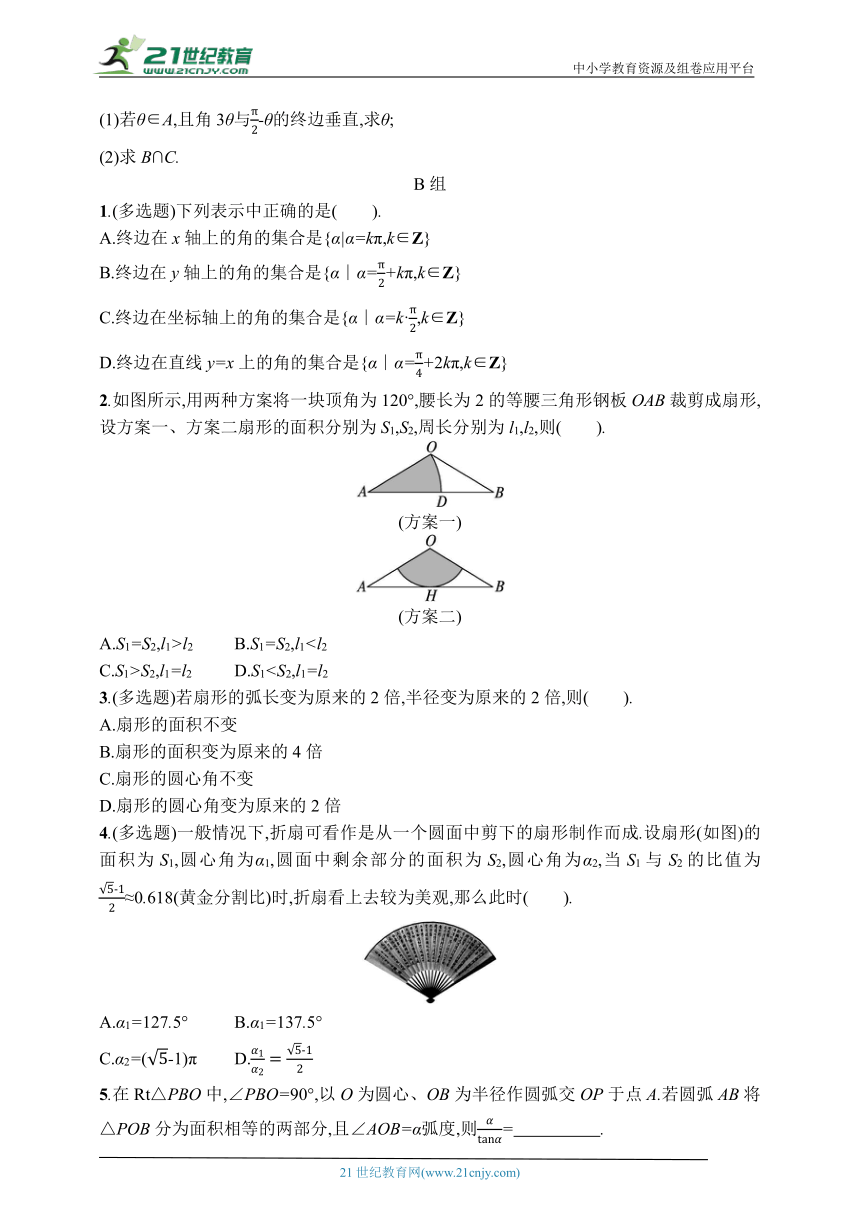
2.如图所示,用两种方案将一块顶角为120°,腰长为2的等腰三角形钢板OAB裁剪成扇形,设方案一、方案二扇形的面积分别为S1,S2,周长分别为l1,l2,则( ).
(方案一)
(方案二)
A.S1=S2,l1>l2 B.S1=S2,l1C.S1>S2,l1=l2 D.S13.(多选题)若扇形的弧长变为原来的2倍,半径变为原来的2倍,则( ).
A.扇形的面积不变
B.扇形的面积变为原来的4倍
C.扇形的圆心角不变
D.扇形的圆心角变为原来的2倍
4.(多选题)一般情况下,折扇可看作是从一个圆面中剪下的扇形制作而成.设扇形(如图)的面积为S1,圆心角为α1,圆面中剩余部分的面积为S2,圆心角为α2,当S1与S2的比值为≈0.618(黄金分割比)时,折扇看上去较为美观,那么此时( ).
A.α1=127.5° B.α1=137.5°
C.α2=(-1)π D.
5.在Rt△PBO中,∠PBO=90°,以O为圆心、OB为半径作圆弧交OP于点A.若圆弧AB将△POB分为面积相等的两部分,且∠AOB=α弧度,则= .
6.某企业欲做一个介绍企业发展史的广告牌,广告牌的截面形状是如图所示的扇形环面(由扇形OAD挖去扇形OBC后构成的).已知OA=10 m,OB=x m(0(1)求θ关于x的函数解析式.
(2)记广告牌的截面面积为y,试问x取何值时,y的值最大 并求出最大值.
答案:
A组
1.CD 240°=,而--2π,+2π.故选CD.
2.D 因为-2π<-5<-,所以角θ的终边在第一象限.
3.C 当k=2m,m∈Z时,2mπ+≤α≤2mπ+,m∈Z;当k=2m+1,m∈Z时,2mπ+≤α≤2mπ+,m∈Z.故选C.
4.C 对于A,当k=1时,kπ+,在2kπ±(k∈Z)表示的角中不存在与终边相同的角,不符合题意;对于B,kπ±(k∈Z)表示终边在y轴上的角,2kπ+(k∈Z)表示终边在y轴非负半轴上的角,不符合题意;对于C,kπ-(k∈Z),kπ+(k∈Z)表示终边在y轴上的角,符合题意;对于D,2kπ±π(k∈Z)表示终边在x轴非正半轴上的角,kπ(k∈Z)表示终边在x轴上的角,不符合题意.故选C.
5. 与终边相同的角为β=+2kπ,k∈Z,
令0≤+2kπ≤2π,k∈Z,得-≤k≤-,k∈Z,所以k=-3,β=-6π=,
所以在[0,2π]范围内,与终边相同的角为.
6.- 时针经过一小时,转过-30°,-30°=- rad.
7.解 如题图,330°角的终边与-30°角的终边相同,将-30°化为弧度,即-,而75°=75×,故终边落在阴影部分内(不包括边界)的角的集合为{θ<θ<2kπ+,k∈Z}.
8.解 (1)由3θ与-θ终边垂直,
可得3θ=-θ++kπ,k∈Z,得θ=,k∈Z,又θ∈A,故θ的所有可能取值为-,-,0,.
(2)B={β|2kπ+<β≤2kπ+,k∈Z},
当k=-1时,B={β|-<β≤-},
当k=0时,B={β|<β≤},
当k=1时,B={β|<β≤},
又C={γ|-10<γ<10},
∴B∩C=∪(]∪(].
B组
1.ABC 终边在直线y=x上的角的集合是{α|α=+kπ,k∈Z},D错误.易知ABC正确.
2.A ∵△AOB是顶角为120°,腰长为2的等腰三角形,
∴∠A=∠B=30°=,OH=1,
方案一中扇形的周长l1=2+2+2×=4+,方案二中扇形的周长l2=1+1+1×=2+,方案一中扇形的面积S1=×2×2×,方案二中扇形的面积S2=×12×,故S1=S2,l1>l2.
3.BC 设原扇形的半径为r,弧长为l,圆心角为α,则原扇形的面积为S1=lr,扇形的弧长变为原来的2倍,半径变为原来的2倍后,其面积为S2=·2l·2r=2lr,故S2=4S1,故A错误,B正确;由α=,可知扇形的圆心角不变,故C正确,D错误.
4.BCD 设扇形的半径为R,则,故D正确;
因为α1+α2=2π,所以α2+α2=2π,解得α2=(-1)π,故C正确;
由≈0.618,则-1≈1.236,
所以α2=(-1)π≈1.236×180°≈222.5°,
所以α1≈360°-222.5°=137.5°,故B正确.
5. 设扇形的半径为r,
则扇形的面积为αr2.
在Rt△POB中,PB=rtan α,
则△POB的面积为r·rtan α.
由题意得r·rtan α=2×αr2,
即tan α=2α,
故.
6.解 (1)根据题意,可算得=x·θ,=10θ.
因为BA+CD+=30,
所以10-x+10-x+xθ+10θ=30.
所以θ=(0(2)依据题意,可知y=S扇形OAD-S扇形OBC=θ×102-θx2,
化简得y=-x2+5x+50=-.
所以当x=时,ymax=.
答:当x=时,y的值最大,且最大值为 m2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025北师版高中数学必修第二册
§3 弧度制
课后训练巩固提升
A组
1.(多选题)下列各角中与240°角终边相同的角有( ).
A. B.-
C.- D.
2.若θ=-5,则角θ的终边所在的象限是( ).
A.第四象限
B.第三象限
C.第二象限
D.第一象限
3.集合中的角所表示的范围(阴影部分)是( ).
4.已知角的顶点与原点重合,始边与x轴的非负半轴重合,则下列各组角中,表示终边相同的角的是( ).
A.2kπ±与kπ±(k∈Z)
B.kπ±与2kπ+(k∈Z)
C.kπ-与kπ+(k∈Z)
D.2kπ±π与kπ(k∈Z)
5.在[0,2π]范围内,与终边相同的角为 .
6.时针经过一小时,转过了 rad.
7.用弧度表示终边落在如图所示阴影部分内(不包括边界)的角的集合.
8.已知集合A=[-],B={β∣2kπ+<β≤2kπ+,k∈Z},C={γ|-10<γ<10}.
(1)若θ∈A,且角3θ与-θ的终边垂直,求θ;
(2)求B∩C.
B组
1.(多选题)下列表示中正确的是( ).
A.终边在x轴上的角的集合是{α|α=kπ,k∈Z}
B.终边在y轴上的角的集合是{α∣α=+kπ,k∈Z}
C.终边在坐标轴上的角的集合是{α∣α=k·,k∈Z}
D.终边在直线y=x上的角的集合是{α∣α=+2kπ,k∈Z}
2.如图所示,用两种方案将一块顶角为120°,腰长为2的等腰三角形钢板OAB裁剪成扇形,设方案一、方案二扇形的面积分别为S1,S2,周长分别为l1,l2,则( ).
(方案一)
(方案二)
A.S1=S2,l1>l2 B.S1=S2,l1
A.扇形的面积不变
B.扇形的面积变为原来的4倍
C.扇形的圆心角不变
D.扇形的圆心角变为原来的2倍
4.(多选题)一般情况下,折扇可看作是从一个圆面中剪下的扇形制作而成.设扇形(如图)的面积为S1,圆心角为α1,圆面中剩余部分的面积为S2,圆心角为α2,当S1与S2的比值为≈0.618(黄金分割比)时,折扇看上去较为美观,那么此时( ).
A.α1=127.5° B.α1=137.5°
C.α2=(-1)π D.
5.在Rt△PBO中,∠PBO=90°,以O为圆心、OB为半径作圆弧交OP于点A.若圆弧AB将△POB分为面积相等的两部分,且∠AOB=α弧度,则= .
6.某企业欲做一个介绍企业发展史的广告牌,广告牌的截面形状是如图所示的扇形环面(由扇形OAD挖去扇形OBC后构成的).已知OA=10 m,OB=x m(0
(2)记广告牌的截面面积为y,试问x取何值时,y的值最大 并求出最大值.
答案:
A组
1.CD 240°=,而--2π,+2π.故选CD.
2.D 因为-2π<-5<-,所以角θ的终边在第一象限.
3.C 当k=2m,m∈Z时,2mπ+≤α≤2mπ+,m∈Z;当k=2m+1,m∈Z时,2mπ+≤α≤2mπ+,m∈Z.故选C.
4.C 对于A,当k=1时,kπ+,在2kπ±(k∈Z)表示的角中不存在与终边相同的角,不符合题意;对于B,kπ±(k∈Z)表示终边在y轴上的角,2kπ+(k∈Z)表示终边在y轴非负半轴上的角,不符合题意;对于C,kπ-(k∈Z),kπ+(k∈Z)表示终边在y轴上的角,符合题意;对于D,2kπ±π(k∈Z)表示终边在x轴非正半轴上的角,kπ(k∈Z)表示终边在x轴上的角,不符合题意.故选C.
5. 与终边相同的角为β=+2kπ,k∈Z,
令0≤+2kπ≤2π,k∈Z,得-≤k≤-,k∈Z,所以k=-3,β=-6π=,
所以在[0,2π]范围内,与终边相同的角为.
6.- 时针经过一小时,转过-30°,-30°=- rad.
7.解 如题图,330°角的终边与-30°角的终边相同,将-30°化为弧度,即-,而75°=75×,故终边落在阴影部分内(不包括边界)的角的集合为{θ<θ<2kπ+,k∈Z}.
8.解 (1)由3θ与-θ终边垂直,
可得3θ=-θ++kπ,k∈Z,得θ=,k∈Z,又θ∈A,故θ的所有可能取值为-,-,0,.
(2)B={β|2kπ+<β≤2kπ+,k∈Z},
当k=-1时,B={β|-<β≤-},
当k=0时,B={β|<β≤},
当k=1时,B={β|<β≤},
又C={γ|-10<γ<10},
∴B∩C=∪(]∪(].
B组
1.ABC 终边在直线y=x上的角的集合是{α|α=+kπ,k∈Z},D错误.易知ABC正确.
2.A ∵△AOB是顶角为120°,腰长为2的等腰三角形,
∴∠A=∠B=30°=,OH=1,
方案一中扇形的周长l1=2+2+2×=4+,方案二中扇形的周长l2=1+1+1×=2+,方案一中扇形的面积S1=×2×2×,方案二中扇形的面积S2=×12×,故S1=S2,l1>l2.
3.BC 设原扇形的半径为r,弧长为l,圆心角为α,则原扇形的面积为S1=lr,扇形的弧长变为原来的2倍,半径变为原来的2倍后,其面积为S2=·2l·2r=2lr,故S2=4S1,故A错误,B正确;由α=,可知扇形的圆心角不变,故C正确,D错误.
4.BCD 设扇形的半径为R,则,故D正确;
因为α1+α2=2π,所以α2+α2=2π,解得α2=(-1)π,故C正确;
由≈0.618,则-1≈1.236,
所以α2=(-1)π≈1.236×180°≈222.5°,
所以α1≈360°-222.5°=137.5°,故B正确.
5. 设扇形的半径为r,
则扇形的面积为αr2.
在Rt△POB中,PB=rtan α,
则△POB的面积为r·rtan α.
由题意得r·rtan α=2×αr2,
即tan α=2α,
故.
6.解 (1)根据题意,可算得=x·θ,=10θ.
因为BA+CD+=30,
所以10-x+10-x+xθ+10θ=30.
所以θ=(0
化简得y=-x2+5x+50=-.
所以当x=时,ymax=.
答:当x=时,y的值最大,且最大值为 m2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
