12.2.2全等三角形的判定SAS同步巩固练(含答案)2024--2025学年上学期初中数学人教版八年级上册
文档属性
| 名称 | 12.2.2全等三角形的判定SAS同步巩固练(含答案)2024--2025学年上学期初中数学人教版八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 498.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-18 00:00:00 | ||
图片预览



文档简介
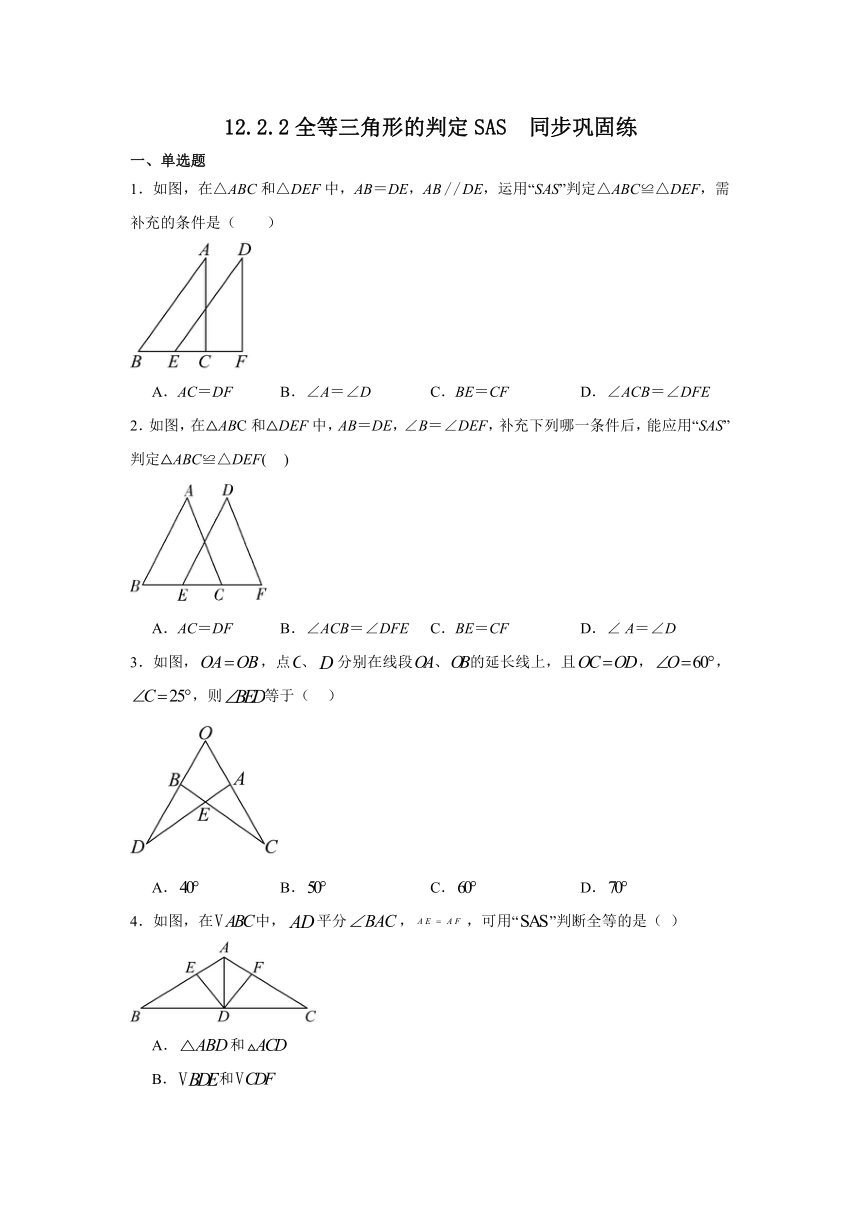
12.2.2全等三角形的判定SAS 同步巩固练
一、单选题
1.如图,在△ABC和△DEF中,AB=DE,ABDE,运用“SAS”判定△ABC≌△DEF,需补充的条件是( )
A.AC=DF B.∠A=∠D C.BE=CF D.∠ACB=∠DFE
2.如图,在△ABC和△DEF中,AB=DE,∠B=∠DEF,补充下列哪一条件后,能应用“SAS”判定△ABC≌△DEF( )
A.AC=DF B.∠ACB=∠DFE C.BE=CF D.∠ A=∠D
3.如图,,点、分别在线段、的延长线上,且,,,则等于( )
A. B. C. D.
4.如图,在中,平分,,可用“”判断全等的是( )
A.和
B.和
C.和
D.以上三个选项都可以
5.如图,把两个角的直角三角板放在一起,点B在上,A、C、D三点在一条直线上,连接延长线交于点F.若,则的面积为( )
A.16 B.12.8 C.6.4 D.5.6
6.如图所示,,,,B,D,E三点在一条直线上,若,,则的度数为( )
A. B. C. D.
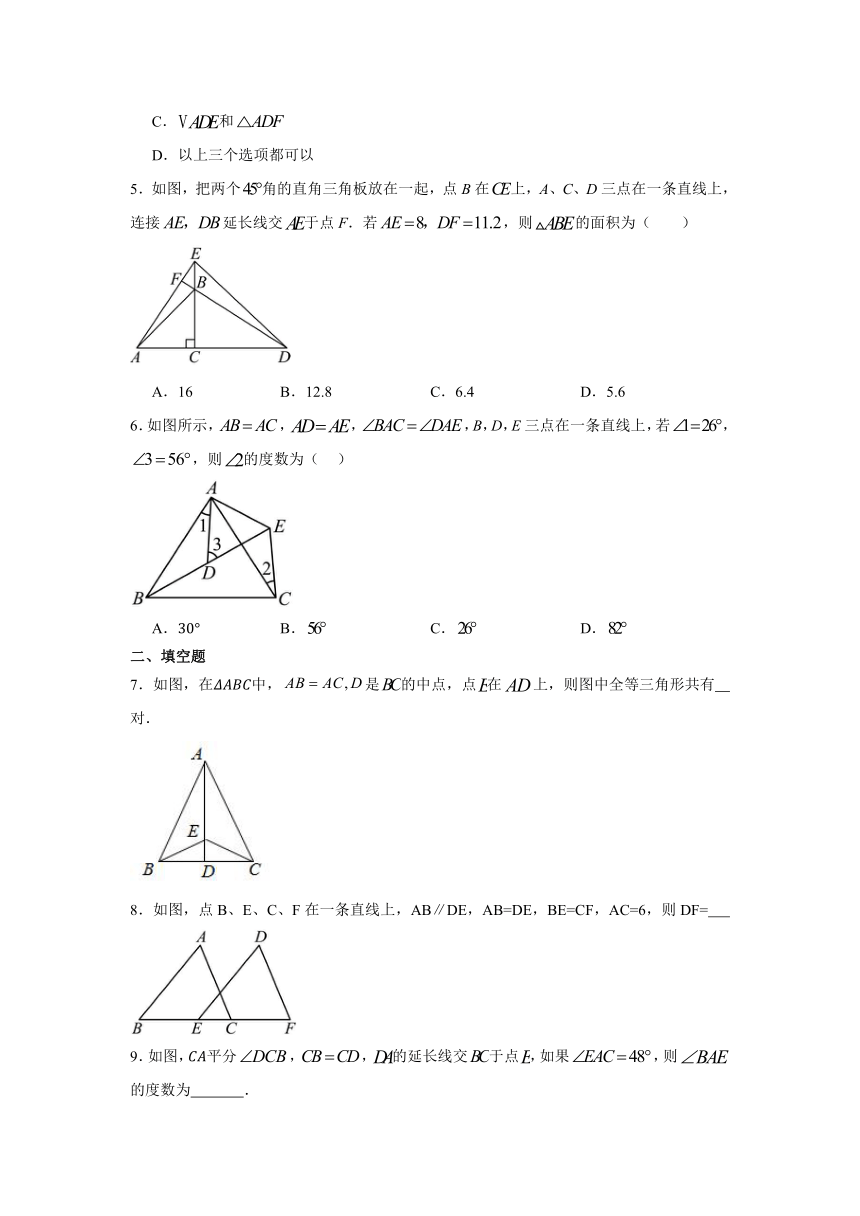
二、填空题
7.如图,在中,是的中点,点在上,则图中全等三角形共有 对.
8.如图,点B、E、C、F在一条直线上,AB∥DE,AB=DE,BE=CF,AC=6,则DF=
9.如图,平分,,的延长线交于点,如果,则的度数为 .
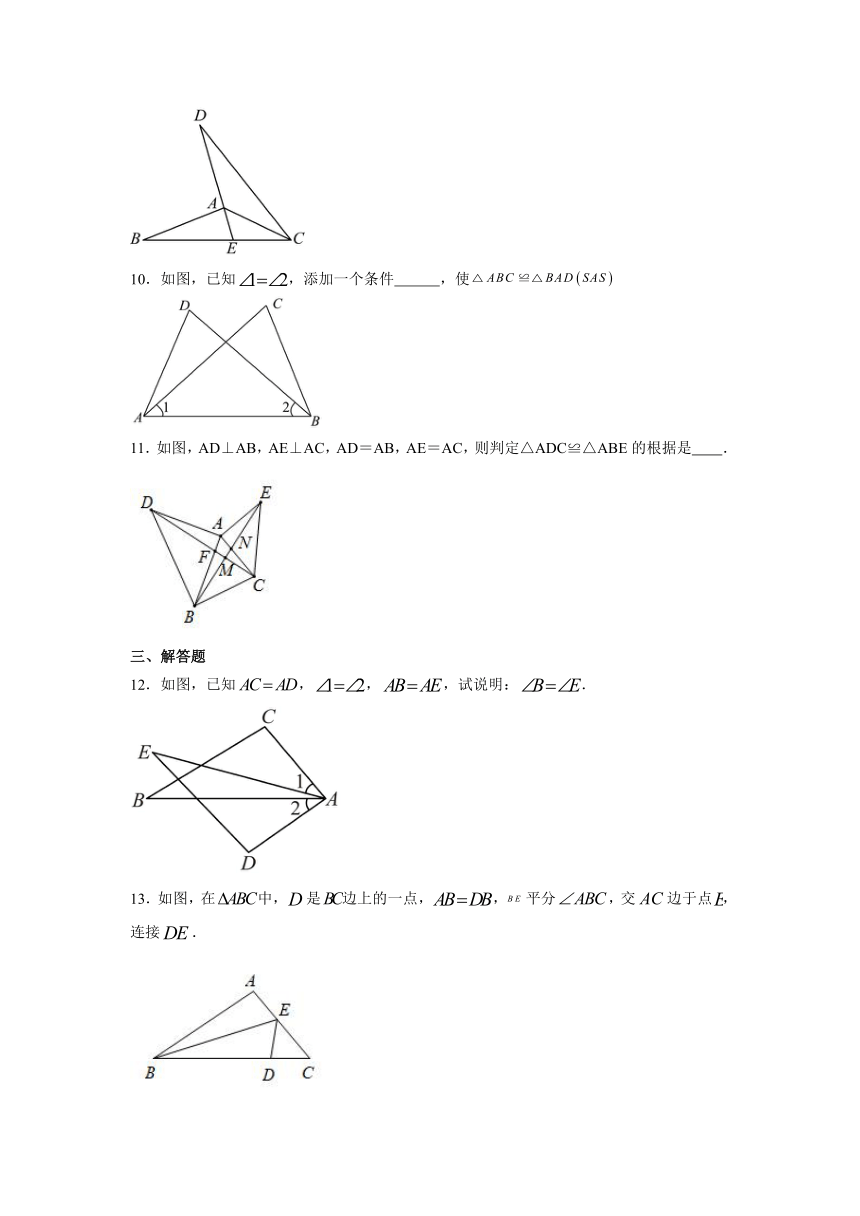
10.如图,已知,添加一个条件 ,使
11.如图,AD⊥AB,AE⊥AC,AD=AB,AE=AC,则判定△ADC≌△ABE的根据是 .
三、解答题
12.如图,已知,,,试说明:.
13.如图,在中,是边上的一点,,平分,交边于点,连接.
(1)求证:;
(2)若,,求的度数.
14.如图,在中,为上一点,为中点,连接并延长至点使得,连.
(1)求证:;
(2)若,连接,平分,平分,求的度数.
15.如图,已知;
求证:.
证明:(_______________)
即_______________
(_______________)
在和中
(_______________)
(_______________)
参考答案:
1.C
解:补充BE=CF,理由如下:
∵AB∥DE,
∴∠ABC=∠DEF,
若要利用SAS判定,B、D选项不符合要求,
若A:AC=DF,构成的是SSA,不能证明三角形全等,A选项不符合要求,
C选项:BE=CF,
∵BE=CF,
∴BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
2.C
∵∠B的两边是AB、BC,∠E的两边是DE、EF,AB=DE,
∴应用“SAS”判定△ABC≌△DEF,则BC=EF,
∵BC=BE+EC、EF= CF +EC,∴BE=CF.故选C.
3.D
解:在和中,
,
,
在中,,
4.C
解:∵平分,
∴,
在与中,
,
∴,
5.B
解:∵和都是等腰直角三角形,,
∴
在和中,
,
∴,
∴,
∴,
∴
∵,
∴,
∴
6.A
∵,
∴,
即,
在和中,
,
∴,
∴,
∵,
∴,
∵,
∴,
7.
解:图中的全等三角形有:△ABD≌△ACD,△ABE≌△ACE,△BDE≌△CDE;
∵D是BC的中点,
∴BD=DC,AB=AC,AD=AD,
∴△ABD≌△ACD(SSS);
∵AB=AC,点D为BC的中点,
∴AE为∠BAC的平分线,即∠BAE=∠CAE,
在△ABE和△ACE中,
∵AE=AE,∠BAE=∠CAE,AB=AC,
∴△ABE≌△ACE;
∵△ABE≌△ACE,
∴BE=CE,
在△BDE和△CDE中,
∵BE=CE,BD=DC,DE=DE,
∴△BDE≌△CDE.
综上,共有3对全等三角形,
故答案为:3.
8.6.
∵AB∥DE,
∴∠B=∠DEF
∵BE=CF,
∴BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴AC=DF=6.
9./84度
解:∵平分,
∴,
在和中,
,
∴,
∴,
∴,
∵,
∴,
∴,
故答案为:.
10.
解:∵△ABC与△BAD,具有AB=BA,和,一边和一角对应相等,
根据SAS判定两三角形确定,需添加夹角的另一边,
∴添加AC=BD,
在△ABC和△BAD中,
,
∴
故答案是:AC=BD.
11.SAS
∵AD⊥AB,AE⊥AC,
∴∠DAB=∠EAC=90°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
即:∠DAC=∠BAE,
在△ADC和△ABE中,
AD=AB,∠DAC=∠BAE,AE=AC,
∴△ADC≌△ABE(SAS),
故填:SAS.
12.详见解析
解:∵,
∴,
即,
在和中,
,
∴,
∴.
13.(1)见解析
(2)
(1)证明:∵平分,
∴,
在和中
∴;
(2)解:∵,
∴
由(1)可知,
∴,
∴.
14.(1)见解析
(2)
(1)证明:为中点,
,
在和中,
,
,
,
;
(2),
,
∵
,
平分,
,
,
,
的度数为.
15.已知;;;两直线平行,内错角相等;;全等三角形的对应边相等
】证明:(已知)
即
(两直线平行,内错角相等)
在和中
()
(全等三角形的对应边相等)
故答案为:已知;;;两直线平行,内错角相等;;全等三角形的对应边相等
一、单选题
1.如图,在△ABC和△DEF中,AB=DE,ABDE,运用“SAS”判定△ABC≌△DEF,需补充的条件是( )
A.AC=DF B.∠A=∠D C.BE=CF D.∠ACB=∠DFE
2.如图,在△ABC和△DEF中,AB=DE,∠B=∠DEF,补充下列哪一条件后,能应用“SAS”判定△ABC≌△DEF( )
A.AC=DF B.∠ACB=∠DFE C.BE=CF D.∠ A=∠D
3.如图,,点、分别在线段、的延长线上,且,,,则等于( )
A. B. C. D.
4.如图,在中,平分,,可用“”判断全等的是( )
A.和
B.和
C.和
D.以上三个选项都可以
5.如图,把两个角的直角三角板放在一起,点B在上,A、C、D三点在一条直线上,连接延长线交于点F.若,则的面积为( )
A.16 B.12.8 C.6.4 D.5.6
6.如图所示,,,,B,D,E三点在一条直线上,若,,则的度数为( )
A. B. C. D.
二、填空题
7.如图,在中,是的中点,点在上,则图中全等三角形共有 对.
8.如图,点B、E、C、F在一条直线上,AB∥DE,AB=DE,BE=CF,AC=6,则DF=
9.如图,平分,,的延长线交于点,如果,则的度数为 .
10.如图,已知,添加一个条件 ,使
11.如图,AD⊥AB,AE⊥AC,AD=AB,AE=AC,则判定△ADC≌△ABE的根据是 .
三、解答题
12.如图,已知,,,试说明:.
13.如图,在中,是边上的一点,,平分,交边于点,连接.
(1)求证:;
(2)若,,求的度数.
14.如图,在中,为上一点,为中点,连接并延长至点使得,连.
(1)求证:;
(2)若,连接,平分,平分,求的度数.
15.如图,已知;
求证:.
证明:(_______________)
即_______________
(_______________)
在和中
(_______________)
(_______________)
参考答案:
1.C
解:补充BE=CF,理由如下:
∵AB∥DE,
∴∠ABC=∠DEF,
若要利用SAS判定,B、D选项不符合要求,
若A:AC=DF,构成的是SSA,不能证明三角形全等,A选项不符合要求,
C选项:BE=CF,
∵BE=CF,
∴BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
2.C
∵∠B的两边是AB、BC,∠E的两边是DE、EF,AB=DE,
∴应用“SAS”判定△ABC≌△DEF,则BC=EF,
∵BC=BE+EC、EF= CF +EC,∴BE=CF.故选C.
3.D
解:在和中,
,
,
在中,,
4.C
解:∵平分,
∴,
在与中,
,
∴,
5.B
解:∵和都是等腰直角三角形,,
∴
在和中,
,
∴,
∴,
∴,
∴
∵,
∴,
∴
6.A
∵,
∴,
即,
在和中,
,
∴,
∴,
∵,
∴,
∵,
∴,
7.
解:图中的全等三角形有:△ABD≌△ACD,△ABE≌△ACE,△BDE≌△CDE;
∵D是BC的中点,
∴BD=DC,AB=AC,AD=AD,
∴△ABD≌△ACD(SSS);
∵AB=AC,点D为BC的中点,
∴AE为∠BAC的平分线,即∠BAE=∠CAE,
在△ABE和△ACE中,
∵AE=AE,∠BAE=∠CAE,AB=AC,
∴△ABE≌△ACE;
∵△ABE≌△ACE,
∴BE=CE,
在△BDE和△CDE中,
∵BE=CE,BD=DC,DE=DE,
∴△BDE≌△CDE.
综上,共有3对全等三角形,
故答案为:3.
8.6.
∵AB∥DE,
∴∠B=∠DEF
∵BE=CF,
∴BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴AC=DF=6.
9./84度
解:∵平分,
∴,
在和中,
,
∴,
∴,
∴,
∵,
∴,
∴,
故答案为:.
10.
解:∵△ABC与△BAD,具有AB=BA,和,一边和一角对应相等,
根据SAS判定两三角形确定,需添加夹角的另一边,
∴添加AC=BD,
在△ABC和△BAD中,
,
∴
故答案是:AC=BD.
11.SAS
∵AD⊥AB,AE⊥AC,
∴∠DAB=∠EAC=90°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
即:∠DAC=∠BAE,
在△ADC和△ABE中,
AD=AB,∠DAC=∠BAE,AE=AC,
∴△ADC≌△ABE(SAS),
故填:SAS.
12.详见解析
解:∵,
∴,
即,
在和中,
,
∴,
∴.
13.(1)见解析
(2)
(1)证明:∵平分,
∴,
在和中
∴;
(2)解:∵,
∴
由(1)可知,
∴,
∴.
14.(1)见解析
(2)
(1)证明:为中点,
,
在和中,
,
,
,
;
(2),
,
∵
,
平分,
,
,
,
的度数为.
15.已知;;;两直线平行,内错角相等;;全等三角形的对应边相等
】证明:(已知)
即
(两直线平行,内错角相等)
在和中
()
(全等三角形的对应边相等)
故答案为:已知;;;两直线平行,内错角相等;;全等三角形的对应边相等
