沪科版初中数学八年级下册教案 19.2 平行四边形
文档属性
| 名称 | 沪科版初中数学八年级下册教案 19.2 平行四边形 |  | |
| 格式 | zip | ||
| 文件大小 | 57.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-26 11:29:03 | ||
图片预览



文档简介
19.2平行四边形
教学目标: 1、掌握平行四边形的两种判定方法:两组对边分别平行的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形.
2、通过学生操作、作图探索并掌握判定四边形为平行四边形的条件。
3、培养学生合作探究问题的能力
教学重难点
重点:理解并掌握一组对边平行且相等的四边形是平行四边形这个判定定理
难点:平行四边形判定定理1的证明与应用
教具准备:三角板,直尺 幻灯片
教学过程
(一)创设情境、导入新课
我们前一段时间学行四边形的性质,同学们还能不能说出这些性质呢?(指名回答)
我们知道了平行四边形有很多重要的性质,但是一个四边形到底是不是平行四边形呢?我们如何来判断一个四边形是不是平行四边形?
板书:平行四边形的判定
(二)合作探究、学习新知
1、师生共同完成对平行四边形定义的回顾
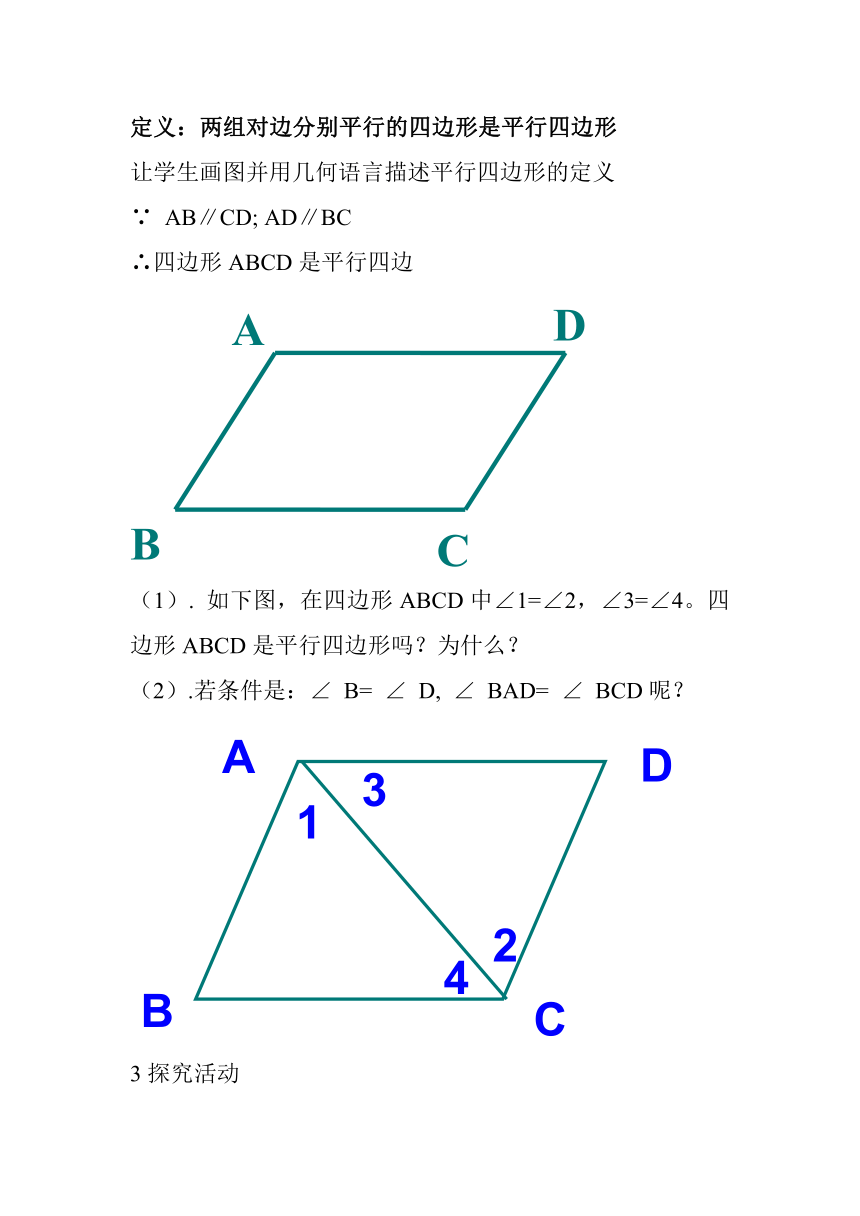
定义:两组对边分别平行的四边形是平行四边形
让学生画图并用几何语言描述平行四边形的定义
∵ AB∥CD; AD∥BC
∴四边形ABCD是平行四边
(1). 如下图,在四边形ABCD中∠1=∠2,∠3=∠4。四边形ABCD是平行四边形吗?为什么?
(2).若条件是:∠ B= ∠ D, ∠ BAD= ∠ BCD呢?
3探究活动
活动一:在练习本上放两根互相平行并且相等的细纸条AB、CD,连结AD、BC.
四边形ABCD是平行四边形吗?
学生分小组讨论后指名学生用文字语言表述上述活动事实,教师总结
一组对边平行且相等的四边形是平行四边形.
学生分小组讨论如何用几何语言表述上述事实
∵AD=BC, AD∥BC
∴四边形ABCD是平行四边形
探究定理
定理1、一组对边平行且相等的四边形是平行四边形
已知: 如图,在四边形ABCD中AD=BC, AD∥BC
求证: 四边形ABCD是平行四边形.
学生完成操作
学生思考
想一想:一组对边平行,而另一组对边相等的四边形是不是平行四边形?
6、合作探究例1
例1 在平行四边形ABCD中,
已知:M和N分别是AB和DC上的中点,
试证明:四边形BNDM也是平行四边形.
学生思考例1的证明
分小组讨论思考的结果
教师点评并给出证明(幻灯片给出)
证明:
∵ 四边形ABCD是平行四边形
∴ AB∥DC, AB=DC (平行四边形的对边平行且相等)
又∵ M和N分别是AB和DC上的中点
∴ BM∥DN, BM=DN
∴ 四边形BNDM也是平行四边形.
(一组对边平行且相等的四边形是平行四边形)
(4)学生思考上述证明过程并思考有没有其他种办法证明
(三)、互动交流、运用性质
1、变式 2
已知:如图,在□ABCD中,E、F分别是AB,CD的中点。
求证:EF∥AD∥BC。
2、变式3
如图,□ABCD中,E、F分别在BA、DC的延长线上,且AE=1/2 AB,CF=1/2 CD,
试说明AF和CE的关系如何?并说明理由。
如图,AC∥ED,点B在AC上
且AB=ED=BC 。
试找出图中的平行四边形.
4、如图,D、E是△ABC的边AB和AC中点,延长DE到F,使EF=DE,连结CF.四边形BCFD是平行四边形吗?为什么?
练一练
1. 对于四边形ABCD,如果从条件①AB∥CD
②AD∥BC③AB=CD④BC=AD中选出2个,
那么能 说明四边形ABCD是平行四边形的有
_______(填序号,填出符合条件的一种情
况即可)
2.若四边形ABCD , AD∥BC,
则只需添加一个
条件_____,能说明四边形ABCD是平行四边形
(四)合作小结、自主评价、
通过这节课的学习活动,你有哪些收获?给你印象最深的是什么?你还有哪些想法和疑惑?
教师幻灯片出示
四边形是平行四边形的条件
两组对边分别平行的四边形是平行四边形.
∵AD∥BC,DC∥AB,
∴ABCD是平行四边形.
2. 一组对边平行且相等的四边形是平行四边形.
∵ AB=DC,AB ∥ DC,
∴ ABCD是平行四边形.
(五)作业
1、教材P82页练习第1、2题; 2、习题19.2第9题
附板书设计
定义 两组对边分别平行的四边形是平行四边形
定理1、一组对边平行且相等的四边形是平行四边形
已知:如图AD=BC, AD∥BC
求证:四边形ABCD是平行四边形
证明:连接A、C两点
∵AD∥BC
∴∠DAC=∠BCA
在△DAC和△DAC中
AD=BC
∠DAC=∠BCA
AC=CA
∴△DAC≌△DAC
∴∠DCA=∠BAC
∴DC∥AB
∵AD∥BC
四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
公开课教案
课题:19.2平行四边形
寿县板桥中心学校
孙怀进
2014年11月
B
C
A
D
A
B
C
D
1
2
3
4
A
C
B
D
A
F
E
D
C
B
A
C
B
E
D
A
C
B
D
A
B
C
D
教学目标: 1、掌握平行四边形的两种判定方法:两组对边分别平行的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形.
2、通过学生操作、作图探索并掌握判定四边形为平行四边形的条件。
3、培养学生合作探究问题的能力
教学重难点
重点:理解并掌握一组对边平行且相等的四边形是平行四边形这个判定定理
难点:平行四边形判定定理1的证明与应用
教具准备:三角板,直尺 幻灯片
教学过程
(一)创设情境、导入新课
我们前一段时间学行四边形的性质,同学们还能不能说出这些性质呢?(指名回答)
我们知道了平行四边形有很多重要的性质,但是一个四边形到底是不是平行四边形呢?我们如何来判断一个四边形是不是平行四边形?
板书:平行四边形的判定
(二)合作探究、学习新知
1、师生共同完成对平行四边形定义的回顾
定义:两组对边分别平行的四边形是平行四边形
让学生画图并用几何语言描述平行四边形的定义
∵ AB∥CD; AD∥BC
∴四边形ABCD是平行四边
(1). 如下图,在四边形ABCD中∠1=∠2,∠3=∠4。四边形ABCD是平行四边形吗?为什么?
(2).若条件是:∠ B= ∠ D, ∠ BAD= ∠ BCD呢?
3探究活动
活动一:在练习本上放两根互相平行并且相等的细纸条AB、CD,连结AD、BC.
四边形ABCD是平行四边形吗?
学生分小组讨论后指名学生用文字语言表述上述活动事实,教师总结
一组对边平行且相等的四边形是平行四边形.
学生分小组讨论如何用几何语言表述上述事实
∵AD=BC, AD∥BC
∴四边形ABCD是平行四边形
探究定理
定理1、一组对边平行且相等的四边形是平行四边形
已知: 如图,在四边形ABCD中AD=BC, AD∥BC
求证: 四边形ABCD是平行四边形.
学生完成操作
学生思考
想一想:一组对边平行,而另一组对边相等的四边形是不是平行四边形?
6、合作探究例1
例1 在平行四边形ABCD中,
已知:M和N分别是AB和DC上的中点,
试证明:四边形BNDM也是平行四边形.
学生思考例1的证明
分小组讨论思考的结果
教师点评并给出证明(幻灯片给出)
证明:
∵ 四边形ABCD是平行四边形
∴ AB∥DC, AB=DC (平行四边形的对边平行且相等)
又∵ M和N分别是AB和DC上的中点
∴ BM∥DN, BM=DN
∴ 四边形BNDM也是平行四边形.
(一组对边平行且相等的四边形是平行四边形)
(4)学生思考上述证明过程并思考有没有其他种办法证明
(三)、互动交流、运用性质
1、变式 2
已知:如图,在□ABCD中,E、F分别是AB,CD的中点。
求证:EF∥AD∥BC。
2、变式3
如图,□ABCD中,E、F分别在BA、DC的延长线上,且AE=1/2 AB,CF=1/2 CD,
试说明AF和CE的关系如何?并说明理由。
如图,AC∥ED,点B在AC上
且AB=ED=BC 。
试找出图中的平行四边形.
4、如图,D、E是△ABC的边AB和AC中点,延长DE到F,使EF=DE,连结CF.四边形BCFD是平行四边形吗?为什么?
练一练
1. 对于四边形ABCD,如果从条件①AB∥CD
②AD∥BC③AB=CD④BC=AD中选出2个,
那么能 说明四边形ABCD是平行四边形的有
_______(填序号,填出符合条件的一种情
况即可)
2.若四边形ABCD , AD∥BC,
则只需添加一个
条件_____,能说明四边形ABCD是平行四边形
(四)合作小结、自主评价、
通过这节课的学习活动,你有哪些收获?给你印象最深的是什么?你还有哪些想法和疑惑?
教师幻灯片出示
四边形是平行四边形的条件
两组对边分别平行的四边形是平行四边形.
∵AD∥BC,DC∥AB,
∴ABCD是平行四边形.
2. 一组对边平行且相等的四边形是平行四边形.
∵ AB=DC,AB ∥ DC,
∴ ABCD是平行四边形.
(五)作业
1、教材P82页练习第1、2题; 2、习题19.2第9题
附板书设计
定义 两组对边分别平行的四边形是平行四边形
定理1、一组对边平行且相等的四边形是平行四边形
已知:如图AD=BC, AD∥BC
求证:四边形ABCD是平行四边形
证明:连接A、C两点
∵AD∥BC
∴∠DAC=∠BCA
在△DAC和△DAC中
AD=BC
∠DAC=∠BCA
AC=CA
∴△DAC≌△DAC
∴∠DCA=∠BAC
∴DC∥AB
∵AD∥BC
四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
公开课教案
课题:19.2平行四边形
寿县板桥中心学校
孙怀进
2014年11月
B
C
A
D
A
B
C
D
1
2
3
4
A
C
B
D
A
F
E
D
C
B
A
C
B
E
D
A
C
B
D
A
B
C
D
