沪科版初中数学九下第24章24.2圆的基本性质(共23张PPT)
文档属性
| 名称 | 沪科版初中数学九下第24章24.2圆的基本性质(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 595.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-28 00:00:00 | ||
图片预览




文档简介
课件23张PPT。24.2 圆的基本性质
圆心角、弧、弦、弦心距之间的关系1、复习垂径定理及其推论。 (知二推三)
2、理解圆心角的概念.
3、掌握圆心角、弧、弦、弦心距之间的相等关系定理及推论. (知一推三)
4、理解“1°的弧”的概念。学习目标:垂径定理 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.题设结论(1)直径
(2)垂直于弦}{(3)平分弦
(4)平分弦所对的优弧
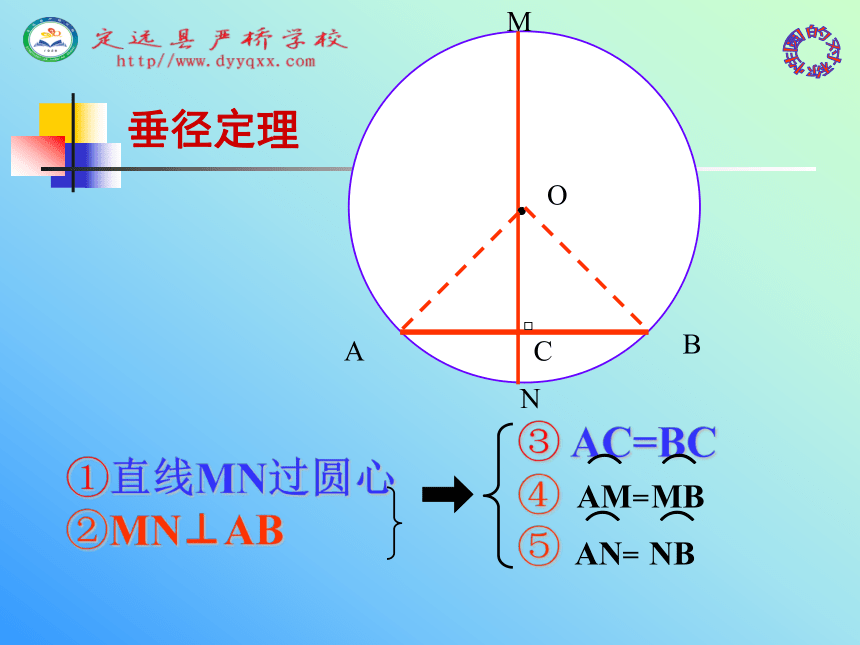
(5)平分弦所对的劣弧MOACBN①直线MN过圆心②MN⊥AB③ AC=BC
④ ⑤垂径定理MOACBN①直线MN过圆心③ AC=BC
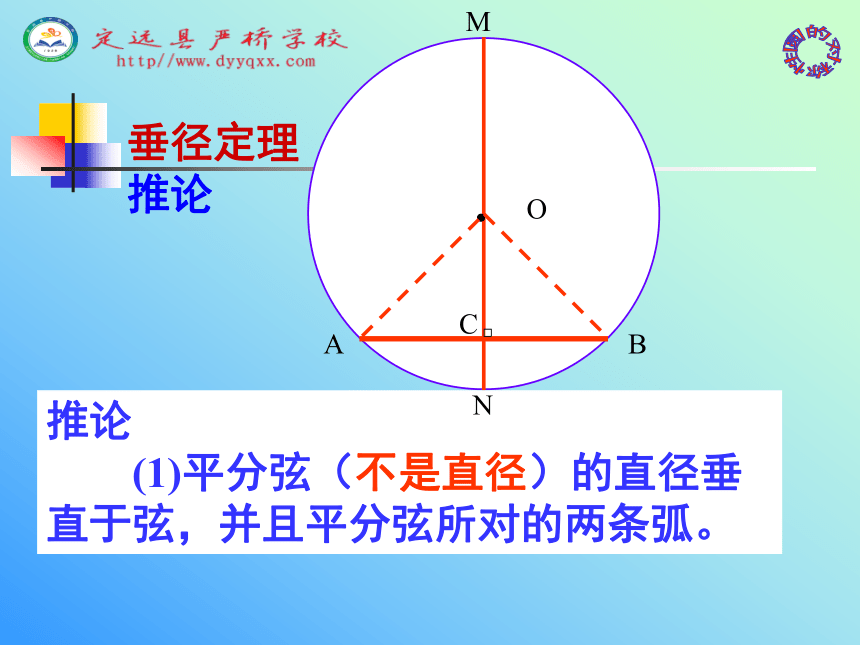
推论 (1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。垂径定理 推论NMOACBN② MN⊥AB ③ AC=BC
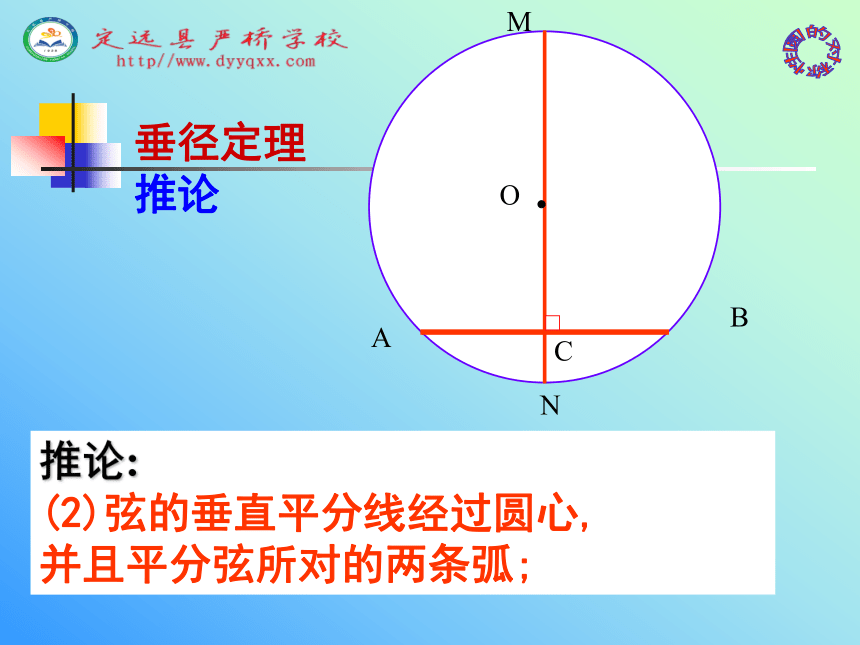
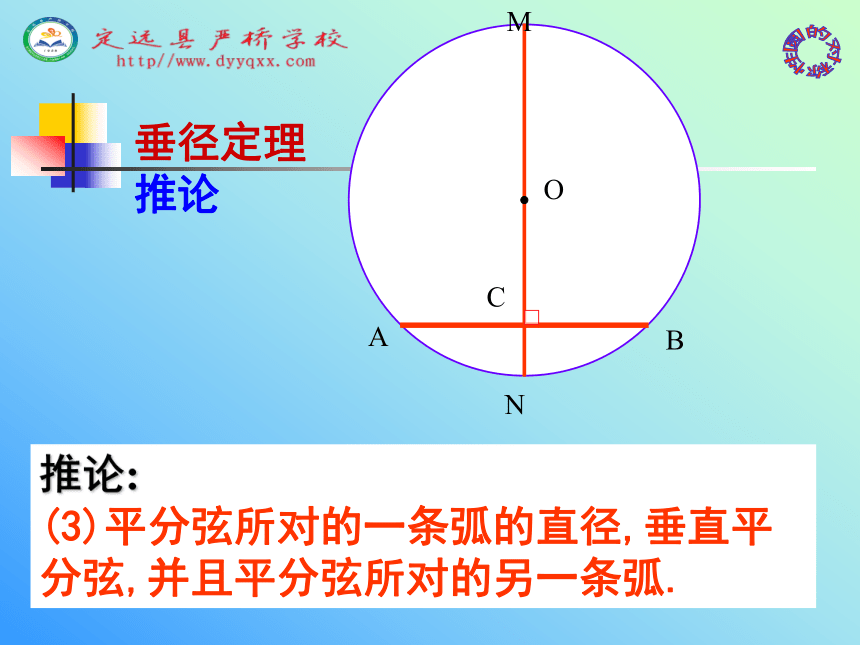
垂径定理 推论推论: (2)弦的垂直平分线经过圆心, 并且平分弦所对的两条弧;MOACBN推论: (3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.垂径定理 推论根据垂径定理与推论可知对于一个圆和一条直线来说。如果具备(1)过圆心 (2)垂直于弦 (3)平分弦 (4)平分弦所对的优弧 (5)平分弦所对的劣弧上述五个条件中的任何两个条件都可以推出其他三个结论垂径定理:
“知二推三”操作探究(1) 在两张透明纸上,分别作半径相等的
⊙O和⊙O′,把两张纸叠在一起,使⊙O和⊙O′重合,用图钉钉住圆心。将上面一个
圆旋转任意一个角度,两个圆还能重合吗?圆是中心对称图形吗?O( O′)圆是旋转对称图形,旋转中心为圆心。 在平面内,一个图形绕某个点旋转180°,如果旋转前后的图形能互相重合,那么这个图形叫做中心对称图形。 判别下列各图中的角是不是圆心角,并说明理由。如图,顶点在圆心的角叫圆心角.操作探究(2)①认识圆心角ABB′A′如:∠AOB、∠A′OB′等OABMB′OM′A′操作探究(2) ②圆心角、弧、弦、弦心距之间的关系当∠AOB=∠A′OB′时,根据圆的性质,
你能推测出两个圆心角所对的弧AB与弧A′B′、弦AB与弦A′B、弦心距OM与弦心距OM′之间有怎样的关系?根据圆的旋转对称性,把∠AOB连同弧AB绕圆心O旋转,使射线OA与OA′重合,设∠A′OA=α ∵ ∠AOB= ∠A′OB′
∴ ∠B′OB = ∠A′OB′+ ∠A′OB
= ∠AOB + ∠A′OB =α
所以射线OB与OB′重合。
又∵OA=OA′OB=OB′,
所以旋转后A与A′重合,B与B′重合。圆心角、弧、弦、弦心距之间的关系(1)定理:在同圆或等圆中,相等的圆心角所对的弦相等,所对的弧相等,所对的弦心距相等。条件:结论:在同圆或等圆中圆心角相等圆心角所对弧相等圆心角所对弦相等圆心角所对的弦心距相等猜想:把圆心角相等与三个结论的任何一个 交换位置,有怎样的结果?(2) 定理:
在同圆或等圆中,如果两个圆心角、两条弧、
两条弦或两条弦的弦心距中有一组量相等,
那么它们所对应的其余各组量都分别相等。
圆心角相等弧相等弦相等弦心距相等“知一推三”在同圆或等圆中: 如图,AB,CD是⊙O的两条弦,
OE、OF为AB、CD的弦心距,ABCFDEO(2)如果OE=OF,那么 , , ;(4)如果AB=CD,那么 , , 。(1)如果∠AOB=∠COD,那么 , , ;∠AOB=∠COD AB=CD OE=OF牛刀小试:
把顶点在圆心的周角等分成360份,每一份的圆心角是1°的角,整个圆周被等分成360份,我们把每一份这样的弧叫做1°的弧。
一般地,n°的圆心角对着n°的弧, n°的弧对着n°的圆心角。
结论:圆心角的度数和它所对的弧的度数相等。
1°的弧:例题讲解:例4:已知:如图,等边三角形ABC的三个顶点都在⊙O上。 求证:∠AOB= ∠ BOC= ∠ COA=120°证明:∵AB=BC=CA
∴ ∠AOB= ∠ BOC = ∠ COA
ABCO·AEFCDOK′K 例5:如图,点O是∠A平分线上的一点,以O为圆心的圆和角的两边分别交于点C、D和E、F 求证:CD=EF证明:作OK′⊥EF,OK⊥CD,K′、K为垂足,∵OK= OK′
(角平分线性质)
∴CD= EF“知一推三”弦相等弦心距相等例6:已知 AB和CD为⊙O的两条直径,弦CE∥AB, 为40°.
求∠BOD的度数。解:连接OE
∵ =40°
∴∠COE =40°
∵OC=OE
∴∠OCE=
又CE∥AB,
∴∠AOD=∠OCE=70°
∴ ∠BOD=180°-70°=110°崭露头角:(不对)(不对)下列说法正确吗?为什么??1、一条弦把圆分成3:6两部分,则优弧所对
的圆心角为 °.
?2、A、B、C为⊙O上三点,若 、 、
的度数之比为1:2:3,
则∠AOB= °,
∠BOC= °, ∠COA= °.
?3、在⊙O中, 的度数为60°, 的长
是圆周长的 。
?锋芒毕露:240601201801、圆具有“旋转不变性”。
即:圆绕圆心旋转任意角度,都能与本身重合
2、圆心角、1°的弧的定义。
3、四个量之间的等量关系。(知一推三)
4、圆心角的度数和它所对的弧的度数的关系。
(相等)
5、常添的辅助线:作出半径、弦心距本节课,你收获了什么?课堂小结:布置作业:课堂作业:
课本习题24.2 第7、8题
家庭作业
必做题:完成习题24.2 剩下的题目。
选做题:
中考链接:(2010年芜湖市中考题)
在⊙O内,有折线OABC,其中OA=8,AB=12,∠A=∠B=60°,则BC的长为
oABC提示:过点O作CD⊥BC,延长AO交BC于E,则△ABE为等边三角形。DE结束寄语 在数学领域中,提出问题的艺术比解答的艺术更为重要.
——康托尔再见
2、理解圆心角的概念.
3、掌握圆心角、弧、弦、弦心距之间的相等关系定理及推论. (知一推三)
4、理解“1°的弧”的概念。学习目标:垂径定理 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.题设结论(1)直径
(2)垂直于弦}{(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧MOACBN①直线MN过圆心②MN⊥AB③ AC=BC
④ ⑤垂径定理MOACBN①直线MN过圆心③ AC=BC
推论 (1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。垂径定理 推论NMOACBN② MN⊥AB ③ AC=BC
垂径定理 推论推论: (2)弦的垂直平分线经过圆心, 并且平分弦所对的两条弧;MOACBN推论: (3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.垂径定理 推论根据垂径定理与推论可知对于一个圆和一条直线来说。如果具备(1)过圆心 (2)垂直于弦 (3)平分弦 (4)平分弦所对的优弧 (5)平分弦所对的劣弧上述五个条件中的任何两个条件都可以推出其他三个结论垂径定理:
“知二推三”操作探究(1) 在两张透明纸上,分别作半径相等的
⊙O和⊙O′,把两张纸叠在一起,使⊙O和⊙O′重合,用图钉钉住圆心。将上面一个
圆旋转任意一个角度,两个圆还能重合吗?圆是中心对称图形吗?O( O′)圆是旋转对称图形,旋转中心为圆心。 在平面内,一个图形绕某个点旋转180°,如果旋转前后的图形能互相重合,那么这个图形叫做中心对称图形。 判别下列各图中的角是不是圆心角,并说明理由。如图,顶点在圆心的角叫圆心角.操作探究(2)①认识圆心角ABB′A′如:∠AOB、∠A′OB′等OABMB′OM′A′操作探究(2) ②圆心角、弧、弦、弦心距之间的关系当∠AOB=∠A′OB′时,根据圆的性质,
你能推测出两个圆心角所对的弧AB与弧A′B′、弦AB与弦A′B、弦心距OM与弦心距OM′之间有怎样的关系?根据圆的旋转对称性,把∠AOB连同弧AB绕圆心O旋转,使射线OA与OA′重合,设∠A′OA=α ∵ ∠AOB= ∠A′OB′
∴ ∠B′OB = ∠A′OB′+ ∠A′OB
= ∠AOB + ∠A′OB =α
所以射线OB与OB′重合。
又∵OA=OA′OB=OB′,
所以旋转后A与A′重合,B与B′重合。圆心角、弧、弦、弦心距之间的关系(1)定理:在同圆或等圆中,相等的圆心角所对的弦相等,所对的弧相等,所对的弦心距相等。条件:结论:在同圆或等圆中圆心角相等圆心角所对弧相等圆心角所对弦相等圆心角所对的弦心距相等猜想:把圆心角相等与三个结论的任何一个 交换位置,有怎样的结果?(2) 定理:
在同圆或等圆中,如果两个圆心角、两条弧、
两条弦或两条弦的弦心距中有一组量相等,
那么它们所对应的其余各组量都分别相等。
圆心角相等弧相等弦相等弦心距相等“知一推三”在同圆或等圆中: 如图,AB,CD是⊙O的两条弦,
OE、OF为AB、CD的弦心距,ABCFDEO(2)如果OE=OF,那么 , , ;(4)如果AB=CD,那么 , , 。(1)如果∠AOB=∠COD,那么 , , ;∠AOB=∠COD AB=CD OE=OF牛刀小试:
把顶点在圆心的周角等分成360份,每一份的圆心角是1°的角,整个圆周被等分成360份,我们把每一份这样的弧叫做1°的弧。
一般地,n°的圆心角对着n°的弧, n°的弧对着n°的圆心角。
结论:圆心角的度数和它所对的弧的度数相等。
1°的弧:例题讲解:例4:已知:如图,等边三角形ABC的三个顶点都在⊙O上。 求证:∠AOB= ∠ BOC= ∠ COA=120°证明:∵AB=BC=CA
∴ ∠AOB= ∠ BOC = ∠ COA
ABCO·AEFCDOK′K 例5:如图,点O是∠A平分线上的一点,以O为圆心的圆和角的两边分别交于点C、D和E、F 求证:CD=EF证明:作OK′⊥EF,OK⊥CD,K′、K为垂足,∵OK= OK′
(角平分线性质)
∴CD= EF“知一推三”弦相等弦心距相等例6:已知 AB和CD为⊙O的两条直径,弦CE∥AB, 为40°.
求∠BOD的度数。解:连接OE
∵ =40°
∴∠COE =40°
∵OC=OE
∴∠OCE=
又CE∥AB,
∴∠AOD=∠OCE=70°
∴ ∠BOD=180°-70°=110°崭露头角:(不对)(不对)下列说法正确吗?为什么??1、一条弦把圆分成3:6两部分,则优弧所对
的圆心角为 °.
?2、A、B、C为⊙O上三点,若 、 、
的度数之比为1:2:3,
则∠AOB= °,
∠BOC= °, ∠COA= °.
?3、在⊙O中, 的度数为60°, 的长
是圆周长的 。
?锋芒毕露:240601201801、圆具有“旋转不变性”。
即:圆绕圆心旋转任意角度,都能与本身重合
2、圆心角、1°的弧的定义。
3、四个量之间的等量关系。(知一推三)
4、圆心角的度数和它所对的弧的度数的关系。
(相等)
5、常添的辅助线:作出半径、弦心距本节课,你收获了什么?课堂小结:布置作业:课堂作业:
课本习题24.2 第7、8题
家庭作业
必做题:完成习题24.2 剩下的题目。
选做题:
中考链接:(2010年芜湖市中考题)
在⊙O内,有折线OABC,其中OA=8,AB=12,∠A=∠B=60°,则BC的长为
oABC提示:过点O作CD⊥BC,延长AO交BC于E,则△ABE为等边三角形。DE结束寄语 在数学领域中,提出问题的艺术比解答的艺术更为重要.
——康托尔再见
