沪科版初中数学九下24.7弧长与扇形面积(共14张PPT)
文档属性
| 名称 | 沪科版初中数学九下24.7弧长与扇形面积(共14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 547.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-26 07:50:41 | ||
图片预览





文档简介
课件14张PPT。§24.7弧长与扇形面积问题2.在学校运动会二百米跑比赛中,每位运动员的起跑位置相同吗?每位运动员弯道的展直长度相同吗?问题1.半径为R圆的周长与面积分别是多少? 学法指导 认真阅读课本53-55页有关内容,完成下列自学任务:
1、什么样的图形叫扇形?
2、 1°的圆心角所对弧长等于圆周长的 , 所对扇形面积等于圆面积的 ,n° 圆心角所对的弧长和扇形面积都是 1°的圆心角所对的弧长和扇形面积的 倍;由此猜想怎样求扇形的弧长和面积。
3.考古发现一破残古铜镜弧长1 8.2cm,
其所对圆心角为14.4 ° ,若想“破镜重圆”
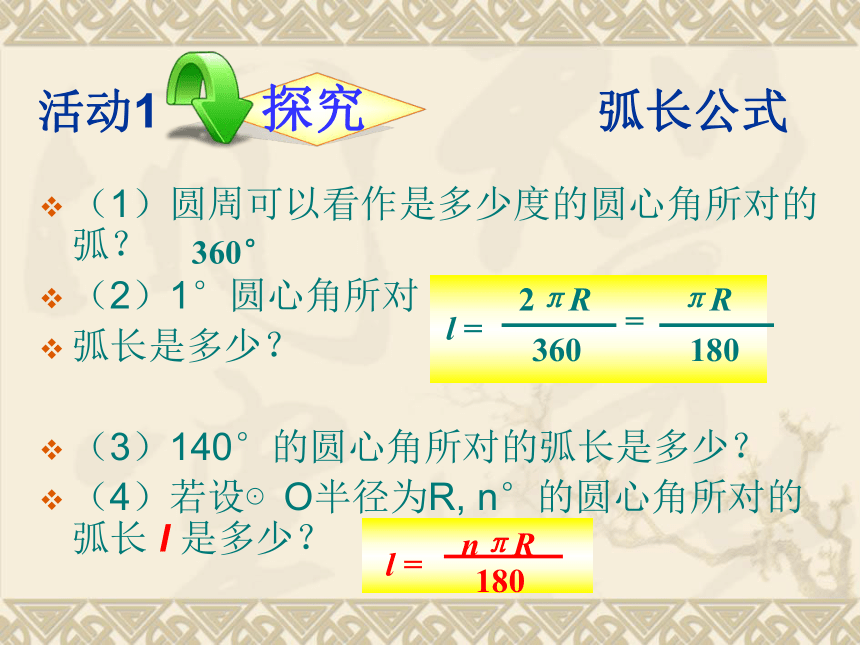
求复原后的铜镜周长。(1)圆周可以看作是多少度的圆心角所对的弧?
(2)1°圆心角所对
弧长是多少?
(3)140°的圆心角所对的弧长是多少?
(4)若设⊙O半径为R, n°的圆心角所对的弧长 l 是多少?活动1 弧长公式360°(1)在弧长公式中, n 表示1°的圆心角的倍数, n 和180都不带单位.
(2)要正确区分弧、弧的度数、弧长三个概念.任何一段弧都有长度和度数,故度数相等的弧、弧长不一定相等;弧长相等的弧也不一定是等弧.等弧的度数和长度一定分别相等.
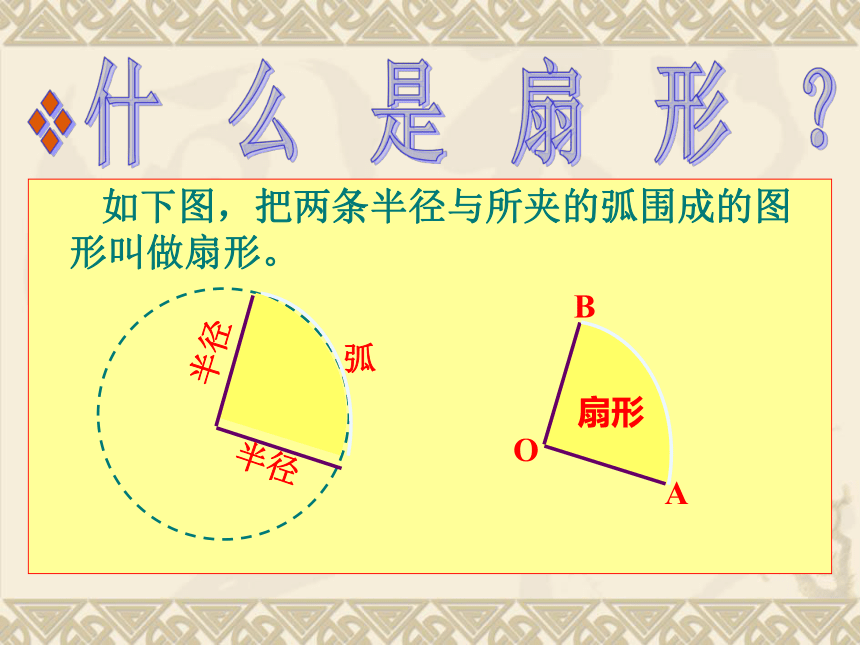
(3)公式中出现的三个量、n、R中,只要知道其中两个,就能求出第三个.举一反三什 么 是 扇 形 ? 如下图,把两条半径与所夹的弧围成的图形叫做扇形。活动2 探索扇形面积公式(1)圆面可以看作是多少度的圆心角所对的扇形?
(2)1°圆心角所对
扇形面积是多少?
(3)若设⊙O半径为R, n°的圆心角所对的扇形面积S怎样表示?
360° 归纳∴∵比较扇形面积与弧长公式,用弧长表示扇形面积:公式中出现的三个量,l,R,S或S,R,n中,已知其中两个量即可求出第三个量.除了应用扇形的面积公式计算扇形的面积及弓形的面积外,也要善于把公式变形,利用它求圆心角和半径R.举一反三如:已知扇形面积为 ,圆心角为60°,
则这个扇形的半径R=____. 例1 一滑轮起重装置如图26-60,
滑轮的半径R=10cm,当重物上升
15.7cm时,问滑轮的一条半径OA
绕轴心O按逆时针方向旋转的角
度?(假设绳索与滑轮之间没有
滑动,取3.14)例2、古希腊埃拉托塞尼曾给出一个估算地球周长(或整个子午圈长)的简单方法,如图。点S和点A分别表示埃及的塞伊尼和亚历山大两地,亚历山大在塞伊尼的北方,两地经度大致相同,两地的实际距离为5000希腊里(1希腊里≈158.5m),当太阳光线在塞伊尼直射时,同一时刻在亚历山大测量太阳光线偏离直射方向的角为α,他实际测得α是7.2°,由此估算出了地球的周长,
你能进行计算吗?背景链接埃拉托塞尼生活在亚历山大城,在这座城市正南785千米处,有一座和亚历山大城同在一
条子午线(30°E)上的城市
塞伊尼。夏至日正午12点,阳光
直射塞尼城中一口枯井底部的
同时,埃拉托塞尼在亚历山大
城使用木竿和量角器精确计算
出了地球的周长(图中角1为7.2°)。小 结 (1)弧长和扇形面积公式是什么?你是如何得到这两个公式的?如何运用?(2)弧长与圆周长、扇形面积与圆面积之间有什么联系?
(3)埃拉托塞尼估算地球周长的故事对你
有什么启发?P57习题24.7
2.3.5独立完成作业的良好习惯,
是成长过程中的良师益友。
1、什么样的图形叫扇形?
2、 1°的圆心角所对弧长等于圆周长的 , 所对扇形面积等于圆面积的 ,n° 圆心角所对的弧长和扇形面积都是 1°的圆心角所对的弧长和扇形面积的 倍;由此猜想怎样求扇形的弧长和面积。
3.考古发现一破残古铜镜弧长1 8.2cm,
其所对圆心角为14.4 ° ,若想“破镜重圆”
求复原后的铜镜周长。(1)圆周可以看作是多少度的圆心角所对的弧?
(2)1°圆心角所对
弧长是多少?
(3)140°的圆心角所对的弧长是多少?
(4)若设⊙O半径为R, n°的圆心角所对的弧长 l 是多少?活动1 弧长公式360°(1)在弧长公式中, n 表示1°的圆心角的倍数, n 和180都不带单位.
(2)要正确区分弧、弧的度数、弧长三个概念.任何一段弧都有长度和度数,故度数相等的弧、弧长不一定相等;弧长相等的弧也不一定是等弧.等弧的度数和长度一定分别相等.
(3)公式中出现的三个量、n、R中,只要知道其中两个,就能求出第三个.举一反三什 么 是 扇 形 ? 如下图,把两条半径与所夹的弧围成的图形叫做扇形。活动2 探索扇形面积公式(1)圆面可以看作是多少度的圆心角所对的扇形?
(2)1°圆心角所对
扇形面积是多少?
(3)若设⊙O半径为R, n°的圆心角所对的扇形面积S怎样表示?
360° 归纳∴∵比较扇形面积与弧长公式,用弧长表示扇形面积:公式中出现的三个量,l,R,S或S,R,n中,已知其中两个量即可求出第三个量.除了应用扇形的面积公式计算扇形的面积及弓形的面积外,也要善于把公式变形,利用它求圆心角和半径R.举一反三如:已知扇形面积为 ,圆心角为60°,
则这个扇形的半径R=____. 例1 一滑轮起重装置如图26-60,
滑轮的半径R=10cm,当重物上升
15.7cm时,问滑轮的一条半径OA
绕轴心O按逆时针方向旋转的角
度?(假设绳索与滑轮之间没有
滑动,取3.14)例2、古希腊埃拉托塞尼曾给出一个估算地球周长(或整个子午圈长)的简单方法,如图。点S和点A分别表示埃及的塞伊尼和亚历山大两地,亚历山大在塞伊尼的北方,两地经度大致相同,两地的实际距离为5000希腊里(1希腊里≈158.5m),当太阳光线在塞伊尼直射时,同一时刻在亚历山大测量太阳光线偏离直射方向的角为α,他实际测得α是7.2°,由此估算出了地球的周长,
你能进行计算吗?背景链接埃拉托塞尼生活在亚历山大城,在这座城市正南785千米处,有一座和亚历山大城同在一
条子午线(30°E)上的城市
塞伊尼。夏至日正午12点,阳光
直射塞尼城中一口枯井底部的
同时,埃拉托塞尼在亚历山大
城使用木竿和量角器精确计算
出了地球的周长(图中角1为7.2°)。小 结 (1)弧长和扇形面积公式是什么?你是如何得到这两个公式的?如何运用?(2)弧长与圆周长、扇形面积与圆面积之间有什么联系?
(3)埃拉托塞尼估算地球周长的故事对你
有什么启发?P57习题24.7
2.3.5独立完成作业的良好习惯,
是成长过程中的良师益友。
