6.4 密度的应用 学案(有答案)
图片预览




文档简介
/ 让教学更有效 高效备课 | 物理学科
【学习目标】
1. 会用密度公式来求质量
2. 会用密度公式来求体积
3. 能鉴别物质是否为纯的(区分空心、合金)
4. 能通过密度公式来求冰块融化问题
5. 能通过密度公式解决冰块中包其它物体的问题
【自主学习】
一、利用密度求出质量
知道了物体的体积(这里需要单独利用数学公式或者几何关系求出物体的体积),查出组成物质的密度,就可以算出物体的 。对于不易直接称量质量的庞大物体,这种办法很方便。
二、利用密度求出体积
知道了物体的质量,查出组成物质的密度,就可以算出物体的 。对于形状不规则或不便于直接测量体积的物体,这是一种很方便的求体积的办法。
三、利用密度鉴别物质
如果测出由某种物质组成的物体的密度,再把测得的密度跟密度表中各种物质的密度比较一下,就可以知道该物体 是由什么物质构成的了。
不同物质的密度可能是相同的。例如,酒精和煤油都是液体,它们的密度都是0.8×103kg/m3,但是通过 可以区分它们。因此,要准确地鉴别物质,常常需要多种方法并用。
【例1】有质量相等的两个球,它们的体积之比为V1∶V2=1∶6,材料的密度之比为ρ1∶ρ2=4∶1,其中有一个是空心的,已知实心球的体积是V,则空心球的空心部分的体积与实心球的体积之比是( )
A.2∶1
B.1∶2
C.3∶4
D.4∶3
【例2】铝的密度是木头的5倍,质量相同的铝块和木块,它们的体积之比为1:4,则下列说法正确的是( )
A.木块一定是空心的
B.铝块和木块一定都是空心的
C.若木块是实心的,铝块空心部分的体积占其总体积的五分之一
D.若木块是实心的,铝块空心部分的体积占其总体积的四分之一
【例3】有一个体积为60cm3的空心铁球,质量为395g,在铁球的空心部分注满某种液体后总质量为407g,ρ铁=7.9×103kg/m3,ρ水=1.0×103kg/m3,下列说法中正确的是( )
A.空心部分的体积40cm3
B.注入液体后该球的平均密度为5.15kg/m3
C.这种液体的密度1.2kg/m3
D.若空心部分注满水,其总质量为405g
【例4】如图所示,某冰块夹杂着一个石块,沉没在柱形容器的水底。其中冰的质量是45g,石块的质量是12g,冰块的总体积是56cm3,容器的底面积为10cm2,水的密度为,冰的密度为,求:
(1)冰块中冰的体积是多少cm3?
(2)石块的密度是多少g/cm3?
(3)若冰全部熔化成水,容器中的水面下降多少cm?
【例5】甲物质的密度为5g/cm3,乙物质密度为2g/cm3,各取一定体积混合均匀后密度为3g/cm3,假设混合前后总体积保持不变,则所取甲、乙两种物质的体积之比是( )
A.5:2 B.2:5
C.1:2 D.2:1
【例6】新冠疫情期间,医疗物资紧缺,小杜利用简单道具在家配制75度(1度是指100mL的酒液中含有酒精的体积为1mL消毒酒液)。现有一个底面积为100cm2的足够高圆柱形容器,容器中装有10cm高的90度酒液,此时酒液的质量为 g;为了配制75度酒液,小杜将水缓慢加入其中(不考虑混合后体积的变化),则小杜最多可以配制75度酒液 g(已知酒精密度为0.8g/cm3)。
【例7】文文同学对合金制成的机器零件进行探究。她用天平测出一个合金构件的质量为748g,用量杯测出该构件的体积是200cm3,她查阅了该构件说明书,得知该合金构件由铝与钢两种材料合成,钢的体积占比为20%,且铝的密度为2.7×103kg/m3,如果构件的体积等于两种金属体积之和。求:
(1)该合金材料的平均密度是多少kg/m3?
(2)该合金构件中钢的密度是多少kg/m3?
(3)若用该合金材料去替换机器的某一钢制零件,质量比钢制零件减少了832g,求该钢制零件的质量是多少g?
【例8】“玫瑰金”是一种黄金和铜的合金。小庆想买一件如图所示的玫瑰金工艺品送给他的朋友,商店的售货员告诉他们,这件合金工艺品是由金和铜两种金属混合而成的,其含金量为80%(金的质量占金和铜总质量的百分比)。小庆朋友对商店售货员的话表示怀疑,于是便让小庆进行验证。小庆利用所学的物理知识测出了这件工艺品的质量为900g,体积为(为方便计算,假设,)。则下列说法正确的是( )
A.按商店售货员的说法,这件工艺品的体积为
B.根据小庆的实验数据,这件工艺品的密度是
C.按商店售货员的说法,这件工艺品的密度是
D.根据小庆的实验数据,这件工艺品的含金量是70%
【课后巩固】
1.一枚实心纪念币的质量为16g,体积为2cm3,纪念币的密度是 kg/m3,可见,这枚纪念币 (填“是”或“不是”)纯金制。(ρ金=19.3×103kg/m3)
2.小明到市场上购买了2斤蜂蜜,回家用电子秤测质量,果真是2斤。小明想这个蜂蜜肯定没掺水,是纯正的好蜂蜜。你认为小明用测量质量 办法判断蜂蜜是否掺水是 (选填“合理”或“不合理”)的,你的理由是 。
3.利用质量相同的铜和铝,制成体积相等的两个球(ρ铜>ρ铝)。则下列判断正确的是( )
A.铝球一定是空心的
B.铜球一定是空心的
C.铝球一定是实心的
D.若两球都是空心的,则铝球的空心部分体积大
4.a、b是两个由同种材料制成的金属球,它们的质量分别为60g和128g,体积分别为和。在这两个金属球中,如果有一个是实心的,那么( )
A.a是实心球,金属密度是 B.a是实心球,金属密度是
C.b是实心球,金属密度是 D.b是实心球,金属密度是
5.用质量相同的铁、铜、铅制成体积相同的金属球,可能出现的情况是( )(铅、铜、铁密度依次减小)
①如果铜球是实心的,那么铁球一定是空心的
②如果铁球是空心的,那么铜球、铅球一定是空心的
③如果铅球是实心的,则铁球、铜球可能是空心的
④三个球若都是空心的,则空心部分的体积一定是V铅>V铜>V铁
A.①③ B.②④ C.④ D.①④
6.有a、b两个小球分别由、的甲、乙两种材料制成,两小球质量分别为30g和25g,体积之比为,则下列说法正确的是( )
A.若只有一个球是空心,则a球是空心的
B.若只有一个球是空心,则空心球的空心部分与实心部分体积之比为1:4
C.若两球均是空心的,a球的空心部分体积可以比b球的空心部分体积大
D.若只有一个球是空心,将空心球的空心部分装满水后,两球总质量相等
7.下列关于密度说法中正确的是( )
A.水和冰是同种物质,所以它们的密度相同
B.可以利用密度来鉴别物质,因为不同物质的密度一定不同
C.为减轻质量,航空器材常采用强度高、密度大的合金或新型合成材料
D.火灾时,受困人员弯腰撤离,原因是燃烧产生的有害气体温度较高,密度较小
8.用质量均为1kg的水和甲液体(甲液体的密度为0.8×103kg/m3)配制密度为0.9×103kg/m3的乙液体。则最多能配成乙液体 kg。
9.农业上常采用配制适当密度的盐水进行选种。在选稻种时需用密度是1.1×103kg/m3的盐水,现配制了500cm3的盐水,称得它的质量为505g,这样的盐水 (符合/不符合)要求,如不符合要求,应加 (盐/水) g。(ρ食盐=2.2×103kg/m3,不考虑混合后体积的变化)
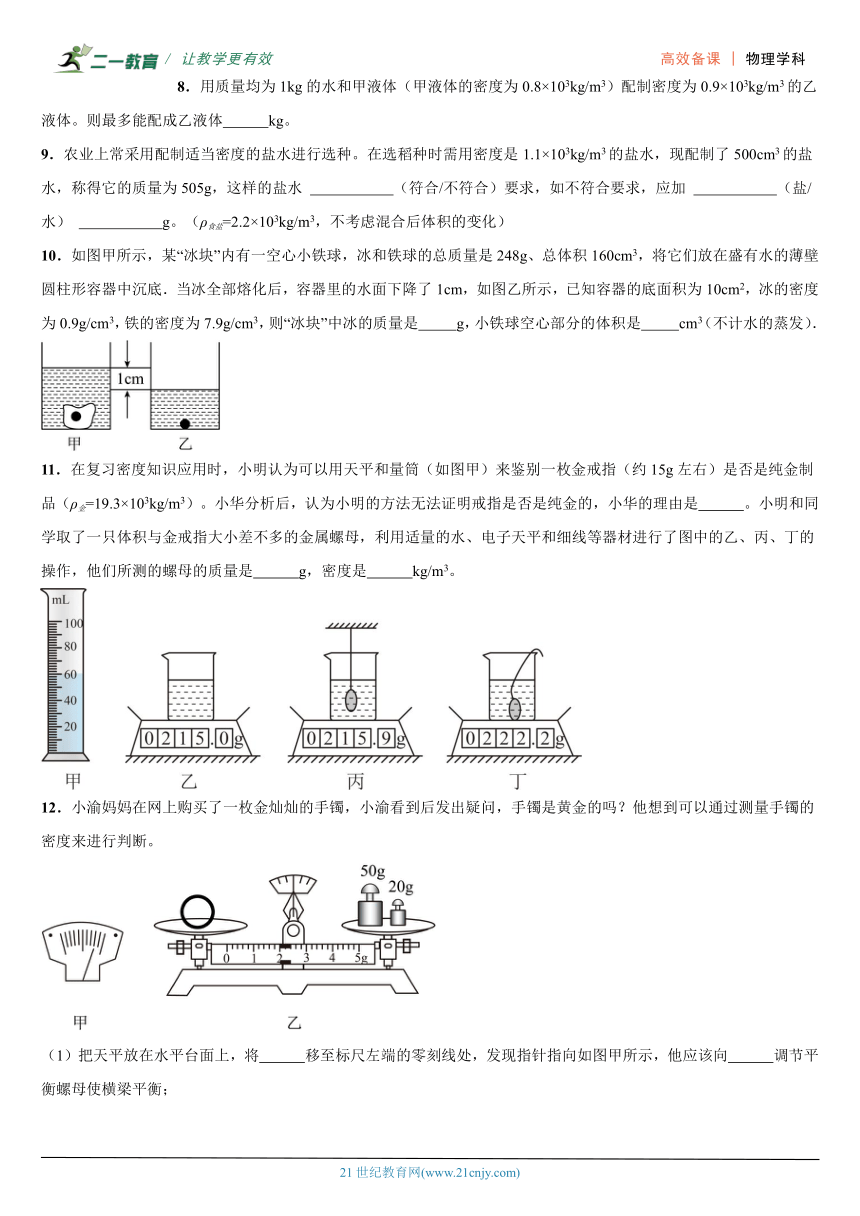
10.如图甲所示,某“冰块”内有一空心小铁球,冰和铁球的总质量是248g、总体积160cm3,将它们放在盛有水的薄壁圆柱形容器中沉底.当冰全部熔化后,容器里的水面下降了1cm,如图乙所示,已知容器的底面积为10cm2,冰的密度为0.9g/cm3,铁的密度为7.9g/cm3,则“冰块”中冰的质量是 g,小铁球空心部分的体积是 cm3(不计水的蒸发).
11.在复习密度知识应用时,小明认为可以用天平和量筒(如图甲)来鉴别一枚金戒指(约15g左右)是否是纯金制品(ρ金=19.3×103kg/m3)。小华分析后,认为小明的方法无法证明戒指是否是纯金的,小华的理由是 。小明和同学取了一只体积与金戒指大小差不多的金属螺母,利用适量的水、电子天平和细线等器材进行了图中的乙、丙、丁的操作,他们所测的螺母的质量是 g,密度是 kg/m3。
12.小渝妈妈在网上购买了一枚金灿灿的手镯,小渝看到后发出疑问,手镯是黄金的吗?他想到可以通过测量手镯的密度来进行判断。
(1)把天平放在水平台面上,将 移至标尺左端的零刻线处,发现指针指向如图甲所示,他应该向 调节平衡螺母使横梁平衡;
(2)测量手镯质量时,右盘中的砝码和游码的位置如图乙所示,手镯的质量为 g;
(3)手镯太大不能直接用量筒和水测体积,小渝经过思考进行了如下的实验操作:
①将适量水倒入烧杯内,并置于天平上,调节平衡后天平示数为100g;
②用细线系好手镯缓慢浸没到水中保持静止,手镯始终未与烧杯接触,调节平衡后天平示数为109g;
根据测得的数据可以计算出该手镯的密度ρ= kg/m3;若实验中忘了进行第①步测量,取出手镯后才测量烧杯和水的质量,则所计算出的密度比真实值 (选填“偏大”、“偏小”或“不变”);
(4)结合表格二,若该手镯为实心则 (选填“是”或“不是”)纯金的。通过网上查找资料得知,这种金色手镯大多是铜锌合金制成,若妈妈的手镯也是铜锌合金且为实心,则其中含有铜和锌的质量之比为 ;
表二
物质 铝 锌 铁 铜 银 金
密度g/cm3 2.7 7.1 7.9 8.9 10.5 19.3
(5)跟商家投诉后,商家辩称手镯为空心,所以密度才比纯金小,根据你所学到的各学科知识,为进一步验证手镯是否为纯金,请写出你的方法: 。
13.小丽妈妈过年时送给小丽一件纯金挂件“福兔”,小丽想知道这个挂件是实心还是空心,于是她利用天平、量筒进行测量,她的操作如下:
(1)她把天平放在 上,游码拨到零刻度线,发现指针位置如图甲所示,她接下来的第一步操作应该是将平衡螺母向 调(选填“左”或“右”);
(2)她用调好的天平称挂件的质量如图乙,则挂件的质量为 g;
(3)将挂件放入量筒并倒入适量水,如图丙所示。取出挂件,量筒中剩余水的体积为30mL,挂件的体积为 cm3,密度为 g/cm3;
(4)小丽翻书查阅纯金的密度是19.3g/cm3,请你帮助小丽判断一下此挂件是不是实心的,如果是空心的,则空心的体积有多大 。(写出必要的文字说明、表达式及最后结果)
14.小明有一个质量为158g、体积为30cm3的空心铁球。若将该空心铁球压扁,并与一定量的铝混合浇铸形成了一个铁铝合金块,将这个合金块放入一个装满水的容器中,溢出50g水。(已知ρ铁=7.9×103kg/m3,ρ铝=2.7×103kg/m3,ρ冰=0.9×103kg/m3)。求:
(1)铁球空心部分的体积;
(2)将铁球的空心部分充满冰后的总质量;
(3)浇铸的铁铝合金块的平均密度。
15.周末小明去商店购买了一个小铁球,为了判断小铁球是实心还是空心的,小明找来一个质量为100g的空瓶子,装满水后瓶子的总质量为600g。如果把小铁球装进空瓶子中,测得瓶子的总质量为900g,然后在瓶子中装满水,测得瓶子、水和小铁球的总质量为1200g,ρ铁=7.9×103kg/m3,ρ水=1.0×103kg/m3,求:
(1)小铁球的质量;
(2)瓶子的容积;
(3)小铁球的体积;
(4)请你通过计算并判断小球是空心的还是实心的?
16.某种子公司为选种,需要配制密度为的盐水。工作人员先在量筒内放入一定量的纯水,如图甲所示,再加24g盐完全溶解在的量筒内的水中,液面升高后的位置如图乙所示。求:
(1)乙量筒内盐水的质量;
(2)计算说明配制的盐水密度是否符合要求?
(3)若不符合要求需要加水还是加盐,加多少克的水或盐?
1.我国科学家研发的固体浮力材料已成功用于万米深海探测,为深潜器提供浮力,技术水平居于世界前列,固体浮力材料的核心是“微球”(直径很小的空心玻璃球)。若用质量为60g,密度为2.4g/cm3的玻璃制成“微球”后和粘合剂黏合制成一块固体浮力材料,其内部结构的放大示意图如图所示。粘剂的密度为1.2g/cm3,粘合剂体积占固体浮力材料总体积的20%,制成后的固体浮力材料密度为0.48g/cm3。下列说法错误的是( )
A.这块固体浮力材料中所用玻璃的体积是25cm3
B.这块固体浮力材料的总体积是250cm3
C.这块固体浮力材料中粘合剂的质量为60g
D.这块固体浮力材料中空心部分的体积为200cm3
2.西贝同学测量密度时,先用天平测得装满水的溢水杯质量为500g,将一空心金属块缓慢浸没在溢水杯中,稳定后,用天平测得溢水杯的总质量为750g,然后将金属块从溢水杯中取出(假设取出时不带水),再次测得溢水杯的总质量为440g,若将空心部分填满酒精,则金属球的质量变为326g,则空心部分的体积为 cm3,该金属材料的密度为 kg/m3。(已知ρ酒精=0.8g/cm3)
3.白酒的主要成分是水和酒精。目前中国使用白酒的度数表示法称为标准酒度,是指在温度为20℃的条件下,每100mL白酒中所含酒精的毫升数,酒厂为得到相应的酒度,需将高度白酒与低度白酒进行勾兑(混合)。现有60度高度白酒和20度低度白酒若干(已知ρ酒精=0.8×103kg/m3,ρ水=1.0×103kg/m3,不考虑白酒混合前后体积变化),则100mL的60度白酒中所含酒精体积是 mL,60度白酒的平均密度是 g/cm3;20度白酒密度 (大于/等于/小于)60度白酒密度;如果用60度和20度这两种白酒进行勾兑,获得1000mL 52度的白酒,那么所用60度白酒的质量是 kg。
4.如图所示,两个完全相同的圆柱形容器A与B,它们的底面积为,高8cm,放在水平桌面上。已知A容器装有5.2cm深的水,B容器装有2.8cm深的盐水,盐水质量为340g。现将一块体积为的铁块浸没在B容器的盐水中,B容器中有盐水溢出,将溢出的盐水完全收集后倒入A容器,再将一块总质量为240g的夹杂有小石块的不规则冰块完全浸没于A中,此时冰未熔化,A容器液面恰好与杯口相平。经过很长一段时间,冰块熔化,石块沉底,相比于冰熔化前水面下降0.1cm。(不考虑盐水与水混合后体积的变化,,ρ冰=0.9g/cm3)求:
(1)A容器中水的质量为多少g?
(2)该“冰包石”的平均密度为多少?
(3)现将B中剩余盐水倒入A中,整个过程中液体不能溢出,则A中新溶液密度最大为多少?
5.如图所示,桌面上有一质量100g、高8cm、底面积的薄壁柱形容器,容器内装有5cm深的某混合液体200g。将一个金属实心圆柱体慢慢放入容器与底部接触,溢出部分液体,且圆柱体有一半露出液面。此时容器、容器内液体、圆柱体的总质量为1570g,慢慢取出圆柱体后,容器与容器内液体总质量为220g,忽略取出圆柱体时带出的液体。
(1)求混合液体的密度;
(2)求金属块的密度;
(3)若原容器中的混合液体是由水与密度为的液体X配制而来,且水的体积分数(水的体积占混合液总体积的百分比)需控制在40%至60%的范围内,求液体X的密度的取值范围(已知水的密度为),不考虑分子间隙等次要因素,最终结果保留一位小数)。
6.如图所示,底面积为3×10-2m2、高为0.12m的薄壁柱形容器甲和边长为0.1m的实心均匀正方体乙放在水平地面上,甲容器内盛有0.1m深的水。ρ乙=6.75×103kg/m3,ρ水=1.0×103kg/m3。
(1)求甲容器内水的质量;
(2)将实心均匀正方体乙浸没在甲容器的水中(乙不吸水),求溢出水的体积;
(3)若沿正方体乙的上表面向内部挖去一底面积为0.006m2、高为h的长方体丙,并在乙中加满水,是否有可能使加满水后乙的质量与长方体丙的质量相等?若有可能,算出h的值,若不可能,请通过计算说明原因。
7.阅读短文,回答问题
盖 吕萨克酒度
目前国际上白酒的度数表示法有三种,其中一种称为标准酒度,是指在通常条件下,每100毫升白酒中所含酒精量的毫升数,即白酒中酒精和白酒的体积百分比。中国也使用这种表示法,它是法国著名化学家盖 吕萨克制定的,又称盖 吕萨克酒度。
通常白酒的制作流程是将发酵出的低度数的酒液利用如图甲所示的装置蒸馏成高度数的酒液,再根据需要与水或低度酒进行勾兑。勾兑一方面为了保障酒的品质,另一方面可以调整酒的度数。勾兑好的就要密封保存,一旦打开酒瓶瓶盖,会闻到酒精的气味,瓶盖开启时间越长,就越会影响酒的酒度和密度。
说明:已知ρ酒精=0.8×103kg/m3,以下解题过程中,酒液中的微量元素和酒液混合后总体积的微小变化等因素均忽略不计。
(1)如图乙所示,是物质三种状态下的物理模型,与蒸馏过程中酒分子实际变化情况相对应的顺序是 ;
A.ab B.bca C.bab D.cb
(2)将一烧杯白酒放置一段时间,考虑到酒中水和酒精都会挥发,且酒精挥发更快,则可推断杯中剩余酒的标准酒度会 ,密度会 ,(均选填“变大”、“不变”或“变小”);
(3)测得某次蒸馏后接受罐中酒液的密度为0.88×103kg/m3,则该次酒液的标准酒度为 %。如果要将该酒液的度数勾兑成50%,则应往该酒液中加 (选填“水”或“酒精”);
(4)若现用30%和60%的酒液进行勾兑,要获得42%的白酒1000mL。则需要30%的酒液 mL,
,需要60%的酒液 g。
【课后评价】
这节课我给自己☆☆☆☆☆颗星。
【参考答案】
自主学习
一、利用密度求出质量:质量
二、利用密度求出体积:体积
三、利用密度鉴别物质:可能、气味
【例1】A 【例2】C 【例3】D 【例4】(1)50cm3;(2)2g/cm3;(3)0.5cm
【例5】C 【例6】800、1020 【例7】(1)3.74g/cm3;(2)7.9×103kg/m3;(3)1580g
【例8】A
课后巩固
基础练习
1. 8×103、不是 2. 不合理、应该测量密度判断蜂蜜是否掺水 3. B 4. C 5. B 6. D 7. D
8. 1.8 9. 不符合、 盐、90 10. 90、 40
11. 金戒指的体积小于量筒的分度值、7.2、8×103
12. (1)游码、左;(2)72;(3)、偏小;(4)不是 、89︰71;(5)金手镯也可以通过测硬度来鉴别,金手镯的成色越高,质地会越柔软,硬度会越小,很容易被折弯。而成色差的金手镯硬度会比较大,不容易被折弯。(熔化它也行)
13. (1)水平台、左;(2)77.2 ;(3)6、12.9 ;(4)空心,空心的体积为2cm3
14. (1);(2);(3)
15. (1)800g ;(2);(3)200cm3;(4)空心
16. (1)84g;(2)不符合要求;(3)加水,加水70g
能力提升
1. D
2. 20 、
3. 60、0.88、大于、0.704
4. (1)520g;(2);(3)
5. (1)0.8g/cm3;(2)1.6875 g/cm3;(3)0. 5~0.7g/cm3
6. (1)3kg;(2)4×10-4m3;(3)0.09m
7. (1)C; (2)变小、变大;(3)60、水;(4)600、352
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【学习目标】
1. 会用密度公式来求质量
2. 会用密度公式来求体积
3. 能鉴别物质是否为纯的(区分空心、合金)
4. 能通过密度公式来求冰块融化问题
5. 能通过密度公式解决冰块中包其它物体的问题
【自主学习】
一、利用密度求出质量
知道了物体的体积(这里需要单独利用数学公式或者几何关系求出物体的体积),查出组成物质的密度,就可以算出物体的 。对于不易直接称量质量的庞大物体,这种办法很方便。
二、利用密度求出体积
知道了物体的质量,查出组成物质的密度,就可以算出物体的 。对于形状不规则或不便于直接测量体积的物体,这是一种很方便的求体积的办法。
三、利用密度鉴别物质
如果测出由某种物质组成的物体的密度,再把测得的密度跟密度表中各种物质的密度比较一下,就可以知道该物体 是由什么物质构成的了。
不同物质的密度可能是相同的。例如,酒精和煤油都是液体,它们的密度都是0.8×103kg/m3,但是通过 可以区分它们。因此,要准确地鉴别物质,常常需要多种方法并用。
【例1】有质量相等的两个球,它们的体积之比为V1∶V2=1∶6,材料的密度之比为ρ1∶ρ2=4∶1,其中有一个是空心的,已知实心球的体积是V,则空心球的空心部分的体积与实心球的体积之比是( )
A.2∶1
B.1∶2
C.3∶4
D.4∶3
【例2】铝的密度是木头的5倍,质量相同的铝块和木块,它们的体积之比为1:4,则下列说法正确的是( )
A.木块一定是空心的
B.铝块和木块一定都是空心的
C.若木块是实心的,铝块空心部分的体积占其总体积的五分之一
D.若木块是实心的,铝块空心部分的体积占其总体积的四分之一
【例3】有一个体积为60cm3的空心铁球,质量为395g,在铁球的空心部分注满某种液体后总质量为407g,ρ铁=7.9×103kg/m3,ρ水=1.0×103kg/m3,下列说法中正确的是( )
A.空心部分的体积40cm3
B.注入液体后该球的平均密度为5.15kg/m3
C.这种液体的密度1.2kg/m3
D.若空心部分注满水,其总质量为405g
【例4】如图所示,某冰块夹杂着一个石块,沉没在柱形容器的水底。其中冰的质量是45g,石块的质量是12g,冰块的总体积是56cm3,容器的底面积为10cm2,水的密度为,冰的密度为,求:
(1)冰块中冰的体积是多少cm3?
(2)石块的密度是多少g/cm3?
(3)若冰全部熔化成水,容器中的水面下降多少cm?
【例5】甲物质的密度为5g/cm3,乙物质密度为2g/cm3,各取一定体积混合均匀后密度为3g/cm3,假设混合前后总体积保持不变,则所取甲、乙两种物质的体积之比是( )
A.5:2 B.2:5
C.1:2 D.2:1
【例6】新冠疫情期间,医疗物资紧缺,小杜利用简单道具在家配制75度(1度是指100mL的酒液中含有酒精的体积为1mL消毒酒液)。现有一个底面积为100cm2的足够高圆柱形容器,容器中装有10cm高的90度酒液,此时酒液的质量为 g;为了配制75度酒液,小杜将水缓慢加入其中(不考虑混合后体积的变化),则小杜最多可以配制75度酒液 g(已知酒精密度为0.8g/cm3)。
【例7】文文同学对合金制成的机器零件进行探究。她用天平测出一个合金构件的质量为748g,用量杯测出该构件的体积是200cm3,她查阅了该构件说明书,得知该合金构件由铝与钢两种材料合成,钢的体积占比为20%,且铝的密度为2.7×103kg/m3,如果构件的体积等于两种金属体积之和。求:
(1)该合金材料的平均密度是多少kg/m3?
(2)该合金构件中钢的密度是多少kg/m3?
(3)若用该合金材料去替换机器的某一钢制零件,质量比钢制零件减少了832g,求该钢制零件的质量是多少g?
【例8】“玫瑰金”是一种黄金和铜的合金。小庆想买一件如图所示的玫瑰金工艺品送给他的朋友,商店的售货员告诉他们,这件合金工艺品是由金和铜两种金属混合而成的,其含金量为80%(金的质量占金和铜总质量的百分比)。小庆朋友对商店售货员的话表示怀疑,于是便让小庆进行验证。小庆利用所学的物理知识测出了这件工艺品的质量为900g,体积为(为方便计算,假设,)。则下列说法正确的是( )
A.按商店售货员的说法,这件工艺品的体积为
B.根据小庆的实验数据,这件工艺品的密度是
C.按商店售货员的说法,这件工艺品的密度是
D.根据小庆的实验数据,这件工艺品的含金量是70%
【课后巩固】
1.一枚实心纪念币的质量为16g,体积为2cm3,纪念币的密度是 kg/m3,可见,这枚纪念币 (填“是”或“不是”)纯金制。(ρ金=19.3×103kg/m3)
2.小明到市场上购买了2斤蜂蜜,回家用电子秤测质量,果真是2斤。小明想这个蜂蜜肯定没掺水,是纯正的好蜂蜜。你认为小明用测量质量 办法判断蜂蜜是否掺水是 (选填“合理”或“不合理”)的,你的理由是 。
3.利用质量相同的铜和铝,制成体积相等的两个球(ρ铜>ρ铝)。则下列判断正确的是( )
A.铝球一定是空心的
B.铜球一定是空心的
C.铝球一定是实心的
D.若两球都是空心的,则铝球的空心部分体积大
4.a、b是两个由同种材料制成的金属球,它们的质量分别为60g和128g,体积分别为和。在这两个金属球中,如果有一个是实心的,那么( )
A.a是实心球,金属密度是 B.a是实心球,金属密度是
C.b是实心球,金属密度是 D.b是实心球,金属密度是
5.用质量相同的铁、铜、铅制成体积相同的金属球,可能出现的情况是( )(铅、铜、铁密度依次减小)
①如果铜球是实心的,那么铁球一定是空心的
②如果铁球是空心的,那么铜球、铅球一定是空心的
③如果铅球是实心的,则铁球、铜球可能是空心的
④三个球若都是空心的,则空心部分的体积一定是V铅>V铜>V铁
A.①③ B.②④ C.④ D.①④
6.有a、b两个小球分别由、的甲、乙两种材料制成,两小球质量分别为30g和25g,体积之比为,则下列说法正确的是( )
A.若只有一个球是空心,则a球是空心的
B.若只有一个球是空心,则空心球的空心部分与实心部分体积之比为1:4
C.若两球均是空心的,a球的空心部分体积可以比b球的空心部分体积大
D.若只有一个球是空心,将空心球的空心部分装满水后,两球总质量相等
7.下列关于密度说法中正确的是( )
A.水和冰是同种物质,所以它们的密度相同
B.可以利用密度来鉴别物质,因为不同物质的密度一定不同
C.为减轻质量,航空器材常采用强度高、密度大的合金或新型合成材料
D.火灾时,受困人员弯腰撤离,原因是燃烧产生的有害气体温度较高,密度较小
8.用质量均为1kg的水和甲液体(甲液体的密度为0.8×103kg/m3)配制密度为0.9×103kg/m3的乙液体。则最多能配成乙液体 kg。
9.农业上常采用配制适当密度的盐水进行选种。在选稻种时需用密度是1.1×103kg/m3的盐水,现配制了500cm3的盐水,称得它的质量为505g,这样的盐水 (符合/不符合)要求,如不符合要求,应加 (盐/水) g。(ρ食盐=2.2×103kg/m3,不考虑混合后体积的变化)
10.如图甲所示,某“冰块”内有一空心小铁球,冰和铁球的总质量是248g、总体积160cm3,将它们放在盛有水的薄壁圆柱形容器中沉底.当冰全部熔化后,容器里的水面下降了1cm,如图乙所示,已知容器的底面积为10cm2,冰的密度为0.9g/cm3,铁的密度为7.9g/cm3,则“冰块”中冰的质量是 g,小铁球空心部分的体积是 cm3(不计水的蒸发).
11.在复习密度知识应用时,小明认为可以用天平和量筒(如图甲)来鉴别一枚金戒指(约15g左右)是否是纯金制品(ρ金=19.3×103kg/m3)。小华分析后,认为小明的方法无法证明戒指是否是纯金的,小华的理由是 。小明和同学取了一只体积与金戒指大小差不多的金属螺母,利用适量的水、电子天平和细线等器材进行了图中的乙、丙、丁的操作,他们所测的螺母的质量是 g,密度是 kg/m3。
12.小渝妈妈在网上购买了一枚金灿灿的手镯,小渝看到后发出疑问,手镯是黄金的吗?他想到可以通过测量手镯的密度来进行判断。
(1)把天平放在水平台面上,将 移至标尺左端的零刻线处,发现指针指向如图甲所示,他应该向 调节平衡螺母使横梁平衡;
(2)测量手镯质量时,右盘中的砝码和游码的位置如图乙所示,手镯的质量为 g;
(3)手镯太大不能直接用量筒和水测体积,小渝经过思考进行了如下的实验操作:
①将适量水倒入烧杯内,并置于天平上,调节平衡后天平示数为100g;
②用细线系好手镯缓慢浸没到水中保持静止,手镯始终未与烧杯接触,调节平衡后天平示数为109g;
根据测得的数据可以计算出该手镯的密度ρ= kg/m3;若实验中忘了进行第①步测量,取出手镯后才测量烧杯和水的质量,则所计算出的密度比真实值 (选填“偏大”、“偏小”或“不变”);
(4)结合表格二,若该手镯为实心则 (选填“是”或“不是”)纯金的。通过网上查找资料得知,这种金色手镯大多是铜锌合金制成,若妈妈的手镯也是铜锌合金且为实心,则其中含有铜和锌的质量之比为 ;
表二
物质 铝 锌 铁 铜 银 金
密度g/cm3 2.7 7.1 7.9 8.9 10.5 19.3
(5)跟商家投诉后,商家辩称手镯为空心,所以密度才比纯金小,根据你所学到的各学科知识,为进一步验证手镯是否为纯金,请写出你的方法: 。
13.小丽妈妈过年时送给小丽一件纯金挂件“福兔”,小丽想知道这个挂件是实心还是空心,于是她利用天平、量筒进行测量,她的操作如下:
(1)她把天平放在 上,游码拨到零刻度线,发现指针位置如图甲所示,她接下来的第一步操作应该是将平衡螺母向 调(选填“左”或“右”);
(2)她用调好的天平称挂件的质量如图乙,则挂件的质量为 g;
(3)将挂件放入量筒并倒入适量水,如图丙所示。取出挂件,量筒中剩余水的体积为30mL,挂件的体积为 cm3,密度为 g/cm3;
(4)小丽翻书查阅纯金的密度是19.3g/cm3,请你帮助小丽判断一下此挂件是不是实心的,如果是空心的,则空心的体积有多大 。(写出必要的文字说明、表达式及最后结果)
14.小明有一个质量为158g、体积为30cm3的空心铁球。若将该空心铁球压扁,并与一定量的铝混合浇铸形成了一个铁铝合金块,将这个合金块放入一个装满水的容器中,溢出50g水。(已知ρ铁=7.9×103kg/m3,ρ铝=2.7×103kg/m3,ρ冰=0.9×103kg/m3)。求:
(1)铁球空心部分的体积;
(2)将铁球的空心部分充满冰后的总质量;
(3)浇铸的铁铝合金块的平均密度。
15.周末小明去商店购买了一个小铁球,为了判断小铁球是实心还是空心的,小明找来一个质量为100g的空瓶子,装满水后瓶子的总质量为600g。如果把小铁球装进空瓶子中,测得瓶子的总质量为900g,然后在瓶子中装满水,测得瓶子、水和小铁球的总质量为1200g,ρ铁=7.9×103kg/m3,ρ水=1.0×103kg/m3,求:
(1)小铁球的质量;
(2)瓶子的容积;
(3)小铁球的体积;
(4)请你通过计算并判断小球是空心的还是实心的?
16.某种子公司为选种,需要配制密度为的盐水。工作人员先在量筒内放入一定量的纯水,如图甲所示,再加24g盐完全溶解在的量筒内的水中,液面升高后的位置如图乙所示。求:
(1)乙量筒内盐水的质量;
(2)计算说明配制的盐水密度是否符合要求?
(3)若不符合要求需要加水还是加盐,加多少克的水或盐?
1.我国科学家研发的固体浮力材料已成功用于万米深海探测,为深潜器提供浮力,技术水平居于世界前列,固体浮力材料的核心是“微球”(直径很小的空心玻璃球)。若用质量为60g,密度为2.4g/cm3的玻璃制成“微球”后和粘合剂黏合制成一块固体浮力材料,其内部结构的放大示意图如图所示。粘剂的密度为1.2g/cm3,粘合剂体积占固体浮力材料总体积的20%,制成后的固体浮力材料密度为0.48g/cm3。下列说法错误的是( )
A.这块固体浮力材料中所用玻璃的体积是25cm3
B.这块固体浮力材料的总体积是250cm3
C.这块固体浮力材料中粘合剂的质量为60g
D.这块固体浮力材料中空心部分的体积为200cm3
2.西贝同学测量密度时,先用天平测得装满水的溢水杯质量为500g,将一空心金属块缓慢浸没在溢水杯中,稳定后,用天平测得溢水杯的总质量为750g,然后将金属块从溢水杯中取出(假设取出时不带水),再次测得溢水杯的总质量为440g,若将空心部分填满酒精,则金属球的质量变为326g,则空心部分的体积为 cm3,该金属材料的密度为 kg/m3。(已知ρ酒精=0.8g/cm3)
3.白酒的主要成分是水和酒精。目前中国使用白酒的度数表示法称为标准酒度,是指在温度为20℃的条件下,每100mL白酒中所含酒精的毫升数,酒厂为得到相应的酒度,需将高度白酒与低度白酒进行勾兑(混合)。现有60度高度白酒和20度低度白酒若干(已知ρ酒精=0.8×103kg/m3,ρ水=1.0×103kg/m3,不考虑白酒混合前后体积变化),则100mL的60度白酒中所含酒精体积是 mL,60度白酒的平均密度是 g/cm3;20度白酒密度 (大于/等于/小于)60度白酒密度;如果用60度和20度这两种白酒进行勾兑,获得1000mL 52度的白酒,那么所用60度白酒的质量是 kg。
4.如图所示,两个完全相同的圆柱形容器A与B,它们的底面积为,高8cm,放在水平桌面上。已知A容器装有5.2cm深的水,B容器装有2.8cm深的盐水,盐水质量为340g。现将一块体积为的铁块浸没在B容器的盐水中,B容器中有盐水溢出,将溢出的盐水完全收集后倒入A容器,再将一块总质量为240g的夹杂有小石块的不规则冰块完全浸没于A中,此时冰未熔化,A容器液面恰好与杯口相平。经过很长一段时间,冰块熔化,石块沉底,相比于冰熔化前水面下降0.1cm。(不考虑盐水与水混合后体积的变化,,ρ冰=0.9g/cm3)求:
(1)A容器中水的质量为多少g?
(2)该“冰包石”的平均密度为多少?
(3)现将B中剩余盐水倒入A中,整个过程中液体不能溢出,则A中新溶液密度最大为多少?
5.如图所示,桌面上有一质量100g、高8cm、底面积的薄壁柱形容器,容器内装有5cm深的某混合液体200g。将一个金属实心圆柱体慢慢放入容器与底部接触,溢出部分液体,且圆柱体有一半露出液面。此时容器、容器内液体、圆柱体的总质量为1570g,慢慢取出圆柱体后,容器与容器内液体总质量为220g,忽略取出圆柱体时带出的液体。
(1)求混合液体的密度;
(2)求金属块的密度;
(3)若原容器中的混合液体是由水与密度为的液体X配制而来,且水的体积分数(水的体积占混合液总体积的百分比)需控制在40%至60%的范围内,求液体X的密度的取值范围(已知水的密度为),不考虑分子间隙等次要因素,最终结果保留一位小数)。
6.如图所示,底面积为3×10-2m2、高为0.12m的薄壁柱形容器甲和边长为0.1m的实心均匀正方体乙放在水平地面上,甲容器内盛有0.1m深的水。ρ乙=6.75×103kg/m3,ρ水=1.0×103kg/m3。
(1)求甲容器内水的质量;
(2)将实心均匀正方体乙浸没在甲容器的水中(乙不吸水),求溢出水的体积;
(3)若沿正方体乙的上表面向内部挖去一底面积为0.006m2、高为h的长方体丙,并在乙中加满水,是否有可能使加满水后乙的质量与长方体丙的质量相等?若有可能,算出h的值,若不可能,请通过计算说明原因。
7.阅读短文,回答问题
盖 吕萨克酒度
目前国际上白酒的度数表示法有三种,其中一种称为标准酒度,是指在通常条件下,每100毫升白酒中所含酒精量的毫升数,即白酒中酒精和白酒的体积百分比。中国也使用这种表示法,它是法国著名化学家盖 吕萨克制定的,又称盖 吕萨克酒度。
通常白酒的制作流程是将发酵出的低度数的酒液利用如图甲所示的装置蒸馏成高度数的酒液,再根据需要与水或低度酒进行勾兑。勾兑一方面为了保障酒的品质,另一方面可以调整酒的度数。勾兑好的就要密封保存,一旦打开酒瓶瓶盖,会闻到酒精的气味,瓶盖开启时间越长,就越会影响酒的酒度和密度。
说明:已知ρ酒精=0.8×103kg/m3,以下解题过程中,酒液中的微量元素和酒液混合后总体积的微小变化等因素均忽略不计。
(1)如图乙所示,是物质三种状态下的物理模型,与蒸馏过程中酒分子实际变化情况相对应的顺序是 ;
A.ab B.bca C.bab D.cb
(2)将一烧杯白酒放置一段时间,考虑到酒中水和酒精都会挥发,且酒精挥发更快,则可推断杯中剩余酒的标准酒度会 ,密度会 ,(均选填“变大”、“不变”或“变小”);
(3)测得某次蒸馏后接受罐中酒液的密度为0.88×103kg/m3,则该次酒液的标准酒度为 %。如果要将该酒液的度数勾兑成50%,则应往该酒液中加 (选填“水”或“酒精”);
(4)若现用30%和60%的酒液进行勾兑,要获得42%的白酒1000mL。则需要30%的酒液 mL,
,需要60%的酒液 g。
【课后评价】
这节课我给自己☆☆☆☆☆颗星。
【参考答案】
自主学习
一、利用密度求出质量:质量
二、利用密度求出体积:体积
三、利用密度鉴别物质:可能、气味
【例1】A 【例2】C 【例3】D 【例4】(1)50cm3;(2)2g/cm3;(3)0.5cm
【例5】C 【例6】800、1020 【例7】(1)3.74g/cm3;(2)7.9×103kg/m3;(3)1580g
【例8】A
课后巩固
基础练习
1. 8×103、不是 2. 不合理、应该测量密度判断蜂蜜是否掺水 3. B 4. C 5. B 6. D 7. D
8. 1.8 9. 不符合、 盐、90 10. 90、 40
11. 金戒指的体积小于量筒的分度值、7.2、8×103
12. (1)游码、左;(2)72;(3)、偏小;(4)不是 、89︰71;(5)金手镯也可以通过测硬度来鉴别,金手镯的成色越高,质地会越柔软,硬度会越小,很容易被折弯。而成色差的金手镯硬度会比较大,不容易被折弯。(熔化它也行)
13. (1)水平台、左;(2)77.2 ;(3)6、12.9 ;(4)空心,空心的体积为2cm3
14. (1);(2);(3)
15. (1)800g ;(2);(3)200cm3;(4)空心
16. (1)84g;(2)不符合要求;(3)加水,加水70g
能力提升
1. D
2. 20 、
3. 60、0.88、大于、0.704
4. (1)520g;(2);(3)
5. (1)0.8g/cm3;(2)1.6875 g/cm3;(3)0. 5~0.7g/cm3
6. (1)3kg;(2)4×10-4m3;(3)0.09m
7. (1)C; (2)变小、变大;(3)60、水;(4)600、352
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
