第三单元《角的度量》(解题篇五大题型)单元复习讲义(知识梳理+典例精讲+专项精练)-2024-2025学年四年级数学上册(人教版)(学生版+解析)
文档属性
| 名称 | 第三单元《角的度量》(解题篇五大题型)单元复习讲义(知识梳理+典例精讲+专项精练)-2024-2025学年四年级数学上册(人教版)(学生版+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-18 08:26:02 | ||
图片预览



文档简介
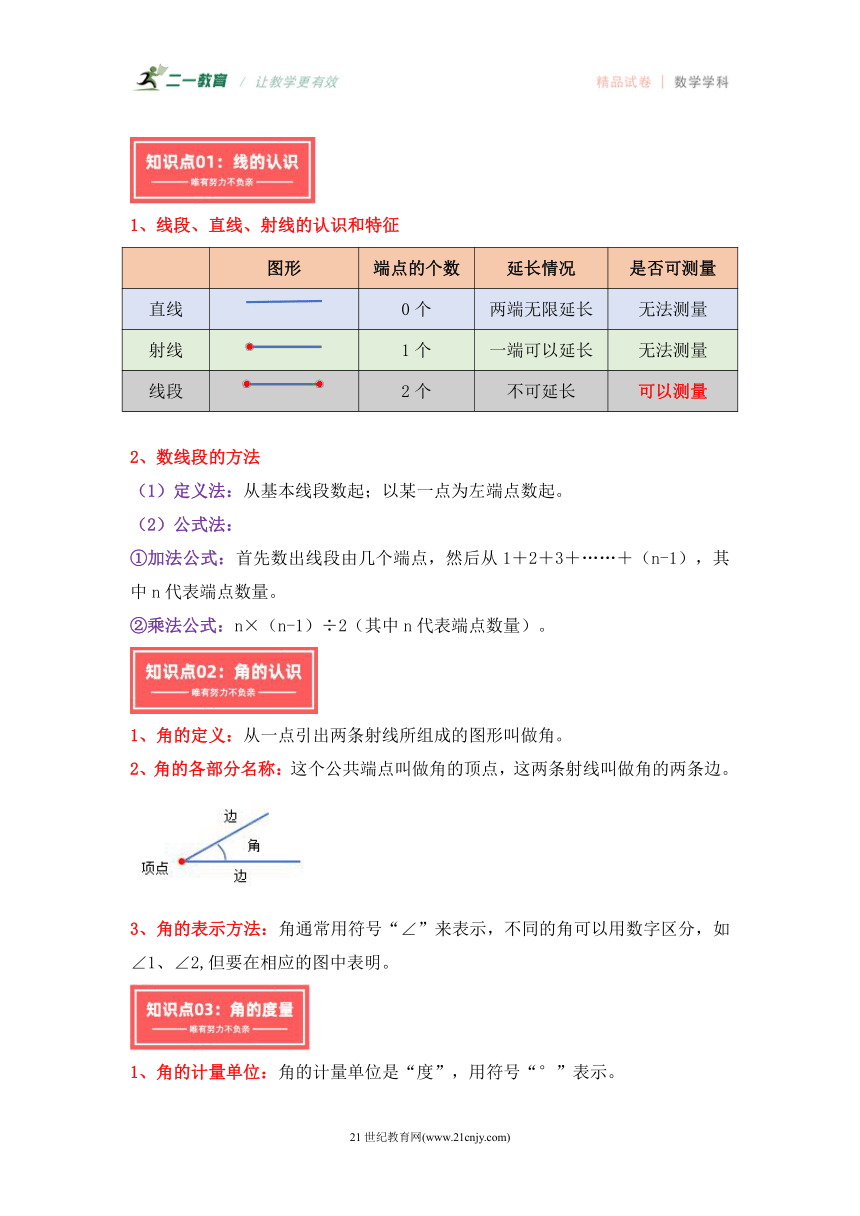
第三单元 《角的度量》 单元复习讲义(讲义)
四年级数学上册专项精练(知识梳理+典例精讲+专项精练)
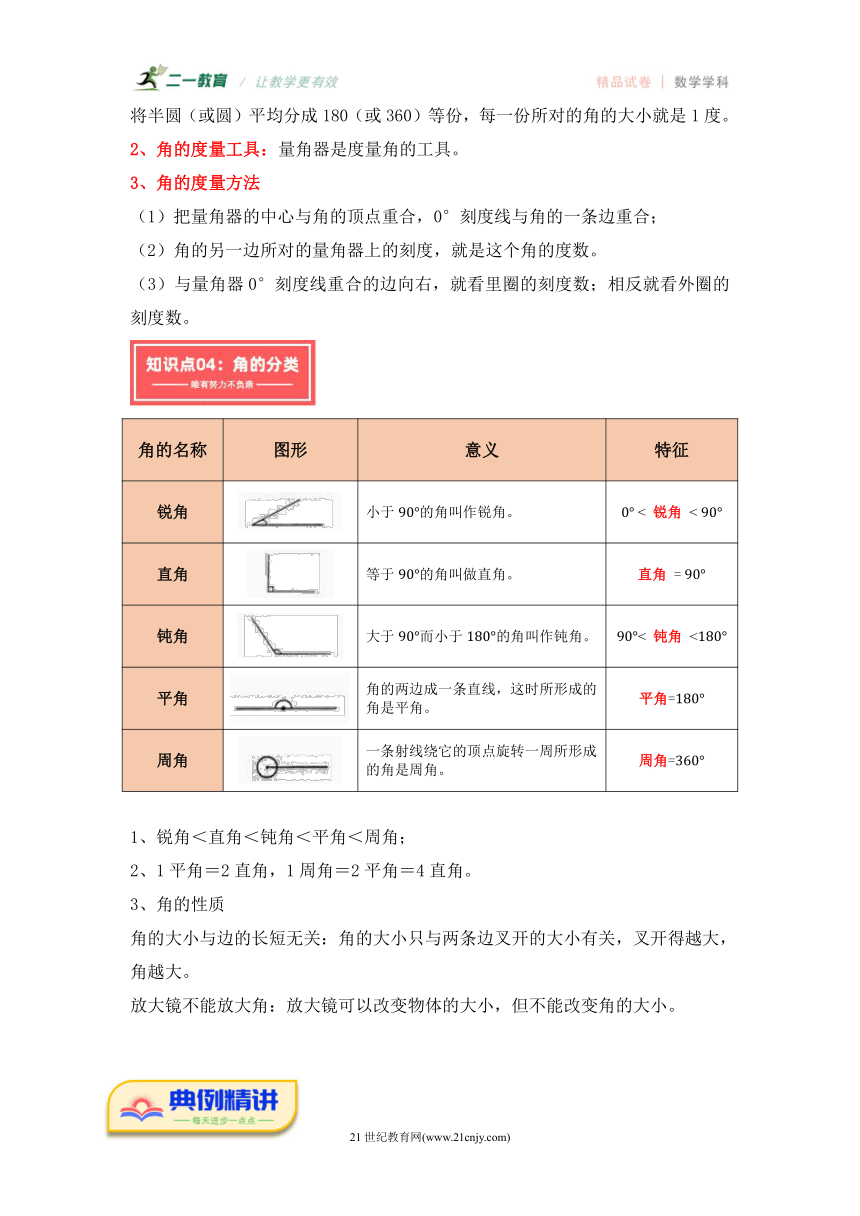
线段、直线、射线的认识和特征
图形 端点的个数 延长情况 是否可测量
直线 0个 两端无限延长 无法测量
射线 1个 一端可以延长 无法测量
线段 2个 不可延长 可以测量
2、数线段的方法
(1)定义法:从基本线段数起;以某一点为左端点数起。
(2)公式法:
①加法公式:首先数出线段由几个端点,然后从1+2+3+……+(n-1),其中n代表端点数量。
②乘法公式:n×(n-1)÷2(其中n代表端点数量)。
1、角的定义:从一点引出两条射线所组成的图形叫做角。
2、角的各部分名称:这个公共端点叫做角的顶点,这两条射线叫做角的两条边。
3、角的表示方法:角通常用符号“∠”来表示,不同的角可以用数字区分,如∠1、∠2,但要在相应的图中表明。
1、角的计量单位:角的计量单位是“度”,用符号“°”表示。
将半圆(或圆)平均分成180(或360)等份,每一份所对的角的大小就是1度。
2、角的度量工具:量角器是度量角的工具。
3、角的度量方法
(1)把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合;
(2)角的另一边所对的量角器上的刻度,就是这个角的度数。
(3)与量角器0°刻度线重合的边向右,就看里圈的刻度数;相反就看外圈的刻度数。
角的名称 图形 意义 特征
锐角 小于的角叫作锐角。 < 锐角 <
直角 等于的角叫做直角。 直角 =
钝角 大于而小于的角叫作钝角。 < 钝角 <
平角 角的两边成一条直线,这时所形成的角是平角。 平角=
周角 一条射线绕它的顶点旋转一周所形成的角是周角。 周角=
1、锐角<直角<钝角<平角<周角;
2、1平角=2直角,1周角=2平角=4直角。
3、角的性质
角的大小与边的长短无关:角的大小只与两条边叉开的大小有关,叉开得越大,角越大。
放大镜不能放大角:放大镜可以改变物体的大小,但不能改变角的大小。
【典例精讲1】(23-24四年级上·四川乐山·期中)先画第一条长为2厘米的线段,再画第二条线段的长度是第一条线段的5倍。第二条线段长是多少分米?
【答案】画图见详解;1分米
【分析】根据线段的含义,线段有2个端点,有限长,画出一条2厘米的线段,再画第二条线段的长度是第一条线段5倍的线段,即2×5=10厘米的线段,然后根据1分米=10厘米,将厘米换算分米,即可求出第二条线段长是多少分米。
【详解】(1)
(2)2×5=10(厘米)
10厘米=1分米
答:第二条线段长是1分米。
【典例精讲2】(19-20四年级上·湖北十堰·期末)由一点引出的3条射线,可以组成多少个角?由一点引出10条射线,可以组成多少个角?
【答案】3个;45个
【分析】从一点出发引出3条射线,每一条射线都分别与其它的射线组成一个角,所以3条射线就可以组成2+1=3个角;
从一点出发引出10条射线,每一条射线都分别与其它的射线组成一个角,依此可得组成角的个数是9+8+7+6+5+4+3+2+1=45个角。
【详解】2+1=3(个)
9+8+7+6+5+4+3+2+1
=(9+1)×9÷2
=10×9÷2
=90÷2
=45(个)
答:由一点引出的3条射线,可以组成3个角;由一点引出10条射线,可以组成45个角。
【点睛】本题考查了数角的概念,要有总结规律的能力或公式应用的能力。
【典例精讲3】(23-24四年级上·山西晋中·期中)小华在使用量角器测量∠1时,用量角器的0刻度线与∠1的一条边重合,然后顺着0刻度线向上看,∠1的另一边对着125°这条刻度线。小红在测量∠2时,用量角器10°刻度线与∠2的一条边重合,然后顺着10°刻度线向上看,∠2的另一条边对准130°这条刻度线,两人读数都正确,你能判断∠1和∠2两个角哪个角大,哪个角小吗?
【答案】∠1大;∠2小
【分析】量角的步骤是:先把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合,角的另一边所对的量角器上的刻度,就是这个角的度数,依此计算出∠1的度数;然后用130°减10°,从而计算出∠2的度数,最后再比较即可。
【详解】根据题意可知,∠1=125°。
∠2=130°-10°=120°
125°>120°
答:∠1大,∠2小。
【典例精讲4】(22-23四年级上·江西吉安·期末)下面是一张长方形纸折起来以后形成的图形,已知:∠1和一个145°的角正好可拼成一个平角,求∠1和∠2的度数。
【答案】∠1=35°;∠2=20°
【分析】1直角=90°,1平角=180°,根据题意可知:∠1+145°=180°,因此∠1=180°-145°;∠1+∠1+∠2=90°,因此用90°减去2个∠1即可得到∠2的度数,依此计算。
【详解】∠1=180°-145°=35°;
35°+35°=70°
90°-70°=20°
答:∠1=35°,∠2=20°。
【点睛】此题考查的是角的分类与换算,熟练掌握平角、直角的特点是解答此题的关键。
【典例精讲5】(23-24四年级上·河南新乡·期中)一个平角由两个角拼成,其中一个角是45度,另一个角是多少度?
【答案】135度
【分析】平角等于180度,因此用180度减去其中一个角的度数,即可计算出另一个角的度数;据此解答。
【详解】180-45=135(度)
答:另一个角是135度。
学校:___________ 姓名:___________ 班级:___________
解答题
1.(23-24四年级上·广东佛山·期末)张叔叔是个台球迷,他发现当台球撞击桌边时就会向另一个方向弹走,如图所示:
(1)已知∠1=45°,∠3=50°,请你量一量,∠2=( ),∠4=( )。
(2)如上图,台球撞向桌边的路线与桌边形成了一个角,它弹走的路线与桌边也形成了一个角,你发现( )。
(3)请运用你发现的规律在上面图3中画出台球向另一个方向弹走的角度和路线。
2.(23-24四年级上·四川·期中)两个正方形相交如下图,∠2大小未知,∠1与∠3相等吗?
3.(23-24四年级上·全国·单元测试)下图是一张长方形纸折起来后的图形,已知∠1=50°,求∠2的度数。
4.(22-23四年级上·广东揭阳·期中)已知∠1=32°,∠2=38°,求∠3的度数。
5.(23-24四年级上·陕西咸阳·期中)如图,欢欢要从家出发去奇奇家玩。最短的路线是几号?为什么?
6.(23-24四年级上·云南昆明·期中)已知∠3=60°,∠5=30°。求∠1、∠2、∠4的度数。
7.(23-24四年级上·湖南怀化·期末)如图:已知∠1=50°,求∠2的度数。
8.(23-24四年级上·河南信阳·期末)将一副三角板中的两块直角三角尺按下图两种方式摆放。
(1)求图1中∠1和∠2的度数。
(图1)
(2)猜想图2中∠1和∠2的数量关系,通过计算说明理由。
(图2)
9.(22-23四年级上·河南驻马店·期末)两只蚂蚁夺旗,它们的位置如图所示。
10.(23-24四年级上·河北邯郸·期末)红星小学位于劳动路与南山大道的交叉口,下图是红星小学的位置示意图。
(1)用量角器量出∠1=( )°。
(2)张师傅要给红星小学送纯净水,请你为张师傅设计一条最近的路。
11.(23-24四年级上·全国·单元测试)如下图,∠2是∠1的2倍,∠3是∠1的6倍,求∠1、∠2和∠3的度数。
12.(23-24四年级上·安徽黄山·期末)在下图中按要求画图,并解决问题。
(1)画出直线AB。
(2)画出射线BC。
(3)画好的图形中有( )种角。在图中指出并写出角的名称。
13.(22-23四年级上·全国·课后作业)小乐用一副三角尺在一块长方形纸板上拼出了下面的图形(图中的阴影部分),爸爸说∠1=30°,请求出∠2的度数。
14.(22-23四年级上·河南洛阳·期末)用量角器量一量下面的角,再比一比,说说自己的发现。
我发现:( )。
15.(22-23四年级上·北京·单元测试)如果两条平行线被一条直线所截(如图),会产生很多个有联系的角。
(1)请用量角器测量∠1、∠2,你发现了什么?
(2)根据上面得到的结论,观察∠3、∠5,通过推理说明∠3和∠5的关系。
16.(22-23四年级上·广东广州·期末)如图,在长方形ABCD中已知∠1=80°,∠5=40°。分别求出∠2、∠3和∠6的度数。
17.(22-23四年级上·辽宁抚顺·期末)按要求完成下列内容。
(1)量出∠1=( )°。
(2)求出∠2、∠3、∠4的度数。
(3)你发现了什么?
18.(22-23四年级上·浙江杭州·期中)下面图中的∠1与∠2是不是相等?说明理由。
19.(22-23四年级上·湖北省直辖县级单位·期中)如图所示,已知∠1=35°,求∠2、∠3、∠4的度数。
20.(22-23四年级上·山东菏泽·期中)如图,已知,求、、的度数。
21.(23-24四年级上·河南新乡·期中)∠1和∠2组成一个平角,∠2的度数是∠1的4倍,∠1和∠2各是多少度?
22.(23-24四年级上·河南南阳·期中)乐乐把两张硬纸条订在一起,组成了一个37°的角,同桌欢欢在乐乐摆的基础上旋转其中一条边,所形成的角的度数比乐乐的4倍还大12°,这个角是多少度?是什么角?
23.(23-24四年级上·山东菏泽·期中)测量下面各角的度数,你发现了什么?
∠1=( ),∠2=( ),∠3=( )。
发现:
24.(23-24四年级上·云南玉溪·期中)已知∠1=25°,求∠2、∠3、∠5各等于多少度。
25.(23-24四年级上·江苏宿迁·期末)把一张长方形纸的一个角折起来(如图),已知∠2=130°,则∠1是多少度?
26.(24-25四年级上·全国·单元测试)有∠1、∠2、∠3三个角,其中∠1的度数最大,∠2比直角小,∠3既不是锐角也不是钝角。这三个角分别可能是什么样的角?
21世纪教育网(www.21cnjy.com)
第三单元 《角的度量》 单元复习讲义(讲义)
四年级数学上册专项精练(知识梳理+典例精讲+专项精练)
线段、直线、射线的认识和特征
图形 端点的个数 延长情况 是否可测量
直线 0个 两端无限延长 无法测量
射线 1个 一端可以延长 无法测量
线段 2个 不可延长 可以测量
2、数线段的方法
(1)定义法:从基本线段数起;以某一点为左端点数起。
(2)公式法:
①加法公式:首先数出线段由几个端点,然后从1+2+3+……+(n-1),其中n代表端点数量。
②乘法公式:n×(n-1)÷2(其中n代表端点数量)。
1、角的定义:从一点引出两条射线所组成的图形叫做角。
2、角的各部分名称:这个公共端点叫做角的顶点,这两条射线叫做角的两条边。
3、角的表示方法:角通常用符号“∠”来表示,不同的角可以用数字区分,如∠1、∠2,但要在相应的图中表明。
1、角的计量单位:角的计量单位是“度”,用符号“°”表示。
将半圆(或圆)平均分成180(或360)等份,每一份所对的角的大小就是1度。
2、角的度量工具:量角器是度量角的工具。
3、角的度量方法
(1)把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合;
(2)角的另一边所对的量角器上的刻度,就是这个角的度数。
(3)与量角器0°刻度线重合的边向右,就看里圈的刻度数;相反就看外圈的刻度数。
角的名称 图形 意义 特征
锐角 小于的角叫作锐角。 < 锐角 <
直角 等于的角叫做直角。 直角 =
钝角 大于而小于的角叫作钝角。 < 钝角 <
平角 角的两边成一条直线,这时所形成的角是平角。 平角=
周角 一条射线绕它的顶点旋转一周所形成的角是周角。 周角=
1、锐角<直角<钝角<平角<周角;
2、1平角=2直角,1周角=2平角=4直角。
3、角的性质
角的大小与边的长短无关:角的大小只与两条边叉开的大小有关,叉开得越大,角越大。
放大镜不能放大角:放大镜可以改变物体的大小,但不能改变角的大小。
【典例精讲1】(23-24四年级上·四川乐山·期中)先画第一条长为2厘米的线段,再画第二条线段的长度是第一条线段的5倍。第二条线段长是多少分米?
【答案】画图见详解;1分米
【分析】根据线段的含义,线段有2个端点,有限长,画出一条2厘米的线段,再画第二条线段的长度是第一条线段5倍的线段,即2×5=10厘米的线段,然后根据1分米=10厘米,将厘米换算分米,即可求出第二条线段长是多少分米。
【详解】(1)
(2)2×5=10(厘米)
10厘米=1分米
答:第二条线段长是1分米。
【典例精讲2】(19-20四年级上·湖北十堰·期末)由一点引出的3条射线,可以组成多少个角?由一点引出10条射线,可以组成多少个角?
【答案】3个;45个
【分析】从一点出发引出3条射线,每一条射线都分别与其它的射线组成一个角,所以3条射线就可以组成2+1=3个角;
从一点出发引出10条射线,每一条射线都分别与其它的射线组成一个角,依此可得组成角的个数是9+8+7+6+5+4+3+2+1=45个角。
【详解】2+1=3(个)
9+8+7+6+5+4+3+2+1
=(9+1)×9÷2
=10×9÷2
=90÷2
=45(个)
答:由一点引出的3条射线,可以组成3个角;由一点引出10条射线,可以组成45个角。
【点睛】本题考查了数角的概念,要有总结规律的能力或公式应用的能力。
【典例精讲3】(23-24四年级上·山西晋中·期中)小华在使用量角器测量∠1时,用量角器的0刻度线与∠1的一条边重合,然后顺着0刻度线向上看,∠1的另一边对着125°这条刻度线。小红在测量∠2时,用量角器10°刻度线与∠2的一条边重合,然后顺着10°刻度线向上看,∠2的另一条边对准130°这条刻度线,两人读数都正确,你能判断∠1和∠2两个角哪个角大,哪个角小吗?
【答案】∠1大;∠2小
【分析】量角的步骤是:先把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合,角的另一边所对的量角器上的刻度,就是这个角的度数,依此计算出∠1的度数;然后用130°减10°,从而计算出∠2的度数,最后再比较即可。
【详解】根据题意可知,∠1=125°。
∠2=130°-10°=120°
125°>120°
答:∠1大,∠2小。
【典例精讲4】(22-23四年级上·江西吉安·期末)下面是一张长方形纸折起来以后形成的图形,已知:∠1和一个145°的角正好可拼成一个平角,求∠1和∠2的度数。
【答案】∠1=35°;∠2=20°
【分析】1直角=90°,1平角=180°,根据题意可知:∠1+145°=180°,因此∠1=180°-145°;∠1+∠1+∠2=90°,因此用90°减去2个∠1即可得到∠2的度数,依此计算。
【详解】∠1=180°-145°=35°;
35°+35°=70°
90°-70°=20°
答:∠1=35°,∠2=20°。
【点睛】此题考查的是角的分类与换算,熟练掌握平角、直角的特点是解答此题的关键。
【典例精讲5】(23-24四年级上·河南新乡·期中)一个平角由两个角拼成,其中一个角是45度,另一个角是多少度?
【答案】135度
【分析】平角等于180度,因此用180度减去其中一个角的度数,即可计算出另一个角的度数;据此解答。
【详解】180-45=135(度)
答:另一个角是135度。
学校:___________ 姓名:___________ 班级:___________
解答题
1.(23-24四年级上·广东佛山·期末)张叔叔是个台球迷,他发现当台球撞击桌边时就会向另一个方向弹走,如图所示:
(1)已知∠1=45°,∠3=50°,请你量一量,∠2=( ),∠4=( )。
(2)如上图,台球撞向桌边的路线与桌边形成了一个角,它弹走的路线与桌边也形成了一个角,你发现( )。
(3)请运用你发现的规律在上面图3中画出台球向另一个方向弹走的角度和路线。
【答案】(1)45°;50°
(2)这两个角相等
(3)见详解
【分析】(1)量角器可以分别量出∠2、∠4的度数(把量角器的中心与角的顶点重合,刻度线与边的一边重合,角的另一边所经过的量角器上所显示的刻度就是被量角的度数)。
(2)根据量出的各角度数,台球撞向桌边的路线与桌边形成了一个角,它弹走的路线也与桌边形成了一个角,两个角度数相同,据此解答。
(3)根据以上发现,即可完成如图的台球运动线路图。
【详解】(1)已知∠1=45°,∠3=50°,经测量∠2=45°,∠4=50°。
台球撞向桌边的路线与桌边形成了一个角,它弹走的路线与桌边也形成了一个角,发现这两个角相等。
(3)如图:
2.(23-24四年级上·四川·期中)两个正方形相交如下图,∠2大小未知,∠1与∠3相等吗?
【答案】∠1与∠3相等
【分析】观察图形可得∠1+∠2=90°,∠3+∠2=90°,分别表示出∠1和∠3的大小,比较即可得出答案。
【详解】观察图形可得∠1+∠2=90°,∠3+∠2=90°,
所以∠1=90°-∠2,∠3=90°-∠2,
即∠1=∠3,
答:∠1与∠3相等
【点睛】本题的关键是熟练掌握角度的计算。
3.(23-24四年级上·全国·单元测试)下图是一张长方形纸折起来后的图形,已知∠1=50°,求∠2的度数。
【答案】65°
【分析】由对折的性质可知,∠2挡住的角就等于∠2,因为三个角的度数和是平角,平角=180°,∠1=50°,所以180°-50°=130°,∠2=130°÷2=65°。
【详解】(180°-50°)÷2
=130°÷2
=65°
答:∠2的度数是65°。
4.(22-23四年级上·广东揭阳·期中)已知∠1=32°,∠2=38°,求∠3的度数。
【答案】110°
【分析】根据题图可知,∠1、∠2和∠3组成一个平角,则∠3=180°-∠2-∠1。
【详解】∠3=180°-∠2-∠1=180°-38°-32°=110°
答:∠3的度数是110°。
【点睛】解决此类问题时,要善于利用图中隐藏的特殊角(直角、平角、周角),以及它与各角之间的关系,利用已知角,求出未知角。
5.(23-24四年级上·陕西咸阳·期中)如图,欢欢要从家出发去奇奇家玩。最短的路线是几号?为什么?
【答案】③;两点之间的所有连线中,线段最短。
【分析】根据线段的定义及特征可知,两点之间的所有连线中,线段最短,据此解答即可。
【详解】欢欢要从家出发去奇奇家玩的五条路中,只有③是线段,而两点之间,线段最短。即可得出答案。
6.(23-24四年级上·云南昆明·期中)已知∠3=60°,∠5=30°。求∠1、∠2、∠4的度数。
【答案】60°;120°;90°
【分析】用平角的度数减去∠3和∠5的度数,即可求出∠4的度数,再用平角的度数减去∠3的度数,即可求出∠2的度数,用平角的度数减去∠2的度数,即可求出∠1的度数,代入数据计算。
【详解】∠2=180°-60°=120°
∠1=180°-120°=60°
∠4=180°-60°-30°=90°
答:∠1的度数是60°,∠2的度数是120°,∠4的度数是90°。
7.(23-24四年级上·湖南怀化·期末)如图:已知∠1=50°,求∠2的度数。
【答案】80°
【分析】将长方形纸折起一部分,则折起后的∠1与折起前的角的度数是相同的,都是50°,又这三个角组成了一个平角,据此即可求出∠2的度数。
【详解】结合分析可知,由于∠2与另外两个角组成了一个平角,平角的度数是180°,故∠2=180°-50°-50°=80°。
8.(23-24四年级上·河南信阳·期末)将一副三角板中的两块直角三角尺按下图两种方式摆放。
(1)求图1中∠1和∠2的度数。
(图1)
(2)猜想图2中∠1和∠2的数量关系,通过计算说明理由。
(图2)
【答案】(1)∠1=120°;∠2=135°
(2)∠1=∠2。
在含有45°三角尺中,∠1+∠3=90°,在含有30°的三角尺中,∠2+∠3=90°;
所以∠1+∠3=∠2+∠3=90°,则∠1=∠2。
【分析】(1)根据图中哪两个角组成平角,利用平角减去已知角来依次计算出所要求的角的度数。平角是等于180°的角,已知三角尺中的60°角和∠1形成平角,用平角减去60°,即可求出∠1的度数,三角板中的45°角和∠2形成平角,用平角减去45°,即可求出∠2的度数。
(2)两个三角板都有一个直角,∠1+∠3=90°,∠2+∠3=90°,∠3重合,∠1=∠2。
【详解】(1)∠1=180°-60°=120°,∠2=180°-45°=135°
(2)∠1=∠2。
在含有45°三角尺中,∠1+∠3=90°,在含有30°的三角尺中,∠2+∠3=90°
所以∠1+∠3=∠2+∠3=90°,则∠1=∠2。
9.(22-23四年级上·河南驻马店·期末)两只蚂蚁夺旗,它们的位置如图所示。
【答案】不公平,因为乙蚂蚁与旗的距离短一些。
【分析】甲、乙两只蚂蚁夺旗,要想游戏规则公平,甲、乙蚂蚁与旗的距离必须相等,由图可知距离长短,据此解答。
【详解】答:由图可以看出,不公平,因为乙蚂蚁与旗的距离短一些。
10.(23-24四年级上·河北邯郸·期末)红星小学位于劳动路与南山大道的交叉口,下图是红星小学的位置示意图。
(1)用量角器量出∠1=( )°。
(2)张师傅要给红星小学送纯净水,请你为张师傅设计一条最近的路。
【答案】(1)130
(2)见详解
【分析】(1)量角器的中心与角的顶点重合,0刻度线与角的一边重合,角的另一边所对的量角器上的刻度,就是这个角的度数;用量角器量出∠1的度数即可解答。
(2)两点之间线段最短,沿纯净水站到红星小学的线段走最近,据此画出即可解答。
【详解】(1)经测量,∠1=130°。
(2)
11.(23-24四年级上·全国·单元测试)如下图,∠2是∠1的2倍,∠3是∠1的6倍,求∠1、∠2和∠3的度数。
【答案】∠1=20°;∠2=40°;∠3=120°
【分析】根据题意,∠2和∠3都以∠1为标准量,所以把∠1的度数看作1份,则∠2就是2份,∠3就是6份;一共就是(1+2+6)份;从图中可以看出,三个角组成了平角,总度数为180°,所以用总度数180°除以总份数,得到其中一份的度数,即∠1的度数,再用∠1的度数分别乘2和6,即得到∠2和∠3的度数。据此解答。
【详解】180°÷(1+2+6)
=180°÷(3+6)
=180°÷9
=20°
20°×2=40°
20°×6=120°
所以,∠1=20°;∠2=40°;∠3=120°。
12.(23-24四年级上·安徽黄山·期末)在下图中按要求画图,并解决问题。
(1)画出直线AB。
(2)画出射线BC。
(3)画好的图形中有( )种角。在图中指出并写出角的名称。
【答案】(1)见详解
(2)见详解
(3)3;见详解
【分析】(1)过点A、点B画一条直的线即可;
(2)以点B为端点,过点C画一条直的线即可;
(3)两条边在一条直线上的角是平角,小于90°的角是锐角,大于90°小于180°的角是钝角;根据(1)和(2)画出的图可以看出,以A点为顶点的角是平角,∠CBA为锐角,与∠CBA有公共边BC,且与∠CBA组成平角的角是钝角,所以图形中有3种角,据此即可解答。
【详解】(1)(2)见下图:
(3)画好的图形中有3种角。图见(1)(2)。
13.(22-23四年级上·全国·课后作业)小乐用一副三角尺在一块长方形纸板上拼出了下面的图形(图中的阴影部分),爸爸说∠1=30°,请求出∠2的度数。
【答案】45°
【分析】根据题图可知,∠1、∠2和三角尺中60°、45°的角组成一个平角,则∠2=180°-∠1-60°-45°。
【详解】∠2=180°-∠1-60°-45°=180°-30°-60°-45°=45°
【点睛】解决此类问题时,要善于利用图中隐藏的特殊角(直角、平角、周角)、三角尺中各个角,以及它与各角之间的关系,利用已知角,求出未知角。
14.(22-23四年级上·河南洛阳·期末)用量角器量一量下面的角,再比一比,说说自己的发现。
我发现:( )。
【答案】40°;40°;40°
角的大小与边的长短无关,只与两边张开的程度有关。
【分析】量角的步骤:先把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合。再看角的另一边所对的量角器上的刻度,就是这个角的度数。据此量出三个角的度数,再进行解答。
【详解】这三个角的度数分别是40°、40°、40°,度数相等,但是角的两条边的长度不相等,说明角的大小与边的长短无关,只与两边张开的程度有关。
【点睛】本题考查用量角器测量角的度数的方法以及角的认识,角两边张开程度不变,边的长度改变,角的大小不变。
15.(22-23四年级上·北京·单元测试)如果两条平行线被一条直线所截(如图),会产生很多个有联系的角。
(1)请用量角器测量∠1、∠2,你发现了什么?
(2)根据上面得到的结论,观察∠3、∠5,通过推理说明∠3和∠5的关系。
【答案】(1)∠1=∠2
(2)∠3=∠5
【分析】(1)分别量出∠1、∠2的度数,再比较大小即可;
(2)平角=180°,∠1加∠3为平角,∠2加∠5为平角,根据平角的定义,再判断∠3、∠5的大小关系即可;据此解答。
【详解】(1)∠1=150°,∠2=150°
所以∠1=∠2。
答:我发现了∠1=∠2。
(2)因为∠1+∠3=180°,∠2+∠5=180°
又因为∠1=∠2,所以∠3=∠5。
答:∠3=∠5。
【点睛】能熟练用量角器量角的度数,是解答此题的关键。
16.(22-23四年级上·广东广州·期末)如图,在长方形ABCD中已知∠1=80°,∠5=40°。分别求出∠2、∠3和∠6的度数。
【答案】100°;80°;50°
【分析】∠1和∠2组成平角,平角是180°,∠2=180°-∠1;
∠2和∠3组成平角,平角是180°,∠3=180°-∠2;
长方形的四个角是直角为90°,∠6=90°-∠5,依此解答即可。
【详解】因为∠1=80°,所以,∠2=180°-80°=100°;
∠3=180°-∠2=180°-100°=80°;
因为∠5=40°,所以,∠6=90°-40°=50°;
答:∠2=100°;∠3=80°;∠6=50°。
【点睛】明白平角和直角的度数,找到对应组成的角是解题关键。
17.(22-23四年级上·辽宁抚顺·期末)按要求完成下列内容。
(1)量出∠1=( )°。
(2)求出∠2、∠3、∠4的度数。
(3)你发现了什么?
【答案】(1)30
(2)∠2=150°;∠3=30°;∠4=150°
(3)∠1=∠3,∠2=∠4
【分析】(1)量角的步骤:先把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合。再看角的另一边所对的量角器上的刻度,就是这个角的度数。
(2)∠1和∠2组成一个平角,则∠2=180°-∠1。∠3和∠2组成一个平角,则∠3=180°-∠2。∠1和∠4组成一个平角,则∠4=180°-∠1。
(3)这四个角中,∠1=∠3,∠2=∠4。
【详解】(1)量出∠1=30°。
(2)∠2=180°-∠1=180°-30°=150°
∠3=180°-∠2=180°-150°=30°
∠4=180°-∠1=180°-30°=150°
(3)我发现∠1=∠3,∠2=∠4。
【点睛】用量角器量角时,注意看刻度要分清内外圈。解决本题时,要善于利用图中隐藏的特殊角(平角),以及它与各角之间的关系,利用已知角,求出未知角。
18.(22-23四年级上·浙江杭州·期中)下面图中的∠1与∠2是不是相等?说明理由。
【答案】∠1=∠2
见详解
【分析】由图可知,∠1不管是加左边的角还是右边的角,都可以组成一个平角;∠2同样不管是加左边的角还是右边的角,都可以组成一个平角,因此∠1和∠2都等于180°减去旁边的角,据此即可得出结论。
【详解】∠1=∠2,理由如下:
因为∠1+∠3=180°
所以∠1=180°-∠3
因为∠2+∠3=180°
所以∠2=180°-∠3
所以∠1=∠2
【点睛】本题主要考查了学生根据简单的等量代换解答问题的能力,同时也考查了平角的定义。
19.(22-23四年级上·湖北省直辖县级单位·期中)如图所示,已知∠1=35°,求∠2、∠3、∠4的度数。
【答案】55°;55°;125°
【分析】∠1和∠2合起来是一个直角,根据∠1=35°即可求出∠2的度数;∠1和90°和∠3合起来是平角,即为180°,即可求得∠3的度数;∠3和∠4合起来是平角,即为180°,即可求得∠4的度数。
【详解】∠2=180°-90°-35°=55°
∠3=180°-35°-90°=55°
∠4=180°-55°=125°
答:∠2的度数是55°,∠3的度数是55°,∠4的度数是125°。
【点睛】本题考查平角和直角的概念,关键是从图中看到哪些角的和是90度,哪些角的和是180度。
20.(22-23四年级上·山东菏泽·期中)如图,已知,求、、的度数。
【答案】50°;130°;50°
【分析】观察图可知:∠1+∠2=90°,为直角,已知∠1=40°,所以∠2=90°-∠1;∠3+∠2=180°,为平角,所以∠3=180°-∠2;∠3+∠4=180°,为平角,所以∠4=180°-∠3,据此解答即可。
【详解】如图,因为,∠1+∠2=90°所以,∠2=90°-40°=50°;
∠3=180°-50°=130°;
∠4=180°-130°=50°;
答:∠2的度数为50°,∠3的度数为130°,∠4的度数为50°。
【点睛】本题考查角度的计算,掌握理解平角和直角的度是解决本题的关键。
21.(23-24四年级上·河南新乡·期中)∠1和∠2组成一个平角,∠2的度数是∠1的4倍,∠1和∠2各是多少度?
【答案】∠1的度数是36°,∠2的度数是144°。
【分析】∠1和∠2组成一个平角,因此∠1+∠2=180°,又已知∠2的度数是∠1的4倍,即∠2=4∠1,因此∠1+4∠1=180°,利用等式的性质可求出∠1的度数,再用180减去∠1的度数即可得到∠2的度数。
【详解】因为∠1和∠2组成一个平角,所以∠1+∠2=180°;
又因为∠2=4∠1,所以∠1+4∠1=180°,5∠1=180°,∠1=180°÷5=36°;
∠2=180°-36°=144°。
答:∠1的度数是36°,∠2的度数是144°。
【点睛】观察图形得出∠1和∠2组成一个平角,再结合已知条件以及利用平角的定义解决问题。
22.(23-24四年级上·河南南阳·期中)乐乐把两张硬纸条订在一起,组成了一个37°的角,同桌欢欢在乐乐摆的基础上旋转其中一条边,所形成的角的度数比乐乐的4倍还大12°,这个角是多少度?是什么角?
【答案】160°;钝角
【分析】根据题意可知,用乐乐组成角的度数乘4后,再加12°,即可得到欢欢组成角的度数,依此计算并根据角的分类标准解答即可。
【详解】37°×4+12°
=148°+12°
=160°
160°是一个钝角。
答:这个角是160°,是钝角。
23.(23-24四年级上·山东菏泽·期中)测量下面各角的度数,你发现了什么?
∠1=( ),∠2=( ),∠3=( )。
发现:
【答案】92°;46°;46°;
发现:∠2=∠3,∠1=2∠2=2∠3。
【分析】用量角器量角的步骤: 1、把量角器放在角的上面;使量角器的中心和角的顶点重合; 2、零度刻度线和角的一条边重合; 3、角的另一条边所对的量角器上的刻度,就是这个角的度数。据此解答。
【详解】由分析量角得:
∠1=92°,∠2=46°,∠3=46°;
46°×2=92°;
发现:∠2=∠3,∠1=2∠2=2∠3。
24.(23-24四年级上·云南玉溪·期中)已知∠1=25°,求∠2、∠3、∠5各等于多少度。
【答案】155°;25°;65°
【分析】∠1和∠2合起来是平角,即为180°,已知∠1=25°,利用减法即可求得∠2的度数;∠3和∠2合起来是平角,即为180°,利用求得的∠2的度数,即可求得∠3的度数;∠1和∠5合起来是个直角,即为90°,根据∠1=25°即可求得∠5的度数。
【详解】∠1=25°
∠1+∠2=180°
∠2=180°-25°=155°
∠3+∠2=180°
∠3=180°-155°=25°
∠1+∠5=90°
∠5=90°-25°=65°
答:∠2=155°,∠3=25°∠5=65°。
25.(23-24四年级上·江苏宿迁·期末)把一张长方形纸的一个角折起来(如图),已知∠2=130°,则∠1是多少度?
【答案】25°
【分析】把长方形纸折起来的部分展开,可以发现2个∠1加1个∠2等于180°,据此计算即可。
【详解】∠1+∠1+∠2=180°,而∠2=130°,则∠1+∠1=180°-130°=50°,则∠1=50°÷2=25°。
答:∠1是25°。
26.(24-25四年级上·全国·单元测试)有∠1、∠2、∠3三个角,其中∠1的度数最大,∠2比直角小,∠3既不是锐角也不是钝角。这三个角分别可能是什么样的角?
【答案】∠2是锐角,∠3是直角,则∠1是钝角;∠2是锐角,若∠3是平角,则∠1是周角。
【分析】因为比直角小的角是锐角,所以∠2是锐角,因为∠3 既不是锐角也不是钝角,所以∠3可能是直角,也可能是平角;又因为在∠1、∠2、∠3三个角中,∠1的度数最大,所以∠3为直角,∠1为平角,若∠3是平角,则∠1是周角。
【详解】根据分析:∠2是锐角,∠3是直角,则∠1是钝角;∠2是锐角,若∠3是平角,则∠1是周角。
21世纪教育网(www.21cnjy.com)
四年级数学上册专项精练(知识梳理+典例精讲+专项精练)
线段、直线、射线的认识和特征
图形 端点的个数 延长情况 是否可测量
直线 0个 两端无限延长 无法测量
射线 1个 一端可以延长 无法测量
线段 2个 不可延长 可以测量
2、数线段的方法
(1)定义法:从基本线段数起;以某一点为左端点数起。
(2)公式法:
①加法公式:首先数出线段由几个端点,然后从1+2+3+……+(n-1),其中n代表端点数量。
②乘法公式:n×(n-1)÷2(其中n代表端点数量)。
1、角的定义:从一点引出两条射线所组成的图形叫做角。
2、角的各部分名称:这个公共端点叫做角的顶点,这两条射线叫做角的两条边。
3、角的表示方法:角通常用符号“∠”来表示,不同的角可以用数字区分,如∠1、∠2,但要在相应的图中表明。
1、角的计量单位:角的计量单位是“度”,用符号“°”表示。
将半圆(或圆)平均分成180(或360)等份,每一份所对的角的大小就是1度。
2、角的度量工具:量角器是度量角的工具。
3、角的度量方法
(1)把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合;
(2)角的另一边所对的量角器上的刻度,就是这个角的度数。
(3)与量角器0°刻度线重合的边向右,就看里圈的刻度数;相反就看外圈的刻度数。
角的名称 图形 意义 特征
锐角 小于的角叫作锐角。 < 锐角 <
直角 等于的角叫做直角。 直角 =
钝角 大于而小于的角叫作钝角。 < 钝角 <
平角 角的两边成一条直线,这时所形成的角是平角。 平角=
周角 一条射线绕它的顶点旋转一周所形成的角是周角。 周角=
1、锐角<直角<钝角<平角<周角;
2、1平角=2直角,1周角=2平角=4直角。
3、角的性质
角的大小与边的长短无关:角的大小只与两条边叉开的大小有关,叉开得越大,角越大。
放大镜不能放大角:放大镜可以改变物体的大小,但不能改变角的大小。
【典例精讲1】(23-24四年级上·四川乐山·期中)先画第一条长为2厘米的线段,再画第二条线段的长度是第一条线段的5倍。第二条线段长是多少分米?
【答案】画图见详解;1分米
【分析】根据线段的含义,线段有2个端点,有限长,画出一条2厘米的线段,再画第二条线段的长度是第一条线段5倍的线段,即2×5=10厘米的线段,然后根据1分米=10厘米,将厘米换算分米,即可求出第二条线段长是多少分米。
【详解】(1)
(2)2×5=10(厘米)
10厘米=1分米
答:第二条线段长是1分米。
【典例精讲2】(19-20四年级上·湖北十堰·期末)由一点引出的3条射线,可以组成多少个角?由一点引出10条射线,可以组成多少个角?
【答案】3个;45个
【分析】从一点出发引出3条射线,每一条射线都分别与其它的射线组成一个角,所以3条射线就可以组成2+1=3个角;
从一点出发引出10条射线,每一条射线都分别与其它的射线组成一个角,依此可得组成角的个数是9+8+7+6+5+4+3+2+1=45个角。
【详解】2+1=3(个)
9+8+7+6+5+4+3+2+1
=(9+1)×9÷2
=10×9÷2
=90÷2
=45(个)
答:由一点引出的3条射线,可以组成3个角;由一点引出10条射线,可以组成45个角。
【点睛】本题考查了数角的概念,要有总结规律的能力或公式应用的能力。
【典例精讲3】(23-24四年级上·山西晋中·期中)小华在使用量角器测量∠1时,用量角器的0刻度线与∠1的一条边重合,然后顺着0刻度线向上看,∠1的另一边对着125°这条刻度线。小红在测量∠2时,用量角器10°刻度线与∠2的一条边重合,然后顺着10°刻度线向上看,∠2的另一条边对准130°这条刻度线,两人读数都正确,你能判断∠1和∠2两个角哪个角大,哪个角小吗?
【答案】∠1大;∠2小
【分析】量角的步骤是:先把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合,角的另一边所对的量角器上的刻度,就是这个角的度数,依此计算出∠1的度数;然后用130°减10°,从而计算出∠2的度数,最后再比较即可。
【详解】根据题意可知,∠1=125°。
∠2=130°-10°=120°
125°>120°
答:∠1大,∠2小。
【典例精讲4】(22-23四年级上·江西吉安·期末)下面是一张长方形纸折起来以后形成的图形,已知:∠1和一个145°的角正好可拼成一个平角,求∠1和∠2的度数。
【答案】∠1=35°;∠2=20°
【分析】1直角=90°,1平角=180°,根据题意可知:∠1+145°=180°,因此∠1=180°-145°;∠1+∠1+∠2=90°,因此用90°减去2个∠1即可得到∠2的度数,依此计算。
【详解】∠1=180°-145°=35°;
35°+35°=70°
90°-70°=20°
答:∠1=35°,∠2=20°。
【点睛】此题考查的是角的分类与换算,熟练掌握平角、直角的特点是解答此题的关键。
【典例精讲5】(23-24四年级上·河南新乡·期中)一个平角由两个角拼成,其中一个角是45度,另一个角是多少度?
【答案】135度
【分析】平角等于180度,因此用180度减去其中一个角的度数,即可计算出另一个角的度数;据此解答。
【详解】180-45=135(度)
答:另一个角是135度。
学校:___________ 姓名:___________ 班级:___________
解答题
1.(23-24四年级上·广东佛山·期末)张叔叔是个台球迷,他发现当台球撞击桌边时就会向另一个方向弹走,如图所示:
(1)已知∠1=45°,∠3=50°,请你量一量,∠2=( ),∠4=( )。
(2)如上图,台球撞向桌边的路线与桌边形成了一个角,它弹走的路线与桌边也形成了一个角,你发现( )。
(3)请运用你发现的规律在上面图3中画出台球向另一个方向弹走的角度和路线。
2.(23-24四年级上·四川·期中)两个正方形相交如下图,∠2大小未知,∠1与∠3相等吗?
3.(23-24四年级上·全国·单元测试)下图是一张长方形纸折起来后的图形,已知∠1=50°,求∠2的度数。
4.(22-23四年级上·广东揭阳·期中)已知∠1=32°,∠2=38°,求∠3的度数。
5.(23-24四年级上·陕西咸阳·期中)如图,欢欢要从家出发去奇奇家玩。最短的路线是几号?为什么?
6.(23-24四年级上·云南昆明·期中)已知∠3=60°,∠5=30°。求∠1、∠2、∠4的度数。
7.(23-24四年级上·湖南怀化·期末)如图:已知∠1=50°,求∠2的度数。
8.(23-24四年级上·河南信阳·期末)将一副三角板中的两块直角三角尺按下图两种方式摆放。
(1)求图1中∠1和∠2的度数。
(图1)
(2)猜想图2中∠1和∠2的数量关系,通过计算说明理由。
(图2)
9.(22-23四年级上·河南驻马店·期末)两只蚂蚁夺旗,它们的位置如图所示。
10.(23-24四年级上·河北邯郸·期末)红星小学位于劳动路与南山大道的交叉口,下图是红星小学的位置示意图。
(1)用量角器量出∠1=( )°。
(2)张师傅要给红星小学送纯净水,请你为张师傅设计一条最近的路。
11.(23-24四年级上·全国·单元测试)如下图,∠2是∠1的2倍,∠3是∠1的6倍,求∠1、∠2和∠3的度数。
12.(23-24四年级上·安徽黄山·期末)在下图中按要求画图,并解决问题。
(1)画出直线AB。
(2)画出射线BC。
(3)画好的图形中有( )种角。在图中指出并写出角的名称。
13.(22-23四年级上·全国·课后作业)小乐用一副三角尺在一块长方形纸板上拼出了下面的图形(图中的阴影部分),爸爸说∠1=30°,请求出∠2的度数。
14.(22-23四年级上·河南洛阳·期末)用量角器量一量下面的角,再比一比,说说自己的发现。
我发现:( )。
15.(22-23四年级上·北京·单元测试)如果两条平行线被一条直线所截(如图),会产生很多个有联系的角。
(1)请用量角器测量∠1、∠2,你发现了什么?
(2)根据上面得到的结论,观察∠3、∠5,通过推理说明∠3和∠5的关系。
16.(22-23四年级上·广东广州·期末)如图,在长方形ABCD中已知∠1=80°,∠5=40°。分别求出∠2、∠3和∠6的度数。
17.(22-23四年级上·辽宁抚顺·期末)按要求完成下列内容。
(1)量出∠1=( )°。
(2)求出∠2、∠3、∠4的度数。
(3)你发现了什么?
18.(22-23四年级上·浙江杭州·期中)下面图中的∠1与∠2是不是相等?说明理由。
19.(22-23四年级上·湖北省直辖县级单位·期中)如图所示,已知∠1=35°,求∠2、∠3、∠4的度数。
20.(22-23四年级上·山东菏泽·期中)如图,已知,求、、的度数。
21.(23-24四年级上·河南新乡·期中)∠1和∠2组成一个平角,∠2的度数是∠1的4倍,∠1和∠2各是多少度?
22.(23-24四年级上·河南南阳·期中)乐乐把两张硬纸条订在一起,组成了一个37°的角,同桌欢欢在乐乐摆的基础上旋转其中一条边,所形成的角的度数比乐乐的4倍还大12°,这个角是多少度?是什么角?
23.(23-24四年级上·山东菏泽·期中)测量下面各角的度数,你发现了什么?
∠1=( ),∠2=( ),∠3=( )。
发现:
24.(23-24四年级上·云南玉溪·期中)已知∠1=25°,求∠2、∠3、∠5各等于多少度。
25.(23-24四年级上·江苏宿迁·期末)把一张长方形纸的一个角折起来(如图),已知∠2=130°,则∠1是多少度?
26.(24-25四年级上·全国·单元测试)有∠1、∠2、∠3三个角,其中∠1的度数最大,∠2比直角小,∠3既不是锐角也不是钝角。这三个角分别可能是什么样的角?
21世纪教育网(www.21cnjy.com)
第三单元 《角的度量》 单元复习讲义(讲义)
四年级数学上册专项精练(知识梳理+典例精讲+专项精练)
线段、直线、射线的认识和特征
图形 端点的个数 延长情况 是否可测量
直线 0个 两端无限延长 无法测量
射线 1个 一端可以延长 无法测量
线段 2个 不可延长 可以测量
2、数线段的方法
(1)定义法:从基本线段数起;以某一点为左端点数起。
(2)公式法:
①加法公式:首先数出线段由几个端点,然后从1+2+3+……+(n-1),其中n代表端点数量。
②乘法公式:n×(n-1)÷2(其中n代表端点数量)。
1、角的定义:从一点引出两条射线所组成的图形叫做角。
2、角的各部分名称:这个公共端点叫做角的顶点,这两条射线叫做角的两条边。
3、角的表示方法:角通常用符号“∠”来表示,不同的角可以用数字区分,如∠1、∠2,但要在相应的图中表明。
1、角的计量单位:角的计量单位是“度”,用符号“°”表示。
将半圆(或圆)平均分成180(或360)等份,每一份所对的角的大小就是1度。
2、角的度量工具:量角器是度量角的工具。
3、角的度量方法
(1)把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合;
(2)角的另一边所对的量角器上的刻度,就是这个角的度数。
(3)与量角器0°刻度线重合的边向右,就看里圈的刻度数;相反就看外圈的刻度数。
角的名称 图形 意义 特征
锐角 小于的角叫作锐角。 < 锐角 <
直角 等于的角叫做直角。 直角 =
钝角 大于而小于的角叫作钝角。 < 钝角 <
平角 角的两边成一条直线,这时所形成的角是平角。 平角=
周角 一条射线绕它的顶点旋转一周所形成的角是周角。 周角=
1、锐角<直角<钝角<平角<周角;
2、1平角=2直角,1周角=2平角=4直角。
3、角的性质
角的大小与边的长短无关:角的大小只与两条边叉开的大小有关,叉开得越大,角越大。
放大镜不能放大角:放大镜可以改变物体的大小,但不能改变角的大小。
【典例精讲1】(23-24四年级上·四川乐山·期中)先画第一条长为2厘米的线段,再画第二条线段的长度是第一条线段的5倍。第二条线段长是多少分米?
【答案】画图见详解;1分米
【分析】根据线段的含义,线段有2个端点,有限长,画出一条2厘米的线段,再画第二条线段的长度是第一条线段5倍的线段,即2×5=10厘米的线段,然后根据1分米=10厘米,将厘米换算分米,即可求出第二条线段长是多少分米。
【详解】(1)
(2)2×5=10(厘米)
10厘米=1分米
答:第二条线段长是1分米。
【典例精讲2】(19-20四年级上·湖北十堰·期末)由一点引出的3条射线,可以组成多少个角?由一点引出10条射线,可以组成多少个角?
【答案】3个;45个
【分析】从一点出发引出3条射线,每一条射线都分别与其它的射线组成一个角,所以3条射线就可以组成2+1=3个角;
从一点出发引出10条射线,每一条射线都分别与其它的射线组成一个角,依此可得组成角的个数是9+8+7+6+5+4+3+2+1=45个角。
【详解】2+1=3(个)
9+8+7+6+5+4+3+2+1
=(9+1)×9÷2
=10×9÷2
=90÷2
=45(个)
答:由一点引出的3条射线,可以组成3个角;由一点引出10条射线,可以组成45个角。
【点睛】本题考查了数角的概念,要有总结规律的能力或公式应用的能力。
【典例精讲3】(23-24四年级上·山西晋中·期中)小华在使用量角器测量∠1时,用量角器的0刻度线与∠1的一条边重合,然后顺着0刻度线向上看,∠1的另一边对着125°这条刻度线。小红在测量∠2时,用量角器10°刻度线与∠2的一条边重合,然后顺着10°刻度线向上看,∠2的另一条边对准130°这条刻度线,两人读数都正确,你能判断∠1和∠2两个角哪个角大,哪个角小吗?
【答案】∠1大;∠2小
【分析】量角的步骤是:先把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合,角的另一边所对的量角器上的刻度,就是这个角的度数,依此计算出∠1的度数;然后用130°减10°,从而计算出∠2的度数,最后再比较即可。
【详解】根据题意可知,∠1=125°。
∠2=130°-10°=120°
125°>120°
答:∠1大,∠2小。
【典例精讲4】(22-23四年级上·江西吉安·期末)下面是一张长方形纸折起来以后形成的图形,已知:∠1和一个145°的角正好可拼成一个平角,求∠1和∠2的度数。
【答案】∠1=35°;∠2=20°
【分析】1直角=90°,1平角=180°,根据题意可知:∠1+145°=180°,因此∠1=180°-145°;∠1+∠1+∠2=90°,因此用90°减去2个∠1即可得到∠2的度数,依此计算。
【详解】∠1=180°-145°=35°;
35°+35°=70°
90°-70°=20°
答:∠1=35°,∠2=20°。
【点睛】此题考查的是角的分类与换算,熟练掌握平角、直角的特点是解答此题的关键。
【典例精讲5】(23-24四年级上·河南新乡·期中)一个平角由两个角拼成,其中一个角是45度,另一个角是多少度?
【答案】135度
【分析】平角等于180度,因此用180度减去其中一个角的度数,即可计算出另一个角的度数;据此解答。
【详解】180-45=135(度)
答:另一个角是135度。
学校:___________ 姓名:___________ 班级:___________
解答题
1.(23-24四年级上·广东佛山·期末)张叔叔是个台球迷,他发现当台球撞击桌边时就会向另一个方向弹走,如图所示:
(1)已知∠1=45°,∠3=50°,请你量一量,∠2=( ),∠4=( )。
(2)如上图,台球撞向桌边的路线与桌边形成了一个角,它弹走的路线与桌边也形成了一个角,你发现( )。
(3)请运用你发现的规律在上面图3中画出台球向另一个方向弹走的角度和路线。
【答案】(1)45°;50°
(2)这两个角相等
(3)见详解
【分析】(1)量角器可以分别量出∠2、∠4的度数(把量角器的中心与角的顶点重合,刻度线与边的一边重合,角的另一边所经过的量角器上所显示的刻度就是被量角的度数)。
(2)根据量出的各角度数,台球撞向桌边的路线与桌边形成了一个角,它弹走的路线也与桌边形成了一个角,两个角度数相同,据此解答。
(3)根据以上发现,即可完成如图的台球运动线路图。
【详解】(1)已知∠1=45°,∠3=50°,经测量∠2=45°,∠4=50°。
台球撞向桌边的路线与桌边形成了一个角,它弹走的路线与桌边也形成了一个角,发现这两个角相等。
(3)如图:
2.(23-24四年级上·四川·期中)两个正方形相交如下图,∠2大小未知,∠1与∠3相等吗?
【答案】∠1与∠3相等
【分析】观察图形可得∠1+∠2=90°,∠3+∠2=90°,分别表示出∠1和∠3的大小,比较即可得出答案。
【详解】观察图形可得∠1+∠2=90°,∠3+∠2=90°,
所以∠1=90°-∠2,∠3=90°-∠2,
即∠1=∠3,
答:∠1与∠3相等
【点睛】本题的关键是熟练掌握角度的计算。
3.(23-24四年级上·全国·单元测试)下图是一张长方形纸折起来后的图形,已知∠1=50°,求∠2的度数。
【答案】65°
【分析】由对折的性质可知,∠2挡住的角就等于∠2,因为三个角的度数和是平角,平角=180°,∠1=50°,所以180°-50°=130°,∠2=130°÷2=65°。
【详解】(180°-50°)÷2
=130°÷2
=65°
答:∠2的度数是65°。
4.(22-23四年级上·广东揭阳·期中)已知∠1=32°,∠2=38°,求∠3的度数。
【答案】110°
【分析】根据题图可知,∠1、∠2和∠3组成一个平角,则∠3=180°-∠2-∠1。
【详解】∠3=180°-∠2-∠1=180°-38°-32°=110°
答:∠3的度数是110°。
【点睛】解决此类问题时,要善于利用图中隐藏的特殊角(直角、平角、周角),以及它与各角之间的关系,利用已知角,求出未知角。
5.(23-24四年级上·陕西咸阳·期中)如图,欢欢要从家出发去奇奇家玩。最短的路线是几号?为什么?
【答案】③;两点之间的所有连线中,线段最短。
【分析】根据线段的定义及特征可知,两点之间的所有连线中,线段最短,据此解答即可。
【详解】欢欢要从家出发去奇奇家玩的五条路中,只有③是线段,而两点之间,线段最短。即可得出答案。
6.(23-24四年级上·云南昆明·期中)已知∠3=60°,∠5=30°。求∠1、∠2、∠4的度数。
【答案】60°;120°;90°
【分析】用平角的度数减去∠3和∠5的度数,即可求出∠4的度数,再用平角的度数减去∠3的度数,即可求出∠2的度数,用平角的度数减去∠2的度数,即可求出∠1的度数,代入数据计算。
【详解】∠2=180°-60°=120°
∠1=180°-120°=60°
∠4=180°-60°-30°=90°
答:∠1的度数是60°,∠2的度数是120°,∠4的度数是90°。
7.(23-24四年级上·湖南怀化·期末)如图:已知∠1=50°,求∠2的度数。
【答案】80°
【分析】将长方形纸折起一部分,则折起后的∠1与折起前的角的度数是相同的,都是50°,又这三个角组成了一个平角,据此即可求出∠2的度数。
【详解】结合分析可知,由于∠2与另外两个角组成了一个平角,平角的度数是180°,故∠2=180°-50°-50°=80°。
8.(23-24四年级上·河南信阳·期末)将一副三角板中的两块直角三角尺按下图两种方式摆放。
(1)求图1中∠1和∠2的度数。
(图1)
(2)猜想图2中∠1和∠2的数量关系,通过计算说明理由。
(图2)
【答案】(1)∠1=120°;∠2=135°
(2)∠1=∠2。
在含有45°三角尺中,∠1+∠3=90°,在含有30°的三角尺中,∠2+∠3=90°;
所以∠1+∠3=∠2+∠3=90°,则∠1=∠2。
【分析】(1)根据图中哪两个角组成平角,利用平角减去已知角来依次计算出所要求的角的度数。平角是等于180°的角,已知三角尺中的60°角和∠1形成平角,用平角减去60°,即可求出∠1的度数,三角板中的45°角和∠2形成平角,用平角减去45°,即可求出∠2的度数。
(2)两个三角板都有一个直角,∠1+∠3=90°,∠2+∠3=90°,∠3重合,∠1=∠2。
【详解】(1)∠1=180°-60°=120°,∠2=180°-45°=135°
(2)∠1=∠2。
在含有45°三角尺中,∠1+∠3=90°,在含有30°的三角尺中,∠2+∠3=90°
所以∠1+∠3=∠2+∠3=90°,则∠1=∠2。
9.(22-23四年级上·河南驻马店·期末)两只蚂蚁夺旗,它们的位置如图所示。
【答案】不公平,因为乙蚂蚁与旗的距离短一些。
【分析】甲、乙两只蚂蚁夺旗,要想游戏规则公平,甲、乙蚂蚁与旗的距离必须相等,由图可知距离长短,据此解答。
【详解】答:由图可以看出,不公平,因为乙蚂蚁与旗的距离短一些。
10.(23-24四年级上·河北邯郸·期末)红星小学位于劳动路与南山大道的交叉口,下图是红星小学的位置示意图。
(1)用量角器量出∠1=( )°。
(2)张师傅要给红星小学送纯净水,请你为张师傅设计一条最近的路。
【答案】(1)130
(2)见详解
【分析】(1)量角器的中心与角的顶点重合,0刻度线与角的一边重合,角的另一边所对的量角器上的刻度,就是这个角的度数;用量角器量出∠1的度数即可解答。
(2)两点之间线段最短,沿纯净水站到红星小学的线段走最近,据此画出即可解答。
【详解】(1)经测量,∠1=130°。
(2)
11.(23-24四年级上·全国·单元测试)如下图,∠2是∠1的2倍,∠3是∠1的6倍,求∠1、∠2和∠3的度数。
【答案】∠1=20°;∠2=40°;∠3=120°
【分析】根据题意,∠2和∠3都以∠1为标准量,所以把∠1的度数看作1份,则∠2就是2份,∠3就是6份;一共就是(1+2+6)份;从图中可以看出,三个角组成了平角,总度数为180°,所以用总度数180°除以总份数,得到其中一份的度数,即∠1的度数,再用∠1的度数分别乘2和6,即得到∠2和∠3的度数。据此解答。
【详解】180°÷(1+2+6)
=180°÷(3+6)
=180°÷9
=20°
20°×2=40°
20°×6=120°
所以,∠1=20°;∠2=40°;∠3=120°。
12.(23-24四年级上·安徽黄山·期末)在下图中按要求画图,并解决问题。
(1)画出直线AB。
(2)画出射线BC。
(3)画好的图形中有( )种角。在图中指出并写出角的名称。
【答案】(1)见详解
(2)见详解
(3)3;见详解
【分析】(1)过点A、点B画一条直的线即可;
(2)以点B为端点,过点C画一条直的线即可;
(3)两条边在一条直线上的角是平角,小于90°的角是锐角,大于90°小于180°的角是钝角;根据(1)和(2)画出的图可以看出,以A点为顶点的角是平角,∠CBA为锐角,与∠CBA有公共边BC,且与∠CBA组成平角的角是钝角,所以图形中有3种角,据此即可解答。
【详解】(1)(2)见下图:
(3)画好的图形中有3种角。图见(1)(2)。
13.(22-23四年级上·全国·课后作业)小乐用一副三角尺在一块长方形纸板上拼出了下面的图形(图中的阴影部分),爸爸说∠1=30°,请求出∠2的度数。
【答案】45°
【分析】根据题图可知,∠1、∠2和三角尺中60°、45°的角组成一个平角,则∠2=180°-∠1-60°-45°。
【详解】∠2=180°-∠1-60°-45°=180°-30°-60°-45°=45°
【点睛】解决此类问题时,要善于利用图中隐藏的特殊角(直角、平角、周角)、三角尺中各个角,以及它与各角之间的关系,利用已知角,求出未知角。
14.(22-23四年级上·河南洛阳·期末)用量角器量一量下面的角,再比一比,说说自己的发现。
我发现:( )。
【答案】40°;40°;40°
角的大小与边的长短无关,只与两边张开的程度有关。
【分析】量角的步骤:先把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合。再看角的另一边所对的量角器上的刻度,就是这个角的度数。据此量出三个角的度数,再进行解答。
【详解】这三个角的度数分别是40°、40°、40°,度数相等,但是角的两条边的长度不相等,说明角的大小与边的长短无关,只与两边张开的程度有关。
【点睛】本题考查用量角器测量角的度数的方法以及角的认识,角两边张开程度不变,边的长度改变,角的大小不变。
15.(22-23四年级上·北京·单元测试)如果两条平行线被一条直线所截(如图),会产生很多个有联系的角。
(1)请用量角器测量∠1、∠2,你发现了什么?
(2)根据上面得到的结论,观察∠3、∠5,通过推理说明∠3和∠5的关系。
【答案】(1)∠1=∠2
(2)∠3=∠5
【分析】(1)分别量出∠1、∠2的度数,再比较大小即可;
(2)平角=180°,∠1加∠3为平角,∠2加∠5为平角,根据平角的定义,再判断∠3、∠5的大小关系即可;据此解答。
【详解】(1)∠1=150°,∠2=150°
所以∠1=∠2。
答:我发现了∠1=∠2。
(2)因为∠1+∠3=180°,∠2+∠5=180°
又因为∠1=∠2,所以∠3=∠5。
答:∠3=∠5。
【点睛】能熟练用量角器量角的度数,是解答此题的关键。
16.(22-23四年级上·广东广州·期末)如图,在长方形ABCD中已知∠1=80°,∠5=40°。分别求出∠2、∠3和∠6的度数。
【答案】100°;80°;50°
【分析】∠1和∠2组成平角,平角是180°,∠2=180°-∠1;
∠2和∠3组成平角,平角是180°,∠3=180°-∠2;
长方形的四个角是直角为90°,∠6=90°-∠5,依此解答即可。
【详解】因为∠1=80°,所以,∠2=180°-80°=100°;
∠3=180°-∠2=180°-100°=80°;
因为∠5=40°,所以,∠6=90°-40°=50°;
答:∠2=100°;∠3=80°;∠6=50°。
【点睛】明白平角和直角的度数,找到对应组成的角是解题关键。
17.(22-23四年级上·辽宁抚顺·期末)按要求完成下列内容。
(1)量出∠1=( )°。
(2)求出∠2、∠3、∠4的度数。
(3)你发现了什么?
【答案】(1)30
(2)∠2=150°;∠3=30°;∠4=150°
(3)∠1=∠3,∠2=∠4
【分析】(1)量角的步骤:先把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合。再看角的另一边所对的量角器上的刻度,就是这个角的度数。
(2)∠1和∠2组成一个平角,则∠2=180°-∠1。∠3和∠2组成一个平角,则∠3=180°-∠2。∠1和∠4组成一个平角,则∠4=180°-∠1。
(3)这四个角中,∠1=∠3,∠2=∠4。
【详解】(1)量出∠1=30°。
(2)∠2=180°-∠1=180°-30°=150°
∠3=180°-∠2=180°-150°=30°
∠4=180°-∠1=180°-30°=150°
(3)我发现∠1=∠3,∠2=∠4。
【点睛】用量角器量角时,注意看刻度要分清内外圈。解决本题时,要善于利用图中隐藏的特殊角(平角),以及它与各角之间的关系,利用已知角,求出未知角。
18.(22-23四年级上·浙江杭州·期中)下面图中的∠1与∠2是不是相等?说明理由。
【答案】∠1=∠2
见详解
【分析】由图可知,∠1不管是加左边的角还是右边的角,都可以组成一个平角;∠2同样不管是加左边的角还是右边的角,都可以组成一个平角,因此∠1和∠2都等于180°减去旁边的角,据此即可得出结论。
【详解】∠1=∠2,理由如下:
因为∠1+∠3=180°
所以∠1=180°-∠3
因为∠2+∠3=180°
所以∠2=180°-∠3
所以∠1=∠2
【点睛】本题主要考查了学生根据简单的等量代换解答问题的能力,同时也考查了平角的定义。
19.(22-23四年级上·湖北省直辖县级单位·期中)如图所示,已知∠1=35°,求∠2、∠3、∠4的度数。
【答案】55°;55°;125°
【分析】∠1和∠2合起来是一个直角,根据∠1=35°即可求出∠2的度数;∠1和90°和∠3合起来是平角,即为180°,即可求得∠3的度数;∠3和∠4合起来是平角,即为180°,即可求得∠4的度数。
【详解】∠2=180°-90°-35°=55°
∠3=180°-35°-90°=55°
∠4=180°-55°=125°
答:∠2的度数是55°,∠3的度数是55°,∠4的度数是125°。
【点睛】本题考查平角和直角的概念,关键是从图中看到哪些角的和是90度,哪些角的和是180度。
20.(22-23四年级上·山东菏泽·期中)如图,已知,求、、的度数。
【答案】50°;130°;50°
【分析】观察图可知:∠1+∠2=90°,为直角,已知∠1=40°,所以∠2=90°-∠1;∠3+∠2=180°,为平角,所以∠3=180°-∠2;∠3+∠4=180°,为平角,所以∠4=180°-∠3,据此解答即可。
【详解】如图,因为,∠1+∠2=90°所以,∠2=90°-40°=50°;
∠3=180°-50°=130°;
∠4=180°-130°=50°;
答:∠2的度数为50°,∠3的度数为130°,∠4的度数为50°。
【点睛】本题考查角度的计算,掌握理解平角和直角的度是解决本题的关键。
21.(23-24四年级上·河南新乡·期中)∠1和∠2组成一个平角,∠2的度数是∠1的4倍,∠1和∠2各是多少度?
【答案】∠1的度数是36°,∠2的度数是144°。
【分析】∠1和∠2组成一个平角,因此∠1+∠2=180°,又已知∠2的度数是∠1的4倍,即∠2=4∠1,因此∠1+4∠1=180°,利用等式的性质可求出∠1的度数,再用180减去∠1的度数即可得到∠2的度数。
【详解】因为∠1和∠2组成一个平角,所以∠1+∠2=180°;
又因为∠2=4∠1,所以∠1+4∠1=180°,5∠1=180°,∠1=180°÷5=36°;
∠2=180°-36°=144°。
答:∠1的度数是36°,∠2的度数是144°。
【点睛】观察图形得出∠1和∠2组成一个平角,再结合已知条件以及利用平角的定义解决问题。
22.(23-24四年级上·河南南阳·期中)乐乐把两张硬纸条订在一起,组成了一个37°的角,同桌欢欢在乐乐摆的基础上旋转其中一条边,所形成的角的度数比乐乐的4倍还大12°,这个角是多少度?是什么角?
【答案】160°;钝角
【分析】根据题意可知,用乐乐组成角的度数乘4后,再加12°,即可得到欢欢组成角的度数,依此计算并根据角的分类标准解答即可。
【详解】37°×4+12°
=148°+12°
=160°
160°是一个钝角。
答:这个角是160°,是钝角。
23.(23-24四年级上·山东菏泽·期中)测量下面各角的度数,你发现了什么?
∠1=( ),∠2=( ),∠3=( )。
发现:
【答案】92°;46°;46°;
发现:∠2=∠3,∠1=2∠2=2∠3。
【分析】用量角器量角的步骤: 1、把量角器放在角的上面;使量角器的中心和角的顶点重合; 2、零度刻度线和角的一条边重合; 3、角的另一条边所对的量角器上的刻度,就是这个角的度数。据此解答。
【详解】由分析量角得:
∠1=92°,∠2=46°,∠3=46°;
46°×2=92°;
发现:∠2=∠3,∠1=2∠2=2∠3。
24.(23-24四年级上·云南玉溪·期中)已知∠1=25°,求∠2、∠3、∠5各等于多少度。
【答案】155°;25°;65°
【分析】∠1和∠2合起来是平角,即为180°,已知∠1=25°,利用减法即可求得∠2的度数;∠3和∠2合起来是平角,即为180°,利用求得的∠2的度数,即可求得∠3的度数;∠1和∠5合起来是个直角,即为90°,根据∠1=25°即可求得∠5的度数。
【详解】∠1=25°
∠1+∠2=180°
∠2=180°-25°=155°
∠3+∠2=180°
∠3=180°-155°=25°
∠1+∠5=90°
∠5=90°-25°=65°
答:∠2=155°,∠3=25°∠5=65°。
25.(23-24四年级上·江苏宿迁·期末)把一张长方形纸的一个角折起来(如图),已知∠2=130°,则∠1是多少度?
【答案】25°
【分析】把长方形纸折起来的部分展开,可以发现2个∠1加1个∠2等于180°,据此计算即可。
【详解】∠1+∠1+∠2=180°,而∠2=130°,则∠1+∠1=180°-130°=50°,则∠1=50°÷2=25°。
答:∠1是25°。
26.(24-25四年级上·全国·单元测试)有∠1、∠2、∠3三个角,其中∠1的度数最大,∠2比直角小,∠3既不是锐角也不是钝角。这三个角分别可能是什么样的角?
【答案】∠2是锐角,∠3是直角,则∠1是钝角;∠2是锐角,若∠3是平角,则∠1是周角。
【分析】因为比直角小的角是锐角,所以∠2是锐角,因为∠3 既不是锐角也不是钝角,所以∠3可能是直角,也可能是平角;又因为在∠1、∠2、∠3三个角中,∠1的度数最大,所以∠3为直角,∠1为平角,若∠3是平角,则∠1是周角。
【详解】根据分析:∠2是锐角,∠3是直角,则∠1是钝角;∠2是锐角,若∠3是平角,则∠1是周角。
21世纪教育网(www.21cnjy.com)
