第三单元《角的度量》(计算题篇二大题型)单元复习讲义(知识梳理+典例精讲+专项精练)2024-2025学年四年级数学上册(人教版)(学生版+解析)
文档属性
| 名称 | 第三单元《角的度量》(计算题篇二大题型)单元复习讲义(知识梳理+典例精讲+专项精练)2024-2025学年四年级数学上册(人教版)(学生版+解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-18 00:00:00 | ||
图片预览




文档简介
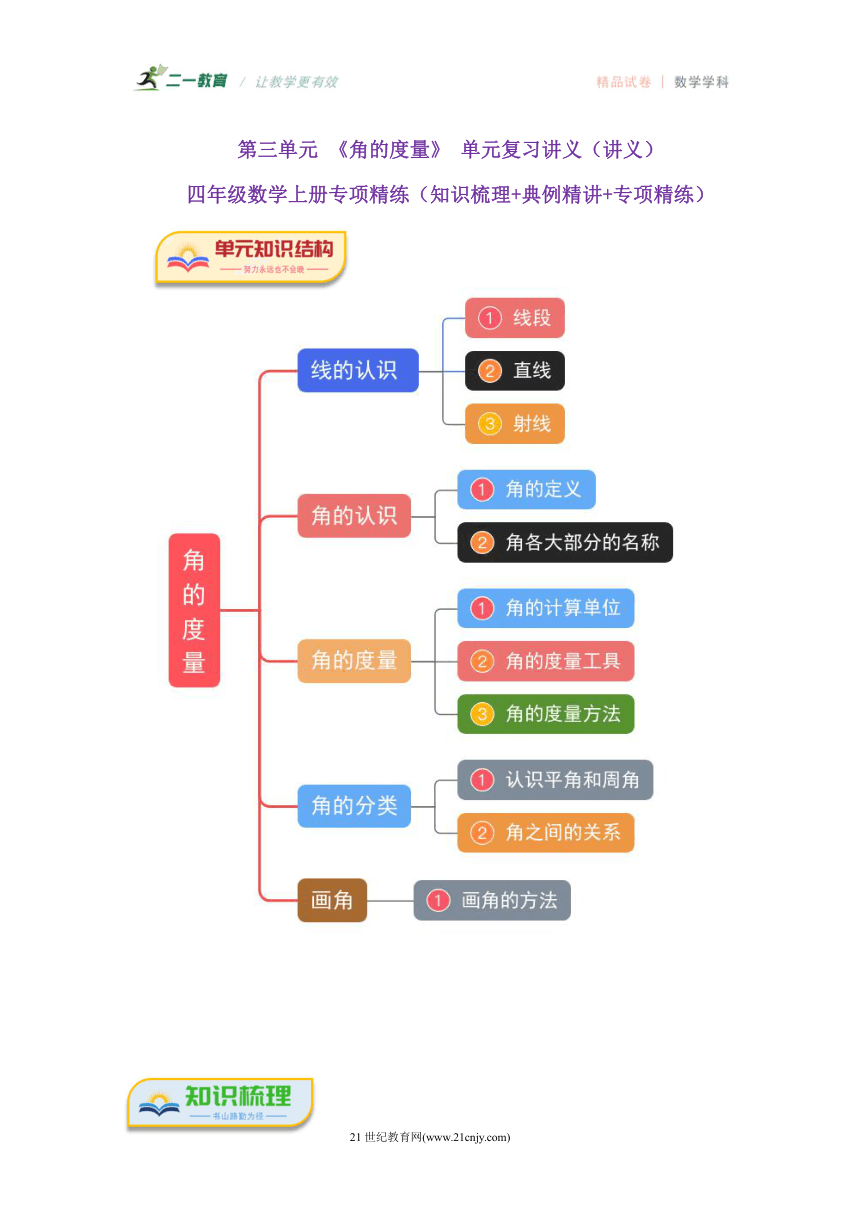
第三单元 《角的度量》 单元复习讲义(讲义)
四年级数学上册专项精练(知识梳理+典例精讲+专项精练)
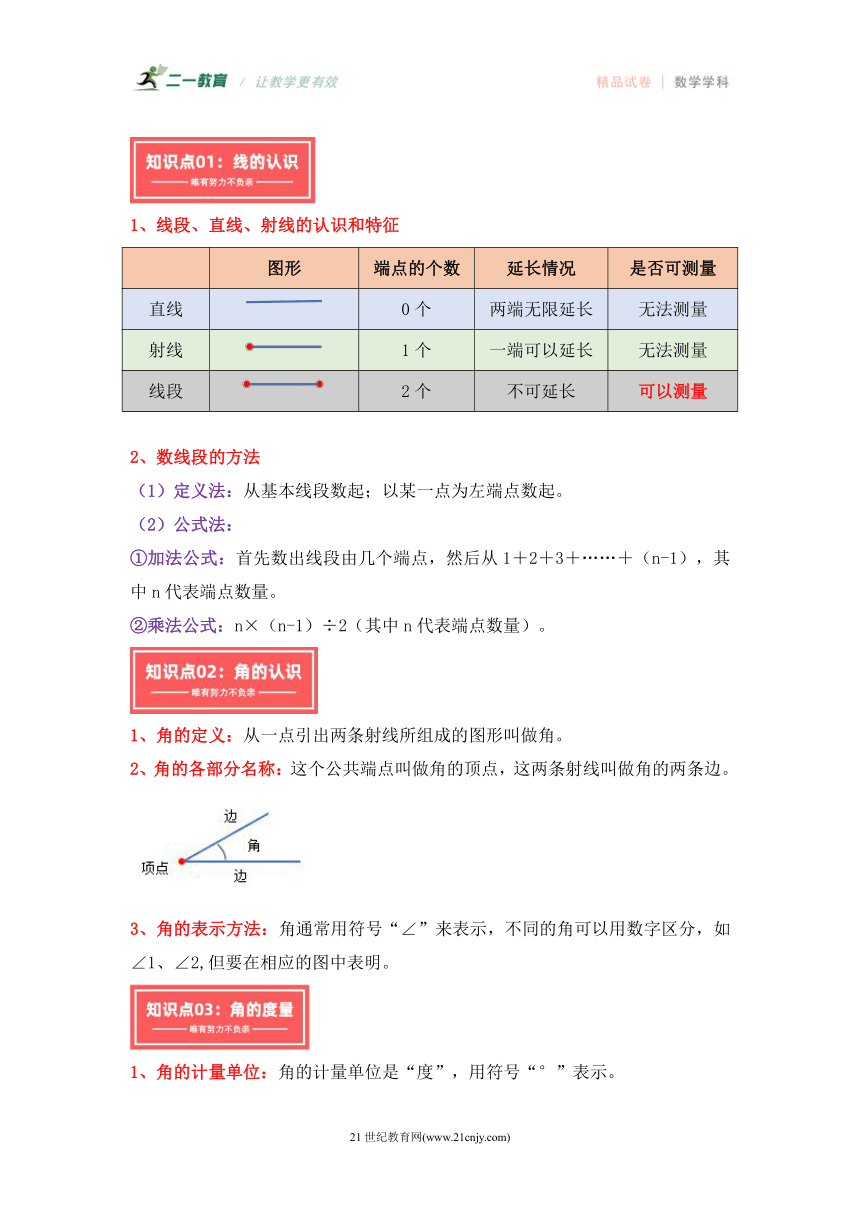
线段、直线、射线的认识和特征
图形 端点的个数 延长情况 是否可测量
直线 0个 两端无限延长 无法测量
射线 1个 一端可以延长 无法测量
线段 2个 不可延长 可以测量
2、数线段的方法
(1)定义法:从基本线段数起;以某一点为左端点数起。
(2)公式法:
①加法公式:首先数出线段由几个端点,然后从1+2+3+……+(n-1),其中n代表端点数量。
②乘法公式:n×(n-1)÷2(其中n代表端点数量)。
1、角的定义:从一点引出两条射线所组成的图形叫做角。
2、角的各部分名称:这个公共端点叫做角的顶点,这两条射线叫做角的两条边。
3、角的表示方法:角通常用符号“∠”来表示,不同的角可以用数字区分,如∠1、∠2,但要在相应的图中表明。
1、角的计量单位:角的计量单位是“度”,用符号“°”表示。
将半圆(或圆)平均分成180(或360)等份,每一份所对的角的大小就是1度。
2、角的度量工具:量角器是度量角的工具。
3、角的度量方法
(1)把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合;
(2)角的另一边所对的量角器上的刻度,就是这个角的度数。
(3)与量角器0°刻度线重合的边向右,就看里圈的刻度数;相反就看外圈的刻度数。
角的名称 图形 意义 特征
锐角 小于的角叫作锐角。 < 锐角 <
直角 等于的角叫做直角。 直角 =
钝角 大于而小于的角叫作钝角。 < 钝角 <
平角 角的两边成一条直线,这时所形成的角是平角。 平角 =
周角 一条射线绕它的顶点旋转一周所形成的角是周角。 周角 =
1、锐角<直角<钝角<平角<周角;
2、1平角=2直角,1周角=2平角=4直角。
3、角的性质
角的大小与边的长短无关:角的大小只与两条边叉开的大小有关,叉开得越大,角越大。
放大镜不能放大角:放大镜可以改变物体的大小,但不能改变角的大小。
【典例精讲1】(四年级上·河南周口·期中)下图是一张长方形纸折起来以后的图形,如果∠2=70°
那么∠1=?
【答案】∠1=40°
【分析】如图,∠1+∠2+∠3=180°,由∠2=70°,得出180°-(∠2+∠3)=∠1,由对折可知∠3=∠2,进一步求得∠1即可。
【详解】∠1=180°-70°×2
=180°-140°
=40°
答:∠1是40°。
【点睛】此题考查利用对折重叠的两个角相等和平角等于180°来解决有关角度计算的问题。
【典例精讲2】(23-24四年级上·河北衡水·期末)如图,两张同样的长方形纸重叠了一部分,已知∠1=55°,分别求出∠2、∠3的度数。
【答案】∠2=35°,∠3=55°
【分析】根据图形,∠1+∠2=90°,因为∠1=55°,所以可以求出∠2的度数;又根据∠3+∠2=90°,继而可求出∠3度数,据此即可解答。
【详解】∠1+∠2=90°,∠1=55°,∠2=90°-55°=35°;
∠2+∠3=90°,所以∠3=90°-35°=55°
【典例精讲3】(22-23四年级上·江西宜春·期末)求出下面各角的度数。
已知如图中∠2=65°,求∠1。
【答案】50°
【分析】由图可知∠2+∠2+∠1=平角,平角为180°,所以∠1=180°-∠2-∠2;据此解答。
【详解】∠1=180°-65°-65°=50°
所以∠1为50°。
学校:___________ 姓名:___________ 班级:___________
计算题
1.(22-23四年级上·河南三门峡·期末)两个正方形叠放在一起,如图,求的度数。
2.(22-23四年级上·湖北孝感·期中)已知∠1=40°,∠5是直角,求∠2、∠3、∠4的度数。
3.(23-24四年级上·湖南郴州·期中)如图,已知∠1=30°,求∠2的度数。
4.(22-23四年级上·黑龙江鸡西·期末)下图中,已知,求、、的度数。
5.(23-24四年级上·湖南永州·期末)下图是一张长方形的纸,把它的一角折叠过来。已知∠1=50°求∠2。
6.(23-24四年级上·湖南永州·期末)已知∠3=35°,求∠4的度数。
7.(23-24四年级上·广东汕头·期末)如图,∠1=155°,求∠4的度数。
8.(23-24四年级上·河北保定·期末)下图是两个相同的长方形组成的图形,求∠1,∠2,∠3的度数。
21世纪教育网(www.21cnjy.com)
第三单元 《角的度量》 单元复习讲义(讲义)
四年级数学上册专项精练(知识梳理+典例精讲+专项精练)
线段、直线、射线的认识和特征
图形 端点的个数 延长情况 是否可测量
直线 0个 两端无限延长 无法测量
射线 1个 一端可以延长 无法测量
线段 2个 不可延长 可以测量
2、数线段的方法
(1)定义法:从基本线段数起;以某一点为左端点数起。
(2)公式法:
①加法公式:首先数出线段由几个端点,然后从1+2+3+……+(n-1),其中n代表端点数量。
②乘法公式:n×(n-1)÷2(其中n代表端点数量)。
1、角的定义:从一点引出两条射线所组成的图形叫做角。
2、角的各部分名称:这个公共端点叫做角的顶点,这两条射线叫做角的两条边。
3、角的表示方法:角通常用符号“∠”来表示,不同的角可以用数字区分,如∠1、∠2,但要在相应的图中表明。
1、角的计量单位:角的计量单位是“度”,用符号“°”表示。
将半圆(或圆)平均分成180(或360)等份,每一份所对的角的大小就是1度。
2、角的度量工具:量角器是度量角的工具。
3、角的度量方法
(1)把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合;
(2)角的另一边所对的量角器上的刻度,就是这个角的度数。
(3)与量角器0°刻度线重合的边向右,就看里圈的刻度数;相反就看外圈的刻度数。
角的名称 图形 意义 特征
锐角 小于的角叫作锐角。 < 锐角 <
直角 等于的角叫做直角。 直角 =
钝角 大于而小于的角叫作钝角。 < 钝角 <
平角 角的两边成一条直线,这时所形成的角是平角。 平角 =
周角 一条射线绕它的顶点旋转一周所形成的角是周角。 周角 =
1、锐角<直角<钝角<平角<周角;
2、1平角=2直角,1周角=2平角=4直角。
3、角的性质
角的大小与边的长短无关:角的大小只与两条边叉开的大小有关,叉开得越大,角越大。
放大镜不能放大角:放大镜可以改变物体的大小,但不能改变角的大小。
【典例精讲1】(四年级上·河南周口·期中)下图是一张长方形纸折起来以后的图形,如果∠2=70°
那么∠1=?
【答案】∠1=40°
【分析】如图,∠1+∠2+∠3=180°,由∠2=70°,得出180°-(∠2+∠3)=∠1,由对折可知∠3=∠2,进一步求得∠1即可。
【详解】∠1=180°-70°×2
=180°-140°
=40°
答:∠1是40°。
【点睛】此题考查利用对折重叠的两个角相等和平角等于180°来解决有关角度计算的问题。
【典例精讲2】(23-24四年级上·河北衡水·期末)如图,两张同样的长方形纸重叠了一部分,已知∠1=55°,分别求出∠2、∠3的度数。
【答案】∠2=35°,∠3=55°
【分析】根据图形,∠1+∠2=90°,因为∠1=55°,所以可以求出∠2的度数;又根据∠3+∠2=90°,继而可求出∠3度数,据此即可解答。
【详解】∠1+∠2=90°,∠1=55°,∠2=90°-55°=35°;
∠2+∠3=90°,所以∠3=90°-35°=55°
【典例精讲3】(22-23四年级上·江西宜春·期末)求出下面各角的度数。
已知如图中∠2=65°,求∠1。
【答案】50°
【分析】由图可知∠2+∠2+∠1=平角,平角为180°,所以∠1=180°-∠2-∠2;据此解答。
【详解】∠1=180°-65°-65°=50°
所以∠1为50°。
学校:___________ 姓名:___________ 班级:___________
计算题
1.(22-23四年级上·河南三门峡·期末)两个正方形叠放在一起,如图,求的度数。
【答案】15°
【分析】1直角=90°,1平角=180°,根据题意可知,∠1+∠3=90°,∠1+∠3+45°+∠2+30°=180°,由此可知,∠2=180°-30°-45°-(∠1+∠3),依此计算。
【详解】∠2=180°-30°-45°-90°
=150°-45°-90°
=105°-90°
=15°
∠2是15°。
2.(22-23四年级上·湖北孝感·期中)已知∠1=40°,∠5是直角,求∠2、∠3、∠4的度数。
【答案】∠2=50°;∠3=130°;∠4=50°
【分析】根据平角的定义,如果一个角的两条边互为反向延长线成为180°,这个角叫平角,平角的一半叫直角,利用图中角与角的关系即可求得。
【详解】因为∠1=40°,∠5是直角,
所以∠2=180°-90°-40°=50°;
∠3=180°-50°=130°;
∠4=180°-130°=50°;
∠2等于50°,∠3等于130°,∠4等于50°。
3.(23-24四年级上·湖南郴州·期中)如图,已知∠1=30°,求∠2的度数。
【答案】30°
【分析】假设∠1和∠2中间的角为∠3,观察发现∠1+∠3=90°,所以∠3=90°-∠1;∠3+∠2=90°,所以∠2=90°-∠3;据此解答。
【详解】∠3:90°-30°=60°
∠2:90°-60°=30°
∠2的度数为30°。
4.(22-23四年级上·黑龙江鸡西·期末)下图中,已知,求、、的度数。
【答案】∠2的度数是155°,∠3的度数是25°,∠4的度数是65°
【分析】根据对平角的认识,平角的度数为180度,要求∠2的度数,用180度减去∠1的度数,要求∠3的度数,用180度减去∠2即可,要求∠4的度数,用180度减去直角的度数,再减去∠3的度数,根据对直角的认识,直角的度数是90度,代入数据计算。
【详解】∠2=180°-∠1=180°-25°=155°
∠3=180°-∠2=180°-155°=25°
∠4=180°-90°-25°=90°-25°=65°
∠2的度数是155°,∠3的度数是25°,∠4的度数是65°。
5.(23-24四年级上·湖南永州·期末)下图是一张长方形的纸,把它的一角折叠过来。已知∠1=50°求∠2。
【答案】80°
【分析】由图可以看出是一张长方形纸折起来的图形,把这张纸展开后,以∠1、∠2的顶点为顶点的角是180°,由于∠1盖住了一个和它相等的角,展开后就是2∠1+∠2=180°,又知∠1=50°,据此可求出∠2的度数。
【详解】∠2=180°-2×∠1
=180°-2×50°
=180°-100°
=80°
即∠2=80°
6.(23-24四年级上·湖南永州·期末)已知∠3=35°,求∠4的度数。
【答案】∠4=55°
【分析】根据题图可知,∠3、∠4和一个直角组成一个平角,则∠3+∠4+90°=180°,∠4=180°-90°-∠3。
【详解】∠4=180°-90°-∠3=180°-90°-35°=55°。
即∠4=55°。
7.(23-24四年级上·广东汕头·期末)如图,∠1=155°,求∠4的度数。
【答案】115°
【分析】根据图形可知∠1+∠2=180°,∠1=155°,∠2=180°-155°;又因为∠3+∠2=90°,90°减去∠2即可得到∠3;最后因为∠3+∠4=180°,用180°减去∠3即可求出∠4。
【详解】∠2=180°-155°=25°
∠3=90°-25°=65°
∠4=180°-65°=115°
8.(23-24四年级上·河北保定·期末)下图是两个相同的长方形组成的图形,求∠1,∠2,∠3的度数。
【答案】∠1=64°
∠2=26°
∠3=110°
【分析】根据题图可知,∠1和26°的角组成一个直角,则∠1=90°-26°。∠1和∠2组成一个直角,则∠2=90°-∠1。∠3和70°的角组成一个平角,则∠3=180°-70°。
【详解】∠1=90°﹣26°=64°
∠2=90°﹣64°=26°
∠3=180°﹣70°=110°
21世纪教育网(www.21cnjy.com)
四年级数学上册专项精练(知识梳理+典例精讲+专项精练)
线段、直线、射线的认识和特征
图形 端点的个数 延长情况 是否可测量
直线 0个 两端无限延长 无法测量
射线 1个 一端可以延长 无法测量
线段 2个 不可延长 可以测量
2、数线段的方法
(1)定义法:从基本线段数起;以某一点为左端点数起。
(2)公式法:
①加法公式:首先数出线段由几个端点,然后从1+2+3+……+(n-1),其中n代表端点数量。
②乘法公式:n×(n-1)÷2(其中n代表端点数量)。
1、角的定义:从一点引出两条射线所组成的图形叫做角。
2、角的各部分名称:这个公共端点叫做角的顶点,这两条射线叫做角的两条边。
3、角的表示方法:角通常用符号“∠”来表示,不同的角可以用数字区分,如∠1、∠2,但要在相应的图中表明。
1、角的计量单位:角的计量单位是“度”,用符号“°”表示。
将半圆(或圆)平均分成180(或360)等份,每一份所对的角的大小就是1度。
2、角的度量工具:量角器是度量角的工具。
3、角的度量方法
(1)把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合;
(2)角的另一边所对的量角器上的刻度,就是这个角的度数。
(3)与量角器0°刻度线重合的边向右,就看里圈的刻度数;相反就看外圈的刻度数。
角的名称 图形 意义 特征
锐角 小于的角叫作锐角。 < 锐角 <
直角 等于的角叫做直角。 直角 =
钝角 大于而小于的角叫作钝角。 < 钝角 <
平角 角的两边成一条直线,这时所形成的角是平角。 平角 =
周角 一条射线绕它的顶点旋转一周所形成的角是周角。 周角 =
1、锐角<直角<钝角<平角<周角;
2、1平角=2直角,1周角=2平角=4直角。
3、角的性质
角的大小与边的长短无关:角的大小只与两条边叉开的大小有关,叉开得越大,角越大。
放大镜不能放大角:放大镜可以改变物体的大小,但不能改变角的大小。
【典例精讲1】(四年级上·河南周口·期中)下图是一张长方形纸折起来以后的图形,如果∠2=70°
那么∠1=?
【答案】∠1=40°
【分析】如图,∠1+∠2+∠3=180°,由∠2=70°,得出180°-(∠2+∠3)=∠1,由对折可知∠3=∠2,进一步求得∠1即可。
【详解】∠1=180°-70°×2
=180°-140°
=40°
答:∠1是40°。
【点睛】此题考查利用对折重叠的两个角相等和平角等于180°来解决有关角度计算的问题。
【典例精讲2】(23-24四年级上·河北衡水·期末)如图,两张同样的长方形纸重叠了一部分,已知∠1=55°,分别求出∠2、∠3的度数。
【答案】∠2=35°,∠3=55°
【分析】根据图形,∠1+∠2=90°,因为∠1=55°,所以可以求出∠2的度数;又根据∠3+∠2=90°,继而可求出∠3度数,据此即可解答。
【详解】∠1+∠2=90°,∠1=55°,∠2=90°-55°=35°;
∠2+∠3=90°,所以∠3=90°-35°=55°
【典例精讲3】(22-23四年级上·江西宜春·期末)求出下面各角的度数。
已知如图中∠2=65°,求∠1。
【答案】50°
【分析】由图可知∠2+∠2+∠1=平角,平角为180°,所以∠1=180°-∠2-∠2;据此解答。
【详解】∠1=180°-65°-65°=50°
所以∠1为50°。
学校:___________ 姓名:___________ 班级:___________
计算题
1.(22-23四年级上·河南三门峡·期末)两个正方形叠放在一起,如图,求的度数。
2.(22-23四年级上·湖北孝感·期中)已知∠1=40°,∠5是直角,求∠2、∠3、∠4的度数。
3.(23-24四年级上·湖南郴州·期中)如图,已知∠1=30°,求∠2的度数。
4.(22-23四年级上·黑龙江鸡西·期末)下图中,已知,求、、的度数。
5.(23-24四年级上·湖南永州·期末)下图是一张长方形的纸,把它的一角折叠过来。已知∠1=50°求∠2。
6.(23-24四年级上·湖南永州·期末)已知∠3=35°,求∠4的度数。
7.(23-24四年级上·广东汕头·期末)如图,∠1=155°,求∠4的度数。
8.(23-24四年级上·河北保定·期末)下图是两个相同的长方形组成的图形,求∠1,∠2,∠3的度数。
21世纪教育网(www.21cnjy.com)
第三单元 《角的度量》 单元复习讲义(讲义)
四年级数学上册专项精练(知识梳理+典例精讲+专项精练)
线段、直线、射线的认识和特征
图形 端点的个数 延长情况 是否可测量
直线 0个 两端无限延长 无法测量
射线 1个 一端可以延长 无法测量
线段 2个 不可延长 可以测量
2、数线段的方法
(1)定义法:从基本线段数起;以某一点为左端点数起。
(2)公式法:
①加法公式:首先数出线段由几个端点,然后从1+2+3+……+(n-1),其中n代表端点数量。
②乘法公式:n×(n-1)÷2(其中n代表端点数量)。
1、角的定义:从一点引出两条射线所组成的图形叫做角。
2、角的各部分名称:这个公共端点叫做角的顶点,这两条射线叫做角的两条边。
3、角的表示方法:角通常用符号“∠”来表示,不同的角可以用数字区分,如∠1、∠2,但要在相应的图中表明。
1、角的计量单位:角的计量单位是“度”,用符号“°”表示。
将半圆(或圆)平均分成180(或360)等份,每一份所对的角的大小就是1度。
2、角的度量工具:量角器是度量角的工具。
3、角的度量方法
(1)把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合;
(2)角的另一边所对的量角器上的刻度,就是这个角的度数。
(3)与量角器0°刻度线重合的边向右,就看里圈的刻度数;相反就看外圈的刻度数。
角的名称 图形 意义 特征
锐角 小于的角叫作锐角。 < 锐角 <
直角 等于的角叫做直角。 直角 =
钝角 大于而小于的角叫作钝角。 < 钝角 <
平角 角的两边成一条直线,这时所形成的角是平角。 平角 =
周角 一条射线绕它的顶点旋转一周所形成的角是周角。 周角 =
1、锐角<直角<钝角<平角<周角;
2、1平角=2直角,1周角=2平角=4直角。
3、角的性质
角的大小与边的长短无关:角的大小只与两条边叉开的大小有关,叉开得越大,角越大。
放大镜不能放大角:放大镜可以改变物体的大小,但不能改变角的大小。
【典例精讲1】(四年级上·河南周口·期中)下图是一张长方形纸折起来以后的图形,如果∠2=70°
那么∠1=?
【答案】∠1=40°
【分析】如图,∠1+∠2+∠3=180°,由∠2=70°,得出180°-(∠2+∠3)=∠1,由对折可知∠3=∠2,进一步求得∠1即可。
【详解】∠1=180°-70°×2
=180°-140°
=40°
答:∠1是40°。
【点睛】此题考查利用对折重叠的两个角相等和平角等于180°来解决有关角度计算的问题。
【典例精讲2】(23-24四年级上·河北衡水·期末)如图,两张同样的长方形纸重叠了一部分,已知∠1=55°,分别求出∠2、∠3的度数。
【答案】∠2=35°,∠3=55°
【分析】根据图形,∠1+∠2=90°,因为∠1=55°,所以可以求出∠2的度数;又根据∠3+∠2=90°,继而可求出∠3度数,据此即可解答。
【详解】∠1+∠2=90°,∠1=55°,∠2=90°-55°=35°;
∠2+∠3=90°,所以∠3=90°-35°=55°
【典例精讲3】(22-23四年级上·江西宜春·期末)求出下面各角的度数。
已知如图中∠2=65°,求∠1。
【答案】50°
【分析】由图可知∠2+∠2+∠1=平角,平角为180°,所以∠1=180°-∠2-∠2;据此解答。
【详解】∠1=180°-65°-65°=50°
所以∠1为50°。
学校:___________ 姓名:___________ 班级:___________
计算题
1.(22-23四年级上·河南三门峡·期末)两个正方形叠放在一起,如图,求的度数。
【答案】15°
【分析】1直角=90°,1平角=180°,根据题意可知,∠1+∠3=90°,∠1+∠3+45°+∠2+30°=180°,由此可知,∠2=180°-30°-45°-(∠1+∠3),依此计算。
【详解】∠2=180°-30°-45°-90°
=150°-45°-90°
=105°-90°
=15°
∠2是15°。
2.(22-23四年级上·湖北孝感·期中)已知∠1=40°,∠5是直角,求∠2、∠3、∠4的度数。
【答案】∠2=50°;∠3=130°;∠4=50°
【分析】根据平角的定义,如果一个角的两条边互为反向延长线成为180°,这个角叫平角,平角的一半叫直角,利用图中角与角的关系即可求得。
【详解】因为∠1=40°,∠5是直角,
所以∠2=180°-90°-40°=50°;
∠3=180°-50°=130°;
∠4=180°-130°=50°;
∠2等于50°,∠3等于130°,∠4等于50°。
3.(23-24四年级上·湖南郴州·期中)如图,已知∠1=30°,求∠2的度数。
【答案】30°
【分析】假设∠1和∠2中间的角为∠3,观察发现∠1+∠3=90°,所以∠3=90°-∠1;∠3+∠2=90°,所以∠2=90°-∠3;据此解答。
【详解】∠3:90°-30°=60°
∠2:90°-60°=30°
∠2的度数为30°。
4.(22-23四年级上·黑龙江鸡西·期末)下图中,已知,求、、的度数。
【答案】∠2的度数是155°,∠3的度数是25°,∠4的度数是65°
【分析】根据对平角的认识,平角的度数为180度,要求∠2的度数,用180度减去∠1的度数,要求∠3的度数,用180度减去∠2即可,要求∠4的度数,用180度减去直角的度数,再减去∠3的度数,根据对直角的认识,直角的度数是90度,代入数据计算。
【详解】∠2=180°-∠1=180°-25°=155°
∠3=180°-∠2=180°-155°=25°
∠4=180°-90°-25°=90°-25°=65°
∠2的度数是155°,∠3的度数是25°,∠4的度数是65°。
5.(23-24四年级上·湖南永州·期末)下图是一张长方形的纸,把它的一角折叠过来。已知∠1=50°求∠2。
【答案】80°
【分析】由图可以看出是一张长方形纸折起来的图形,把这张纸展开后,以∠1、∠2的顶点为顶点的角是180°,由于∠1盖住了一个和它相等的角,展开后就是2∠1+∠2=180°,又知∠1=50°,据此可求出∠2的度数。
【详解】∠2=180°-2×∠1
=180°-2×50°
=180°-100°
=80°
即∠2=80°
6.(23-24四年级上·湖南永州·期末)已知∠3=35°,求∠4的度数。
【答案】∠4=55°
【分析】根据题图可知,∠3、∠4和一个直角组成一个平角,则∠3+∠4+90°=180°,∠4=180°-90°-∠3。
【详解】∠4=180°-90°-∠3=180°-90°-35°=55°。
即∠4=55°。
7.(23-24四年级上·广东汕头·期末)如图,∠1=155°,求∠4的度数。
【答案】115°
【分析】根据图形可知∠1+∠2=180°,∠1=155°,∠2=180°-155°;又因为∠3+∠2=90°,90°减去∠2即可得到∠3;最后因为∠3+∠4=180°,用180°减去∠3即可求出∠4。
【详解】∠2=180°-155°=25°
∠3=90°-25°=65°
∠4=180°-65°=115°
8.(23-24四年级上·河北保定·期末)下图是两个相同的长方形组成的图形,求∠1,∠2,∠3的度数。
【答案】∠1=64°
∠2=26°
∠3=110°
【分析】根据题图可知,∠1和26°的角组成一个直角,则∠1=90°-26°。∠1和∠2组成一个直角,则∠2=90°-∠1。∠3和70°的角组成一个平角,则∠3=180°-70°。
【详解】∠1=90°﹣26°=64°
∠2=90°﹣64°=26°
∠3=180°﹣70°=110°
21世纪教育网(www.21cnjy.com)
