5.1圆的认识(讲义)(知识梳理 专项练习)六年级数学上册人教版
文档属性
| 名称 | 5.1圆的认识(讲义)(知识梳理 专项练习)六年级数学上册人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 323.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-18 08:40:42 | ||
图片预览



文档简介
5.1圆的认识(讲义)
(知识梳理+专项练习)
1、圆的定义:圆是由曲线围成的一种平面图形。
2、圆心:将一张圆形纸片对折两次,折痕相交于圆中心的一点,这一点叫做圆心。一般用字母O表示。它到圆上任意一点的距离都相等.
3、半径:连接圆心到圆上任意一点的线段叫做半径。一般用字母r表示。把圆规两脚分开,两脚之间的距离就是圆的半径。
4、直径:通过圆心并且两端都在圆上的线段叫做直径。一般用字母d表示。直径是一个圆内最长的线段。
5、圆心确定圆的位置,半径确定圆的大小。
6、在同一个圆内或等圆内,有无数条半径,有无数条直径。所有的半径都相等,所有的直径都相等。
7.在同圆或等圆内,直径的长度是半径的2倍,半径的长度是直径的。
用字母表示为:d=2r或r=d÷2
8、轴对称图形:如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形是轴对称图形。折痕所在的这条直线叫做对称轴。
9、长方形、正方形和圆都是对称图形,都有对称轴。这些图形都是轴对称图形。
10、只有1条对称轴的图形有: 角、等腰三角形、等腰梯形、扇形、半圆;只有2条对称轴的图形是: 长方形;只有3条对称轴的图形是: 等边三角形;只有4条对称轴的图形是: 正方形;有无数条对称轴的图形是: 圆、圆环。
11、画对称轴要用铅笔画,同时要用尺子(三角板)画出虚线,这条虚线两端要超出图形一点。
一、选择题
1.以下对称轴条数最多的是( )。
A.正方形 B.长方形 C.圆 D.半圆
2.A,B,C,D四个小朋友玩套圈游戏(点O为所要套的物品),下面的站法中公平的有( )。
A. B. C. D.
3.下列说法错误的是( )。
A.圆是曲线图形 B.圆具有对称性 C.半径一定比直径短
4.从圆心到圆上任意一点的线段叫做( )
A.直径 B.半径 C.直线
二、填空题
5.在同一个圆里,所有的半径都( ),所有的( )也都相等,半径等于直径的.
6.求半径或直径。
7.在一个周长为20cm的正方形纸片内,要剪一个最大的圆,这个圆的半径是( )cm。
三、判断题
8.两段都在圆上并且经过圆心的线段是直径。 ( )
9.在一个长8厘米,宽6厘米的长方形纸中剪下一个最大的圆,这个圆的直径是8厘米。( )
10.画直径是10cm的圆,圆规两脚之间的距离是10cm。( )
11.正方形、长方形、半圆和等边三角形中,对称轴条数最多的是正方形。( )
四、解答题
12.下图是三个相同的圆组成的平面图形,依次连接三个圆的圆心的线段所围成的三角形中,每一个角的度数分别是多少?
13.画出以点O为圆心,半径为3厘米的圆。找到并描出点A(2,4),点A与点B连接后,AB正好是圆的直径,点B( )。
14.想一想,我们已经学过的平面图形中哪些是轴对称图形?哪些图形的对称轴只有一条?哪些不止一条?
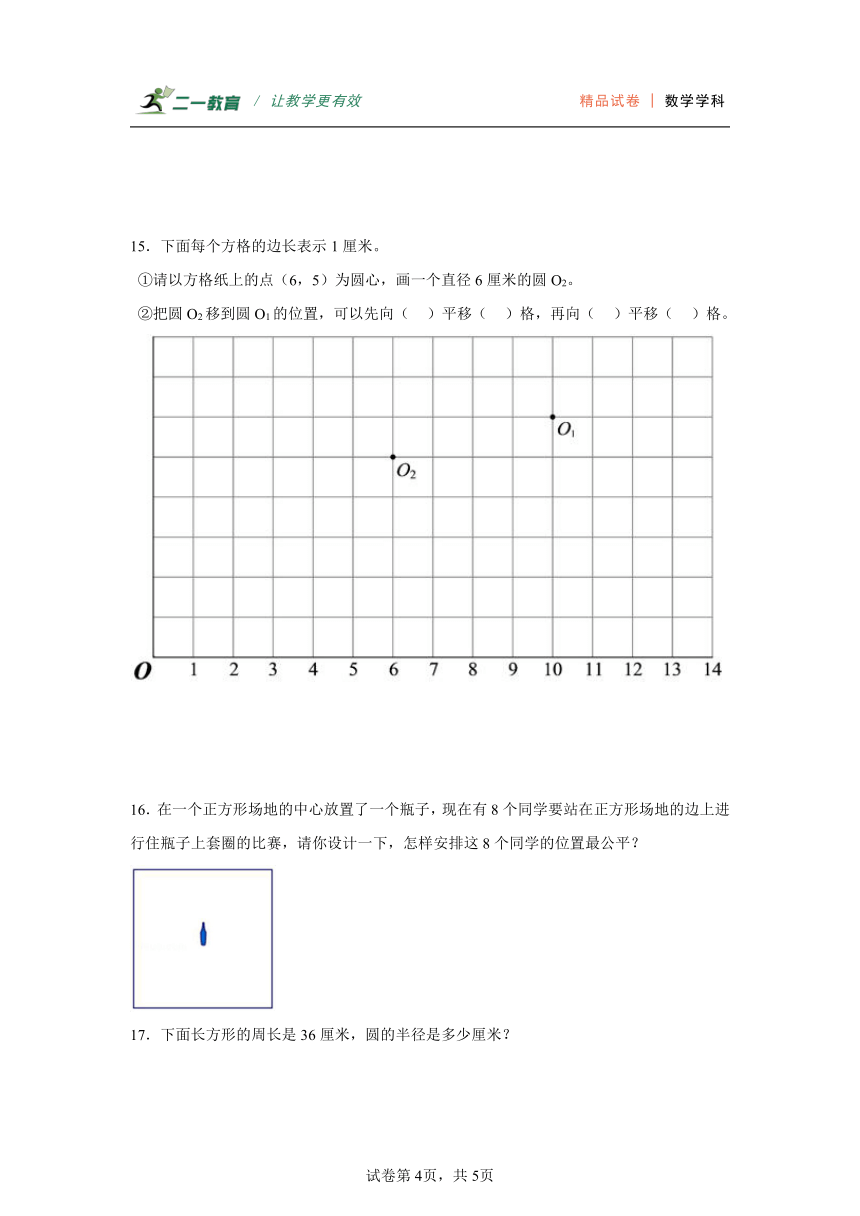
15.下面每个方格的边长表示1厘米。
①请以方格纸上的点(6,5)为圆心,画一个直径6厘米的圆O2。
②把圆O2移到圆O1的位置,可以先向( )平移( )格,再向( )平移( )格。
16.在一个正方形场地的中心放置了一个瓶子,现在有8个同学要站在正方形场地的边上进行住瓶子上套圈的比赛,请你设计一下,怎样安排这8个同学的位置最公平?
17.下面长方形的周长是36厘米,圆的半径是多少厘米?
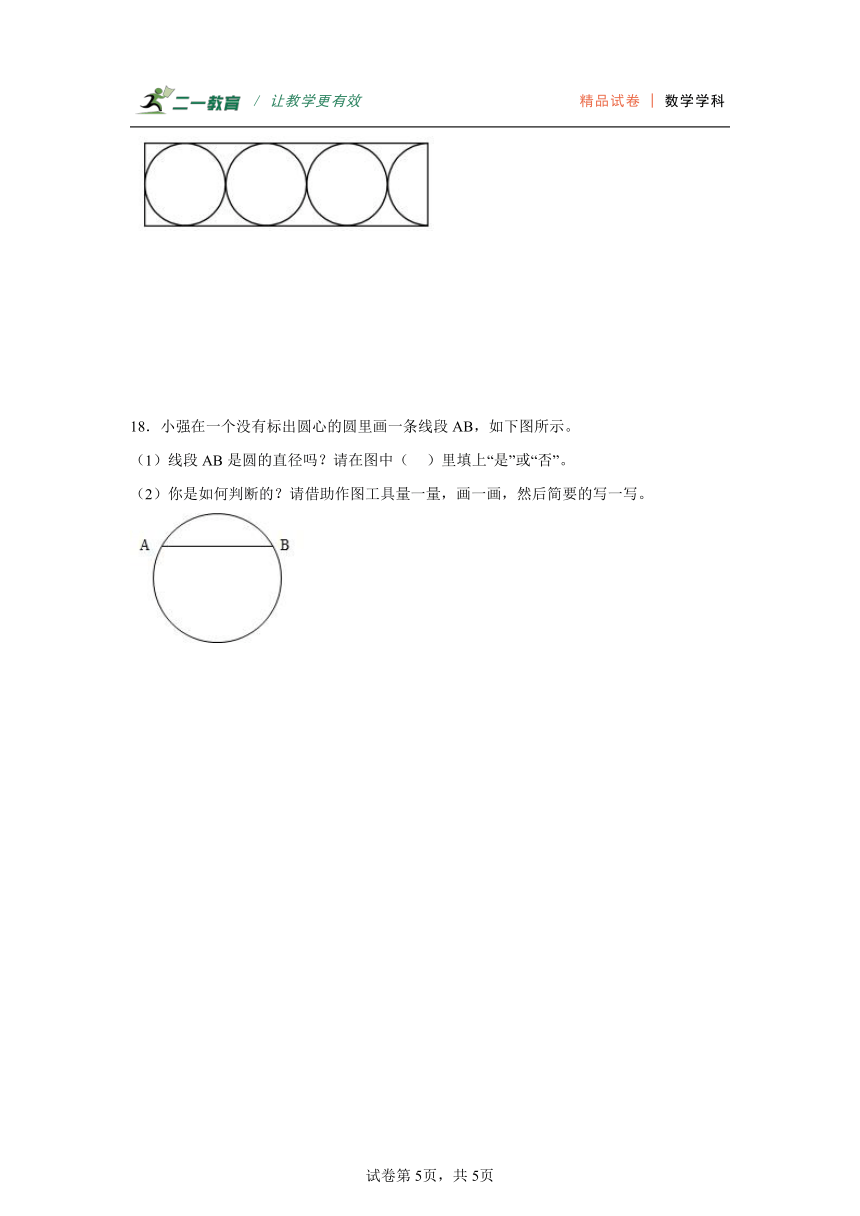
18.小强在一个没有标出圆心的圆里画一条线段AB,如下图所示。
(1)线段AB是圆的直径吗?请在图中( )里填上“是”或“否”。
(2)你是如何判断的?请借助作图工具量一量,画一画,然后简要的写一写。
/ 让教学更有效 精品试卷 | 数学学科
/ 让教学更有效 精品试卷 | 数学学科
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形就叫轴对称图形;根据轴对称图形的定义,先找出各个图形的对称轴的条数,再进行对比选择即可。
【详解】A.正方形有4条对称轴;
B.长方形有2条对称轴;
C.圆有无数条对称轴;
D.半圆有1条对称轴;
故对称轴最多的是圆;
故答案为:C。
【点睛】此题主要考查了轴对称图形的定义,能够正确说出轴对称图形的对称轴是解题关键。
2.AD
【分析】想要站法公平,需要每一位小朋友到O点的距离相等,验证各选项中每位小朋友距离O点的距离是否相等。
【详解】
A. 正方形四个顶点到对角线交点的距离相等,站法公平;
B. ,连接AO、BO, AO>BO,站法不公平;
C. ,连接AO、CO,CO>AO,站法不公平;
D. ,每一个同学到O点的距离都是圆的半径,在同一个圆中,所有的半径都相等,站法公平。
故答案为:AD
3.C
【分析】如图,圆是一种几何图形,当一条线段绕着它的一个端点在平面内旋转一周时,它的另一个端点的轨迹叫做圆。
【详解】A.圆是曲线图形,说法正确;
B.圆具有对称性,且有无数条对称轴,选项说法正确;
C.同一个圆内,半径一定比直径短,选项说法错误。
故答案为:C
【点睛】关键是熟悉圆的特征,注意同圆和等圆的直径=半径×2。
4.B
【详解】根据半径的含义可知:从圆心到圆上任意一点的线段叫做半径.
故选B.
5.相等;直径;
【解析】略
6.7;;
;3.6;
【分析】根据直径=半径×2,半径=直径÷2,计算即可。
【详解】3.5×2=7(分米);÷2=(分米);×2=(厘米)
×2=(米);7.2÷2=3.6(厘米);÷2=(米)
【点睛】关键是理解同一圆内,直径和半径之间的关系。
7.2.5
【分析】在正方形内剪一个最大的圆,圆的直径和正方形的边长相等,用正方形的周长除以4即可求出边长,即圆的直径,再进一步求出半径即可。
【详解】20÷4÷2
=5÷2
=2.5(cm)
所以,在一个周长为20cm的正方形纸片内,要剪一个最大的圆,这个圆的半径是2.5cm。
【点睛】解答本题的关键是要明确在正方形内剪一个最大的圆,圆的直径与正方形边长的关系。
8.√
【详解】略
9.×
【分析】长方形中剪下一个最大的圆,圆的直径=长方形的宽,据此分析。
【详解】在一个长8厘米,宽6厘米的长方形纸中剪下一个最大的圆,这个圆的直径是6厘米,所以原题说法错误。
故答案为:×
【点睛】关键是熟悉圆的特征,理解长方形和圆之间的关系。
10.×
【分析】根据题意,画直径是10cm的圆,那么圆的半径是(10÷2)cm,圆规两脚之间的距离等于所画圆的半径;据此判断。
【详解】用圆规画一个直径是10cm的圆,圆规两脚之间的距离应是:
10÷2=5(cm)
原题说法错误。
故答案为:×
【点睛】明确圆规两脚之间的距离等于所画圆的半径,利用直径与半径的关系解答。
11.√
【分析】先判断出正方形、长方形、半圆和等边三角形的对称轴数量,再判断出对称轴中数量最多的图形即可。
【详解】正方形有4条对称轴,长方形有2条对称轴,半圆有1条对称轴,等边三角形有3条对称轴。所以,这四个图形中,对称轴数量最多的是正方形。
故答案为:√
【点睛】本题考查了对称轴,明确常见图形有几条对称轴是解题的关键。
12.60°;60°;60°
【详解】因为三个圆相等,所以三个圆的半径都相等,所以三角形的每条边的长都是2r,所以三角形的三条边相等。
因此,围成的三角形是等边三角形,等边三角形的每一个内角都等于60°
13.见详解;(8,4)
【分析】根据数对的表示方法:(列数,行数),第一个数字表示列,第二个数字表示行,据此找到圆心在方格中的位置,然后画一个半径是3厘米的圆即可。根据数对找出点A在方格中的对应位置,连接点A和点O,向右延长直至与圆相交,相交点即是点B所在的位置,用数对表示出来即可。
【详解】如图:
点B用数对表示是(8,4)。
【点睛】此题主要考查用数对表示位置、根据数对找位置以及画圆的方法。
14.见详解
【分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴。据此根据学过的平面图形的特征,进行分析。
【详解】
我们学过的平面图形中是轴对称图形的有:长方形、正方形、等腰三角形、等腰梯形、圆。
对称轴只有一条的有:等腰三角形、等腰梯形。
对称轴不止一条的有:长方形、正方形、圆。
【点睛】关键是掌握轴对称图形的特点,熟悉各种图形的特征。
15.①
②右;4;上;1(或上;1;右;4)
【详解】略
【点睛】本题是确定位置以及圆相关知识的综合应用题,让学生在动手的同时又动脑。主要目的是考查学生对用数对确定位置、用圆规画圆等的掌握程度以及综合应用知识的能力。
16.以被套物体为圆心,8个同学站成一个圆,游戏规则才公平
【详解】略
17.2厘米
【分析】观察图形可知,长方形的长等于圆的半径的7倍,长方形的宽等于圆的半径的2倍,设圆的半径为x厘米,长方形的长为7x厘米,宽为2x厘米;根据长方形周长公式:周长=(长+宽)×2,长+宽=周长÷2,据此列方程:7x+2x=36÷2,解方程,即可解答。
【详解】解:设圆的半径为x厘米,则长方形的长是7x厘米,宽为2x厘米。
7x+2x=36÷2
9x=18
x=18÷9
x=2
答:圆的半径是2厘米。
18.(1)否;
(2)借助直尺测量找出圆的直径,AB不是圆中最长的线段。
【分析】圆的直径是圆中最长的线段,线段AB显然不是圆中最长的线段,故AB不是圆的直径;可利用直尺进行测量,进而得出答案。
【详解】(1)圆的直径是圆中最长的线段,线段AB显然不是圆中最长的线段,故AB不是圆的直径;
(2)测量方法:
如图,将尺子一段固定于圆上任意一点,移动尺子的另一端,测量出圆内“最长的线段”,就是该圆的直径。
【点睛】本题主要考查的是圆的直径,解题的关键是牢记并合理利用圆的直径相关知识,进而得出答案。
答案第1页,共2页
答案第1页,共2页
(知识梳理+专项练习)
1、圆的定义:圆是由曲线围成的一种平面图形。
2、圆心:将一张圆形纸片对折两次,折痕相交于圆中心的一点,这一点叫做圆心。一般用字母O表示。它到圆上任意一点的距离都相等.
3、半径:连接圆心到圆上任意一点的线段叫做半径。一般用字母r表示。把圆规两脚分开,两脚之间的距离就是圆的半径。
4、直径:通过圆心并且两端都在圆上的线段叫做直径。一般用字母d表示。直径是一个圆内最长的线段。
5、圆心确定圆的位置,半径确定圆的大小。
6、在同一个圆内或等圆内,有无数条半径,有无数条直径。所有的半径都相等,所有的直径都相等。
7.在同圆或等圆内,直径的长度是半径的2倍,半径的长度是直径的。
用字母表示为:d=2r或r=d÷2
8、轴对称图形:如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形是轴对称图形。折痕所在的这条直线叫做对称轴。
9、长方形、正方形和圆都是对称图形,都有对称轴。这些图形都是轴对称图形。
10、只有1条对称轴的图形有: 角、等腰三角形、等腰梯形、扇形、半圆;只有2条对称轴的图形是: 长方形;只有3条对称轴的图形是: 等边三角形;只有4条对称轴的图形是: 正方形;有无数条对称轴的图形是: 圆、圆环。
11、画对称轴要用铅笔画,同时要用尺子(三角板)画出虚线,这条虚线两端要超出图形一点。
一、选择题
1.以下对称轴条数最多的是( )。
A.正方形 B.长方形 C.圆 D.半圆
2.A,B,C,D四个小朋友玩套圈游戏(点O为所要套的物品),下面的站法中公平的有( )。
A. B. C. D.
3.下列说法错误的是( )。
A.圆是曲线图形 B.圆具有对称性 C.半径一定比直径短
4.从圆心到圆上任意一点的线段叫做( )
A.直径 B.半径 C.直线
二、填空题
5.在同一个圆里,所有的半径都( ),所有的( )也都相等,半径等于直径的.
6.求半径或直径。
7.在一个周长为20cm的正方形纸片内,要剪一个最大的圆,这个圆的半径是( )cm。
三、判断题
8.两段都在圆上并且经过圆心的线段是直径。 ( )
9.在一个长8厘米,宽6厘米的长方形纸中剪下一个最大的圆,这个圆的直径是8厘米。( )
10.画直径是10cm的圆,圆规两脚之间的距离是10cm。( )
11.正方形、长方形、半圆和等边三角形中,对称轴条数最多的是正方形。( )
四、解答题
12.下图是三个相同的圆组成的平面图形,依次连接三个圆的圆心的线段所围成的三角形中,每一个角的度数分别是多少?
13.画出以点O为圆心,半径为3厘米的圆。找到并描出点A(2,4),点A与点B连接后,AB正好是圆的直径,点B( )。
14.想一想,我们已经学过的平面图形中哪些是轴对称图形?哪些图形的对称轴只有一条?哪些不止一条?
15.下面每个方格的边长表示1厘米。
①请以方格纸上的点(6,5)为圆心,画一个直径6厘米的圆O2。
②把圆O2移到圆O1的位置,可以先向( )平移( )格,再向( )平移( )格。
16.在一个正方形场地的中心放置了一个瓶子,现在有8个同学要站在正方形场地的边上进行住瓶子上套圈的比赛,请你设计一下,怎样安排这8个同学的位置最公平?
17.下面长方形的周长是36厘米,圆的半径是多少厘米?
18.小强在一个没有标出圆心的圆里画一条线段AB,如下图所示。
(1)线段AB是圆的直径吗?请在图中( )里填上“是”或“否”。
(2)你是如何判断的?请借助作图工具量一量,画一画,然后简要的写一写。
/ 让教学更有效 精品试卷 | 数学学科
/ 让教学更有效 精品试卷 | 数学学科
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形就叫轴对称图形;根据轴对称图形的定义,先找出各个图形的对称轴的条数,再进行对比选择即可。
【详解】A.正方形有4条对称轴;
B.长方形有2条对称轴;
C.圆有无数条对称轴;
D.半圆有1条对称轴;
故对称轴最多的是圆;
故答案为:C。
【点睛】此题主要考查了轴对称图形的定义,能够正确说出轴对称图形的对称轴是解题关键。
2.AD
【分析】想要站法公平,需要每一位小朋友到O点的距离相等,验证各选项中每位小朋友距离O点的距离是否相等。
【详解】
A. 正方形四个顶点到对角线交点的距离相等,站法公平;
B. ,连接AO、BO, AO>BO,站法不公平;
C. ,连接AO、CO,CO>AO,站法不公平;
D. ,每一个同学到O点的距离都是圆的半径,在同一个圆中,所有的半径都相等,站法公平。
故答案为:AD
3.C
【分析】如图,圆是一种几何图形,当一条线段绕着它的一个端点在平面内旋转一周时,它的另一个端点的轨迹叫做圆。
【详解】A.圆是曲线图形,说法正确;
B.圆具有对称性,且有无数条对称轴,选项说法正确;
C.同一个圆内,半径一定比直径短,选项说法错误。
故答案为:C
【点睛】关键是熟悉圆的特征,注意同圆和等圆的直径=半径×2。
4.B
【详解】根据半径的含义可知:从圆心到圆上任意一点的线段叫做半径.
故选B.
5.相等;直径;
【解析】略
6.7;;
;3.6;
【分析】根据直径=半径×2,半径=直径÷2,计算即可。
【详解】3.5×2=7(分米);÷2=(分米);×2=(厘米)
×2=(米);7.2÷2=3.6(厘米);÷2=(米)
【点睛】关键是理解同一圆内,直径和半径之间的关系。
7.2.5
【分析】在正方形内剪一个最大的圆,圆的直径和正方形的边长相等,用正方形的周长除以4即可求出边长,即圆的直径,再进一步求出半径即可。
【详解】20÷4÷2
=5÷2
=2.5(cm)
所以,在一个周长为20cm的正方形纸片内,要剪一个最大的圆,这个圆的半径是2.5cm。
【点睛】解答本题的关键是要明确在正方形内剪一个最大的圆,圆的直径与正方形边长的关系。
8.√
【详解】略
9.×
【分析】长方形中剪下一个最大的圆,圆的直径=长方形的宽,据此分析。
【详解】在一个长8厘米,宽6厘米的长方形纸中剪下一个最大的圆,这个圆的直径是6厘米,所以原题说法错误。
故答案为:×
【点睛】关键是熟悉圆的特征,理解长方形和圆之间的关系。
10.×
【分析】根据题意,画直径是10cm的圆,那么圆的半径是(10÷2)cm,圆规两脚之间的距离等于所画圆的半径;据此判断。
【详解】用圆规画一个直径是10cm的圆,圆规两脚之间的距离应是:
10÷2=5(cm)
原题说法错误。
故答案为:×
【点睛】明确圆规两脚之间的距离等于所画圆的半径,利用直径与半径的关系解答。
11.√
【分析】先判断出正方形、长方形、半圆和等边三角形的对称轴数量,再判断出对称轴中数量最多的图形即可。
【详解】正方形有4条对称轴,长方形有2条对称轴,半圆有1条对称轴,等边三角形有3条对称轴。所以,这四个图形中,对称轴数量最多的是正方形。
故答案为:√
【点睛】本题考查了对称轴,明确常见图形有几条对称轴是解题的关键。
12.60°;60°;60°
【详解】因为三个圆相等,所以三个圆的半径都相等,所以三角形的每条边的长都是2r,所以三角形的三条边相等。
因此,围成的三角形是等边三角形,等边三角形的每一个内角都等于60°
13.见详解;(8,4)
【分析】根据数对的表示方法:(列数,行数),第一个数字表示列,第二个数字表示行,据此找到圆心在方格中的位置,然后画一个半径是3厘米的圆即可。根据数对找出点A在方格中的对应位置,连接点A和点O,向右延长直至与圆相交,相交点即是点B所在的位置,用数对表示出来即可。
【详解】如图:
点B用数对表示是(8,4)。
【点睛】此题主要考查用数对表示位置、根据数对找位置以及画圆的方法。
14.见详解
【分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴。据此根据学过的平面图形的特征,进行分析。
【详解】
我们学过的平面图形中是轴对称图形的有:长方形、正方形、等腰三角形、等腰梯形、圆。
对称轴只有一条的有:等腰三角形、等腰梯形。
对称轴不止一条的有:长方形、正方形、圆。
【点睛】关键是掌握轴对称图形的特点,熟悉各种图形的特征。
15.①
②右;4;上;1(或上;1;右;4)
【详解】略
【点睛】本题是确定位置以及圆相关知识的综合应用题,让学生在动手的同时又动脑。主要目的是考查学生对用数对确定位置、用圆规画圆等的掌握程度以及综合应用知识的能力。
16.以被套物体为圆心,8个同学站成一个圆,游戏规则才公平
【详解】略
17.2厘米
【分析】观察图形可知,长方形的长等于圆的半径的7倍,长方形的宽等于圆的半径的2倍,设圆的半径为x厘米,长方形的长为7x厘米,宽为2x厘米;根据长方形周长公式:周长=(长+宽)×2,长+宽=周长÷2,据此列方程:7x+2x=36÷2,解方程,即可解答。
【详解】解:设圆的半径为x厘米,则长方形的长是7x厘米,宽为2x厘米。
7x+2x=36÷2
9x=18
x=18÷9
x=2
答:圆的半径是2厘米。
18.(1)否;
(2)借助直尺测量找出圆的直径,AB不是圆中最长的线段。
【分析】圆的直径是圆中最长的线段,线段AB显然不是圆中最长的线段,故AB不是圆的直径;可利用直尺进行测量,进而得出答案。
【详解】(1)圆的直径是圆中最长的线段,线段AB显然不是圆中最长的线段,故AB不是圆的直径;
(2)测量方法:
如图,将尺子一段固定于圆上任意一点,移动尺子的另一端,测量出圆内“最长的线段”,就是该圆的直径。
【点睛】本题主要考查的是圆的直径,解题的关键是牢记并合理利用圆的直径相关知识,进而得出答案。
答案第1页,共2页
答案第1页,共2页
