第2单元多边形的面积重难点应用题专项突破-数学五年级上册苏教版(含解析)
文档属性
| 名称 | 第2单元多边形的面积重难点应用题专项突破-数学五年级上册苏教版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 565.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-18 08:45:12 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第2单元多边形的面积重难点应用题专项突破-数学五年级上册苏教版
一、解答题
1.如图所示,李大爷靠墙围了一块菜地,围菜地的篱笆长36m,求这块菜地的面积。
2.某实验小学有一块劳动实践基地(如图)。这块地的面积是多少平方米?
3.有一块平行四边形的苗圃,底是80米,高是40米。如果每平方米种4棵腊梅苗,这个苗圃共种腊梅苗多少棵?
4.一个平行四边形的停车场,底是44米,高是64米,平均每辆车子占地16平方米。
5.“愉快劳动,成果共享”,实验小学利用学校闲置的空地,建起一块“种植园”作为劳动实践基地,形状如下图,这块劳动实践基地的面积是多少平方米?
6.如图,学校要在一块平行四边形的草地中间建造一个梯形的休息区,草地的面积还剩多少?
7.用48米长的篱笆,在靠墙的地方围一块菜地(如图)。这块菜地的面积是多少平方米?如果按照每平方米菜地一年能收入16.5元计算,这块菜地一年能收入多少元?
8.一块三角形玉米地,底是20米,高是15米,共收玉米300千克,平均每平方米收玉米多少千克?
9.植物是制造氧气的“工厂”,根据测算,1平方米的草坪每天能够释放约800克的氧气。
(1)如图,在一块梯形草坪中间有一条宽1米的石子路。这块草坪面积是多少平方米?
(2)这块草坪一个月(30天)大约能释放氧气多少千克?
10.建党100周年之际,某革命教育展览馆计划把原来的等腰梯形展区扩建成一个长方形展区(如图),求展区面积比原来增加了多少平方米?
11.实验小学五年级一班的学生要为学校运动会准备60面红旗,红旗形状为同样大小的直角三角形,每面红旗的两条直角边长分别是32厘米和24厘米。学校为他们准备了一块面积是2平方米的红布,够不够用?如果不够用,至少还需要多少平方厘米红布?
12.一个梯形如果上底增加4厘米,下底和高都不变,它的面积增加12平方厘米;如果高增加4厘米,上、下底都不变,面积增加16平方厘米。原梯形的面积是多少平方厘米?
13.一个三角形硬纸板的面积是440平方厘米,它的底是40厘米,高是多少厘米?
14.一个底是70米,高是25米平行四边形菜地,它的面积是多少平方米?
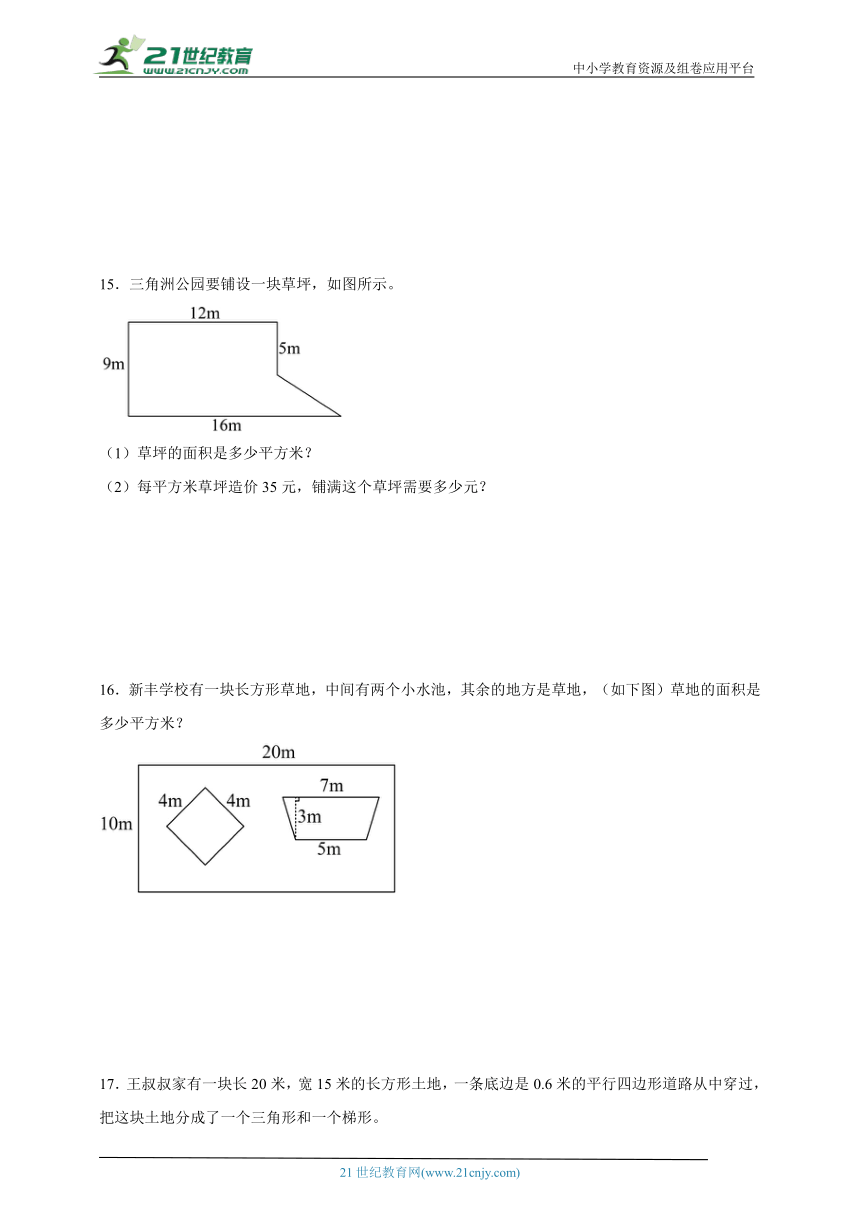
15.三角洲公园要铺设一块草坪,如图所示。
(1)草坪的面积是多少平方米?
(2)每平方米草坪造价35元,铺满这个草坪需要多少元?
16.新丰学校有一块长方形草地,中间有两个小水池,其余的地方是草地,(如下图)草地的面积是多少平方米?
17.王叔叔家有一块长20米,宽15米的长方形土地,一条底边是0.6米的平行四边形道路从中穿过,把这块土地分成了一个三角形和一个梯形。
(1)请你在图中画出这条小路的位置和形状。
(2)这条小路的面积是多少平方米?
18.小兰在一组平行线之间画了三个图形(如下图),观察三个图形,你觉得哪个图形的面积最大?请说明理由。
参考答案:
1.144平方米
【分析】由图片可知,菜地是一个梯形,上底+下底+高=36米,高=12米,则上底+下底=36-12=24米,梯形面积=(上底+下底)×高÷2,打入数据计算解答。
【详解】(36-12)×12÷2
=24×12÷2
=288÷2
=144(平方米)
答:这块菜地面积是144平方米。
2.64平方米
【分析】如图,将整个实践基地分为两个部分。其中①是一个上底为2米、下底为8米,高为8米的直角梯形;②是一个底为6米、高为8米的直角三角形。可以分别计算出两部分的面积再相加。
【详解】梯形面积:(2+8)×8÷2
=10×8÷2
=80÷2
=40(平方米)
三角形面积:6×8÷2
=48÷2
=24(平方米)
共:40+24=64(平方米)
答:这块地的面积是64平方米。
3.12800棵
【分析】先根据平行四边形的面积=底×高,用80×40求出这个苗圃的面积是3200平方米;每平方米种4棵腊梅苗,求这个苗圃共种的腊梅的棵数,也就是求3200个4是多少,用乘法计算,列式为4×3200。
【详解】4×(80×40)
=4×3200
=12800(棵)
答:这个苗圃共种腊梅苗12800棵。
4.够
【分析】利用平行四边形的面积公式先求出这个停车场的总面积,根据已知平均每辆车子占地16平方米,利用除法即可求得最多可以停放的车辆数。
【详解】44×64÷16
=2816÷16
=176(辆)
176>150可以停放150辆车。
答:这个停车场可以停放150辆车。
5.1330平方米
【分析】观察图形可知,实践基地的面积相当于一个三角形的面积加上一个平行四边形的面积,根据三角形的面积=底×高÷2,用35×12÷2即可求出三角形的面积;再根据平行四边形的面积=底×高,用28×40即可求出平行四边形的面积,然后将两部分相加即可。
【详解】35×12÷2=210(平方米)
28×40=1120(平方米)
210+1120=1330(平方米)
答:这块劳动实践基地的面积是1330平方米。
6.160平方米
【分析】观察图形可知,用平行四边形草地的面积减去梯形休息区的面积即可求出草地剩下的面积。平行四边形的面积=底×高,梯形的面积=(上底+下底)×高÷2,据此解答。
【详解】18×10-(3+7)×4÷2
=180-10×4÷2
=180-20
=160(平方米)
答:草地的面积还剩160平方米。
7.4752元
【分析】根据对图的观察,该菜地为一个直角梯形,48米篱笆的长度为该梯形的上底、下底和高的和,高为24米,用48减24,可求出该梯形菜地的上底与下底的和,根据梯形面积公式:S=(上底+下底)×高÷2,代入数据求出该菜地的面积,最后乘16.5,即可求出这个菜地一年的收入有多少元。
【详解】由分析可知:
(48-24)×24÷2
=24×24÷2
=576÷2
=288(平方米)
288×16.5=4752(元)
答:这块菜地的面积是288平方米,这块菜地一年能收入4752元。
【点睛】本题考查了梯形面积公式的应用,熟记公式是解题的关键。
8.2千克
【分析】根据三角形的面积公式:S=ah÷2,据此求出玉米地的面积;再根据除法的意义,用收玉米的重量除以玉米地的面积即可求出平均每平方米收玉米多少千克。
【详解】20×15÷2
=300÷2
=150(平方米)
300÷150=2(千克)
答:平均每平方米收玉米2千克。
9.(1)1470平方米
(2)35280千克
【分析】(1)观察图形可知,草坪的面积=梯形的面积-平行四边形的面积;根据梯形的面积=(上底+下底)×高÷2,平行四边形的面积=底×高,代入数据计算求解。
(2)已知1平方米的草坪每天能够释放约800克的氧气,根据进率“1千克=1000克”,把800克换算成0.8千克;
用1平方米的草坪每天释放氧气的质量乘草坪的面积,求出这块草坪每天释放氧气的质量,再乘30,即是这块草坪一个月(30天)大约能释放氧气的质量。
【详解】(1)梯形的面积:
(36+50)×35÷2
=86×35÷2
=3010÷2
=1505(平方米)
平行四边形的面积:1×35=35(平方米)
草坪的面积:1505-35=1470(平方米)
答:这块草坪面积是1470平方米。
(2)800克=0.8千克
0.8×1470×30
=1176×30
=35280(千克)
答:这块草坪一个月(30天)大约能释放氧气35280千克。
10.425平方米
【分析】先根据长方形的面积=长×宽,用62×25求出长方形的面积;再根据梯形的面积=(上底+下底)×高÷2,用(28+62)×25÷2求出梯形的面积;最后用长方形的面积减去梯形的面积,即可求出展区面积比原来增加了多少平方米。
【详解】62×25-(28+62)×25÷2
=1550-90×25÷2
=1550-2250÷2
=1550-1125
=425(平方米)
答:展区面积比原来增加了425平方米。
11.3040平方厘米
【分析】先根据三角形的面积=底×高÷2,代入数据求出每面红旗的面积;再乘60,求出做60块红旗需要的红布的总面积;然后根据1平方米=10000平方厘米,高级单位转化为低级单位乘进率,将2平方米换算成20000平方厘米,与做60块红旗需要的红布的总面积比较大下后求差即可。
【详解】32×24÷2×60
=768÷2×60
=384×60
=23040(平方厘米)
2平方米=20000平方厘米
23040>20000
23040-20000=3040(平方厘米)
答:至少还需要3040平方厘米红布。
【点睛】解答本题需熟练掌握三角形的面积公式,明确面积单位之间的进率。
12.24平方厘米
【分析】已知一个梯形的下底和高都不变,如果上底增加4厘米,面积增加12平方厘米,增加的是一个底为4厘米,高等于原梯形的高的三角形;根据三角形的高=三角形的面积×2÷底,即可求出三角形的高,也就是原梯形的高;
已知这个梯形的上、下底都不变,如果高增加4厘米,面积增加16平方厘米;根据梯形的上、下底之和=梯形的面积×2÷高,由此求出原梯形的上、下底之和;
最后根据梯形的面积=(上底+下底)×高÷2,代入数据计算,即可求出原梯形的面积。
【详解】原梯形的高:
12×2÷4
=24÷4
=6(厘米)
原梯形上、下底之和:
16×2÷4
=32÷4
=8(厘米)
原梯形的面积:
8×6÷2
=48÷2
=24(平方厘米)
答:原梯形的面积是24平方厘米。
【点睛】本题考查梯形面积、三角形面积公式的灵活运用,求出原梯形的高与上、下底之和是解题的关键。
13.22厘米
【分析】根据三角形的面积公式:S=ah÷2,可变形为h=2S÷a,即用440乘2再除以40即可求出高是多少。
【详解】440×2÷40
=880÷40
=22(厘米)
答:高是22厘米。
【点睛】本题考查三角形的面积,熟记公式是解题的关键。
14.1750平方米
【分析】平行四边形的面积=底×高,把底70米,高25米代入公式计算即可求出这块平行四边形菜地的面积。
【详解】70×25=1750(平方米)
答:它的面积是1750平方米。
【点睛】此题考查了平行四边形面积计算公式的应用。计算平行四边形的面积时,底和高一定要相对应。
15.(1)116平方米;(2)4060元
【分析】(1)看图,草坪是由一个长12米、宽5米的长方形和一个上底12米、下底16米、高(9-5)米的梯形组成的。长方形面积=长×宽,梯形面积=(上底+下底)×高÷2,据此列式先分别求出长方形和梯形的面积,再相加即可求出草坪的面积;
(2)将草坪的面积乘35元,求出铺满这个草坪需要多少元。
【详解】(1)12×5+(12+16)×(9-5)÷2
=60+28×4÷2
=60+56
=116(平方米)
答:草坪的面积是116平方米。
(2)116×35=4060(元)
答:铺满这个草坪需要4060元。
【点睛】本题考查了组合图形的面积,将不规则的组合图形分成几个常见图形,分别求常见多边形的面积,再相加即可求出组合图形的面积。
16.166平方米
【分析】观察图形可知,草地的面积=长方形的面积-正方形的面积-梯形的面积,根据长方形的面积=长×宽,正方形的面积=边长×边长,梯形的面积=(上底+下底)×高÷2,代入数据计算即可。
【详解】长方形的面积:
20×10=200(平方米)
正方形的面积:
4×4=16(平方米)
梯形的面积:
(5+7)×3÷2
=12×3÷2
=18(平方米)
草地的面积:
200-16-18=166(平方米)
答:草地的面积是166平方米。
【点睛】本题考查组合图形面积的求法,先分析出组合图形是由哪些图形相加或相减得到,然后根据图形面积公式列式计算。
17.(1)见详解
(2)9平方米
【分析】(1)画出底是0.6米,高是15米的平行四边形道路;
(2)根据平行四边形面积=底×高,求出小路的面积。
【详解】(1)如图所示
(2)(平方米)
答:这条小路的面积是9平方米。
【点睛】本题考查平行四边形的面积,解答本题的关键是掌握平行四边形的面积计算公式。
18.平行四边形;理由见详解
【分析】平行线间的距离处处相等,因此三个图形的高相等,假设高都是h,根据梯形面积=(上底+下底)×高÷2,三角形面积=底×高÷2,平行四边形面积=底×高,分别用字母表示出它们的面积,比较即可。
【详解】假设高都是h。
梯形面积:(6+4)×h÷2=10×h÷2=5h
三角形面积:11×h÷2=5.5h
平行四边形面积:6h
6h>5.5h>5h
答:平行四边形的面积最大。
【点睛】关键是掌握并灵活运用梯形、三角形和平行四边形面积公式。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第2单元多边形的面积重难点应用题专项突破-数学五年级上册苏教版
一、解答题
1.如图所示,李大爷靠墙围了一块菜地,围菜地的篱笆长36m,求这块菜地的面积。
2.某实验小学有一块劳动实践基地(如图)。这块地的面积是多少平方米?
3.有一块平行四边形的苗圃,底是80米,高是40米。如果每平方米种4棵腊梅苗,这个苗圃共种腊梅苗多少棵?
4.一个平行四边形的停车场,底是44米,高是64米,平均每辆车子占地16平方米。
5.“愉快劳动,成果共享”,实验小学利用学校闲置的空地,建起一块“种植园”作为劳动实践基地,形状如下图,这块劳动实践基地的面积是多少平方米?
6.如图,学校要在一块平行四边形的草地中间建造一个梯形的休息区,草地的面积还剩多少?
7.用48米长的篱笆,在靠墙的地方围一块菜地(如图)。这块菜地的面积是多少平方米?如果按照每平方米菜地一年能收入16.5元计算,这块菜地一年能收入多少元?
8.一块三角形玉米地,底是20米,高是15米,共收玉米300千克,平均每平方米收玉米多少千克?
9.植物是制造氧气的“工厂”,根据测算,1平方米的草坪每天能够释放约800克的氧气。
(1)如图,在一块梯形草坪中间有一条宽1米的石子路。这块草坪面积是多少平方米?
(2)这块草坪一个月(30天)大约能释放氧气多少千克?
10.建党100周年之际,某革命教育展览馆计划把原来的等腰梯形展区扩建成一个长方形展区(如图),求展区面积比原来增加了多少平方米?
11.实验小学五年级一班的学生要为学校运动会准备60面红旗,红旗形状为同样大小的直角三角形,每面红旗的两条直角边长分别是32厘米和24厘米。学校为他们准备了一块面积是2平方米的红布,够不够用?如果不够用,至少还需要多少平方厘米红布?
12.一个梯形如果上底增加4厘米,下底和高都不变,它的面积增加12平方厘米;如果高增加4厘米,上、下底都不变,面积增加16平方厘米。原梯形的面积是多少平方厘米?
13.一个三角形硬纸板的面积是440平方厘米,它的底是40厘米,高是多少厘米?
14.一个底是70米,高是25米平行四边形菜地,它的面积是多少平方米?
15.三角洲公园要铺设一块草坪,如图所示。
(1)草坪的面积是多少平方米?
(2)每平方米草坪造价35元,铺满这个草坪需要多少元?
16.新丰学校有一块长方形草地,中间有两个小水池,其余的地方是草地,(如下图)草地的面积是多少平方米?
17.王叔叔家有一块长20米,宽15米的长方形土地,一条底边是0.6米的平行四边形道路从中穿过,把这块土地分成了一个三角形和一个梯形。
(1)请你在图中画出这条小路的位置和形状。
(2)这条小路的面积是多少平方米?
18.小兰在一组平行线之间画了三个图形(如下图),观察三个图形,你觉得哪个图形的面积最大?请说明理由。
参考答案:
1.144平方米
【分析】由图片可知,菜地是一个梯形,上底+下底+高=36米,高=12米,则上底+下底=36-12=24米,梯形面积=(上底+下底)×高÷2,打入数据计算解答。
【详解】(36-12)×12÷2
=24×12÷2
=288÷2
=144(平方米)
答:这块菜地面积是144平方米。
2.64平方米
【分析】如图,将整个实践基地分为两个部分。其中①是一个上底为2米、下底为8米,高为8米的直角梯形;②是一个底为6米、高为8米的直角三角形。可以分别计算出两部分的面积再相加。
【详解】梯形面积:(2+8)×8÷2
=10×8÷2
=80÷2
=40(平方米)
三角形面积:6×8÷2
=48÷2
=24(平方米)
共:40+24=64(平方米)
答:这块地的面积是64平方米。
3.12800棵
【分析】先根据平行四边形的面积=底×高,用80×40求出这个苗圃的面积是3200平方米;每平方米种4棵腊梅苗,求这个苗圃共种的腊梅的棵数,也就是求3200个4是多少,用乘法计算,列式为4×3200。
【详解】4×(80×40)
=4×3200
=12800(棵)
答:这个苗圃共种腊梅苗12800棵。
4.够
【分析】利用平行四边形的面积公式先求出这个停车场的总面积,根据已知平均每辆车子占地16平方米,利用除法即可求得最多可以停放的车辆数。
【详解】44×64÷16
=2816÷16
=176(辆)
176>150可以停放150辆车。
答:这个停车场可以停放150辆车。
5.1330平方米
【分析】观察图形可知,实践基地的面积相当于一个三角形的面积加上一个平行四边形的面积,根据三角形的面积=底×高÷2,用35×12÷2即可求出三角形的面积;再根据平行四边形的面积=底×高,用28×40即可求出平行四边形的面积,然后将两部分相加即可。
【详解】35×12÷2=210(平方米)
28×40=1120(平方米)
210+1120=1330(平方米)
答:这块劳动实践基地的面积是1330平方米。
6.160平方米
【分析】观察图形可知,用平行四边形草地的面积减去梯形休息区的面积即可求出草地剩下的面积。平行四边形的面积=底×高,梯形的面积=(上底+下底)×高÷2,据此解答。
【详解】18×10-(3+7)×4÷2
=180-10×4÷2
=180-20
=160(平方米)
答:草地的面积还剩160平方米。
7.4752元
【分析】根据对图的观察,该菜地为一个直角梯形,48米篱笆的长度为该梯形的上底、下底和高的和,高为24米,用48减24,可求出该梯形菜地的上底与下底的和,根据梯形面积公式:S=(上底+下底)×高÷2,代入数据求出该菜地的面积,最后乘16.5,即可求出这个菜地一年的收入有多少元。
【详解】由分析可知:
(48-24)×24÷2
=24×24÷2
=576÷2
=288(平方米)
288×16.5=4752(元)
答:这块菜地的面积是288平方米,这块菜地一年能收入4752元。
【点睛】本题考查了梯形面积公式的应用,熟记公式是解题的关键。
8.2千克
【分析】根据三角形的面积公式:S=ah÷2,据此求出玉米地的面积;再根据除法的意义,用收玉米的重量除以玉米地的面积即可求出平均每平方米收玉米多少千克。
【详解】20×15÷2
=300÷2
=150(平方米)
300÷150=2(千克)
答:平均每平方米收玉米2千克。
9.(1)1470平方米
(2)35280千克
【分析】(1)观察图形可知,草坪的面积=梯形的面积-平行四边形的面积;根据梯形的面积=(上底+下底)×高÷2,平行四边形的面积=底×高,代入数据计算求解。
(2)已知1平方米的草坪每天能够释放约800克的氧气,根据进率“1千克=1000克”,把800克换算成0.8千克;
用1平方米的草坪每天释放氧气的质量乘草坪的面积,求出这块草坪每天释放氧气的质量,再乘30,即是这块草坪一个月(30天)大约能释放氧气的质量。
【详解】(1)梯形的面积:
(36+50)×35÷2
=86×35÷2
=3010÷2
=1505(平方米)
平行四边形的面积:1×35=35(平方米)
草坪的面积:1505-35=1470(平方米)
答:这块草坪面积是1470平方米。
(2)800克=0.8千克
0.8×1470×30
=1176×30
=35280(千克)
答:这块草坪一个月(30天)大约能释放氧气35280千克。
10.425平方米
【分析】先根据长方形的面积=长×宽,用62×25求出长方形的面积;再根据梯形的面积=(上底+下底)×高÷2,用(28+62)×25÷2求出梯形的面积;最后用长方形的面积减去梯形的面积,即可求出展区面积比原来增加了多少平方米。
【详解】62×25-(28+62)×25÷2
=1550-90×25÷2
=1550-2250÷2
=1550-1125
=425(平方米)
答:展区面积比原来增加了425平方米。
11.3040平方厘米
【分析】先根据三角形的面积=底×高÷2,代入数据求出每面红旗的面积;再乘60,求出做60块红旗需要的红布的总面积;然后根据1平方米=10000平方厘米,高级单位转化为低级单位乘进率,将2平方米换算成20000平方厘米,与做60块红旗需要的红布的总面积比较大下后求差即可。
【详解】32×24÷2×60
=768÷2×60
=384×60
=23040(平方厘米)
2平方米=20000平方厘米
23040>20000
23040-20000=3040(平方厘米)
答:至少还需要3040平方厘米红布。
【点睛】解答本题需熟练掌握三角形的面积公式,明确面积单位之间的进率。
12.24平方厘米
【分析】已知一个梯形的下底和高都不变,如果上底增加4厘米,面积增加12平方厘米,增加的是一个底为4厘米,高等于原梯形的高的三角形;根据三角形的高=三角形的面积×2÷底,即可求出三角形的高,也就是原梯形的高;
已知这个梯形的上、下底都不变,如果高增加4厘米,面积增加16平方厘米;根据梯形的上、下底之和=梯形的面积×2÷高,由此求出原梯形的上、下底之和;
最后根据梯形的面积=(上底+下底)×高÷2,代入数据计算,即可求出原梯形的面积。
【详解】原梯形的高:
12×2÷4
=24÷4
=6(厘米)
原梯形上、下底之和:
16×2÷4
=32÷4
=8(厘米)
原梯形的面积:
8×6÷2
=48÷2
=24(平方厘米)
答:原梯形的面积是24平方厘米。
【点睛】本题考查梯形面积、三角形面积公式的灵活运用,求出原梯形的高与上、下底之和是解题的关键。
13.22厘米
【分析】根据三角形的面积公式:S=ah÷2,可变形为h=2S÷a,即用440乘2再除以40即可求出高是多少。
【详解】440×2÷40
=880÷40
=22(厘米)
答:高是22厘米。
【点睛】本题考查三角形的面积,熟记公式是解题的关键。
14.1750平方米
【分析】平行四边形的面积=底×高,把底70米,高25米代入公式计算即可求出这块平行四边形菜地的面积。
【详解】70×25=1750(平方米)
答:它的面积是1750平方米。
【点睛】此题考查了平行四边形面积计算公式的应用。计算平行四边形的面积时,底和高一定要相对应。
15.(1)116平方米;(2)4060元
【分析】(1)看图,草坪是由一个长12米、宽5米的长方形和一个上底12米、下底16米、高(9-5)米的梯形组成的。长方形面积=长×宽,梯形面积=(上底+下底)×高÷2,据此列式先分别求出长方形和梯形的面积,再相加即可求出草坪的面积;
(2)将草坪的面积乘35元,求出铺满这个草坪需要多少元。
【详解】(1)12×5+(12+16)×(9-5)÷2
=60+28×4÷2
=60+56
=116(平方米)
答:草坪的面积是116平方米。
(2)116×35=4060(元)
答:铺满这个草坪需要4060元。
【点睛】本题考查了组合图形的面积,将不规则的组合图形分成几个常见图形,分别求常见多边形的面积,再相加即可求出组合图形的面积。
16.166平方米
【分析】观察图形可知,草地的面积=长方形的面积-正方形的面积-梯形的面积,根据长方形的面积=长×宽,正方形的面积=边长×边长,梯形的面积=(上底+下底)×高÷2,代入数据计算即可。
【详解】长方形的面积:
20×10=200(平方米)
正方形的面积:
4×4=16(平方米)
梯形的面积:
(5+7)×3÷2
=12×3÷2
=18(平方米)
草地的面积:
200-16-18=166(平方米)
答:草地的面积是166平方米。
【点睛】本题考查组合图形面积的求法,先分析出组合图形是由哪些图形相加或相减得到,然后根据图形面积公式列式计算。
17.(1)见详解
(2)9平方米
【分析】(1)画出底是0.6米,高是15米的平行四边形道路;
(2)根据平行四边形面积=底×高,求出小路的面积。
【详解】(1)如图所示
(2)(平方米)
答:这条小路的面积是9平方米。
【点睛】本题考查平行四边形的面积,解答本题的关键是掌握平行四边形的面积计算公式。
18.平行四边形;理由见详解
【分析】平行线间的距离处处相等,因此三个图形的高相等,假设高都是h,根据梯形面积=(上底+下底)×高÷2,三角形面积=底×高÷2,平行四边形面积=底×高,分别用字母表示出它们的面积,比较即可。
【详解】假设高都是h。
梯形面积:(6+4)×h÷2=10×h÷2=5h
三角形面积:11×h÷2=5.5h
平行四边形面积:6h
6h>5.5h>5h
答:平行四边形的面积最大。
【点睛】关键是掌握并灵活运用梯形、三角形和平行四边形面积公式。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
