北师大版 六年级上册数学6.3.比的应用 课件(共33张PPT)
文档属性
| 名称 | 北师大版 六年级上册数学6.3.比的应用 课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-18 07:28:58 | ||
图片预览











文档简介
(共33张PPT)
把下面各比化成最简单的整数比。
36︰48
= 3︰4
0.24︰0.6
=2︰5
0.625︰
= (36÷12)∶(48÷12)
=(0.24×100)∶(0.6×100)
=24∶60
= (24÷12)∶(60÷12)
复习:
把下面各比化成最简单的整数比。
= 25︰28
=5︰6
0.625︰
=∶
=∶
=∶
复习:
六年级班男生人数与女生人数的比是5 ∶4 ∶5。
可以把男生人数看作( )份,女生人数有( )份。全班共有( )份。
女生人数是男生人数的( ),
男生人数是女生人数的( ),
女生人数是全班总人数的( ),
男生人数是全班总人数的( )。
5
4
9
复习旧知:
第六单元 比的认识
比的应用
(按比例分配)
小学 / 数学 / 北师大版 / 六年级上册
情境导入:
你能帮她分一分吗?
情境导入:
如果是你,你会怎么分呢?
两个班级人数不一定相等,如果将这些橘子平均分给两个班级不太合适。
情境导入:
如果是你,你会怎么分呢?
应该按照两个班级人数的比例分更合适。
探究新知:
关键是橘子的总数也不知道呀?
如果一共有50个橘子,能否一班分30个,二班分20个?
探究新知:
第一种:平均分。
哪种分法合理呢?为什么?
第二种:按班级人数比例分。
探究新知:
由于1班与2班的人数不同,按照人数的比来分配较为合理。
1班和2班的人数比是多少呢?
1班
30
2班
20
:
= 3 ∶ 2
探究新知:
如果有140个橘子,按3:2的比例分,应该怎么分?
140个
一班
二班
1班:28×3=84(个)
一份:140 ÷(3+2)=28(个)
2班:28×2=56(个)
探究新知:
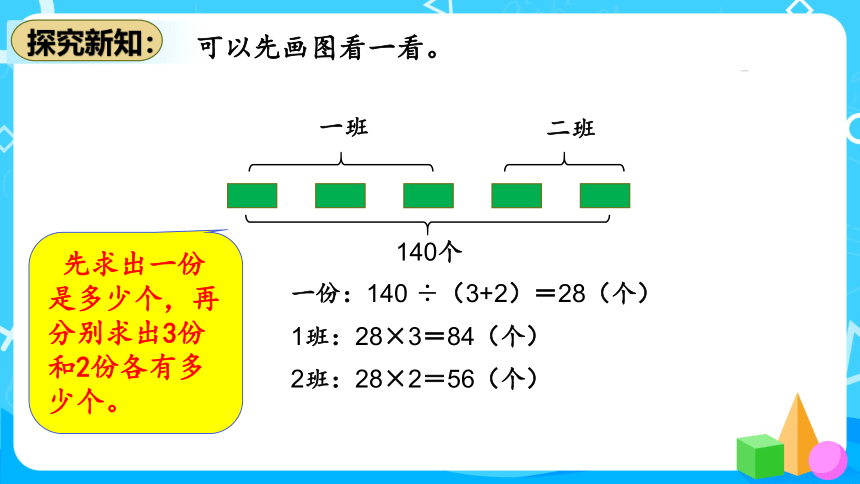
可以先画图看一看。
先求出一份是多少个,再分别求出3份和2份各有多少个。
140个
3 + 2 = 5(份)
探究新知:
可以先画图看一看。
先求出一共有几份,再求出两个班分别占总数的几分之几。
1班:140 x =84(个)
2班:140 x =56(个)
一班
二班
还可以这样写:
140个
一班
二班
探究新知:
可以先画图看一看。
比的意义:3+2=5
140÷5=28(个)
分数的意义:3+2=5
答:1班分到84个,2班分到56个。
等量关系是:
3份(1班)+2份(2班)=140个
解:设每份橘子是 个,那么1班3 个,2班2 个。
3 +2 =140
5 =140
=28
3 =3×28=84(个)
2 =2×28=56(个)
答:1班分到84个,2班分到56个。
探究新知:
如果有140个橘子,按3:2的比例分,应该怎么分?
也可以用方程解答:
注意:求出x的值后,还要计算出3x和2x的值分别是多少。
140个
一班占总数的
3
5
二班占总数的
2
5
探究新知:
可以先画图看一看。
常用的解答格式:
1班:140 x =84(个)
2班:140 x =56(个)
答:1班分到84个,2班分到56个。
一座水库按2∶3放养鲢鱼和鲤鱼,一共可以放养育苗25000尾。其中鲢鱼和鲤鱼的鱼苗各应放养多少尾?
2+3=5
25000× =10000(尾)
2
5
25000× =15000(尾)
3
5
课堂练习:
答:鲢鱼放养10000尾,鲤鱼放养15000尾。
和平小学共有师生1200人,老师和学生的
人数比是1 ∶19,老师和学生各有多少人?
老师:60×1=60(人)
1200 ÷(1+19)=60(人)
学生:60×19=1140(人)
课堂练习:
答:老师有60人,学生有1140人。
1+19=20
1200× =60(人)
1200× =1140(人)
440g
探究新知:
调制巧克力奶,巧克力与牛奶的质量比是2 ∶9。淘气有巧克力440g,都用来调巧克力奶。他要准备多少克牛奶?
440g
9份
一份:440÷2=220(克)
九份:220×9=1980(克)
答:他要准备1980克奶。
?g
方法一:
探究新知:
调制巧克力奶,巧克力与牛奶的质量比是2 ∶9。淘气有巧克力440g,都用来调巧克力奶。他要准备多少克牛奶?
可以先求出一份是多少,再求出9份是多少。
440g
2份
答:他要准备1980克奶。
440÷ =1980(克)
440g
9份
?g
方法二:
探究新知:
调制巧克力奶,巧克力与牛奶的质量比是2 ∶9。淘气有巧克力440g,都用来调巧克力奶。他要准备多少克牛奶?
可以把奶看作单位“1”,用“量率对应”的思想解答。
440g
2份
280g
280÷2=140(克)
140×(2+9)=1540(克)
答:她能调制出1540克巧克力奶。
?g
(2+9)份
笑笑有巧克力280g,也都用来调巧克力奶。她能调制出多少克巧克力奶?
方法一:
课堂练习:
(巧克力与牛奶的质量比是2 ∶9)
280g
(2+9)份
答:她能调制出1540克巧克力奶。
280÷1540(克)
方法二:
探究新知:
笑笑有巧克力280g,也都用来调巧克力奶。她能调制出多少克巧克力奶?
可以把巧克力奶看作单位“1”,用“量率对应”的思想解答。
(巧克力与牛奶的质量比是2 ∶9)
六⑴班和六⑵班订《少年科学》的人数比是3∶4,六⑴班有21人订,两个班一共有多少人订?
3+4=7
21÷3×7=49(人)
方法一:
方法二:
21÷=49(人)
答:两个班一共有49人订。
课堂练习:
⑴成年人的身高与脚长的比一般是7∶1,王叔叔身高是1.8m,他的脚长大约是多少?(结果保留两位小数)
1.8÷7×1≈0.26(m)
答:他的脚长大约是0.26m。
课堂练习:
⑵成年人血液的质量与体重之比大约是1∶13,李叔叔的体重是65kg,他身体里的血液有多少千克?
65÷13×1=5(kg)
答:他身体里的血液有5千克。
一种喷洒庄稼的药水,农药和水的质量比1∶150,现有3kg农药,需要加多少千克水?
3×150=450(kg)
答:需要加450千克水。
课堂练习:
一种什锦糖是由奶糖、水果糖和酥糖按2∶4∶3混合成的,要配制这样的什锦糖450kg,三种糖各需多少千克?
奶糖:450×=100(kg)
2+4+3=9
答:需要奶糖100千克、水果糖200千克和酥糖150千克。
水果糖:450×=200(kg)
酥糖:450×=150(kg)
课堂练习:
甲、乙两数的平均数是56,甲与乙的比是4∶3。甲、乙各是多少?
先求出比所对应的总量:
答:甲数是64,乙数是48。
4+3=7
课堂练习:
按比例分配,分配的是比所对应的总量。
56×2=112
112×=64
然后按比例分配:
112×=48
方法二:
答:甲数是64,乙数是48。
56×2=112
甲、乙两数的平均数是56,甲与乙的比是4∶3。甲、乙各是多少?
课堂练习:
先求出比所对应的总量:
甲:16×4=64
112÷(3+4)=16
乙:16×3=48
再求出一份是多少:
最后求出甲乙分别是多少:
(1)图书室里连环画和文艺书的数量比是2:5,文艺书有90本,连环画有( )本。
(2)一本故事书,小华已读了24页。已知他已读的和未读的页数比是3:8,这本书一共( )页。
(3)王爷爷家养了一些鸡和鸭,鸡和鸭数量的比是3:5。如果鸡比鸭少40只,那么鸡有( )只。
(5)甲、乙、丙三个数的比是3:4:8,它们的和是60,甲数是( )。
课堂练习:
36
88
60
12
两个长方形重叠部分的面积相当于大长方形面积的,相当于小长方形面积的,大长方形和小长方形面积的比是多少?
小长方形面积是重叠部分的4倍。
大长方形面积是重叠部分的6倍。
大长方形和小长方形面积的比是3∶2。
3∶2
6∶4=
课堂练习:
方法一:画图分析
两个长方形重叠部分的面积相当于大长方形面积的,相当于小长方形面积的,大长方形和小长方形面积的比是多少?
1
大长方形和小长方形面积的比是3∶2。
3∶2
面积比=6∶4=
课堂练习:
方法二:把阴影部分看做1,列式计算:
大长方形:
小长方形:
布置作业:
练习册
54页1--4题和55页1--4题。
把下面各比化成最简单的整数比。
36︰48
= 3︰4
0.24︰0.6
=2︰5
0.625︰
= (36÷12)∶(48÷12)
=(0.24×100)∶(0.6×100)
=24∶60
= (24÷12)∶(60÷12)
复习:
把下面各比化成最简单的整数比。
= 25︰28
=5︰6
0.625︰
=∶
=∶
=∶
复习:
六年级班男生人数与女生人数的比是5 ∶4 ∶5。
可以把男生人数看作( )份,女生人数有( )份。全班共有( )份。
女生人数是男生人数的( ),
男生人数是女生人数的( ),
女生人数是全班总人数的( ),
男生人数是全班总人数的( )。
5
4
9
复习旧知:
第六单元 比的认识
比的应用
(按比例分配)
小学 / 数学 / 北师大版 / 六年级上册
情境导入:
你能帮她分一分吗?
情境导入:
如果是你,你会怎么分呢?
两个班级人数不一定相等,如果将这些橘子平均分给两个班级不太合适。
情境导入:
如果是你,你会怎么分呢?
应该按照两个班级人数的比例分更合适。
探究新知:
关键是橘子的总数也不知道呀?
如果一共有50个橘子,能否一班分30个,二班分20个?
探究新知:
第一种:平均分。
哪种分法合理呢?为什么?
第二种:按班级人数比例分。
探究新知:
由于1班与2班的人数不同,按照人数的比来分配较为合理。
1班和2班的人数比是多少呢?
1班
30
2班
20
:
= 3 ∶ 2
探究新知:
如果有140个橘子,按3:2的比例分,应该怎么分?
140个
一班
二班
1班:28×3=84(个)
一份:140 ÷(3+2)=28(个)
2班:28×2=56(个)
探究新知:
可以先画图看一看。
先求出一份是多少个,再分别求出3份和2份各有多少个。
140个
3 + 2 = 5(份)
探究新知:
可以先画图看一看。
先求出一共有几份,再求出两个班分别占总数的几分之几。
1班:140 x =84(个)
2班:140 x =56(个)
一班
二班
还可以这样写:
140个
一班
二班
探究新知:
可以先画图看一看。
比的意义:3+2=5
140÷5=28(个)
分数的意义:3+2=5
答:1班分到84个,2班分到56个。
等量关系是:
3份(1班)+2份(2班)=140个
解:设每份橘子是 个,那么1班3 个,2班2 个。
3 +2 =140
5 =140
=28
3 =3×28=84(个)
2 =2×28=56(个)
答:1班分到84个,2班分到56个。
探究新知:
如果有140个橘子,按3:2的比例分,应该怎么分?
也可以用方程解答:
注意:求出x的值后,还要计算出3x和2x的值分别是多少。
140个
一班占总数的
3
5
二班占总数的
2
5
探究新知:
可以先画图看一看。
常用的解答格式:
1班:140 x =84(个)
2班:140 x =56(个)
答:1班分到84个,2班分到56个。
一座水库按2∶3放养鲢鱼和鲤鱼,一共可以放养育苗25000尾。其中鲢鱼和鲤鱼的鱼苗各应放养多少尾?
2+3=5
25000× =10000(尾)
2
5
25000× =15000(尾)
3
5
课堂练习:
答:鲢鱼放养10000尾,鲤鱼放养15000尾。
和平小学共有师生1200人,老师和学生的
人数比是1 ∶19,老师和学生各有多少人?
老师:60×1=60(人)
1200 ÷(1+19)=60(人)
学生:60×19=1140(人)
课堂练习:
答:老师有60人,学生有1140人。
1+19=20
1200× =60(人)
1200× =1140(人)
440g
探究新知:
调制巧克力奶,巧克力与牛奶的质量比是2 ∶9。淘气有巧克力440g,都用来调巧克力奶。他要准备多少克牛奶?
440g
9份
一份:440÷2=220(克)
九份:220×9=1980(克)
答:他要准备1980克奶。
?g
方法一:
探究新知:
调制巧克力奶,巧克力与牛奶的质量比是2 ∶9。淘气有巧克力440g,都用来调巧克力奶。他要准备多少克牛奶?
可以先求出一份是多少,再求出9份是多少。
440g
2份
答:他要准备1980克奶。
440÷ =1980(克)
440g
9份
?g
方法二:
探究新知:
调制巧克力奶,巧克力与牛奶的质量比是2 ∶9。淘气有巧克力440g,都用来调巧克力奶。他要准备多少克牛奶?
可以把奶看作单位“1”,用“量率对应”的思想解答。
440g
2份
280g
280÷2=140(克)
140×(2+9)=1540(克)
答:她能调制出1540克巧克力奶。
?g
(2+9)份
笑笑有巧克力280g,也都用来调巧克力奶。她能调制出多少克巧克力奶?
方法一:
课堂练习:
(巧克力与牛奶的质量比是2 ∶9)
280g
(2+9)份
答:她能调制出1540克巧克力奶。
280÷1540(克)
方法二:
探究新知:
笑笑有巧克力280g,也都用来调巧克力奶。她能调制出多少克巧克力奶?
可以把巧克力奶看作单位“1”,用“量率对应”的思想解答。
(巧克力与牛奶的质量比是2 ∶9)
六⑴班和六⑵班订《少年科学》的人数比是3∶4,六⑴班有21人订,两个班一共有多少人订?
3+4=7
21÷3×7=49(人)
方法一:
方法二:
21÷=49(人)
答:两个班一共有49人订。
课堂练习:
⑴成年人的身高与脚长的比一般是7∶1,王叔叔身高是1.8m,他的脚长大约是多少?(结果保留两位小数)
1.8÷7×1≈0.26(m)
答:他的脚长大约是0.26m。
课堂练习:
⑵成年人血液的质量与体重之比大约是1∶13,李叔叔的体重是65kg,他身体里的血液有多少千克?
65÷13×1=5(kg)
答:他身体里的血液有5千克。
一种喷洒庄稼的药水,农药和水的质量比1∶150,现有3kg农药,需要加多少千克水?
3×150=450(kg)
答:需要加450千克水。
课堂练习:
一种什锦糖是由奶糖、水果糖和酥糖按2∶4∶3混合成的,要配制这样的什锦糖450kg,三种糖各需多少千克?
奶糖:450×=100(kg)
2+4+3=9
答:需要奶糖100千克、水果糖200千克和酥糖150千克。
水果糖:450×=200(kg)
酥糖:450×=150(kg)
课堂练习:
甲、乙两数的平均数是56,甲与乙的比是4∶3。甲、乙各是多少?
先求出比所对应的总量:
答:甲数是64,乙数是48。
4+3=7
课堂练习:
按比例分配,分配的是比所对应的总量。
56×2=112
112×=64
然后按比例分配:
112×=48
方法二:
答:甲数是64,乙数是48。
56×2=112
甲、乙两数的平均数是56,甲与乙的比是4∶3。甲、乙各是多少?
课堂练习:
先求出比所对应的总量:
甲:16×4=64
112÷(3+4)=16
乙:16×3=48
再求出一份是多少:
最后求出甲乙分别是多少:
(1)图书室里连环画和文艺书的数量比是2:5,文艺书有90本,连环画有( )本。
(2)一本故事书,小华已读了24页。已知他已读的和未读的页数比是3:8,这本书一共( )页。
(3)王爷爷家养了一些鸡和鸭,鸡和鸭数量的比是3:5。如果鸡比鸭少40只,那么鸡有( )只。
(5)甲、乙、丙三个数的比是3:4:8,它们的和是60,甲数是( )。
课堂练习:
36
88
60
12
两个长方形重叠部分的面积相当于大长方形面积的,相当于小长方形面积的,大长方形和小长方形面积的比是多少?
小长方形面积是重叠部分的4倍。
大长方形面积是重叠部分的6倍。
大长方形和小长方形面积的比是3∶2。
3∶2
6∶4=
课堂练习:
方法一:画图分析
两个长方形重叠部分的面积相当于大长方形面积的,相当于小长方形面积的,大长方形和小长方形面积的比是多少?
1
大长方形和小长方形面积的比是3∶2。
3∶2
面积比=6∶4=
课堂练习:
方法二:把阴影部分看做1,列式计算:
大长方形:
小长方形:
布置作业:
练习册
54页1--4题和55页1--4题。
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
