2024-2025学年云南省曲靖市富源县多校高二上学期开学考试数学试题(含答案)
文档属性
| 名称 | 2024-2025学年云南省曲靖市富源县多校高二上学期开学考试数学试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 144.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-18 00:00:00 | ||
图片预览



文档简介
2024-2025学年云南省曲靖市富源县多校高二上学期开学考试
数学试题
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知,,则( )
A. B. C. D.
2.命题“”的否定是( )
A. B.
C. D.
3.已知复数其中为虚数单位,则复数在复平面内对应的点位于 .
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
4.已知角的顶点与坐标原点重合,始边与轴正半轴重合,终边落在直线上,则 .
A. B. C. D.
5.某高中的三个年级共有学生人,其中高一人,高二人,高三人,该校现在要了解学生对校本课程的看法,准备从全校学生中抽取人进行访谈,若采取按比例分配的分层抽样,且按年级来分层,则高一年级应抽取的人数是( )
A. B. C. D.
6.已知,是两条不同的直线,,是两个不同的平面,下列说法正确的是( )
A. 若,,则 B. 若,,则
C. 若,,则 D. 若,,则
7.一枚质地均匀的正方体骰子,其六个面分别刻有,,,,,六个数字,投掷这枚骰子两次,事件“第一次向上一面的数字是”,事件“第二次向上一面的数字是”,事件“两次向上一面的数字之和是”,事件“两次向上一面的数字之和是”,则( )
A. 与相互独立 B. 与相互独立 C. 与相互独立 D. 与相互独立
8.我国古代数学家赵爽创制了一幅“勾股圆方图”,后人称为“赵爽弦图”他用数形结合的方法给出了勾股定理的证明,极富创新意识“赵爽弦图”是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形如图,若大正方形的面积是,小正方形的面积是,则( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知甲种杂交水稻近五年的产量单位:吨公顷数据为:,,,,,乙种杂交水稻近五年的产量单位:吨公顷数据为:,,,,,则( )
A. 甲种的样本平均数等于乙种的样本平均数
B. 甲种的样本方差大于乙种的样本方差
C. 甲种样本的分位数小于乙种样本的分位数
D. 甲乙两种水稻近五年的总方差为
10.已知圆锥的顶点为,底面圆心为,为底面直径,,,点在底面圆周上,且二面角为,则 .
A. 该圆锥的体积为 B. 该圆锥的侧面积为
C. D. 的面积为
11.在中,内角所对的边分别为,其中,且,则下列说法正确的是( )
A.
B. 面积的最大值为
C. 若为边的中点,则的最大值为
D. 若为锐角三角形,则其周长的取值范围为
三、填空题:本题共3小题,每小题5分,共15分。
12.已知向量,,则在方向上的投影向量为 .
13.已知函数和,其中、均可取、、、、、中的任一数则这两函数图象有交点的概率为 .
14.已知是单位向量,且,则向量与的夹角为 .
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
在中,内角的对边分别为,向量且.
求角;
若,求内切圆的半径.
16.本小题分
如图,在四棱锥中,底面是正方形,平面,且,点为线段的中点.
求证:平面;
求证:平面;
17.本小题分
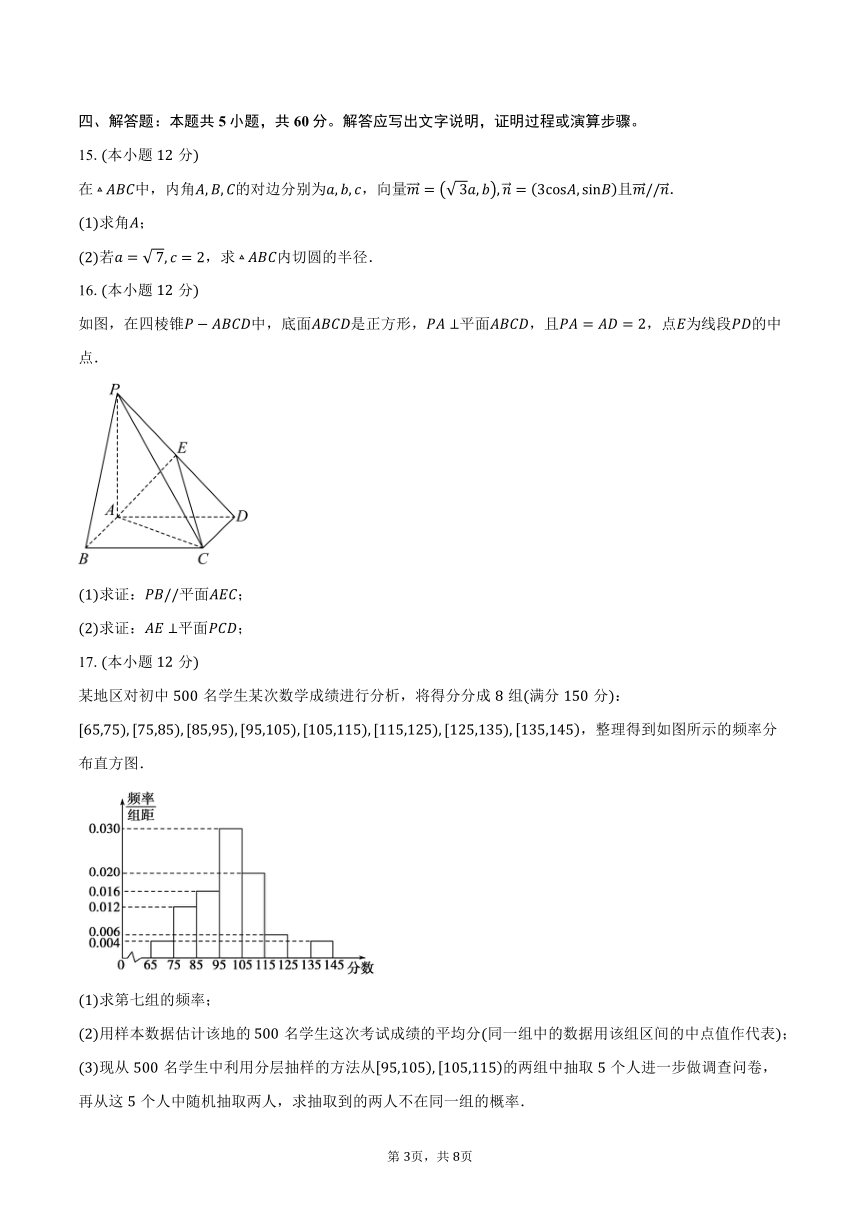
某地区对初中名学生某次数学成绩进行分析,将得分分成组满分分:,整理得到如图所示的频率分布直方图.
求第七组的频率;
用样本数据估计该地的名学生这次考试成绩的平均分同一组中的数据用该组区间的中点值作代表;
现从名学生中利用分层抽样的方法从的两组中抽取个人进一步做调查问卷,再从这个人中随机抽取两人,求抽取到的两人不在同一组的概率.
18.本小题分
设函数.
求的图象的对称轴方程和对称中心的坐标;
求在上的最值.
19.本小题分
如图,四棱锥的底面是边长为的菱形,底面,,,分别是的中点,.
求四棱锥的体积;
求与底面所成角的正切值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:因为向量与平行,所以,
由正弦定理得,
又,所以,所以,
又,所以.
由余弦定理得,所以,解得或舍,
所以的面积,
设内切圆的半径为,
所以,解得.
16.解:
连接,交于点,连接,
是正方形对角线交点,为的中点,
由已知为线段的中点,,
又平面,平面,
平面;
,为线段的中点,,
平面,平面,,
在正方形中,,又,平面,
平面,又平面,
,又,平面,
平面;
17.解:由频率分布直方图得第七组的频率为:
;
用样本数据估计该地名学生这次考试成绩的平均分为:
分;
由频率分步直方图可知 的频数为 的频数为 ,所以两组人数比值为 ,
按照分层抽样抽取人,则在 分别抽取人和人,
记 这组三人的编号为 这组两人的编号为 ,
故从人随机抽取名,共种情况,为:
设事件 “从个人中随机抽取两人,抽取到的两人不在同一组”
则 ,共种情况.
故 ,即从这个人中随机抽取两人,
则抽取到的两人不在同一组的概率为 .
18.解:因为,
令,解得,
所以的对称轴方程为,
令,得,
可得函数图象的对称中心的坐标为;
因为,所以,
令,解得,
所以在上单调递减,在上单调递增,
所以,,,故.
19.解:,,四边形为菱形,
,
,
如图,连,相交于点,连.
,,
,
平面,
平面,且.
;
平面,
与底面形成的角为.
,,
.
故与底面所成角的正切值为.
第1页,共1页
数学试题
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知,,则( )
A. B. C. D.
2.命题“”的否定是( )
A. B.
C. D.
3.已知复数其中为虚数单位,则复数在复平面内对应的点位于 .
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
4.已知角的顶点与坐标原点重合,始边与轴正半轴重合,终边落在直线上,则 .
A. B. C. D.
5.某高中的三个年级共有学生人,其中高一人,高二人,高三人,该校现在要了解学生对校本课程的看法,准备从全校学生中抽取人进行访谈,若采取按比例分配的分层抽样,且按年级来分层,则高一年级应抽取的人数是( )
A. B. C. D.
6.已知,是两条不同的直线,,是两个不同的平面,下列说法正确的是( )
A. 若,,则 B. 若,,则
C. 若,,则 D. 若,,则
7.一枚质地均匀的正方体骰子,其六个面分别刻有,,,,,六个数字,投掷这枚骰子两次,事件“第一次向上一面的数字是”,事件“第二次向上一面的数字是”,事件“两次向上一面的数字之和是”,事件“两次向上一面的数字之和是”,则( )
A. 与相互独立 B. 与相互独立 C. 与相互独立 D. 与相互独立
8.我国古代数学家赵爽创制了一幅“勾股圆方图”,后人称为“赵爽弦图”他用数形结合的方法给出了勾股定理的证明,极富创新意识“赵爽弦图”是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形如图,若大正方形的面积是,小正方形的面积是,则( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知甲种杂交水稻近五年的产量单位:吨公顷数据为:,,,,,乙种杂交水稻近五年的产量单位:吨公顷数据为:,,,,,则( )
A. 甲种的样本平均数等于乙种的样本平均数
B. 甲种的样本方差大于乙种的样本方差
C. 甲种样本的分位数小于乙种样本的分位数
D. 甲乙两种水稻近五年的总方差为
10.已知圆锥的顶点为,底面圆心为,为底面直径,,,点在底面圆周上,且二面角为,则 .
A. 该圆锥的体积为 B. 该圆锥的侧面积为
C. D. 的面积为
11.在中,内角所对的边分别为,其中,且,则下列说法正确的是( )
A.
B. 面积的最大值为
C. 若为边的中点,则的最大值为
D. 若为锐角三角形,则其周长的取值范围为
三、填空题:本题共3小题,每小题5分,共15分。
12.已知向量,,则在方向上的投影向量为 .
13.已知函数和,其中、均可取、、、、、中的任一数则这两函数图象有交点的概率为 .
14.已知是单位向量,且,则向量与的夹角为 .
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
在中,内角的对边分别为,向量且.
求角;
若,求内切圆的半径.
16.本小题分
如图,在四棱锥中,底面是正方形,平面,且,点为线段的中点.
求证:平面;
求证:平面;
17.本小题分
某地区对初中名学生某次数学成绩进行分析,将得分分成组满分分:,整理得到如图所示的频率分布直方图.
求第七组的频率;
用样本数据估计该地的名学生这次考试成绩的平均分同一组中的数据用该组区间的中点值作代表;
现从名学生中利用分层抽样的方法从的两组中抽取个人进一步做调查问卷,再从这个人中随机抽取两人,求抽取到的两人不在同一组的概率.
18.本小题分
设函数.
求的图象的对称轴方程和对称中心的坐标;
求在上的最值.
19.本小题分
如图,四棱锥的底面是边长为的菱形,底面,,,分别是的中点,.
求四棱锥的体积;
求与底面所成角的正切值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:因为向量与平行,所以,
由正弦定理得,
又,所以,所以,
又,所以.
由余弦定理得,所以,解得或舍,
所以的面积,
设内切圆的半径为,
所以,解得.
16.解:
连接,交于点,连接,
是正方形对角线交点,为的中点,
由已知为线段的中点,,
又平面,平面,
平面;
,为线段的中点,,
平面,平面,,
在正方形中,,又,平面,
平面,又平面,
,又,平面,
平面;
17.解:由频率分布直方图得第七组的频率为:
;
用样本数据估计该地名学生这次考试成绩的平均分为:
分;
由频率分步直方图可知 的频数为 的频数为 ,所以两组人数比值为 ,
按照分层抽样抽取人,则在 分别抽取人和人,
记 这组三人的编号为 这组两人的编号为 ,
故从人随机抽取名,共种情况,为:
设事件 “从个人中随机抽取两人,抽取到的两人不在同一组”
则 ,共种情况.
故 ,即从这个人中随机抽取两人,
则抽取到的两人不在同一组的概率为 .
18.解:因为,
令,解得,
所以的对称轴方程为,
令,得,
可得函数图象的对称中心的坐标为;
因为,所以,
令,解得,
所以在上单调递减,在上单调递增,
所以,,,故.
19.解:,,四边形为菱形,
,
,
如图,连,相交于点,连.
,,
,
平面,
平面,且.
;
平面,
与底面形成的角为.
,,
.
故与底面所成角的正切值为.
第1页,共1页
同课章节目录
