第十三章 全等三角形 单元测试题(含答案) 2024-2025学年人教版八年级数学上册
文档属性
| 名称 | 第十三章 全等三角形 单元测试题(含答案) 2024-2025学年人教版八年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 531.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-19 00:00:00 | ||
图片预览



文档简介
第十三章 全等三角形 单元测试题 2024-2025学年人教版八年级数学上册
一、单选题
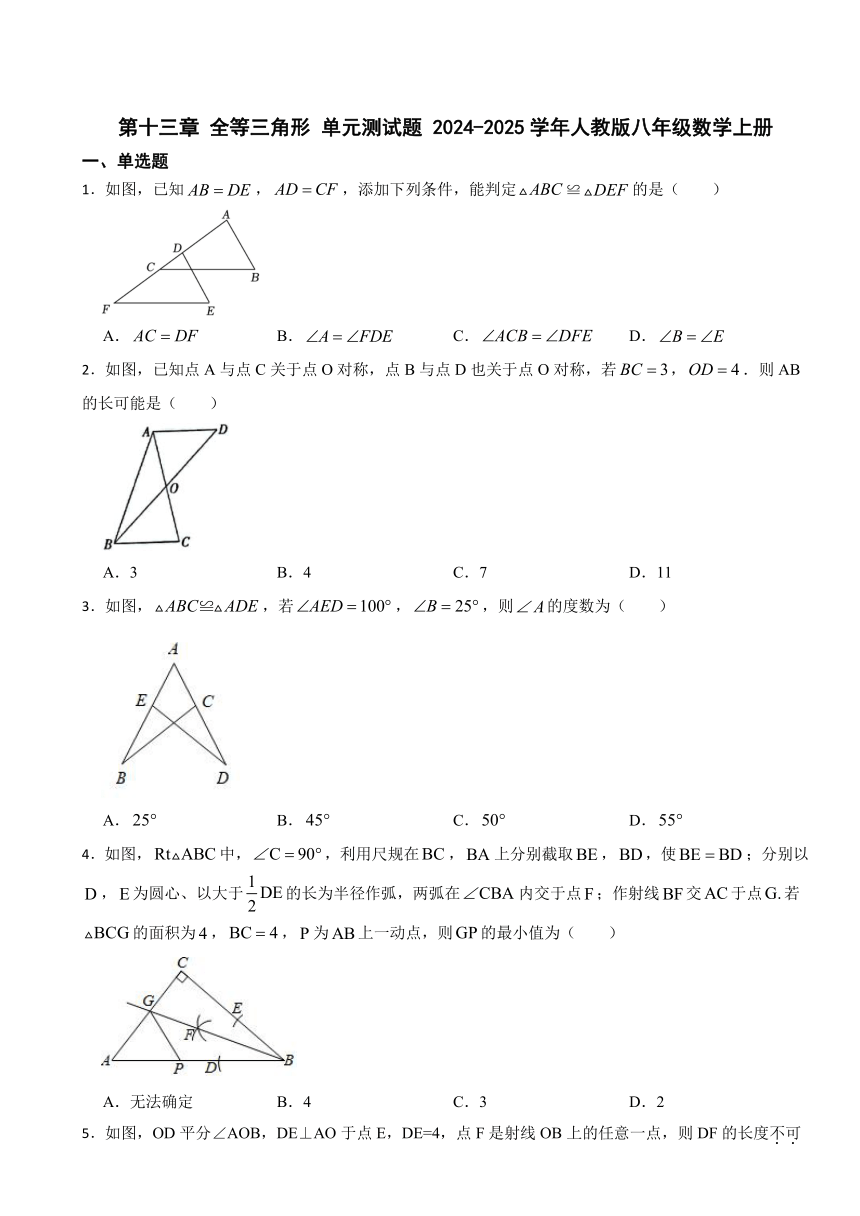
1.如图,已知,,添加下列条件,能判定≌的是( )
A. B. C. D.
2.如图,已知点A与点C关于点O对称,点B与点D也关于点O对称,若,.则AB的长可能是( )
A.3 B.4 C.7 D.11
3.如图,,若,,则的度数为( )
A. B. C. D.
4.如图,中,,利用尺规在,上分别截取,,使;分别以,为圆心、以大于的长为半径作弧,两弧在内交于点;作射线交于点若的面积为,,为上一动点,则的最小值为( )
A.无法确定 B.4 C.3 D.2
5.如图,OD平分∠AOB,DE⊥AO于点E,DE=4,点F是射线OB上的任意一点,则DF的长度不可能是( )
A.3 B.4 C.5 D.6
6.如图, , , 于点E, 于点D, , ,则 的长是( )
A.8 B.4 C.3 D.2
7.已知中,是边上的高,平分.若,,,则的度数等于( )
A. B. C. D.
8.如图,△ABC中,∠C=90°、AD是角平分线,E为AC边上的点,DE=DB,下列结论:①∠DEA+∠B=180°;② ∠CDE=∠CAB;③ AC= (AB+AE);④ S△ADC= S四边形ABDE,其中正确的结论个数为( )
A.4个 B.3个 C.2个 D.1个
9.如图,在 的网格中,每一个小正方形的边长都是1,点 , , , 都在格点上,连接 , 相交于 ,那么 的大小是( )
A. B. C. D.
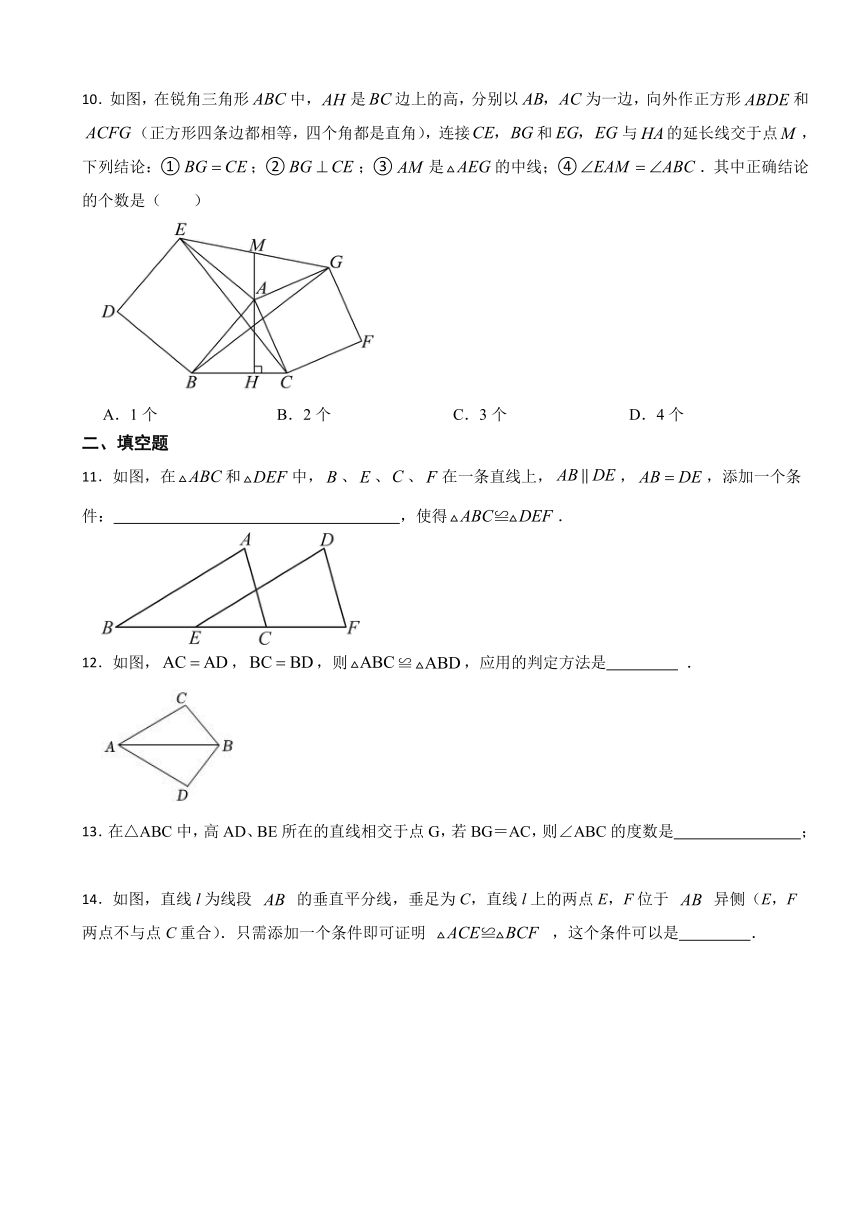
10.如图,在锐角三角形中,是边上的高,分别以为一边,向外作正方形和(正方形四条边都相等,四个角都是直角),连接和与的延长线交于点,下列结论:①;②;③是的中线;④.其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,在和中,、、、在一条直线上,,,添加一个条件: ,使得.
12.如图,,,则≌,应用的判定方法是 .
13.在△ABC中,高AD、BE所在的直线相交于点G,若BG=AC,则∠ABC的度数是 ;
14.如图,直线l为线段 的垂直平分线,垂足为C,直线l上的两点E,F位于 异侧(E,F两点不与点C重合).只需添加一个条件即可证明 ,这个条件可以是 .
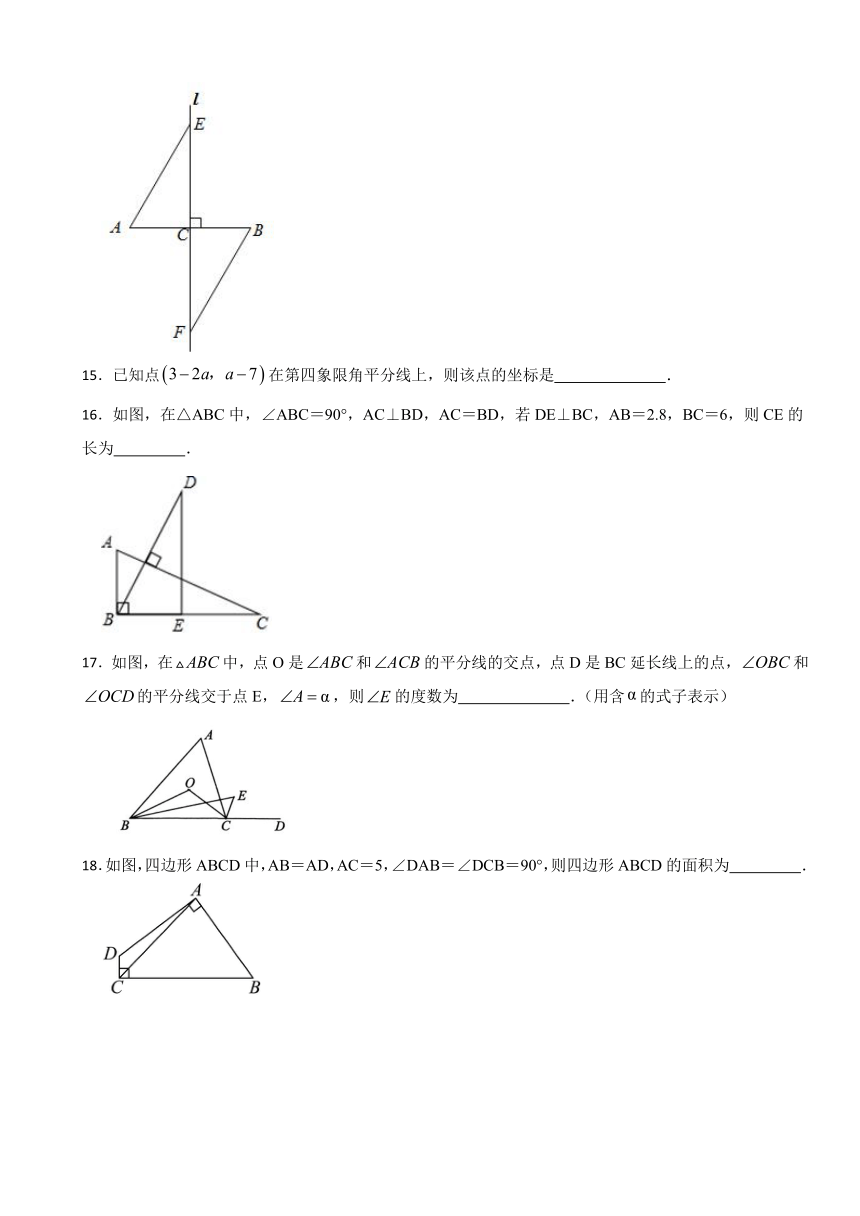
15.已知点在第四象限角平分线上,则该点的坐标是 .
16.如图,在△ABC中,∠ABC=90°,AC⊥BD,AC=BD,若DE⊥BC,AB=2.8,BC=6,则CE的长为 .
17.如图,在中,点O是和的平分线的交点,点D是BC延长线上的点,和的平分线交于点E,,则的度数为 .(用含的式子表示)
18.如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为 .
三、解答题
19.太和中学校园内有一块直角三角形(RtABC)空地,如图所示,园艺师傅以角平分线AD为界,在其两侧分别种上了不同的花草,在ABD区域内种植了月季花,在△ACD区域内种植了牡丹花,并量得两直角边AB=10m,AC=6m,分别求月季花与牡丹花两种花草的种植面积.
20.如图,已知,,,,求的度数.
21.如图,是的平分线,是的平分线.
(1)如果,,求的度数;
(2)如果,,求的度数;
22.如图①,点A,E,F,C在同一直线上,AE=CF,过点E,F分别作ED⊥AC,FB⊥AC,AB=CD.
(1)Rt△AFB≌Rt△CED;
(2)若BD与EF交于点G,试证明BD平分EF;
23.如图,已知直线与直线相交于点,.
(1)若,求的度数;
(2)若,平分,求的度数.
24.已知,点分别是上的点,点在之间,连接.
(1)如图1,若,求的度数;
(2)如图2,若点是下方一点,平分平分,已知,求的度数.
答案解析部分
1.【答案】B
2.【答案】C
3.【答案】D
4.【答案】D
5.【答案】A
6.【答案】C
7.【答案】D
8.【答案】A
9.【答案】C
10.【答案】D
11.【答案】或或
12.【答案】
13.【答案】45°或135°
14.【答案】CE=CF
15.【答案】
16.【答案】3.2
17.【答案】
18.【答案】12.5
19.【答案】,
20.【答案】
21.【答案】(1)
(2)
22.【答案】(1)解:∵AE=CF,
∴AE+EF=CF+EF,即AF=CE,
∵FB⊥AC,DE⊥AC,AB=CD
∴Rt△AFB≌Rt△CED;
(2)解:∵Rt△AFB≌Rt△CED,
∴BF=DE,
∵∠DEG=∠BGF,∠EGD=∠FGB,
∴△DEG≌△BFG,
∴EG=GF,BD平分EF.
23.【答案】(1)
(2)
24.【答案】(1)解:过点G作GH∥AB,如图所示:
∵GH∥AB,AB∥CD,
故;
(2)解:过点G作GQ∥AB,如图所示:
平分,
平分
设
由(1)可得:
∵AB∥CD,
∴∠MRC=∠BMP=72°,
.
一、单选题
1.如图,已知,,添加下列条件,能判定≌的是( )
A. B. C. D.
2.如图,已知点A与点C关于点O对称,点B与点D也关于点O对称,若,.则AB的长可能是( )
A.3 B.4 C.7 D.11
3.如图,,若,,则的度数为( )
A. B. C. D.
4.如图,中,,利用尺规在,上分别截取,,使;分别以,为圆心、以大于的长为半径作弧,两弧在内交于点;作射线交于点若的面积为,,为上一动点,则的最小值为( )
A.无法确定 B.4 C.3 D.2
5.如图,OD平分∠AOB,DE⊥AO于点E,DE=4,点F是射线OB上的任意一点,则DF的长度不可能是( )
A.3 B.4 C.5 D.6
6.如图, , , 于点E, 于点D, , ,则 的长是( )
A.8 B.4 C.3 D.2
7.已知中,是边上的高,平分.若,,,则的度数等于( )
A. B. C. D.
8.如图,△ABC中,∠C=90°、AD是角平分线,E为AC边上的点,DE=DB,下列结论:①∠DEA+∠B=180°;② ∠CDE=∠CAB;③ AC= (AB+AE);④ S△ADC= S四边形ABDE,其中正确的结论个数为( )
A.4个 B.3个 C.2个 D.1个
9.如图,在 的网格中,每一个小正方形的边长都是1,点 , , , 都在格点上,连接 , 相交于 ,那么 的大小是( )
A. B. C. D.
10.如图,在锐角三角形中,是边上的高,分别以为一边,向外作正方形和(正方形四条边都相等,四个角都是直角),连接和与的延长线交于点,下列结论:①;②;③是的中线;④.其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,在和中,、、、在一条直线上,,,添加一个条件: ,使得.
12.如图,,,则≌,应用的判定方法是 .
13.在△ABC中,高AD、BE所在的直线相交于点G,若BG=AC,则∠ABC的度数是 ;
14.如图,直线l为线段 的垂直平分线,垂足为C,直线l上的两点E,F位于 异侧(E,F两点不与点C重合).只需添加一个条件即可证明 ,这个条件可以是 .
15.已知点在第四象限角平分线上,则该点的坐标是 .
16.如图,在△ABC中,∠ABC=90°,AC⊥BD,AC=BD,若DE⊥BC,AB=2.8,BC=6,则CE的长为 .
17.如图,在中,点O是和的平分线的交点,点D是BC延长线上的点,和的平分线交于点E,,则的度数为 .(用含的式子表示)
18.如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为 .
三、解答题
19.太和中学校园内有一块直角三角形(RtABC)空地,如图所示,园艺师傅以角平分线AD为界,在其两侧分别种上了不同的花草,在ABD区域内种植了月季花,在△ACD区域内种植了牡丹花,并量得两直角边AB=10m,AC=6m,分别求月季花与牡丹花两种花草的种植面积.
20.如图,已知,,,,求的度数.
21.如图,是的平分线,是的平分线.
(1)如果,,求的度数;
(2)如果,,求的度数;
22.如图①,点A,E,F,C在同一直线上,AE=CF,过点E,F分别作ED⊥AC,FB⊥AC,AB=CD.
(1)Rt△AFB≌Rt△CED;
(2)若BD与EF交于点G,试证明BD平分EF;
23.如图,已知直线与直线相交于点,.
(1)若,求的度数;
(2)若,平分,求的度数.
24.已知,点分别是上的点,点在之间,连接.
(1)如图1,若,求的度数;
(2)如图2,若点是下方一点,平分平分,已知,求的度数.
答案解析部分
1.【答案】B
2.【答案】C
3.【答案】D
4.【答案】D
5.【答案】A
6.【答案】C
7.【答案】D
8.【答案】A
9.【答案】C
10.【答案】D
11.【答案】或或
12.【答案】
13.【答案】45°或135°
14.【答案】CE=CF
15.【答案】
16.【答案】3.2
17.【答案】
18.【答案】12.5
19.【答案】,
20.【答案】
21.【答案】(1)
(2)
22.【答案】(1)解:∵AE=CF,
∴AE+EF=CF+EF,即AF=CE,
∵FB⊥AC,DE⊥AC,AB=CD
∴Rt△AFB≌Rt△CED;
(2)解:∵Rt△AFB≌Rt△CED,
∴BF=DE,
∵∠DEG=∠BGF,∠EGD=∠FGB,
∴△DEG≌△BFG,
∴EG=GF,BD平分EF.
23.【答案】(1)
(2)
24.【答案】(1)解:过点G作GH∥AB,如图所示:
∵GH∥AB,AB∥CD,
故;
(2)解:过点G作GQ∥AB,如图所示:
平分,
平分
设
由(1)可得:
∵AB∥CD,
∴∠MRC=∠BMP=72°,
.
