物理人教版(2019)选择性必修第一册2.2简谐运动的描述(共32张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第一册2.2简谐运动的描述(共32张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 38.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-10-18 14:18:57 | ||
图片预览










文档简介
(共32张PPT)
第二章 机械振动
第2节 简谐运动的描述
高中物理选择性必修第一册
复杂机械振动
几个简谐运动
合成
分解
简谐运动是最简单、最基本的机械振动。
简谐运动与机械运动的关系是怎样的?
表达式中各字母是否有什么意义呢?
知识回顾:
简谐运动的定义:
如果物体的位移与时间的关系遵从 的规律,即它的振动图像(x-t图像)是一条 ,这样的振动是一种简谐运动。
正弦函数
正弦曲线
目标引领:
1.通过观察竖直弹簧振子的振动过程,明确振幅的定义及意义,培养从实际情境中捕捉信息,获取知识,并应用知识的能力;
2.分析拇指琴不同琴键发出不同声音的原因,通过实验探究,找到竖直弹簧振子的周期和频率的影响因素;通过观察匀速圆周运动和简谐运动的关系,寻找各种运动之间的联系,知道大自然的和谐之美,并在实验中培养科学态度和责任感;
3.通过观察两个弹簧振子的振动步调关系,理解相位及相位差的概念。
任务一:尝试一下,怎样让拇指琴发出更大的声音?
问题1:为什么拨动琴弦,就会发出声音?
怎样让琴键发出了更大的声音?
琴键发出了更大的声音时,琴键的振动有什么变化?
可见,振动幅度的大小对简谐运动来说,是一个有用的参量。
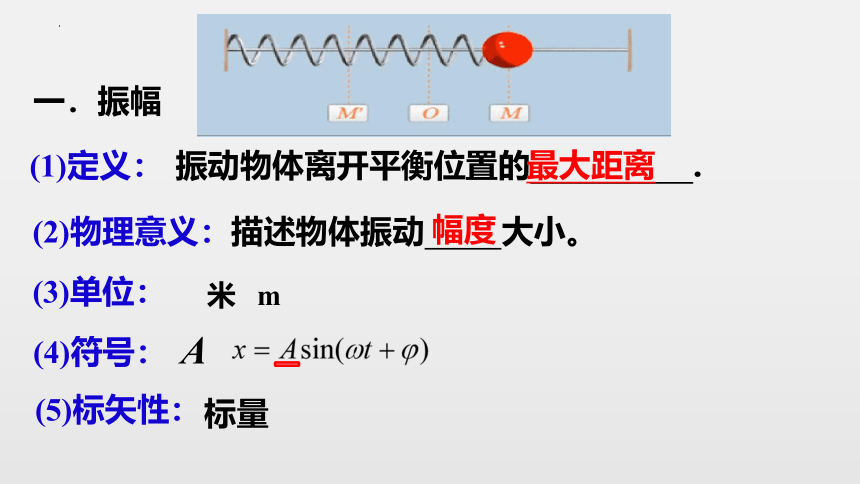
(1)定义:
振动物体离开平衡位置的 .
(3)单位:
米 m
(2)物理意义:描述物体振动 大小。
(4)符号:
A
一.振幅
幅度
最大距离
(5)标矢性:
标量
任务二:听拇指琴的声音,猜测为什么拨动不同的琴键会发出不同的声音?
可见,振动周期和频率对简谐运动来说,是一个有用的参量。
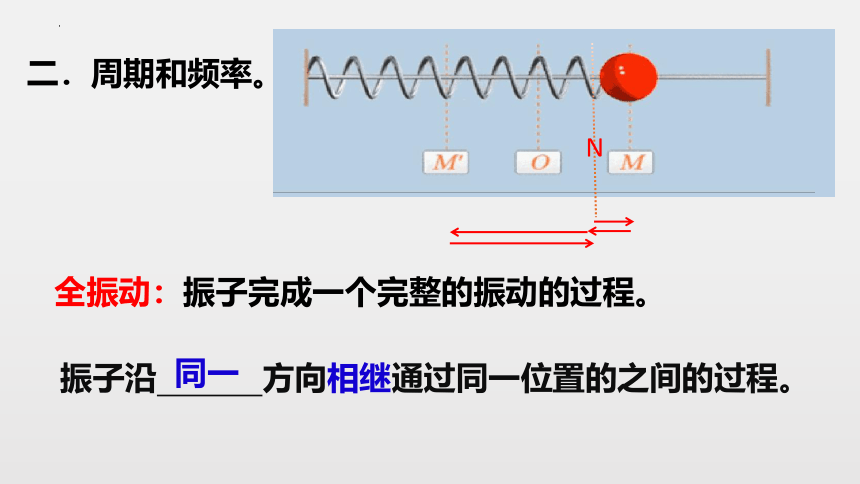
二.周期和频率。
全振动:振子完成一个完整的振动的过程。
振子沿 方向相继通过同一位置的之间的过程。
M
M/
o
同一
N
二.周期和频率。
1.周期T:
3.周期与频率的物理意义:描述物体振动的 。
(1)定义:
(2)单位:
2.频率f:
(1)定义:
(3)单位:
做简谐运动的物体完成一次全振动所需要的时间.
秒 s
物体完成的全振动的次数与所用时间的比值。
赫兹 Hz
周期越小,频率越 ,物体振动的越 。
大
快
快慢
单位
(2)数值上等于
时间内完成全振动的次数
疑问:
竖直弹簧振子的振动周期可能与哪些因素有关呢?
振幅A
振子质量m
弹簧劲度系数k
猜一猜
控制变量法
......
振幅 小振幅 中振幅 大振幅
周期
第一步实验:寻找弹簧竖直振子的振动周期与振幅的定性关系。
实验目的:①观察、对比两个弹簧竖直振子的振动周期与振幅的关系。
②利用“手机物理工坊”探究弹簧振子的周期与振幅的关系。
控制变量:同一根弹簧,同一个手机,不同的振幅
数据记录:
实验结论:
弹簧振子的周期与振幅A无关。
所有简谐运动的周期都与振幅A无关!
理论拓展:
第二步自主探究实验:探究周期与弹簧劲度系数的定性关系。
实验目的:利用“手机物理工坊”探究周期与弹簧劲度系数的关系。
控制变量:同一个手机,不同的弹簧(不再需要考虑振幅因素)
数据记录:
实验结论:
手机物理工坊
合作探究:应用手机物理传感器app寻找影响弹簧振子周期的因素。
实验注意事项:
1.振幅不用太大,否则容易出现“跳跃”;
2.尽量竖直向下拉,否则容易“荡秋千”;
3.待周期值稳定后再读数。
第二步自主探究实验:探究周期与弹簧劲度系数的定性关系。
实验目的:利用“手机物理工坊”探究周期与弹簧劲度系数的关系。
控制变量:同一个手机,不同的弹簧(不再需要考虑振幅影响)
数据记录:
实验结论:
弹簧振子的周期与劲度系数有关。
疑问:
竖直弹簧振子的振动周期可能与哪些因素有关呢?
振幅A
振子质量m
弹簧劲度系数k
猜一猜
控制变量法
......
课下探究作业:
思考:如果不借助传感器,能不能用你身边的工具测出振子的周期?怎样能尽量减小测周期时的误差?
任务:探究一下弹簧振子的周期与振子质量以及你猜测的其它因素的关系。下节课展示交流与讨论!
提示:参考课本37页的“做一做”完成!
知识回顾:
简谐运动的定义:
如果物体的位移与时间的关系遵从 的规律,即它的振动图像(x-t图像)是一条 ,这样的振动是一种简谐运动。
正弦函数
正弦曲线
表达式中有没有可以描述振动快慢的量?
知识回顾:
圆周运动中的ω叫什么名字?
与周期和频率是什么关系?
问题:
在简谐运动中ω叫什么名字?
为什么它可以描述振动的快慢?
ω与周期和频率满足什么关系?
三、圆频率ω
1.结合数学知识,推导圆频率ω与周期T、频率f的关系:
sinθ
θ
θ值每增加 ,正弦函数值完成一次循环变化.
2π
简谐运动每完成一次全振动,所需要的时间为 。
T
ωt+φ
ω(t+T)+φ
= +2π
一个匀速圆周运动的物体侧投出的影子所做的运动就是一个简谐运动。大自然中有很多的和谐之美,等着我们去发现!
2.观察实验现象,了解简谐运动与圆周运动的关系.
任务四:观察两个弹簧振子的振动,寻找两个振动步调关系。
除了振幅、周期、频率,我们还需要一个描述某个时刻物体处在哪个状态的参量!
1.相位:
2.物理意义:
3.初相:
四、相位
ωt+φ
用来描述周期性运动的物体在一个周期中的各个时刻所处的不同状态。
t=0时刻的相位 φ
【问题2】怎样用相位来描述两个弹簧振子振动的步调之间的关系?
3.相位差:
对两个具有相同频率的简谐运动
情景一:两个弹簧振子步调一致,
相位差Δφ=φ2-φ1=0,称为“同相”。
情景二:两个弹簧振子步调相反,
相位差Δφ=φ2-φ1=π,称为“反相”。
超前与滞后:
若Δφ=φ2-φ1 >0
我们称振子2的振动超前于振子1了Δφ
或者,振子1的振动滞后于振子2了Δφ
(多选)物体A做简谐运动的振动位移xA=3sin(100t+ ) m,物体B做简谐运动的振动位移xB=5sin(100t+ )m。以下说法正确的是
A.物体A的振幅是6 m,物体B的振幅是10 m
B.物体A、B的周期相等,为100 s
C.物体A振动的频率fA等于物体B振动的频率fB
D.物体A的相位超前物体B的相位
CD
目标达成检测
课下探究作业:
思考:如果不借助传感器,能不能用你身边的工具测出振子的周期?测周期的时候有什么注意事项?
任务:探究一下弹簧振子的周期与振子质量有没有关系。
提示:参考课本37页的“做一做”,独立完成!
相位差:
振幅
相位
圆频率
初相
2.观察实验现象,了解简谐运动与圆周运动的关系.
一个匀速圆周运动的物体侧投出的影子所做的运动就是一个简谐运动。大自然中有很多的和谐之美,等着我们去发现!
相位差:
振幅
相位
圆频率
初相
生活中的机械振动
数学与物理情境结合,分析初相:
φ=0
φ=
φ= -
第二章 机械振动
第2节 简谐运动的描述
高中物理选择性必修第一册
复杂机械振动
几个简谐运动
合成
分解
简谐运动是最简单、最基本的机械振动。
简谐运动与机械运动的关系是怎样的?
表达式中各字母是否有什么意义呢?
知识回顾:
简谐运动的定义:
如果物体的位移与时间的关系遵从 的规律,即它的振动图像(x-t图像)是一条 ,这样的振动是一种简谐运动。
正弦函数
正弦曲线
目标引领:
1.通过观察竖直弹簧振子的振动过程,明确振幅的定义及意义,培养从实际情境中捕捉信息,获取知识,并应用知识的能力;
2.分析拇指琴不同琴键发出不同声音的原因,通过实验探究,找到竖直弹簧振子的周期和频率的影响因素;通过观察匀速圆周运动和简谐运动的关系,寻找各种运动之间的联系,知道大自然的和谐之美,并在实验中培养科学态度和责任感;
3.通过观察两个弹簧振子的振动步调关系,理解相位及相位差的概念。
任务一:尝试一下,怎样让拇指琴发出更大的声音?
问题1:为什么拨动琴弦,就会发出声音?
怎样让琴键发出了更大的声音?
琴键发出了更大的声音时,琴键的振动有什么变化?
可见,振动幅度的大小对简谐运动来说,是一个有用的参量。
(1)定义:
振动物体离开平衡位置的 .
(3)单位:
米 m
(2)物理意义:描述物体振动 大小。
(4)符号:
A
一.振幅
幅度
最大距离
(5)标矢性:
标量
任务二:听拇指琴的声音,猜测为什么拨动不同的琴键会发出不同的声音?
可见,振动周期和频率对简谐运动来说,是一个有用的参量。
二.周期和频率。
全振动:振子完成一个完整的振动的过程。
振子沿 方向相继通过同一位置的之间的过程。
M
M/
o
同一
N
二.周期和频率。
1.周期T:
3.周期与频率的物理意义:描述物体振动的 。
(1)定义:
(2)单位:
2.频率f:
(1)定义:
(3)单位:
做简谐运动的物体完成一次全振动所需要的时间.
秒 s
物体完成的全振动的次数与所用时间的比值。
赫兹 Hz
周期越小,频率越 ,物体振动的越 。
大
快
快慢
单位
(2)数值上等于
时间内完成全振动的次数
疑问:
竖直弹簧振子的振动周期可能与哪些因素有关呢?
振幅A
振子质量m
弹簧劲度系数k
猜一猜
控制变量法
......
振幅 小振幅 中振幅 大振幅
周期
第一步实验:寻找弹簧竖直振子的振动周期与振幅的定性关系。
实验目的:①观察、对比两个弹簧竖直振子的振动周期与振幅的关系。
②利用“手机物理工坊”探究弹簧振子的周期与振幅的关系。
控制变量:同一根弹簧,同一个手机,不同的振幅
数据记录:
实验结论:
弹簧振子的周期与振幅A无关。
所有简谐运动的周期都与振幅A无关!
理论拓展:
第二步自主探究实验:探究周期与弹簧劲度系数的定性关系。
实验目的:利用“手机物理工坊”探究周期与弹簧劲度系数的关系。
控制变量:同一个手机,不同的弹簧(不再需要考虑振幅因素)
数据记录:
实验结论:
手机物理工坊
合作探究:应用手机物理传感器app寻找影响弹簧振子周期的因素。
实验注意事项:
1.振幅不用太大,否则容易出现“跳跃”;
2.尽量竖直向下拉,否则容易“荡秋千”;
3.待周期值稳定后再读数。
第二步自主探究实验:探究周期与弹簧劲度系数的定性关系。
实验目的:利用“手机物理工坊”探究周期与弹簧劲度系数的关系。
控制变量:同一个手机,不同的弹簧(不再需要考虑振幅影响)
数据记录:
实验结论:
弹簧振子的周期与劲度系数有关。
疑问:
竖直弹簧振子的振动周期可能与哪些因素有关呢?
振幅A
振子质量m
弹簧劲度系数k
猜一猜
控制变量法
......
课下探究作业:
思考:如果不借助传感器,能不能用你身边的工具测出振子的周期?怎样能尽量减小测周期时的误差?
任务:探究一下弹簧振子的周期与振子质量以及你猜测的其它因素的关系。下节课展示交流与讨论!
提示:参考课本37页的“做一做”完成!
知识回顾:
简谐运动的定义:
如果物体的位移与时间的关系遵从 的规律,即它的振动图像(x-t图像)是一条 ,这样的振动是一种简谐运动。
正弦函数
正弦曲线
表达式中有没有可以描述振动快慢的量?
知识回顾:
圆周运动中的ω叫什么名字?
与周期和频率是什么关系?
问题:
在简谐运动中ω叫什么名字?
为什么它可以描述振动的快慢?
ω与周期和频率满足什么关系?
三、圆频率ω
1.结合数学知识,推导圆频率ω与周期T、频率f的关系:
sinθ
θ
θ值每增加 ,正弦函数值完成一次循环变化.
2π
简谐运动每完成一次全振动,所需要的时间为 。
T
ωt+φ
ω(t+T)+φ
= +2π
一个匀速圆周运动的物体侧投出的影子所做的运动就是一个简谐运动。大自然中有很多的和谐之美,等着我们去发现!
2.观察实验现象,了解简谐运动与圆周运动的关系.
任务四:观察两个弹簧振子的振动,寻找两个振动步调关系。
除了振幅、周期、频率,我们还需要一个描述某个时刻物体处在哪个状态的参量!
1.相位:
2.物理意义:
3.初相:
四、相位
ωt+φ
用来描述周期性运动的物体在一个周期中的各个时刻所处的不同状态。
t=0时刻的相位 φ
【问题2】怎样用相位来描述两个弹簧振子振动的步调之间的关系?
3.相位差:
对两个具有相同频率的简谐运动
情景一:两个弹簧振子步调一致,
相位差Δφ=φ2-φ1=0,称为“同相”。
情景二:两个弹簧振子步调相反,
相位差Δφ=φ2-φ1=π,称为“反相”。
超前与滞后:
若Δφ=φ2-φ1 >0
我们称振子2的振动超前于振子1了Δφ
或者,振子1的振动滞后于振子2了Δφ
(多选)物体A做简谐运动的振动位移xA=3sin(100t+ ) m,物体B做简谐运动的振动位移xB=5sin(100t+ )m。以下说法正确的是
A.物体A的振幅是6 m,物体B的振幅是10 m
B.物体A、B的周期相等,为100 s
C.物体A振动的频率fA等于物体B振动的频率fB
D.物体A的相位超前物体B的相位
CD
目标达成检测
课下探究作业:
思考:如果不借助传感器,能不能用你身边的工具测出振子的周期?测周期的时候有什么注意事项?
任务:探究一下弹簧振子的周期与振子质量有没有关系。
提示:参考课本37页的“做一做”,独立完成!
相位差:
振幅
相位
圆频率
初相
2.观察实验现象,了解简谐运动与圆周运动的关系.
一个匀速圆周运动的物体侧投出的影子所做的运动就是一个简谐运动。大自然中有很多的和谐之美,等着我们去发现!
相位差:
振幅
相位
圆频率
初相
生活中的机械振动
数学与物理情境结合,分析初相:
φ=0
φ=
φ= -
