2.5二次函数与一元二次方程——九年级数学北师大版(2012)下册课时优化训练(含解析)
文档属性
| 名称 | 2.5二次函数与一元二次方程——九年级数学北师大版(2012)下册课时优化训练(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 528.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-19 00:08:47 | ||
图片预览



文档简介
2.5二次函数与一元二次方程
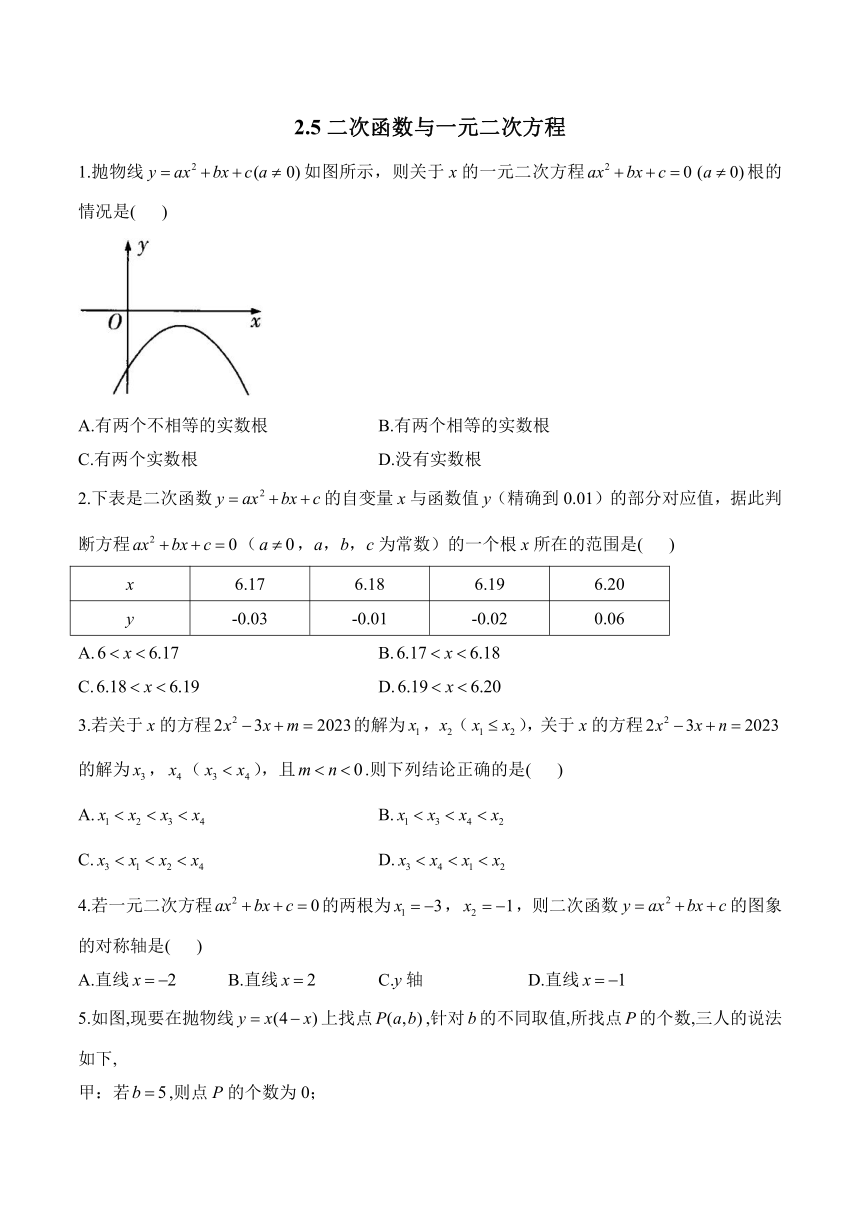
1.抛物线如图所示,则关于x的一元二次方程根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.有两个实数根 D.没有实数根
2.下表是二次函数的自变量x与函数值y(精确到0.01)的部分对应值,据此判断方程(,a,b,c为常数)的一个根x所在的范围是( )
x 6.17 6.18 6.19 6.20
y -0.03 -0.01 -0.02 0.06
A. B.
C. D.
3.若关于x的方程的解为,(),关于x的方程的解为,(),且.则下列结论正确的是( )
A. B.
C. D.
4.若一元二次方程的两根为,,则二次函数的图象的对称轴是( )
A.直线 B.直线 C.y轴 D.直线
5.如图,现要在抛物线上找点,针对b的不同取值,所找点P的个数,三人的说法如下,
甲:若,则点P的个数为0;
乙:若,则点P的个数为1;
丙:若,则点P的个数为1.
下列判断正确的是( )
A.乙错,丙对 B.甲和乙都错
C.乙对,丙错 D.甲错,丙对
6.把二次函数的图象先向上平移1个单位,再向右平移3个单位,若平移后所得抛物线与坐标轴有且只有一个交点,则m应满足条件( )
A. B. C. D.
7.已知抛物线与x轴有两个交点,,抛物线与x轴的一个交点是,则m的值是( )
A.5 B.-1 C.5或1 D.-5或-1
8.对于函数,下列说法
①图象关于y轴对称;
②有最小值;
③当方程有两个不相等的实数根时,;
④直线与函数的图象有三个交点时,正确的有个( )
A. B. C. D.
9.若函数的图象与x轴只有一个交点,则常数m的值是__________.
10.如图是二次函数的图象,对称轴为直线.若,是一元二次方程的两个根,,则的取值范围是__________.
11.如图,一次函数与二次函数的图象相交于点,,则关于x的方程的解为_________.
12.抛物线经过点、两点,则关于x的一元二次方程的解是______.
13.已知抛物线与x轴的交点为,.
(1)求一元二次方程的两个根.
(2)设抛物线与y轴交于点C,作轴交抛物线于点D,求线段CD的长.
(3)若点,在抛物线上,你能比较出p和q的大小吗?若能,请比较出大小;若不能,请说明理由.
14.已知二次函数的图象经过与两点,关于x的方程有两个根,其中一个根是3,则关于x的方程有两个整数根,求这两个整数根.
答案以及解析
1.答案:D
解析:抛物线与x轴没有交点,关于x的一元二次方程没有实数根.
2.答案:C
解析:由题表中的数据可得当时,,当时,,由此可得方程的一个根x所在的范围是.
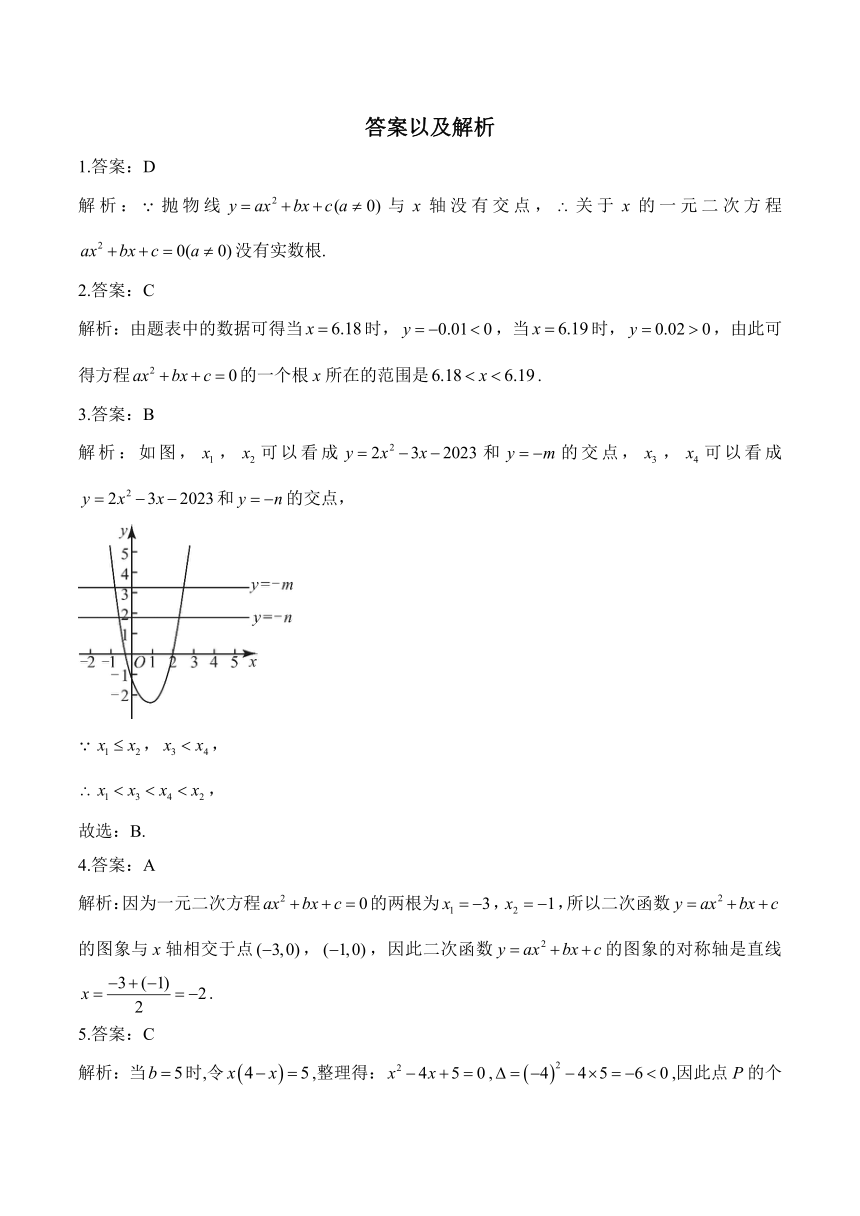
3.答案:B
解析:如图,,可以看成和的交点,,可以看成和的交点,
,,
,
故选:B.
4.答案:A
解析:因为一元二次方程的两根为,,所以二次函数的图象与x轴相交于点,,因此二次函数的图象的对称轴是直线.
5.答案:C
解析:当时,令,整理得:,,因此点P的个数为0,甲的说法正确;
当时,令,整理得:,,因此点P有1个,乙的说法正确;
当时,令,整理得:,,因此点P有2个,丙的说法不正确;
故选:C.
6.答案:C
解析:,则平移后所得抛物线的表达式为.平移后所得抛物线与坐标轴有且只有一个交点,平移后所得抛物线与x轴没有交点,,解得.
7.答案:C
解析:抛物线的对称轴为直线,抛物线的对称轴为直线,当点平移后的对应点为时,;当点平移后的对应点为时,.综上可得,m的值为5或1.
8.答案:C
解析:①当时,,
当时,,
当与时,对应的函数值相等,
图象关于y轴对称,①正确,符合题意.
②当时,,
当时,y有最小值为.
当时,,
当时,y有最小值为.
综上所述,函数有最小值为,②正确,符合题意.
③画出函数图象如图,
由图知,当或时,与两函数有两个交点,
即此时方程有两个不相等的实数根,③不正确,不符合题意.
④由题意知,有三个不相等的实数根,即有三个不相等的实数根,
设,当时,.
当时,,则函数的图象如下,
由图象知,当或时,和图象有三个交点,此时函数图象与直线图象有三个交点,④不正确,不符合题意.
故选:C.
9.答案:2或-2
解析:①当,即时,该函数是一次函数,则其图象与x轴只有一个交点;②当,即时,该函数是二次函数,则,解得.综上,m的值是2或-2.
10.答案:
解析:解法一:根据题中图象可知,原点与表示4的点到直线的距离相等,表示-1的点与表示5的点到直线的距离相等,.
解法二:已知抛物线的对称轴为直线,,.,.
11.答案:,
解析:一次函数与二次函数的图象相交于点,,关于x的方程的解为,.
12.答案:,
解析:关于x的一元二次方程
变形为
因为抛物线经过点
,
所以方程的解为,
对于方程,则或,解得或,
所以一元二方程的解为,.
故答案为,.
13.答案:(1),
(2)6
(3)能.
解析:(1)抛物线与x轴的一个交点为,
,
解得,
一元二次方程为,
解得,,
一元二次方程的两个根是,.
(2)易知抛物线的对称轴是直线,
点C到对称轴的距离是3.
轴,点C与点D关于对称轴对称,
的长是点C到对称轴距离的2倍,
即.
(3)能.
点,在抛物线上,
,
.
14.答案:或
解析:,.
方程的一个根是3,
抛物线经过点,
又抛物线经过点,,
抛物线开口向下.
如图,抛物线的对称轴为直线,
抛物线与直线的另一个交点为点,
方程的两个根为-5和3.
,,
抛物线与直线的交点的横坐标x满足或,
又方程的根为整数,或.
1.抛物线如图所示,则关于x的一元二次方程根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.有两个实数根 D.没有实数根
2.下表是二次函数的自变量x与函数值y(精确到0.01)的部分对应值,据此判断方程(,a,b,c为常数)的一个根x所在的范围是( )
x 6.17 6.18 6.19 6.20
y -0.03 -0.01 -0.02 0.06
A. B.
C. D.
3.若关于x的方程的解为,(),关于x的方程的解为,(),且.则下列结论正确的是( )
A. B.
C. D.
4.若一元二次方程的两根为,,则二次函数的图象的对称轴是( )
A.直线 B.直线 C.y轴 D.直线
5.如图,现要在抛物线上找点,针对b的不同取值,所找点P的个数,三人的说法如下,
甲:若,则点P的个数为0;
乙:若,则点P的个数为1;
丙:若,则点P的个数为1.
下列判断正确的是( )
A.乙错,丙对 B.甲和乙都错
C.乙对,丙错 D.甲错,丙对
6.把二次函数的图象先向上平移1个单位,再向右平移3个单位,若平移后所得抛物线与坐标轴有且只有一个交点,则m应满足条件( )
A. B. C. D.
7.已知抛物线与x轴有两个交点,,抛物线与x轴的一个交点是,则m的值是( )
A.5 B.-1 C.5或1 D.-5或-1
8.对于函数,下列说法
①图象关于y轴对称;
②有最小值;
③当方程有两个不相等的实数根时,;
④直线与函数的图象有三个交点时,正确的有个( )
A. B. C. D.
9.若函数的图象与x轴只有一个交点,则常数m的值是__________.
10.如图是二次函数的图象,对称轴为直线.若,是一元二次方程的两个根,,则的取值范围是__________.
11.如图,一次函数与二次函数的图象相交于点,,则关于x的方程的解为_________.
12.抛物线经过点、两点,则关于x的一元二次方程的解是______.
13.已知抛物线与x轴的交点为,.
(1)求一元二次方程的两个根.
(2)设抛物线与y轴交于点C,作轴交抛物线于点D,求线段CD的长.
(3)若点,在抛物线上,你能比较出p和q的大小吗?若能,请比较出大小;若不能,请说明理由.
14.已知二次函数的图象经过与两点,关于x的方程有两个根,其中一个根是3,则关于x的方程有两个整数根,求这两个整数根.
答案以及解析
1.答案:D
解析:抛物线与x轴没有交点,关于x的一元二次方程没有实数根.
2.答案:C
解析:由题表中的数据可得当时,,当时,,由此可得方程的一个根x所在的范围是.
3.答案:B
解析:如图,,可以看成和的交点,,可以看成和的交点,
,,
,
故选:B.
4.答案:A
解析:因为一元二次方程的两根为,,所以二次函数的图象与x轴相交于点,,因此二次函数的图象的对称轴是直线.
5.答案:C
解析:当时,令,整理得:,,因此点P的个数为0,甲的说法正确;
当时,令,整理得:,,因此点P有1个,乙的说法正确;
当时,令,整理得:,,因此点P有2个,丙的说法不正确;
故选:C.
6.答案:C
解析:,则平移后所得抛物线的表达式为.平移后所得抛物线与坐标轴有且只有一个交点,平移后所得抛物线与x轴没有交点,,解得.
7.答案:C
解析:抛物线的对称轴为直线,抛物线的对称轴为直线,当点平移后的对应点为时,;当点平移后的对应点为时,.综上可得,m的值为5或1.
8.答案:C
解析:①当时,,
当时,,
当与时,对应的函数值相等,
图象关于y轴对称,①正确,符合题意.
②当时,,
当时,y有最小值为.
当时,,
当时,y有最小值为.
综上所述,函数有最小值为,②正确,符合题意.
③画出函数图象如图,
由图知,当或时,与两函数有两个交点,
即此时方程有两个不相等的实数根,③不正确,不符合题意.
④由题意知,有三个不相等的实数根,即有三个不相等的实数根,
设,当时,.
当时,,则函数的图象如下,
由图象知,当或时,和图象有三个交点,此时函数图象与直线图象有三个交点,④不正确,不符合题意.
故选:C.
9.答案:2或-2
解析:①当,即时,该函数是一次函数,则其图象与x轴只有一个交点;②当,即时,该函数是二次函数,则,解得.综上,m的值是2或-2.
10.答案:
解析:解法一:根据题中图象可知,原点与表示4的点到直线的距离相等,表示-1的点与表示5的点到直线的距离相等,.
解法二:已知抛物线的对称轴为直线,,.,.
11.答案:,
解析:一次函数与二次函数的图象相交于点,,关于x的方程的解为,.
12.答案:,
解析:关于x的一元二次方程
变形为
因为抛物线经过点
,
所以方程的解为,
对于方程,则或,解得或,
所以一元二方程的解为,.
故答案为,.
13.答案:(1),
(2)6
(3)能.
解析:(1)抛物线与x轴的一个交点为,
,
解得,
一元二次方程为,
解得,,
一元二次方程的两个根是,.
(2)易知抛物线的对称轴是直线,
点C到对称轴的距离是3.
轴,点C与点D关于对称轴对称,
的长是点C到对称轴距离的2倍,
即.
(3)能.
点,在抛物线上,
,
.
14.答案:或
解析:,.
方程的一个根是3,
抛物线经过点,
又抛物线经过点,,
抛物线开口向下.
如图,抛物线的对称轴为直线,
抛物线与直线的另一个交点为点,
方程的两个根为-5和3.
,,
抛物线与直线的交点的横坐标x满足或,
又方程的根为整数,或.
