22.3实际问题与二次函数 教学课件(共41张PPT)初中数学人教版九年级上册
文档属性
| 名称 | 22.3实际问题与二次函数 教学课件(共41张PPT)初中数学人教版九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 25.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-19 00:00:00 | ||
图片预览






文档简介
(共41张PPT)
22.3实际问题与二次函数
第二十二章 二次函数
学习目标
分析实际问题中变量之间的二次函数关系;
能从实际问题中确定二次函数解析式及自变量的取值范围,由此确定实际问题中的最值,进而解决相关的实际问题.
问题导入
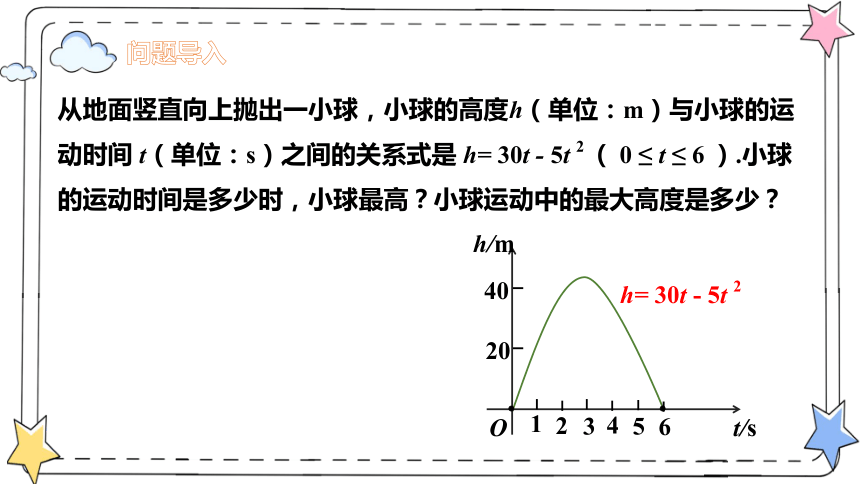
从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间 t(单位:s)之间的关系式是 h= 30t - 5t 2 ( 0 ≤ t ≤ 6 ).小球的运动时间是多少时,小球最高?小球运动中的最大高度是多少?
t/s
h/m
O
1
2
3
4
5
6
20
40
h= 30t - 5t 2
探究新知
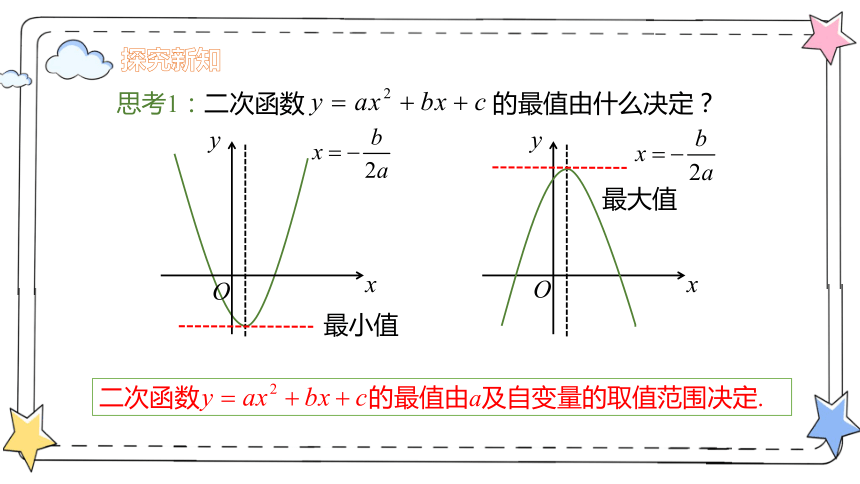
思考1:二次函数 的最值由什么决定?
x
y
O
x
y
O
最小值
最大值
二次函数 的最值由a及自变量的取值范围决定.
探究新知
思考2:当自变量 x 为全体实数时,二次函数
的最值是多少?
当a>0时,有 ,此时 .
当a<0时,有 ,此时 .
探究新知
先判断 是否在限定范围内,若在,则二次函数在 x = 时,取得最大(或小)值;若不在,则根据二次函数的增减性确定二次函数的最值.
思考3:当自变量x有限制时,二次函数 的最值如何确定?
探究新知
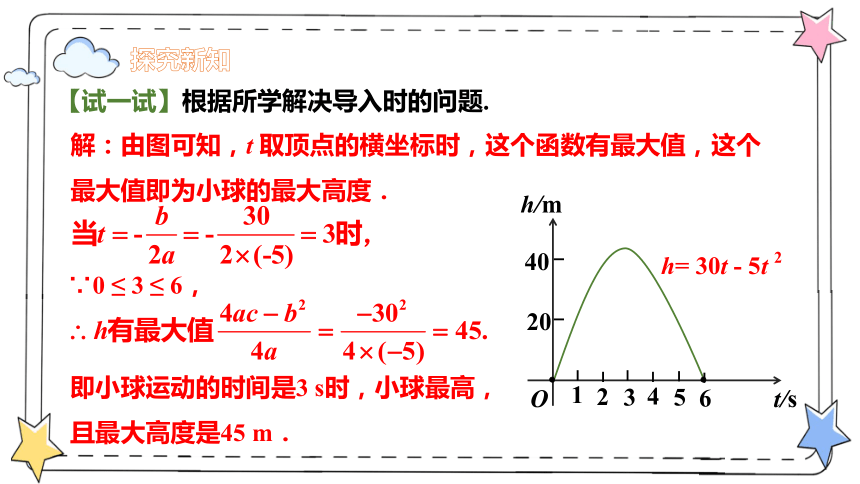
【试一试】根据所学解决导入时的问题.
t/s
h/m
O
1
2
3
4
5
6
20
40
h= 30t - 5t 2
解:由图可知,t 取顶点的横坐标时,这个函数有最大值,这个最大值即为小球的最大高度.
∵0 ≤ 3 ≤ 6,
即小球运动的时间是3 s时,小球最高,且最大高度是45 m.
可列不等式组: .
解不等式组得l的范围是 .
探究新知
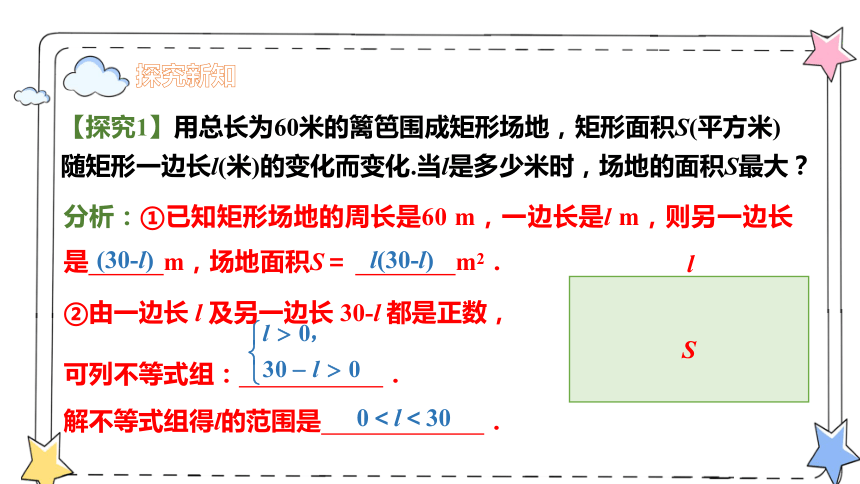
【探究1】用总长为60米的篱笆围成矩形场地,矩形面积S(平方米)随矩形一边长l(米)的变化而变化.当l是多少米时,场地的面积S最大?
l
S
0<l<30
分析:①已知矩形场地的周长是60 m,一边长是l m,则另一边长是 m,场地面积S= m2.
②由一边长 l 及另一边长 30-l 都是正数,
(30-l)
l(30-l)
探究新知
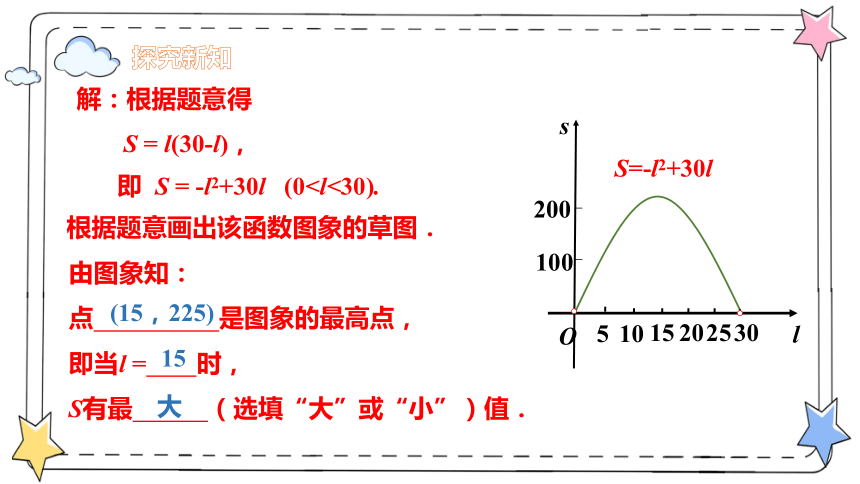
根据题意画出该函数图象的草图.
解:根据题意得
S = l(30-l),
即 S = -l2+30l (0S=-l2+30l
由图象知:
点 是图象的最高点,
即当l = 时,
S有最 (选填“大”或“小”)值.
(15,225)
15
大
5
10
15
20
25
30
100
200
l
s
O
探究新知
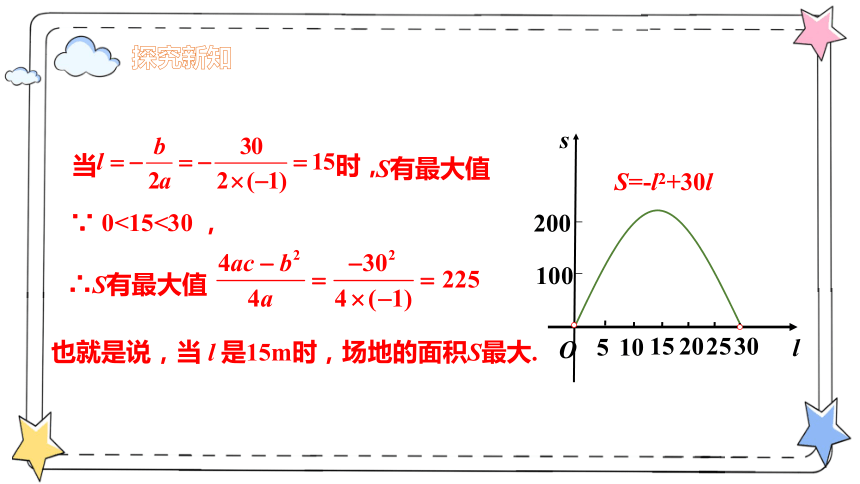
当 时,
也就是说,当 l 是15m时,场地的面积S最大.
∴S有最大值
S有最大值
∵ 0<15<30 ,
S=-l2+30l
5
10
15
20
25
30
100
200
l
s
O
探究新知
注意:实际问题中求解二次函数最值问题时,需要结合自变量的取值范围,不一定都是在顶点处取得最值.
利用二次函数解决几何图形中的最值问题的要点:
1.根据面积公式、周长公式、勾股定理等建立函数关系式;
2.确定自变量的取值范围;
3.根据开口方向、顶点坐标和自变量的取值范围画草图;
4.根据草图求所得函数在自变量的允许范围内的最大值或最小值.
随堂练习
450
随堂练习
探究新知
【探究2】某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出20件,已知商品的进价为每件40元,如何定价才能使利润最大?
数量关系
(1)销售额 = 售价×销售量;
(2)利润 = 销售额-总成本 = 单件利润×销售量;
(3)单件利润 = 售价-进价.
探究新知
调整价格包括涨价和降价两种情况.让我们一起来分析吧!
(1)涨价销售
设每件涨价x元,每星期售出商品的利润y元,填空:
单件利润(元) 销售量(件) 每星期利润(元)
正常销售
涨价销售
20
300
(20+x)
(300-10x)
(20+x)(300-10x)
6000
探究新知
(1)涨价销售
y = (60-40+x)(300-10x) = -10(x-5) 2+6 250 (0≤x≤30)
所以当 x = 5 时,y最大,也就是说在涨价的情况下,
涨价5元,即定价65元时,利润最大,最大利润是6250元
建立函数关系式:y = (20+x)(300-10x),
即:y = -10x2+100x+6 000(0≤x≤30).
探究新知
即降价2.5元时,最大利润是6125元.
建立函数关系式:
y = (60-40-x)(300+20x) = -20x2+100x+6 000 ( 0≤x≤20)
当 时,
(2)降价销售
探究新知
【问题1】根据上述结论,该如何定价才能使所获利润最大?
定价65元,所获利润最大.
【问题2】实际销售时,如果两种调价方案所获得的最大利润相差不大时,你会怎么选择?请联系实际谈一谈.
我会想尽快将商品库存清空,从而选择降价销售.
归纳总结
求解最大利润问题的一般步骤
(1)建立利润与价格之间的函数关系式:
运用“总利润 = 总售价-总成本”或“总利润 = 单件利润×销售量”
(2)结合实际意义,确定自变量的取值范围;
(3)在自变量的取值范围内确定最大利润:可以利用配方法或公式求出最大利润;也可以画出函数的简图,利用简图和性质求出.
随堂练习
某商品的进价为每件40元,已知该商品现在的售价为每件60元,每星期可卖出300件.某商场为了倾销库存,决定对该商品进行降价促销,市场调查反映:如调整价格,每降价1元,每星期可多卖出20件.那么如何定价才能使利润最大?
随堂练习
探究新知
【探究3】如图,是抛物线形拱桥,当拱顶离水面2 m时,水面宽4 m,水面下降1 m,水面宽度增加多少?
分析:我们知道,二次函数的图象是抛物线,建立适当的坐标系,就可以求出这条抛物线表示的二次函数.
为解题简便,以拋物线的顶点为原点,以抛物线的对称轴为y轴建立直角坐标系(如图).
探究新知
当水面下降1 m时,水面的纵坐标为-3.
当y = -3时, - x2 = -3,解得x1= , x2= - (舍去).
所以当水面下降1 m时,水面宽度为 m.
设这条抛物线表示的二次函数为y=ax2.
由抛物线经过点(2,-2),可得-2=a×22,a = -
这条抛物线表示的二次函数为y = - x2.
水面下降1 m,水面宽度增加 m.
探究新知
思考:还有其他建坐标系的方式吗?
注意:同一个问题中,建立平面直角坐标系的方法有多种,建立适当的平面直角坐标系能简化函数解析式,通常应使已知点在坐标轴上.
x
y
O
x
y
O
x
y
O
归纳总结
解决抛物线型实际问题的一般步骤
(1)根据题意建立适当的直角坐标系;
(2)把已知条件转化为点的坐标;
(3)合理设出函数解析式;
(4)利用待定系数法求出函数解析式;
(5)根据求得的解析式进一步分析、判断并进行有关的计算.
随堂练习
6m
随堂练习
B
D
小结
用二次函数解决实际问题的一般步骤:
1.审:仔细审题,理清题意.
2.设:找出题中的变量和常量,分析它们之间的关系,设出适当的未知数.
3.列:用二次函数表示出变量和常量之间的关系,建立二次函数模型,写出二次函数的解析式.
4.解:依据已知条件,借助二次函数的解析式、图象和性质等求解实际问题.
5.检:检验结果,进行合理取舍,得出符合实际意义的结论.
6.答:写出答案.
谢谢各位同学的观看
22.3实际问题与二次函数
第二十二章 二次函数
学习目标
分析实际问题中变量之间的二次函数关系;
能从实际问题中确定二次函数解析式及自变量的取值范围,由此确定实际问题中的最值,进而解决相关的实际问题.
问题导入
从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间 t(单位:s)之间的关系式是 h= 30t - 5t 2 ( 0 ≤ t ≤ 6 ).小球的运动时间是多少时,小球最高?小球运动中的最大高度是多少?
t/s
h/m
O
1
2
3
4
5
6
20
40
h= 30t - 5t 2
探究新知
思考1:二次函数 的最值由什么决定?
x
y
O
x
y
O
最小值
最大值
二次函数 的最值由a及自变量的取值范围决定.
探究新知
思考2:当自变量 x 为全体实数时,二次函数
的最值是多少?
当a>0时,有 ,此时 .
当a<0时,有 ,此时 .
探究新知
先判断 是否在限定范围内,若在,则二次函数在 x = 时,取得最大(或小)值;若不在,则根据二次函数的增减性确定二次函数的最值.
思考3:当自变量x有限制时,二次函数 的最值如何确定?
探究新知
【试一试】根据所学解决导入时的问题.
t/s
h/m
O
1
2
3
4
5
6
20
40
h= 30t - 5t 2
解:由图可知,t 取顶点的横坐标时,这个函数有最大值,这个最大值即为小球的最大高度.
∵0 ≤ 3 ≤ 6,
即小球运动的时间是3 s时,小球最高,且最大高度是45 m.
可列不等式组: .
解不等式组得l的范围是 .
探究新知
【探究1】用总长为60米的篱笆围成矩形场地,矩形面积S(平方米)随矩形一边长l(米)的变化而变化.当l是多少米时,场地的面积S最大?
l
S
0<l<30
分析:①已知矩形场地的周长是60 m,一边长是l m,则另一边长是 m,场地面积S= m2.
②由一边长 l 及另一边长 30-l 都是正数,
(30-l)
l(30-l)
探究新知
根据题意画出该函数图象的草图.
解:根据题意得
S = l(30-l),
即 S = -l2+30l (0
由图象知:
点 是图象的最高点,
即当l = 时,
S有最 (选填“大”或“小”)值.
(15,225)
15
大
5
10
15
20
25
30
100
200
l
s
O
探究新知
当 时,
也就是说,当 l 是15m时,场地的面积S最大.
∴S有最大值
S有最大值
∵ 0<15<30 ,
S=-l2+30l
5
10
15
20
25
30
100
200
l
s
O
探究新知
注意:实际问题中求解二次函数最值问题时,需要结合自变量的取值范围,不一定都是在顶点处取得最值.
利用二次函数解决几何图形中的最值问题的要点:
1.根据面积公式、周长公式、勾股定理等建立函数关系式;
2.确定自变量的取值范围;
3.根据开口方向、顶点坐标和自变量的取值范围画草图;
4.根据草图求所得函数在自变量的允许范围内的最大值或最小值.
随堂练习
450
随堂练习
探究新知
【探究2】某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出20件,已知商品的进价为每件40元,如何定价才能使利润最大?
数量关系
(1)销售额 = 售价×销售量;
(2)利润 = 销售额-总成本 = 单件利润×销售量;
(3)单件利润 = 售价-进价.
探究新知
调整价格包括涨价和降价两种情况.让我们一起来分析吧!
(1)涨价销售
设每件涨价x元,每星期售出商品的利润y元,填空:
单件利润(元) 销售量(件) 每星期利润(元)
正常销售
涨价销售
20
300
(20+x)
(300-10x)
(20+x)(300-10x)
6000
探究新知
(1)涨价销售
y = (60-40+x)(300-10x) = -10(x-5) 2+6 250 (0≤x≤30)
所以当 x = 5 时,y最大,也就是说在涨价的情况下,
涨价5元,即定价65元时,利润最大,最大利润是6250元
建立函数关系式:y = (20+x)(300-10x),
即:y = -10x2+100x+6 000(0≤x≤30).
探究新知
即降价2.5元时,最大利润是6125元.
建立函数关系式:
y = (60-40-x)(300+20x) = -20x2+100x+6 000 ( 0≤x≤20)
当 时,
(2)降价销售
探究新知
【问题1】根据上述结论,该如何定价才能使所获利润最大?
定价65元,所获利润最大.
【问题2】实际销售时,如果两种调价方案所获得的最大利润相差不大时,你会怎么选择?请联系实际谈一谈.
我会想尽快将商品库存清空,从而选择降价销售.
归纳总结
求解最大利润问题的一般步骤
(1)建立利润与价格之间的函数关系式:
运用“总利润 = 总售价-总成本”或“总利润 = 单件利润×销售量”
(2)结合实际意义,确定自变量的取值范围;
(3)在自变量的取值范围内确定最大利润:可以利用配方法或公式求出最大利润;也可以画出函数的简图,利用简图和性质求出.
随堂练习
某商品的进价为每件40元,已知该商品现在的售价为每件60元,每星期可卖出300件.某商场为了倾销库存,决定对该商品进行降价促销,市场调查反映:如调整价格,每降价1元,每星期可多卖出20件.那么如何定价才能使利润最大?
随堂练习
探究新知
【探究3】如图,是抛物线形拱桥,当拱顶离水面2 m时,水面宽4 m,水面下降1 m,水面宽度增加多少?
分析:我们知道,二次函数的图象是抛物线,建立适当的坐标系,就可以求出这条抛物线表示的二次函数.
为解题简便,以拋物线的顶点为原点,以抛物线的对称轴为y轴建立直角坐标系(如图).
探究新知
当水面下降1 m时,水面的纵坐标为-3.
当y = -3时, - x2 = -3,解得x1= , x2= - (舍去).
所以当水面下降1 m时,水面宽度为 m.
设这条抛物线表示的二次函数为y=ax2.
由抛物线经过点(2,-2),可得-2=a×22,a = -
这条抛物线表示的二次函数为y = - x2.
水面下降1 m,水面宽度增加 m.
探究新知
思考:还有其他建坐标系的方式吗?
注意:同一个问题中,建立平面直角坐标系的方法有多种,建立适当的平面直角坐标系能简化函数解析式,通常应使已知点在坐标轴上.
x
y
O
x
y
O
x
y
O
归纳总结
解决抛物线型实际问题的一般步骤
(1)根据题意建立适当的直角坐标系;
(2)把已知条件转化为点的坐标;
(3)合理设出函数解析式;
(4)利用待定系数法求出函数解析式;
(5)根据求得的解析式进一步分析、判断并进行有关的计算.
随堂练习
6m
随堂练习
B
D
小结
用二次函数解决实际问题的一般步骤:
1.审:仔细审题,理清题意.
2.设:找出题中的变量和常量,分析它们之间的关系,设出适当的未知数.
3.列:用二次函数表示出变量和常量之间的关系,建立二次函数模型,写出二次函数的解析式.
4.解:依据已知条件,借助二次函数的解析式、图象和性质等求解实际问题.
5.检:检验结果,进行合理取舍,得出符合实际意义的结论.
6.答:写出答案.
谢谢各位同学的观看
同课章节目录
