23.2.3关于原点对称的点的坐标 教学课件(共25张PPT)初中数学人教版九年级上册
文档属性
| 名称 | 23.2.3关于原点对称的点的坐标 教学课件(共25张PPT)初中数学人教版九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 24.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-19 12:31:31 | ||
图片预览






文档简介
(共25张PPT)
23.2.3关于原点对称的点的坐标
第二十三章 旋转
学习目标
掌握两点关于原点对称时,横纵坐标的关系;
能够在平面直角坐标系内作关于原点对称的图形.
知识回顾
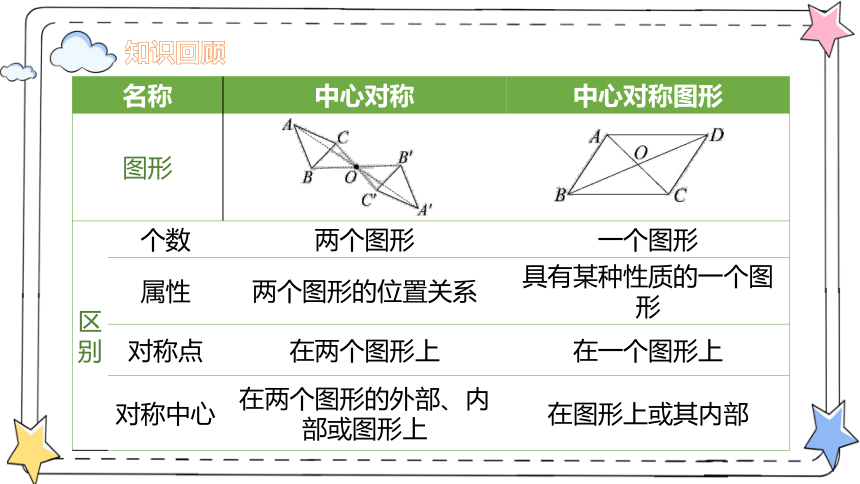
名称 中心对称 中心对称图形
图形
区别 个数 两个图形 一个图形
属性 两个图形的位置关系 具有某种性质的一个图形
对称点 在两个图形上 在一个图形上
对称中心 在两个图形的外部、内部或图形上 在图形上或其内部
复习导入
(1)你能说出点P关于x轴对称点的坐标吗?
A(x,-y)
P(x,y)
关于x轴对称
在平面坐标系中,关于x轴对称的点的横坐标相等,纵坐标互为相反数.
P(-3,2)
A(-3,- 2 )
1
2
3
4
5
-4
-3
-2
-1
·
O
x
3
1
4
2
5
-2
-4
-1
-3
y
复习导入
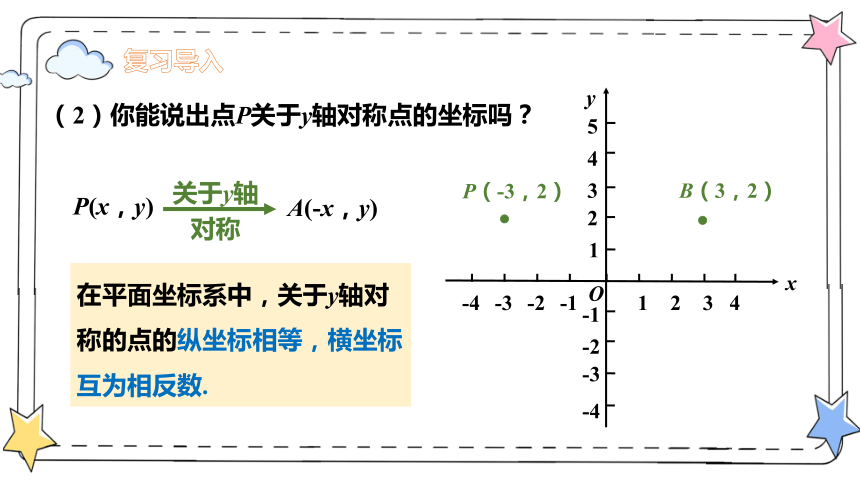
(2)你能说出点P关于y轴对称点的坐标吗?
A(-x,y)
P(x,y)
关于y轴对称
在平面坐标系中,关于y轴对称的点的纵坐标相等,横坐标互为相反数.
B(3,2)
P(-3,2)
1
2
3
-4
-3
-2
-1
O
x
3
1
4
2
5
-2
-4
-1
-3
y
4
复习导入
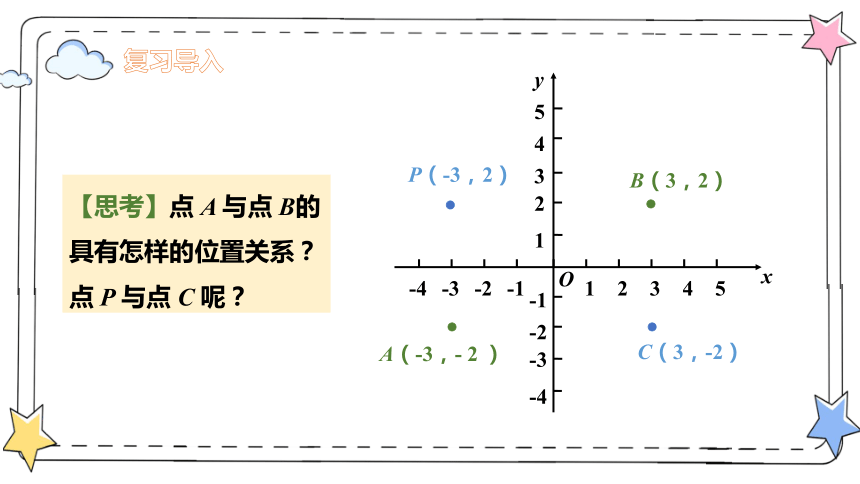
【思考】点 A 与点 B的具有怎样的位置关系?点 P 与点 C 呢?
1
2
3
4
5
-4
-3
-2
-1
O
x
3
1
4
2
5
-2
-4
-1
-3
y
C(3,-2)
A(-3,- 2 )
B(3,2)
P(-3,2)
探究新知
如图,在直角坐标系中,作出下列已知点关于原点O的对称点,并写出它们的坐标.
A(4,0),B(0,-3),C(2,1),D(-1,2),E(-3,-4).
A′( -4,0 ) ,B′ ( 0,3 ),C′ ( -2,-1 ) ,
D′ ( 1, -2 ) ,E′ ( 3,4 ).
1
2
3
4
-4
-3
-2
-1
x
y
1
2
3
4
-4
-3
-2
-1
O
E
B
C
A
D
A'
B'
C'
D'
E'
探究新知
A(4,0)
B(0,-3)
C(2,1)
D(-1,2)
E(-3,-4)
A'(-4,0)
B'(0,-3)
C'(-2,-1)
D'(1,-2)
E'(3,4)
观察表格,在直角坐标系中,关于原点对称的两个点的坐标之间有什么关系?
横坐标、纵坐标都互为相反数.
P′(-x,-y)
P(x,y)
关于原点对称
归纳总结
关于坐标轴、原点对称的点的坐标特征
对称情况 坐标间的关系 表示
关于坐标轴对称
关于原点对称
关于x轴对称
关于y轴对称
横坐标相同,纵坐标互为相反数
横坐标互为相反数,纵坐标相同
P(a,b)关于x轴的对称点为P1(a,-b)
P(a,b)关于y轴的对称点为P2(-a,b)
横、纵坐标都互为相反数
P(a,b)关于原点的对称点为P3(-a,-b)
例题练习
如图,利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称的图形.
3
1
4
2
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
y
A
C
B
x
P′(-x,-y)
P(x,y)
关于原点对称
例题练习
解:△ABC 的三个顶点
A(-4,1),B( -1,-1),C( -3,2 )
关于原点的对称点分别为
A′(4,-1),B′(1,1),C′(3,-2)
依次连接A′B′,B′C′,C′A′,
就可得到与 △ABC 关于原点对称的△A′B′C′.
3
1
4
2
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
y
A
C
B
x
A′
C′
B′
归纳总结
作关于原点对称的图形的步骤:
1. 找出给定图形上具有代表性的点;
2. 写出这些点关于原点对称的点的坐标;
3. 在平面直角坐标系中描出这些对称点;
4. 顺次连接对称点,即为所求作的对称图形.
B
B
D
C
-8
8
小结
对称情况 坐标间的关系 表示
关于x轴对称
关于y轴对称
关于原点对称
横坐标相同,纵坐标互为相反数
横坐标互为相反数,纵坐标相同
P(a,b)关于x轴的对称点为P1(a,-b)
P(a,b)关于y轴的对称点为P2(-a,b)
横、纵坐标都互为相反数
P(a,b)关于原点的对称点为P3(-a,-b)
谢谢各位同学的观看
23.2.3关于原点对称的点的坐标
第二十三章 旋转
学习目标
掌握两点关于原点对称时,横纵坐标的关系;
能够在平面直角坐标系内作关于原点对称的图形.
知识回顾
名称 中心对称 中心对称图形
图形
区别 个数 两个图形 一个图形
属性 两个图形的位置关系 具有某种性质的一个图形
对称点 在两个图形上 在一个图形上
对称中心 在两个图形的外部、内部或图形上 在图形上或其内部
复习导入
(1)你能说出点P关于x轴对称点的坐标吗?
A(x,-y)
P(x,y)
关于x轴对称
在平面坐标系中,关于x轴对称的点的横坐标相等,纵坐标互为相反数.
P(-3,2)
A(-3,- 2 )
1
2
3
4
5
-4
-3
-2
-1
·
O
x
3
1
4
2
5
-2
-4
-1
-3
y
复习导入
(2)你能说出点P关于y轴对称点的坐标吗?
A(-x,y)
P(x,y)
关于y轴对称
在平面坐标系中,关于y轴对称的点的纵坐标相等,横坐标互为相反数.
B(3,2)
P(-3,2)
1
2
3
-4
-3
-2
-1
O
x
3
1
4
2
5
-2
-4
-1
-3
y
4
复习导入
【思考】点 A 与点 B的具有怎样的位置关系?点 P 与点 C 呢?
1
2
3
4
5
-4
-3
-2
-1
O
x
3
1
4
2
5
-2
-4
-1
-3
y
C(3,-2)
A(-3,- 2 )
B(3,2)
P(-3,2)
探究新知
如图,在直角坐标系中,作出下列已知点关于原点O的对称点,并写出它们的坐标.
A(4,0),B(0,-3),C(2,1),D(-1,2),E(-3,-4).
A′( -4,0 ) ,B′ ( 0,3 ),C′ ( -2,-1 ) ,
D′ ( 1, -2 ) ,E′ ( 3,4 ).
1
2
3
4
-4
-3
-2
-1
x
y
1
2
3
4
-4
-3
-2
-1
O
E
B
C
A
D
A'
B'
C'
D'
E'
探究新知
A(4,0)
B(0,-3)
C(2,1)
D(-1,2)
E(-3,-4)
A'(-4,0)
B'(0,-3)
C'(-2,-1)
D'(1,-2)
E'(3,4)
观察表格,在直角坐标系中,关于原点对称的两个点的坐标之间有什么关系?
横坐标、纵坐标都互为相反数.
P′(-x,-y)
P(x,y)
关于原点对称
归纳总结
关于坐标轴、原点对称的点的坐标特征
对称情况 坐标间的关系 表示
关于坐标轴对称
关于原点对称
关于x轴对称
关于y轴对称
横坐标相同,纵坐标互为相反数
横坐标互为相反数,纵坐标相同
P(a,b)关于x轴的对称点为P1(a,-b)
P(a,b)关于y轴的对称点为P2(-a,b)
横、纵坐标都互为相反数
P(a,b)关于原点的对称点为P3(-a,-b)
例题练习
如图,利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称的图形.
3
1
4
2
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
y
A
C
B
x
P′(-x,-y)
P(x,y)
关于原点对称
例题练习
解:△ABC 的三个顶点
A(-4,1),B( -1,-1),C( -3,2 )
关于原点的对称点分别为
A′(4,-1),B′(1,1),C′(3,-2)
依次连接A′B′,B′C′,C′A′,
就可得到与 △ABC 关于原点对称的△A′B′C′.
3
1
4
2
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
y
A
C
B
x
A′
C′
B′
归纳总结
作关于原点对称的图形的步骤:
1. 找出给定图形上具有代表性的点;
2. 写出这些点关于原点对称的点的坐标;
3. 在平面直角坐标系中描出这些对称点;
4. 顺次连接对称点,即为所求作的对称图形.
B
B
D
C
-8
8
小结
对称情况 坐标间的关系 表示
关于x轴对称
关于y轴对称
关于原点对称
横坐标相同,纵坐标互为相反数
横坐标互为相反数,纵坐标相同
P(a,b)关于x轴的对称点为P1(a,-b)
P(a,b)关于y轴的对称点为P2(-a,b)
横、纵坐标都互为相反数
P(a,b)关于原点的对称点为P3(-a,-b)
谢谢各位同学的观看
同课章节目录
