6.3 平面向量线性运算的应用 课件(共37张PPT)——高中数学人教B版(2019)必修第二册
文档属性
| 名称 | 6.3 平面向量线性运算的应用 课件(共37张PPT)——高中数学人教B版(2019)必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 37.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-18 18:46:51 | ||
图片预览











文档简介
(共37张PPT)
人教B版(2019)必修第二册
6.3平面向量线性运算的应用
学习目标
Learning Objectives
探索新知
Explore new knowledge
题型突破
Breakthrough in question types
当堂检测
Classroom test
学习目录
parent conference directory
壹
叁
贰
肆
学习目标
part 01
学习目标
01
会用向量法计算或证明平面几何中的相关问题
01
会用向量法解决某些简单的物理学中的问题
02
探索新知
part 02
探索新知
02
概念讲解
知识点1 向量在平面几何中的应用
在学习向量及其运算时,我们已经看到向量在三角形、平行四边形等平面几何中的应用.实际上,利用平面向量可以很好地描述有关全等、相似平行等关系,从而可以求解和证明平面几何问题.
探索新知
02
例1 如图所示,MN 是△ABC 的中位线求证:MN // BC 且 MN BC.
解:因为 M,N 分别是 AB,AC 的中点,
所以 ,,
因此 ,
A
B
C
M
N
所以 MN // BC,且 MN = BC.
例1的结论是大家非常熟悉的三角形中位线定理,初中的时候我们是利用平行四边形的性质来证明的,但这里只用到了平面向量的线性运算.
探索新知
02
例2 如图所示,已知平行四边形 ABCD 中,E、F 在对角线 BD 上,并且 BE = FD. 求证:四边形 AECF 是平行四边形.
解:由已知可设:,,
则 ,,
又因为 ,所以 ,
E
F
A
B
C
D
因此 AE 平行且相等于 FC,所以四边形 AECF 是平行四边形.
例2用初中的三角形全等也能证明,但是我们这里还只是只用到了平面向量的线性运算.
探索新知
02
尝试与发现
思考:结合上述两个例题,说说用向量法解决平面几何问题的基本思路是什么?
先用向量表示相应的点、线段、夹角等几何元素,然后通过向量的运算来研究点、线段等元素之间的关系,最后再把运算结果“翻译”成几何关系,便得到几何问题的结论.
知识点1 向量在平面几何中的应用
探索新知
02
归纳小结
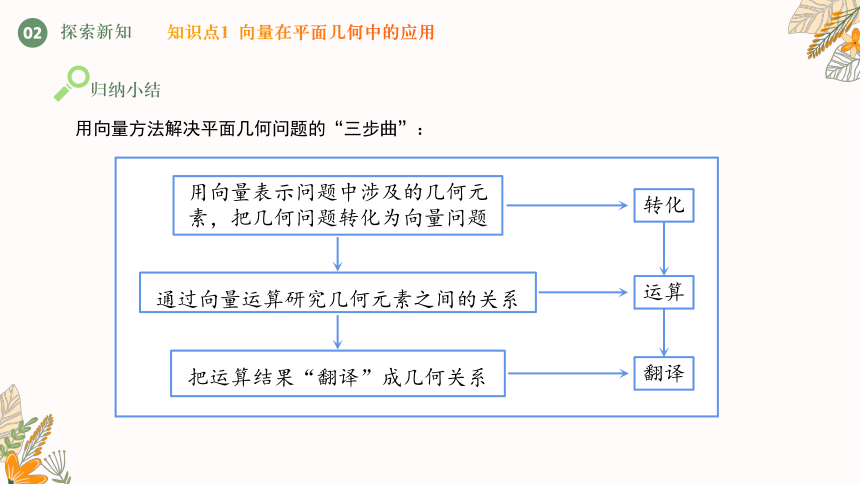
用向量方法解决平面几何问题的“三步曲”:
知识点1 向量在平面几何中的应用
用向量表示问题中涉及的几何元素,把几何问题转化为向量问题
通过向量运算研究几何元素之间的关系
把运算结果“翻译”成几何关系
转化
翻译
运算
探索新知
02
例3 如图所示,已知 △ABC 中,E,F 分别 AB,BC 的中点,AF 与 CE 相交于点 O,求 AO : OF 与 CO : OE 的值.
解:因为 = ,又因为E、F都是中点,
所以 .
B
A
C
F
E
O
另外 ,所以 ;
设,,则有,
即,由共线定理可知 s t 2;
因此 AO : OF CO : OE 2 : 1 .
例3中的O点是△ABC的重心.同样,我们这里是利用平面向量的线性运算得到了三角形重心的一个性质,这个性质如果用相似三角形等知识来证明,需要添加辅助线.
探索新知
02
总结与归纳
平面向量在平面几何中的应用主要是用向量的线性运算解决平面几何中的平行、长度等问题.
(1)证明线段平行或点共线问题,包括相似问题,常用共线向量基本定理:
.
知识点1 向量在平面几何中的应用
如果a≠0且b∥a,则存在唯一的实数λ,使得b=λa
(2)求线段的长度或说明线段相等,可以用向量的模:若a=(x,y),则
(3)对于有些平面几何(如长方形、正方形、直角三角形等)问题,常用向量的坐标法,建立平面直角坐标系,把向量用坐标表示出来,通过代数运算来解决.
探索新知
02
尝试与发现
我们在物理中已经学习过,利用向量可以描述物理学中的位移、力、速度、加速度等,因此,在涉及这些量的运算时,我们都可以借助向量来完成.
例如,从物理学中我们知道,同一个力F可以分解成无数对大小、方向不同的分力.从数学上来说,这是因为对于同一条对角线,可以有无数个平行四边形,如图所示.
知识点2 向量在物理中的应用
F
探索新知
02
尝试与发现
又如,如果一个质点O处于平衡状态,而且受到多个力的作用,那就是说这些力的合力为零.特别地,如果两个力 F1,F2 的合力为零,则 F1 + F2 = 0,即这两个力互为相反向量,如图(1)所示;
知识点2 向量在物理中的作用
O
F1
F2
(1)
如果三个力 F1,F2,F2 的合力为零,则 F1 + F2 + F3 = 0,
即其中任意两个力的合力是另一个力的相反向量,如图(2)所示.
O
F1
F2
F1 + F2
F3
(2)
探索新知
02
例4 如图所示,一个物体被两根轻质细绳拉住,且处于平衡状态,已知物体所受的重力大小为 50 N,求每条绳上的拉力大小.
解:因为物体处于平衡状态,所以 是重力的相反向量,
因此 || = 50 N.
又根据向量加法的平行四边形法则可知,的方向是竖直向上的,
F1
F2
45°
45°
且 ,
所以 ;
因此每条绳上的拉力为 N.
探索新知
02
例5 如图所示,把一个物体放在倾角为的斜面上,物体处于平衡状态,且受到三个力的作用,即重力 G,沿着斜面向上的摩擦力 F1,垂直斜面向上的弹力 F2 ,已知 |G| = 100 N,求 F1,F2 大小.
解:建立如图示的平面直角坐标系,则
又由已知可得
F1
F2
30°
G
(1)
F1
x
y
30°
G
F2
(2)
且,所以
从而可知,
题型突破
part 03
题型突破
03
题型1 利用向量解决平面几何中的平行问题
例1. 如图,已知AC,BD是梯形ABCD的对角线,E,F分别是BD,AC的中点,求证:EF∥BC.
题型突破
03
题型1 利用向量解决平面几何中的平行问题
连接BF.
∵F是AC的中点,
题型突破
03
题型1 利用向量解决平面几何中的平行问题
试用坐标法证明本例题.
证明: 如图,建立平面直角坐标系.
题型突破
03
解题通法
平面几何中证明两直线平行问题,可转化为证明向量共线问题,
即寻找一个实数λ,使得一个向量可以用另一个向量与λ的乘积表示,
也可以通过坐标运算进行.
题型1 利用向量解决平面几何中的平行问题
题型突破
03
题型2 向量基底法在平面几何中的应用
例2. 如图,点O是平行四边形ABCD的对角线的交点,E,F分别在边CD,AB上,且
题型突破
03
题型2 向量基底法在平面几何中的应用
题型突破
03
题型3 向量在物理学中的应用
例3. 在风速为75(-) km/h的西风中,飞机以150 km/h的航速向西北方向飞行,求没有风时飞机的航速和航向.
设w=风速,va=有风时飞机的航行速度,vb=无风时飞机的航行速度,vb=va-w.如右图所示.
∴vb,va,w构成三角形.设||=|va|,||=|w|,||=|vb|,
作AD∥BC,CD⊥AD于点D,BE⊥AD于点E,则∠BAD=45°.
设||=150,则||=75(-).
∴||=||=||=75,||=75.
从而||=150,∠CAD=30°.
∴|vb|=150km/h,方向为北偏西60°.
题型突破
03
例4. 如图,物体W的质量为50 kg,用绳子将物体W悬挂在两面墙之间,已知两面墙之间的距离AB=10 m(AB为水平线),AC=6 m,BC=8 m,求AC,BC上所受的力的大小(g取9.8 m/s2).
题型3 向量在物理学中的应用
题型突破
03
题型3 向量在物理学中的应用
题型突破
03
解题通法
用向量方法解决物理问题的步骤
(1)把物理问题中的相关量用向量表示.
(2)转化为向量问题的模型,通过向量运算使问题解决.
(3)结果还原为物理问题.
题型3 向量在物理学中的应用
当堂检测
part 04
当堂检测
04
当堂检测
04
ABC
当堂检测
04
当堂检测
04
当堂检测
04
当堂检测
04
当堂检测
04
当堂检测
04
老师名字
谢谢观看
learn to report
人教B版(2019)必修第二册
6.3平面向量线性运算的应用
学习目标
Learning Objectives
探索新知
Explore new knowledge
题型突破
Breakthrough in question types
当堂检测
Classroom test
学习目录
parent conference directory
壹
叁
贰
肆
学习目标
part 01
学习目标
01
会用向量法计算或证明平面几何中的相关问题
01
会用向量法解决某些简单的物理学中的问题
02
探索新知
part 02
探索新知
02
概念讲解
知识点1 向量在平面几何中的应用
在学习向量及其运算时,我们已经看到向量在三角形、平行四边形等平面几何中的应用.实际上,利用平面向量可以很好地描述有关全等、相似平行等关系,从而可以求解和证明平面几何问题.
探索新知
02
例1 如图所示,MN 是△ABC 的中位线求证:MN // BC 且 MN BC.
解:因为 M,N 分别是 AB,AC 的中点,
所以 ,,
因此 ,
A
B
C
M
N
所以 MN // BC,且 MN = BC.
例1的结论是大家非常熟悉的三角形中位线定理,初中的时候我们是利用平行四边形的性质来证明的,但这里只用到了平面向量的线性运算.
探索新知
02
例2 如图所示,已知平行四边形 ABCD 中,E、F 在对角线 BD 上,并且 BE = FD. 求证:四边形 AECF 是平行四边形.
解:由已知可设:,,
则 ,,
又因为 ,所以 ,
E
F
A
B
C
D
因此 AE 平行且相等于 FC,所以四边形 AECF 是平行四边形.
例2用初中的三角形全等也能证明,但是我们这里还只是只用到了平面向量的线性运算.
探索新知
02
尝试与发现
思考:结合上述两个例题,说说用向量法解决平面几何问题的基本思路是什么?
先用向量表示相应的点、线段、夹角等几何元素,然后通过向量的运算来研究点、线段等元素之间的关系,最后再把运算结果“翻译”成几何关系,便得到几何问题的结论.
知识点1 向量在平面几何中的应用
探索新知
02
归纳小结
用向量方法解决平面几何问题的“三步曲”:
知识点1 向量在平面几何中的应用
用向量表示问题中涉及的几何元素,把几何问题转化为向量问题
通过向量运算研究几何元素之间的关系
把运算结果“翻译”成几何关系
转化
翻译
运算
探索新知
02
例3 如图所示,已知 △ABC 中,E,F 分别 AB,BC 的中点,AF 与 CE 相交于点 O,求 AO : OF 与 CO : OE 的值.
解:因为 = ,又因为E、F都是中点,
所以 .
B
A
C
F
E
O
另外 ,所以 ;
设,,则有,
即,由共线定理可知 s t 2;
因此 AO : OF CO : OE 2 : 1 .
例3中的O点是△ABC的重心.同样,我们这里是利用平面向量的线性运算得到了三角形重心的一个性质,这个性质如果用相似三角形等知识来证明,需要添加辅助线.
探索新知
02
总结与归纳
平面向量在平面几何中的应用主要是用向量的线性运算解决平面几何中的平行、长度等问题.
(1)证明线段平行或点共线问题,包括相似问题,常用共线向量基本定理:
.
知识点1 向量在平面几何中的应用
如果a≠0且b∥a,则存在唯一的实数λ,使得b=λa
(2)求线段的长度或说明线段相等,可以用向量的模:若a=(x,y),则
(3)对于有些平面几何(如长方形、正方形、直角三角形等)问题,常用向量的坐标法,建立平面直角坐标系,把向量用坐标表示出来,通过代数运算来解决.
探索新知
02
尝试与发现
我们在物理中已经学习过,利用向量可以描述物理学中的位移、力、速度、加速度等,因此,在涉及这些量的运算时,我们都可以借助向量来完成.
例如,从物理学中我们知道,同一个力F可以分解成无数对大小、方向不同的分力.从数学上来说,这是因为对于同一条对角线,可以有无数个平行四边形,如图所示.
知识点2 向量在物理中的应用
F
探索新知
02
尝试与发现
又如,如果一个质点O处于平衡状态,而且受到多个力的作用,那就是说这些力的合力为零.特别地,如果两个力 F1,F2 的合力为零,则 F1 + F2 = 0,即这两个力互为相反向量,如图(1)所示;
知识点2 向量在物理中的作用
O
F1
F2
(1)
如果三个力 F1,F2,F2 的合力为零,则 F1 + F2 + F3 = 0,
即其中任意两个力的合力是另一个力的相反向量,如图(2)所示.
O
F1
F2
F1 + F2
F3
(2)
探索新知
02
例4 如图所示,一个物体被两根轻质细绳拉住,且处于平衡状态,已知物体所受的重力大小为 50 N,求每条绳上的拉力大小.
解:因为物体处于平衡状态,所以 是重力的相反向量,
因此 || = 50 N.
又根据向量加法的平行四边形法则可知,的方向是竖直向上的,
F1
F2
45°
45°
且 ,
所以 ;
因此每条绳上的拉力为 N.
探索新知
02
例5 如图所示,把一个物体放在倾角为的斜面上,物体处于平衡状态,且受到三个力的作用,即重力 G,沿着斜面向上的摩擦力 F1,垂直斜面向上的弹力 F2 ,已知 |G| = 100 N,求 F1,F2 大小.
解:建立如图示的平面直角坐标系,则
又由已知可得
F1
F2
30°
G
(1)
F1
x
y
30°
G
F2
(2)
且,所以
从而可知,
题型突破
part 03
题型突破
03
题型1 利用向量解决平面几何中的平行问题
例1. 如图,已知AC,BD是梯形ABCD的对角线,E,F分别是BD,AC的中点,求证:EF∥BC.
题型突破
03
题型1 利用向量解决平面几何中的平行问题
连接BF.
∵F是AC的中点,
题型突破
03
题型1 利用向量解决平面几何中的平行问题
试用坐标法证明本例题.
证明: 如图,建立平面直角坐标系.
题型突破
03
解题通法
平面几何中证明两直线平行问题,可转化为证明向量共线问题,
即寻找一个实数λ,使得一个向量可以用另一个向量与λ的乘积表示,
也可以通过坐标运算进行.
题型1 利用向量解决平面几何中的平行问题
题型突破
03
题型2 向量基底法在平面几何中的应用
例2. 如图,点O是平行四边形ABCD的对角线的交点,E,F分别在边CD,AB上,且
题型突破
03
题型2 向量基底法在平面几何中的应用
题型突破
03
题型3 向量在物理学中的应用
例3. 在风速为75(-) km/h的西风中,飞机以150 km/h的航速向西北方向飞行,求没有风时飞机的航速和航向.
设w=风速,va=有风时飞机的航行速度,vb=无风时飞机的航行速度,vb=va-w.如右图所示.
∴vb,va,w构成三角形.设||=|va|,||=|w|,||=|vb|,
作AD∥BC,CD⊥AD于点D,BE⊥AD于点E,则∠BAD=45°.
设||=150,则||=75(-).
∴||=||=||=75,||=75.
从而||=150,∠CAD=30°.
∴|vb|=150km/h,方向为北偏西60°.
题型突破
03
例4. 如图,物体W的质量为50 kg,用绳子将物体W悬挂在两面墙之间,已知两面墙之间的距离AB=10 m(AB为水平线),AC=6 m,BC=8 m,求AC,BC上所受的力的大小(g取9.8 m/s2).
题型3 向量在物理学中的应用
题型突破
03
题型3 向量在物理学中的应用
题型突破
03
解题通法
用向量方法解决物理问题的步骤
(1)把物理问题中的相关量用向量表示.
(2)转化为向量问题的模型,通过向量运算使问题解决.
(3)结果还原为物理问题.
题型3 向量在物理学中的应用
当堂检测
part 04
当堂检测
04
当堂检测
04
ABC
当堂检测
04
当堂检测
04
当堂检测
04
当堂检测
04
当堂检测
04
当堂检测
04
老师名字
谢谢观看
learn to report
