【单元测试卷】第4章 几何图形初步(含答案) 2024-2025学年数学沪科版七年级上册
文档属性
| 名称 | 【单元测试卷】第4章 几何图形初步(含答案) 2024-2025学年数学沪科版七年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 282.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-19 00:00:00 | ||
图片预览


文档简介
数学 第4章 几何图形初步
(时间:100分钟 分值:150分)
一、选择题(本大题共10小题,每小题4分,满分40分)
每小题都给出A、B、C、D四个选项,其中只有一个是正确的,请把正确答案的代号填在下表中.
题号 1 2 3 4 5 6 7 8 9 10
答案
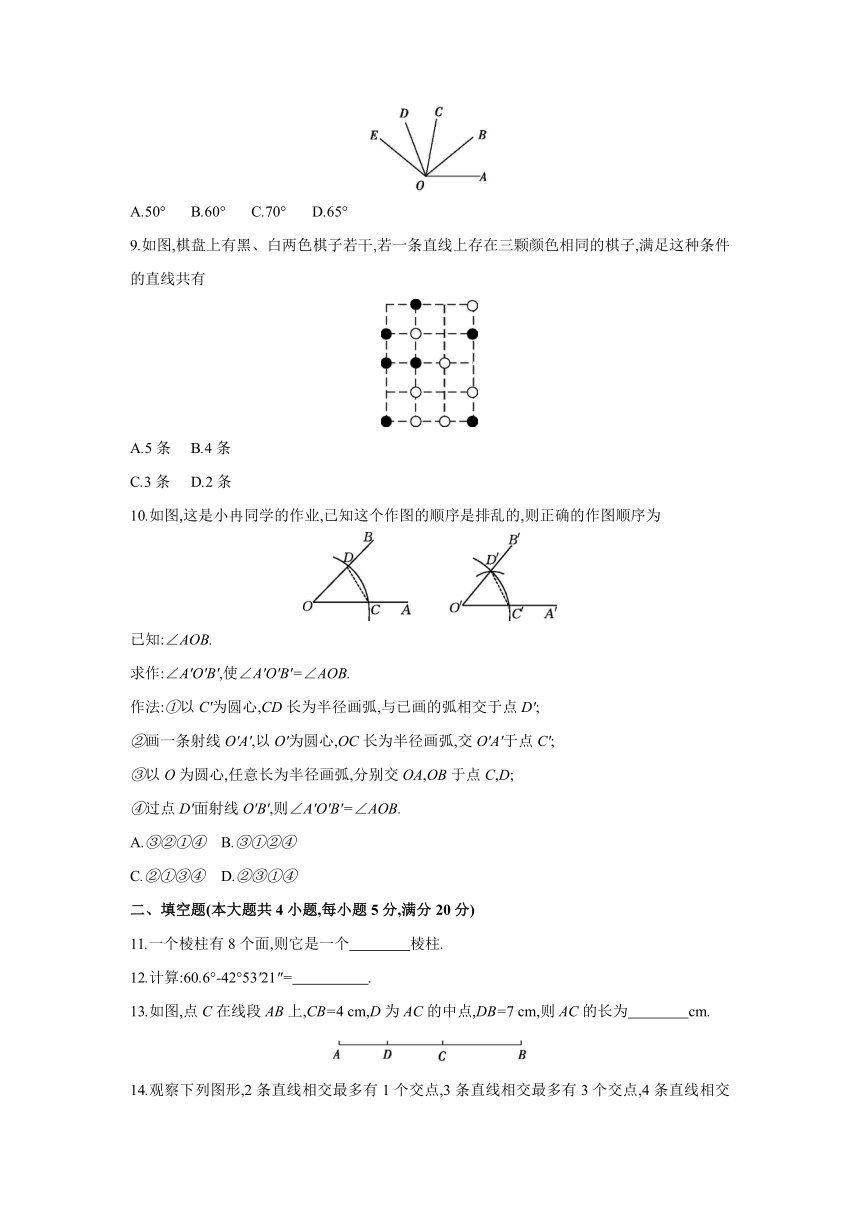
1.若一个几何体恰好可以无缝隙地以3个不同形状的“姿势”穿过如图所示的“墙”上的3个空洞,则该几何体为
A. B. C. D.
2.将一个三棱柱展开,其展开图是
A B C D
3.下列三个日常现象:
其中,可以用“两点之间线段最短”来解释的是
A.① B.②③ C.③ D.②
4.如图,1时30分的时候,钟表的时针与分针所组成的小于平角的角的度数是
A.120°
B.125°
C.135°
D.150°
5.如图,下列说法错误的是
A.∠DAO也可用∠DAC表示
B.∠COB也可用∠O表示
C.∠2也可用∠OBC表示
D.∠CDB也可用∠1表示
6.已知点C在直线AB上,若AC=4 cm,BC=6 cm,E、F分别为线段AC、BC的中点,则EF的长为
A.5 cm B.3 cm
C.5 cm或3 cm D.5 cm或1 cm
7.如图,在灯塔O处观测到轮船A位于北偏西55°的方向,同时轮船B在南偏东15°的方向,那么∠AOB的度数为
A.100° B.105° C.125° D.140°
8.如图,OB是∠AOC的平分线,OD是∠COE的平分线,若∠AOB=40°,∠COE=60°,则∠BOD的度数为
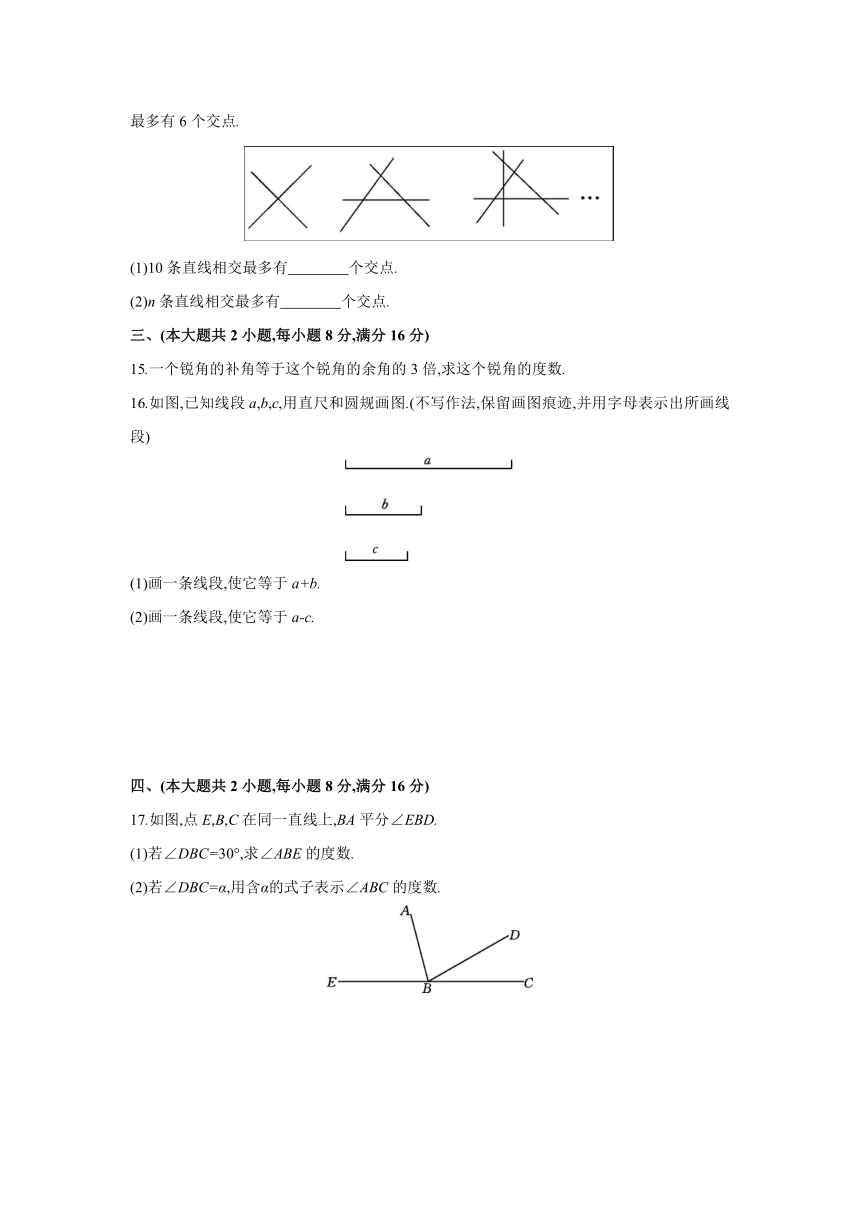
A.50° B.60° C.70° D.65°
9.如图,棋盘上有黑、白两色棋子若干,若一条直线上存在三颗颜色相同的棋子,满足这种条件的直线共有
A.5条 B.4条
C.3条 D.2条
10.如图,这是小冉同学的作业,已知这个作图的顺序是排乱的,则正确的作图顺序为
已知:∠AOB.
求作:∠A'O'B',使∠A'O'B'=∠AOB.
作法:①以C'为圆心,CD长为半径画弧,与已画的弧相交于点D';
②画一条射线O'A',以O'为圆心,OC长为半径画弧,交O'A'于点C';
③以O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
④过点D'面射线O'B',则∠A'O'B'=∠AOB.
A.③②①④ B.③①②④
C.②①③④ D.②③①④
二、填空题(本大题共4小题,每小题5分,满分20分)
11.一个棱柱有8个面,则它是一个 棱柱.
12.计算:60.6°-42°53'21″= .
13.如图,点C在线段AB上,CB=4 cm,D为AC的中点,DB=7 cm,则AC的长为 cm.
14.观察下列图形,2条直线相交最多有1个交点,3条直线相交最多有3个交点,4条直线相交最多有6个交点.
(1)10条直线相交最多有 个交点.
(2)n条直线相交最多有 个交点.
三、(本大题共2小题,每小题8分,满分16分)
15.一个锐角的补角等于这个锐角的余角的3倍,求这个锐角的度数.
16.如图,已知线段a,b,c,用直尺和圆规画图.(不写作法,保留画图痕迹,并用字母表示出所画线段)
(1)画一条线段,使它等于a+b.
(2)画一条线段,使它等于a-c.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,点E,B,C在同一直线上,BA平分∠EBD.
(1)若∠DBC=30°,求∠ABE的度数.
(2)若∠DBC=α,用含α的式子表示∠ABC的度数.
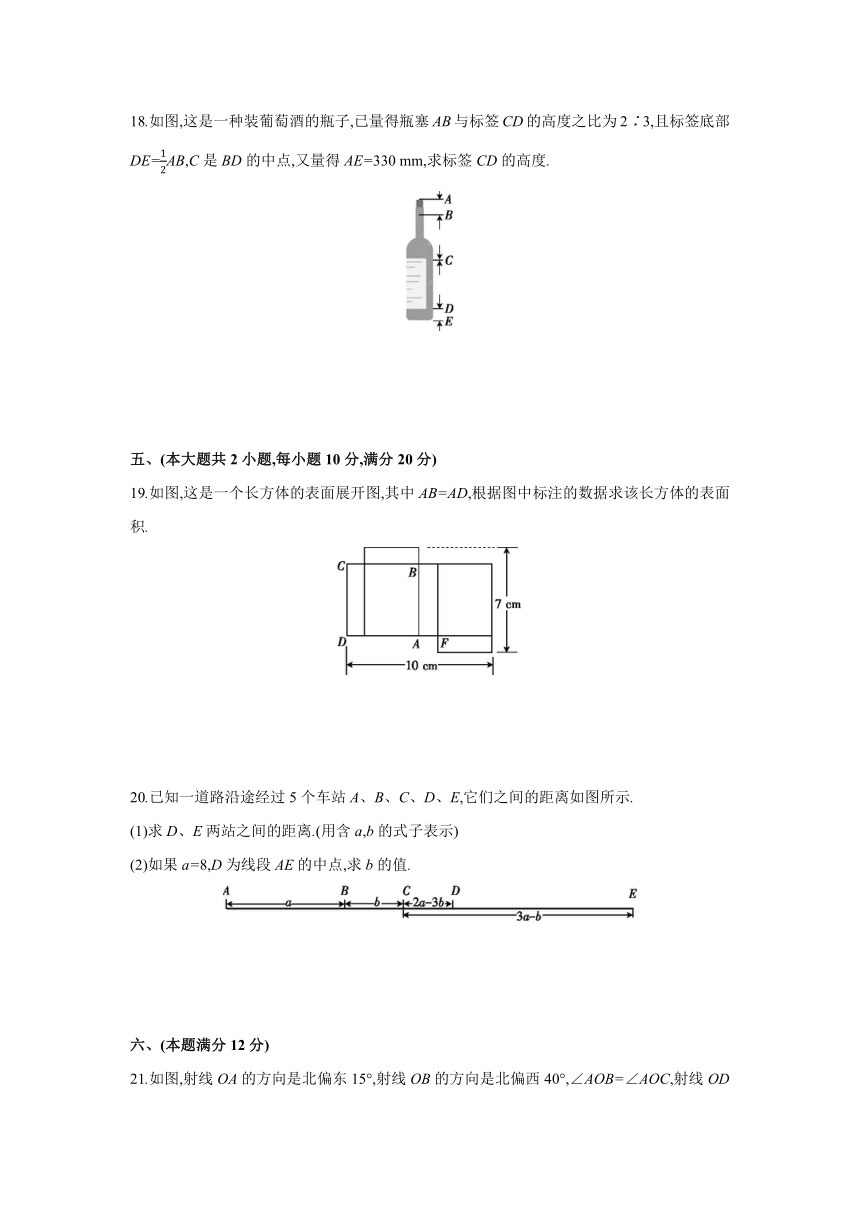
18.如图,这是一种装葡萄酒的瓶子,已量得瓶塞AB与标签CD的高度之比为2∶3,且标签底部DE=AB,C是BD的中点,又量得AE=330 mm,求标签CD的高度.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,这是一个长方体的表面展开图,其中AB=AD,根据图中标注的数据求该长方体的表面积.
20.已知一道路沿途经过5个车站A、B、C、D、E,它们之间的距离如图所示.
(1)求D、E两站之间的距离.(用含a,b的式子表示)
(2)如果a=8,D为线段AE的中点,求b的值.
六、(本题满分12分)
21.如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.
(1)射线OC的方向是 .
(2)求∠COD的度数.
(3)若射线OE平分∠COD,求∠AOE的度数.
七、(本题满分12分)
22.如图,已知线段AB=24,动点P从点A出发,以每秒2个单位长度的速度沿射线AB方向运动,运动时间为t(t>0)秒,M为AP的中点.
(1)当t=3时,求线MB的长度.
(2)当t为何值时,P恰好是MB的中点
(3)当t为何值时,AM=2PB
八、(本题满分14分)
23.如图1,已知线段AB=36 cm,CD=6 cm,线段CD在线段AB上运动(点C不与点A重合),E,F分别是AC,BD的中点.
(1)若AC=10 cm,则EF= cm.
(2)当线段CD在线段AB上运动时,试判断线段EF的长度是否会发生变化,如果不变,请求出线段EF的长度;如果变化,请说明理由.
(3)我们发现角的很多规律和线段一样,如图2,已知∠COD在∠AOB内部转动,OE,OF分别平分∠AOC和∠BOD.类比以上发现的线段的规律,当∠EOF=80°,∠COD=30°时,求∠AOB的度数.
图1 图2
参考答案
1.A 2.A 3.D 4.C 5.B 6.D 7.D 8.C 9.A 10.A
11.六 12.17°42'39″ 13.6
14.(1)45(2分) (2)(3分)
提示:(1)2条直线相交最多有1个交点,
3条直线相交最多有1+2=3个交点,
4条直线相交最多有1+2+3=6个交点,
5条直线相交最多有1+2+3+4=10个交点,
…
10条直线相交最多有1+2+3+4+5+6+7+8+9=45个交点.
(2)n条直线相交最多有1+2+3+…+n-1=个交点.
15.解:设这个角为x°,则根据题意得180-x=3(90-x), 4分
解得x=45. 7分
答:这个锐角的度数45°. 8分
16.解:(1)如图1,线段AC即所求.
图1
(2)如图2,线段AD即所求.
图2
17.解:(1)因为∠DBC=30°,
所以∠DBE=180°-∠DBC=150°.
因为BA平分∠EBD,
所以∠ABE=∠DBE=75°. 4分
(2)因为∠DBC=α,
所以∠DBE=180°-∠DBC=180°-α,
因为BA平分∠EBD,
所以∠DBA=∠DBE=90°-α,
所以∠ABC=∠DBA+∠DBC=90°-α+α=90°+α. 8分
18.解:设DE的长为x mm. 1分
由DE=AB,得AB=2DE=2x mm,
由AB∶CD=2∶3,AB=2x mm,得CD=3x mm. 2分
∵C是BD的中点,
∴BC=CD=3x mm. 3分
∵AE=330 mm,
∴AB+BC+CD+DE=2x+3x+3x+x=330, 6分
∴x=, 7分
∴标签CD的高度为110 mm. 8分
19.解:设AB=x cm,AF=y cm.
根据题意有 5分
解得
故AB的长为5 cm,AF的长为1 cm. 8分
所以长方体的表面积为10×6-1-1=58 cm2. 10分
20.解:(1)由线段的和差,得DE=CE-CD=(3a-b)-(2a-3b)=a+2b,
故D、E两站之间的距离是a+2b. 5分
(2)由D为线段AE的中点,得AD=DE, 6分
则a+b+2a-3b=a+2b,
即a=2b=8,解得b=4. 10分
21.解:(1)北偏东70°. 2分
(2)因为∠AOB=55°,∠AOC=∠AOB,
所以∠BOC=110°.
又因为OD是OB的反向延长线,
所以∠BOD=180°,
所以∠COD=180°-110°=70°. 7分
(3)因为∠COD=70°,OE平分∠COD,
所以∠COE=35°.
因为∠AOC=55°,
所以∠AOE=90°. 12分
22.解:(1)当t=3时,AP=3×2=6.
因为M为AP的中点,
所以AM=AP=×6=3,
所以MB=AB-AM=24-3=21. 4分
(2)因为M为AP的中点,
所以AM=MP=AP=×2t=t.
因为P是MB的中点,
所以MP=PB=t,
所以AB=3AM=3t=24,
所以t=8. 8分
(3)如图1,当点P在线段AB上时,AM=t,
图1
PB=AB-AP=24-2t,
所以t=2(24-2t),
解得t=. 10分
如图2,当点P在线段AB的延长线上时,AM=t,
图2
PB=AP-AB=2t-24,
所以t=2(2t-24),
解得t=16.
所以t=或t=16. 12分
23.解:(1)21. 3分
(2)当线段CD在线段AB上运动时,线段EF的长度不变,始终为21 cm,理由如下:
因为AB=36 cm,CD=6 cm,
所以AC+BD=AB-CD=30 cm.
因为E,F分别是AC,BD的中点,
所以EC=AC,DF=BD,
所以EC+DF=AC+BD=(AC+BD)=15(cm),
所以EF=EC+CD+DF=15+6=21(cm).
当线段CD在线段AB上运动时,线段EF的长度不变,EF=21 cm. 8分
(3)设∠AOE=α,∠BOF=β,
因为OE,OF分别平分∠AOC和∠BOD,
所以∠EOC=∠AOE=α,∠DOF=∠BOF=β,
所以∠EOF=∠EOC+∠COD+∠DOF.
因为∠EOF=80°,∠COD=30°,
所以80°=α+30°+β,
所以α+β=50°,
所以∠AOE+∠BOF=α+β=50°,
所以∠AOB=∠AOE+∠BOF+∠EOF=50°+80°=130°. 14分
(时间:100分钟 分值:150分)
一、选择题(本大题共10小题,每小题4分,满分40分)
每小题都给出A、B、C、D四个选项,其中只有一个是正确的,请把正确答案的代号填在下表中.
题号 1 2 3 4 5 6 7 8 9 10
答案
1.若一个几何体恰好可以无缝隙地以3个不同形状的“姿势”穿过如图所示的“墙”上的3个空洞,则该几何体为
A. B. C. D.
2.将一个三棱柱展开,其展开图是
A B C D
3.下列三个日常现象:
其中,可以用“两点之间线段最短”来解释的是
A.① B.②③ C.③ D.②
4.如图,1时30分的时候,钟表的时针与分针所组成的小于平角的角的度数是
A.120°
B.125°
C.135°
D.150°
5.如图,下列说法错误的是
A.∠DAO也可用∠DAC表示
B.∠COB也可用∠O表示
C.∠2也可用∠OBC表示
D.∠CDB也可用∠1表示
6.已知点C在直线AB上,若AC=4 cm,BC=6 cm,E、F分别为线段AC、BC的中点,则EF的长为
A.5 cm B.3 cm
C.5 cm或3 cm D.5 cm或1 cm
7.如图,在灯塔O处观测到轮船A位于北偏西55°的方向,同时轮船B在南偏东15°的方向,那么∠AOB的度数为
A.100° B.105° C.125° D.140°
8.如图,OB是∠AOC的平分线,OD是∠COE的平分线,若∠AOB=40°,∠COE=60°,则∠BOD的度数为
A.50° B.60° C.70° D.65°
9.如图,棋盘上有黑、白两色棋子若干,若一条直线上存在三颗颜色相同的棋子,满足这种条件的直线共有
A.5条 B.4条
C.3条 D.2条
10.如图,这是小冉同学的作业,已知这个作图的顺序是排乱的,则正确的作图顺序为
已知:∠AOB.
求作:∠A'O'B',使∠A'O'B'=∠AOB.
作法:①以C'为圆心,CD长为半径画弧,与已画的弧相交于点D';
②画一条射线O'A',以O'为圆心,OC长为半径画弧,交O'A'于点C';
③以O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
④过点D'面射线O'B',则∠A'O'B'=∠AOB.
A.③②①④ B.③①②④
C.②①③④ D.②③①④
二、填空题(本大题共4小题,每小题5分,满分20分)
11.一个棱柱有8个面,则它是一个 棱柱.
12.计算:60.6°-42°53'21″= .
13.如图,点C在线段AB上,CB=4 cm,D为AC的中点,DB=7 cm,则AC的长为 cm.
14.观察下列图形,2条直线相交最多有1个交点,3条直线相交最多有3个交点,4条直线相交最多有6个交点.
(1)10条直线相交最多有 个交点.
(2)n条直线相交最多有 个交点.
三、(本大题共2小题,每小题8分,满分16分)
15.一个锐角的补角等于这个锐角的余角的3倍,求这个锐角的度数.
16.如图,已知线段a,b,c,用直尺和圆规画图.(不写作法,保留画图痕迹,并用字母表示出所画线段)
(1)画一条线段,使它等于a+b.
(2)画一条线段,使它等于a-c.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,点E,B,C在同一直线上,BA平分∠EBD.
(1)若∠DBC=30°,求∠ABE的度数.
(2)若∠DBC=α,用含α的式子表示∠ABC的度数.
18.如图,这是一种装葡萄酒的瓶子,已量得瓶塞AB与标签CD的高度之比为2∶3,且标签底部DE=AB,C是BD的中点,又量得AE=330 mm,求标签CD的高度.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,这是一个长方体的表面展开图,其中AB=AD,根据图中标注的数据求该长方体的表面积.
20.已知一道路沿途经过5个车站A、B、C、D、E,它们之间的距离如图所示.
(1)求D、E两站之间的距离.(用含a,b的式子表示)
(2)如果a=8,D为线段AE的中点,求b的值.
六、(本题满分12分)
21.如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.
(1)射线OC的方向是 .
(2)求∠COD的度数.
(3)若射线OE平分∠COD,求∠AOE的度数.
七、(本题满分12分)
22.如图,已知线段AB=24,动点P从点A出发,以每秒2个单位长度的速度沿射线AB方向运动,运动时间为t(t>0)秒,M为AP的中点.
(1)当t=3时,求线MB的长度.
(2)当t为何值时,P恰好是MB的中点
(3)当t为何值时,AM=2PB
八、(本题满分14分)
23.如图1,已知线段AB=36 cm,CD=6 cm,线段CD在线段AB上运动(点C不与点A重合),E,F分别是AC,BD的中点.
(1)若AC=10 cm,则EF= cm.
(2)当线段CD在线段AB上运动时,试判断线段EF的长度是否会发生变化,如果不变,请求出线段EF的长度;如果变化,请说明理由.
(3)我们发现角的很多规律和线段一样,如图2,已知∠COD在∠AOB内部转动,OE,OF分别平分∠AOC和∠BOD.类比以上发现的线段的规律,当∠EOF=80°,∠COD=30°时,求∠AOB的度数.
图1 图2
参考答案
1.A 2.A 3.D 4.C 5.B 6.D 7.D 8.C 9.A 10.A
11.六 12.17°42'39″ 13.6
14.(1)45(2分) (2)(3分)
提示:(1)2条直线相交最多有1个交点,
3条直线相交最多有1+2=3个交点,
4条直线相交最多有1+2+3=6个交点,
5条直线相交最多有1+2+3+4=10个交点,
…
10条直线相交最多有1+2+3+4+5+6+7+8+9=45个交点.
(2)n条直线相交最多有1+2+3+…+n-1=个交点.
15.解:设这个角为x°,则根据题意得180-x=3(90-x), 4分
解得x=45. 7分
答:这个锐角的度数45°. 8分
16.解:(1)如图1,线段AC即所求.
图1
(2)如图2,线段AD即所求.
图2
17.解:(1)因为∠DBC=30°,
所以∠DBE=180°-∠DBC=150°.
因为BA平分∠EBD,
所以∠ABE=∠DBE=75°. 4分
(2)因为∠DBC=α,
所以∠DBE=180°-∠DBC=180°-α,
因为BA平分∠EBD,
所以∠DBA=∠DBE=90°-α,
所以∠ABC=∠DBA+∠DBC=90°-α+α=90°+α. 8分
18.解:设DE的长为x mm. 1分
由DE=AB,得AB=2DE=2x mm,
由AB∶CD=2∶3,AB=2x mm,得CD=3x mm. 2分
∵C是BD的中点,
∴BC=CD=3x mm. 3分
∵AE=330 mm,
∴AB+BC+CD+DE=2x+3x+3x+x=330, 6分
∴x=, 7分
∴标签CD的高度为110 mm. 8分
19.解:设AB=x cm,AF=y cm.
根据题意有 5分
解得
故AB的长为5 cm,AF的长为1 cm. 8分
所以长方体的表面积为10×6-1-1=58 cm2. 10分
20.解:(1)由线段的和差,得DE=CE-CD=(3a-b)-(2a-3b)=a+2b,
故D、E两站之间的距离是a+2b. 5分
(2)由D为线段AE的中点,得AD=DE, 6分
则a+b+2a-3b=a+2b,
即a=2b=8,解得b=4. 10分
21.解:(1)北偏东70°. 2分
(2)因为∠AOB=55°,∠AOC=∠AOB,
所以∠BOC=110°.
又因为OD是OB的反向延长线,
所以∠BOD=180°,
所以∠COD=180°-110°=70°. 7分
(3)因为∠COD=70°,OE平分∠COD,
所以∠COE=35°.
因为∠AOC=55°,
所以∠AOE=90°. 12分
22.解:(1)当t=3时,AP=3×2=6.
因为M为AP的中点,
所以AM=AP=×6=3,
所以MB=AB-AM=24-3=21. 4分
(2)因为M为AP的中点,
所以AM=MP=AP=×2t=t.
因为P是MB的中点,
所以MP=PB=t,
所以AB=3AM=3t=24,
所以t=8. 8分
(3)如图1,当点P在线段AB上时,AM=t,
图1
PB=AB-AP=24-2t,
所以t=2(24-2t),
解得t=. 10分
如图2,当点P在线段AB的延长线上时,AM=t,
图2
PB=AP-AB=2t-24,
所以t=2(2t-24),
解得t=16.
所以t=或t=16. 12分
23.解:(1)21. 3分
(2)当线段CD在线段AB上运动时,线段EF的长度不变,始终为21 cm,理由如下:
因为AB=36 cm,CD=6 cm,
所以AC+BD=AB-CD=30 cm.
因为E,F分别是AC,BD的中点,
所以EC=AC,DF=BD,
所以EC+DF=AC+BD=(AC+BD)=15(cm),
所以EF=EC+CD+DF=15+6=21(cm).
当线段CD在线段AB上运动时,线段EF的长度不变,EF=21 cm. 8分
(3)设∠AOE=α,∠BOF=β,
因为OE,OF分别平分∠AOC和∠BOD,
所以∠EOC=∠AOE=α,∠DOF=∠BOF=β,
所以∠EOF=∠EOC+∠COD+∠DOF.
因为∠EOF=80°,∠COD=30°,
所以80°=α+30°+β,
所以α+β=50°,
所以∠AOE+∠BOF=α+β=50°,
所以∠AOB=∠AOE+∠BOF+∠EOF=50°+80°=130°. 14分
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
