浙江省宁波市鄞州区鄞州实验中学2024-2025学年九年级上学期第五次模拟数学试卷(图片版,无答案)
文档属性
| 名称 | 浙江省宁波市鄞州区鄞州实验中学2024-2025学年九年级上学期第五次模拟数学试卷(图片版,无答案) | 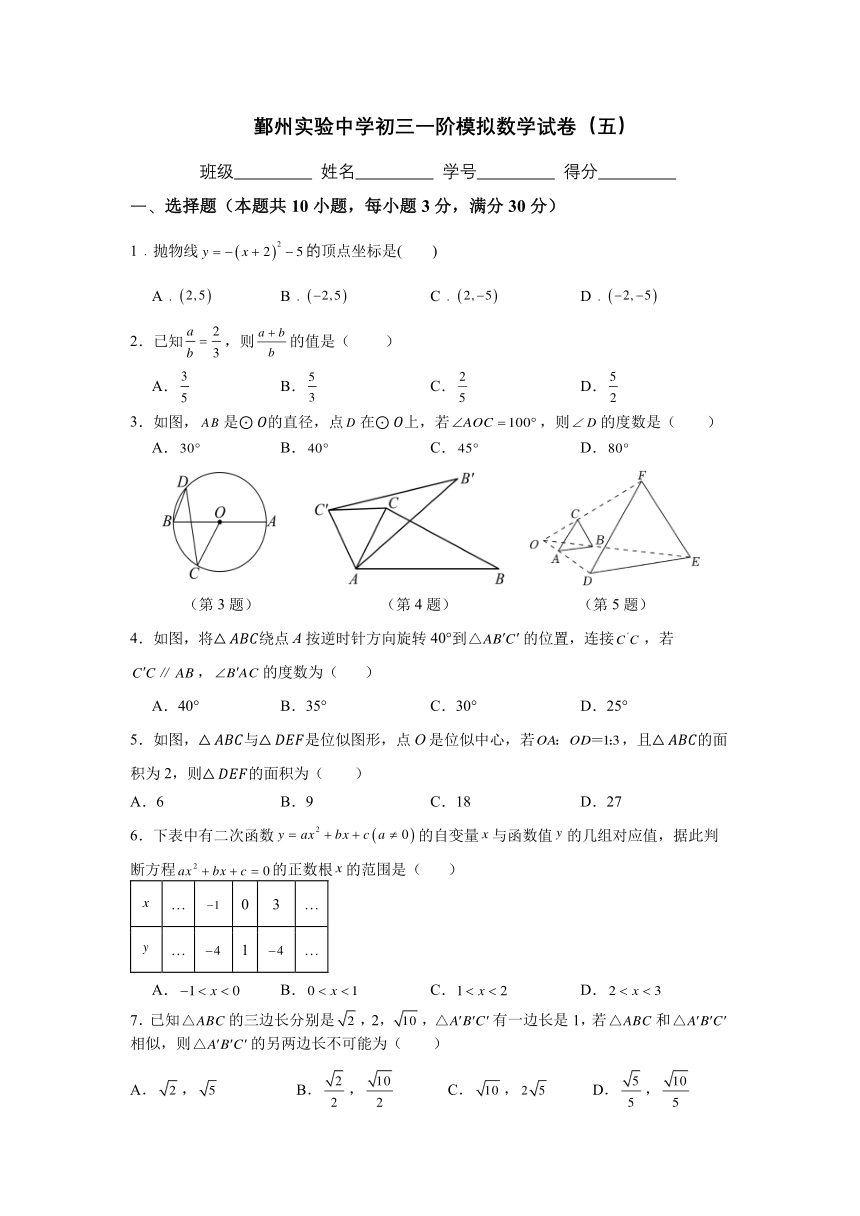 | |
| 格式 | |||
| 文件大小 | 728.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-19 18:35:18 | ||
图片预览



文档简介
鄞州实验中学初三一阶模拟数学试卷(五)
班级 姓名 学号 得分
一、选择题(本题共 10小题,每小题 3分,满分 30分)
2
1.抛物线 y = ( x + 2 ) 5的顶点坐标是( )
A. ( 2, 5 ) B. ( 2, 5 ) C. ( 2, 5 ) D. ( 2, 5 )
a 2 a + b
2.已知 = ,则 的值是( )
b 3 b
3 5 2 5
A. B. C. D.
5 3 5 2
3.如图, AB 是⊙ 的直径,点D 在⊙ 上,若 AOC = 100 ,则 D 的度数是( )
A.30 B. 40 C. 45 D.80
(第 3 题) (第 4 题) (第 5 题)
4.如图,将△ 绕点 A按逆时针方向旋转 40°到△AB C 的位置,连接 C C ,若
C C∥ AB , B AC 的度数为( )
A.40° B.35° C.30° D.25°
5.如图,△ 与△ 是位似图形,点 O是位似中心,若OA:OD=1:3,且△ 的面
积为 2,则△ 的面积为( )
A.6 B.9 C.18 D.27
2
6.下表中有二次函数 y = ax + bx + c (a 0 )的自变量 x 与函数值 y 的几组对应值,据此判
断方程 2ax + bx + c = 0的正数根 x 的范围是( )
x … 1 0 3 …
y … 4 1 4 …
A. 1 x 0 B.0 x 1 C.1 x 2 D.2 x 3
7.已知△ABC 的三边长分别是 2 ,2, 10 ,△A B C 有一边长是 1,若△ABC 和△A B C
相似,则△A B C 的另两边长不可能为( )
2 10 5 10
A. 2 , 5 B. , C. 10 , 2 5 D. ,
2 2 5 5
8.如图,在△ABC 中,BC = 3, AC = 4 , C = 90 ,以点 B 为圆心,BC 长为半径画弧,
1
与 AB 交于点 D ,再分别以 A ,D 为圆心,大于 AD 的长为半径画弧,两弧交于点M ,N ,
2
作直线MN ,分别交 AC , AB 于点 E , F ,则 AE 的长度为( )
5 5 10
A. B.3 C. D.
2 4 3
(第 8 题) (第 9 题)
9.如图, ABC 是⊙ 的内接三角形, AB = AC , BAC = 120 ,D 是 BC 边上一点,连接
AD 并延长交⊙ 于点 E .若 AD = 2 , DE = 3 ,则⊙ 的半径为 ( )
3
A. 10 B. 10 C.5 D. 2 3
2
10.在平面直角坐标系 xOy 中,抛物线 2y = m(x + 2) + k 与 x轴交于 ( x , 01 ), ( x , 02 )两点,其
中 x x1 2 ,将此抛物线向上平移,与 x轴交于 ( x , 0 ), ( x , 0 )两点,其中 x x3 4 3 4 ,下面结论
正确的是( )
A.当m 0, x + x = x + x , x x x x1 2 3 4 2 1 4 3 B.当m 0, x + x x + x , x x = x x1 2 3 4 2 1 4 3
C.当m 0, x + x = x + x , x x x x1 2 3 4 2 1 4 3 D.当m 0 , x + x x + x , x x = x x1 2 3 4 2 1 4 3
二、填空题(本题共 6小题,每小题 3分,满分 18分)
11.正八边形每个内角的度数为
12.写出一个二次函数,使其图象满足:①开口向下;②与 y 轴交于点 (0, 2) ,这个二次函数
的解析式可以是__________
5 + 1
13.己知线段 AB = ,点 P是它的黄金分割点,则 BP 的长为
2
14.如图,AB ,CD 是⊙ 的两条平行弦,且 AB = 4 ,CD = 6 ,AB ,CD 之间的距离为 5,
则⊙ 的直径是
(第 14 题) (第 15 题)
15.如图,扇形OAB 的圆心角为 60 ,OA = 4cm ,过点 A 作 AD ⊥ OB 于点 D ,以O 为圆心,
OD 的长为半径画弧交OA 于点C ,则图中阴影部分的面积是__________.
16.在平行四边形 ABCD 中, AB = 4 ,BC = 6 ,点 E 是 BC 边上的点,连接 AE ,将 ABE
沿 AE 翻折至 AFE ,连接CF .
1
(1)如图 1,连接 BF ,若点 E 为 BC 边中点,且CF = AB 时,则 ABF = __________
2
(2)如图 2,连接 DF ,当点 D 、 F 、 E 三点共线时,恰有 DCF = ADF ,则CF 的长为
__________
三、解答题(本题 8大题,17—21每题 8分,22—23每题 10分,24题 12 分
共,满分 72分)
17.已知抛物线经过点 (1, 0) , (3, 0),且有最大值 4.
(1)求抛物线的表达式;
(2)求该抛物线对称轴;
(3)若 1 x 3 ,求函数值 y 的取值范围.
18.如图,在平行四边形 ABCD 中,过点 A 作 AE ⊥ BC ,垂足为 E ,连接 DE , F 为线段
DE 上一点,且 AFE = B .
(1)求证: ADF∽ DEC
(2)若 AB = 4 , BC = 3 3 , AF = 2 3 ,求 AE 的长.
19.如图在5 5的网格中,△ 的顶点都在格点上,仅用无刻度的直尺在给定的网格中
分别按下列要求画图.(请保留画图痕迹,画图过程用虚线表示,画图结果用实线表示)
(1)在图 1 中,画出△ 的重心 G;
(2)在图 2 中,画线段CE ,点 E在 AB 上,使得 △ ∶ △ = 3 ∶ 4;
(3)图 3 中,在△ 内寻找一格点 N,使 ANB = 2 C ,并标注点 N的位置.
20.已知:如图,在△ 中, AB = AC = 4 ,以腰 AB 为直径作半圆 O,分别交BC , AC
于点 D,E.
(1)求证: BD = DC .
(2)若 BAC = 50 ,求弧 AE 的度数及长度.
21.如图,△ 内接于⊙ , ABC 90 ,△ 的外角 EAC 的平分线交⊙ 于
点 D,连接 DB , DC , DB 交 AC 于点 F.
(1)求证:△ 是等腰三角形.
(2)若 DA = DF ,求证: 2BC = DC BF .
22.已知二次函数 2y = x + bx + c .
(1)当b = 2, c = 3时,
①求该函数图象的顶点坐标;
②设计一种平移方案,使得该函数图像经过原点;
(2)当 x 0 时,y的最小值为 8 ;当 x 0 时,y的最小值为 9,求二次函数的表达式.
23.根据素材解决问题.
设计货船通过圆形拱桥的方案
图 1 中有一座圆拱石桥,图 2 是其圆形桥拱的示意图,测得水面宽
AB=16m,拱顶离水面的距离 CD=4m.
素材 1
如图 3,一艘货船露出水面部分的横截面为矩形 EFGH,测得 EF=3m,
EH=10m.因水深足够,货船可以根据需要运载货物.据调查,船身下降
1
的高度 y(米)与货船增加的载重量 x (吨)满足函数关系式 y= x.
素材 2 100
问题解决
任务 1 确定桥拱半径 求圆形桥拱的半径.
根据图 3 状态,货船能否通过圆形桥拱?若能,最多还
任务 2 拟定设计方案 能卸载多少吨货物?若不能,至少要增加多少吨货物才
能通过?
24.如图,△ 内接于⊙O ,过点O 作OH ⊥ BC 于点 H ,延长OH 交⊙O 于点D ,连接
AD 、 BD , AD 与 BC 交于点 E , AD = 9
(1)求证: BAD = CAD .
(2)若OH = DH .
①求 BAC 的度数.
②若⊙O 的半径为6,求DE 的长.
(3)设 BD = x , AB CE = y ,求 y 关于 x 的函数表达式.
班级 姓名 学号 得分
一、选择题(本题共 10小题,每小题 3分,满分 30分)
2
1.抛物线 y = ( x + 2 ) 5的顶点坐标是( )
A. ( 2, 5 ) B. ( 2, 5 ) C. ( 2, 5 ) D. ( 2, 5 )
a 2 a + b
2.已知 = ,则 的值是( )
b 3 b
3 5 2 5
A. B. C. D.
5 3 5 2
3.如图, AB 是⊙ 的直径,点D 在⊙ 上,若 AOC = 100 ,则 D 的度数是( )
A.30 B. 40 C. 45 D.80
(第 3 题) (第 4 题) (第 5 题)
4.如图,将△ 绕点 A按逆时针方向旋转 40°到△AB C 的位置,连接 C C ,若
C C∥ AB , B AC 的度数为( )
A.40° B.35° C.30° D.25°
5.如图,△ 与△ 是位似图形,点 O是位似中心,若OA:OD=1:3,且△ 的面
积为 2,则△ 的面积为( )
A.6 B.9 C.18 D.27
2
6.下表中有二次函数 y = ax + bx + c (a 0 )的自变量 x 与函数值 y 的几组对应值,据此判
断方程 2ax + bx + c = 0的正数根 x 的范围是( )
x … 1 0 3 …
y … 4 1 4 …
A. 1 x 0 B.0 x 1 C.1 x 2 D.2 x 3
7.已知△ABC 的三边长分别是 2 ,2, 10 ,△A B C 有一边长是 1,若△ABC 和△A B C
相似,则△A B C 的另两边长不可能为( )
2 10 5 10
A. 2 , 5 B. , C. 10 , 2 5 D. ,
2 2 5 5
8.如图,在△ABC 中,BC = 3, AC = 4 , C = 90 ,以点 B 为圆心,BC 长为半径画弧,
1
与 AB 交于点 D ,再分别以 A ,D 为圆心,大于 AD 的长为半径画弧,两弧交于点M ,N ,
2
作直线MN ,分别交 AC , AB 于点 E , F ,则 AE 的长度为( )
5 5 10
A. B.3 C. D.
2 4 3
(第 8 题) (第 9 题)
9.如图, ABC 是⊙ 的内接三角形, AB = AC , BAC = 120 ,D 是 BC 边上一点,连接
AD 并延长交⊙ 于点 E .若 AD = 2 , DE = 3 ,则⊙ 的半径为 ( )
3
A. 10 B. 10 C.5 D. 2 3
2
10.在平面直角坐标系 xOy 中,抛物线 2y = m(x + 2) + k 与 x轴交于 ( x , 01 ), ( x , 02 )两点,其
中 x x1 2 ,将此抛物线向上平移,与 x轴交于 ( x , 0 ), ( x , 0 )两点,其中 x x3 4 3 4 ,下面结论
正确的是( )
A.当m 0, x + x = x + x , x x x x1 2 3 4 2 1 4 3 B.当m 0, x + x x + x , x x = x x1 2 3 4 2 1 4 3
C.当m 0, x + x = x + x , x x x x1 2 3 4 2 1 4 3 D.当m 0 , x + x x + x , x x = x x1 2 3 4 2 1 4 3
二、填空题(本题共 6小题,每小题 3分,满分 18分)
11.正八边形每个内角的度数为
12.写出一个二次函数,使其图象满足:①开口向下;②与 y 轴交于点 (0, 2) ,这个二次函数
的解析式可以是__________
5 + 1
13.己知线段 AB = ,点 P是它的黄金分割点,则 BP 的长为
2
14.如图,AB ,CD 是⊙ 的两条平行弦,且 AB = 4 ,CD = 6 ,AB ,CD 之间的距离为 5,
则⊙ 的直径是
(第 14 题) (第 15 题)
15.如图,扇形OAB 的圆心角为 60 ,OA = 4cm ,过点 A 作 AD ⊥ OB 于点 D ,以O 为圆心,
OD 的长为半径画弧交OA 于点C ,则图中阴影部分的面积是__________.
16.在平行四边形 ABCD 中, AB = 4 ,BC = 6 ,点 E 是 BC 边上的点,连接 AE ,将 ABE
沿 AE 翻折至 AFE ,连接CF .
1
(1)如图 1,连接 BF ,若点 E 为 BC 边中点,且CF = AB 时,则 ABF = __________
2
(2)如图 2,连接 DF ,当点 D 、 F 、 E 三点共线时,恰有 DCF = ADF ,则CF 的长为
__________
三、解答题(本题 8大题,17—21每题 8分,22—23每题 10分,24题 12 分
共,满分 72分)
17.已知抛物线经过点 (1, 0) , (3, 0),且有最大值 4.
(1)求抛物线的表达式;
(2)求该抛物线对称轴;
(3)若 1 x 3 ,求函数值 y 的取值范围.
18.如图,在平行四边形 ABCD 中,过点 A 作 AE ⊥ BC ,垂足为 E ,连接 DE , F 为线段
DE 上一点,且 AFE = B .
(1)求证: ADF∽ DEC
(2)若 AB = 4 , BC = 3 3 , AF = 2 3 ,求 AE 的长.
19.如图在5 5的网格中,△ 的顶点都在格点上,仅用无刻度的直尺在给定的网格中
分别按下列要求画图.(请保留画图痕迹,画图过程用虚线表示,画图结果用实线表示)
(1)在图 1 中,画出△ 的重心 G;
(2)在图 2 中,画线段CE ,点 E在 AB 上,使得 △ ∶ △ = 3 ∶ 4;
(3)图 3 中,在△ 内寻找一格点 N,使 ANB = 2 C ,并标注点 N的位置.
20.已知:如图,在△ 中, AB = AC = 4 ,以腰 AB 为直径作半圆 O,分别交BC , AC
于点 D,E.
(1)求证: BD = DC .
(2)若 BAC = 50 ,求弧 AE 的度数及长度.
21.如图,△ 内接于⊙ , ABC 90 ,△ 的外角 EAC 的平分线交⊙ 于
点 D,连接 DB , DC , DB 交 AC 于点 F.
(1)求证:△ 是等腰三角形.
(2)若 DA = DF ,求证: 2BC = DC BF .
22.已知二次函数 2y = x + bx + c .
(1)当b = 2, c = 3时,
①求该函数图象的顶点坐标;
②设计一种平移方案,使得该函数图像经过原点;
(2)当 x 0 时,y的最小值为 8 ;当 x 0 时,y的最小值为 9,求二次函数的表达式.
23.根据素材解决问题.
设计货船通过圆形拱桥的方案
图 1 中有一座圆拱石桥,图 2 是其圆形桥拱的示意图,测得水面宽
AB=16m,拱顶离水面的距离 CD=4m.
素材 1
如图 3,一艘货船露出水面部分的横截面为矩形 EFGH,测得 EF=3m,
EH=10m.因水深足够,货船可以根据需要运载货物.据调查,船身下降
1
的高度 y(米)与货船增加的载重量 x (吨)满足函数关系式 y= x.
素材 2 100
问题解决
任务 1 确定桥拱半径 求圆形桥拱的半径.
根据图 3 状态,货船能否通过圆形桥拱?若能,最多还
任务 2 拟定设计方案 能卸载多少吨货物?若不能,至少要增加多少吨货物才
能通过?
24.如图,△ 内接于⊙O ,过点O 作OH ⊥ BC 于点 H ,延长OH 交⊙O 于点D ,连接
AD 、 BD , AD 与 BC 交于点 E , AD = 9
(1)求证: BAD = CAD .
(2)若OH = DH .
①求 BAC 的度数.
②若⊙O 的半径为6,求DE 的长.
(3)设 BD = x , AB CE = y ,求 y 关于 x 的函数表达式.
同课章节目录
