2.4.3第2课时 添括号 课件(共11张PPT)
文档属性
| 名称 | 2.4.3第2课时 添括号 课件(共11张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 305.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-20 16:38:39 | ||
图片预览




文档简介
(共11张PPT)
第2章 整式的加减
2.4.3 去括号和添括号
第2课时 添括号
随堂演练
课堂小结
获取新知
知识回顾
例题讲解
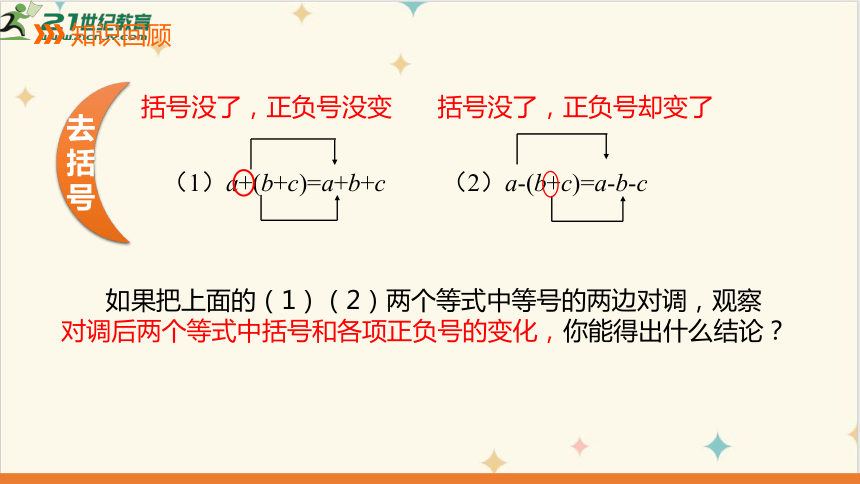
(1)a+(b+c)=a+b+c (2)a-(b+c)=a-b-c
括号没了,正负号没变
括号没了,正负号却变了
知识回顾
去括号
如果把上面的(1)(2)两个等式中等号的两边对调,观察对调后两个等式中括号和各项正负号的变化,你能得出什么结论?
获取新知
(1)a+b+c=a+(b+c) . (2)a-b-c=a-(b+c) .
正负号均不变
正负号均改变
添括号法则
1.所添括号前面是“+”号,括到括号里的各项都不改变正负号;
2.所添括号前面是“-”号,括到括号里的各项都改变正负号.
添括号与去括号的过程正好相反,添括号是否正确,
可以用去括号检验!
做一做
在括号内填入适当的项:
(1)x2-x+1=x2-( )
(2) 2x2-3x-1=2x2+( )
(3) (a-b)-(c-d)=a-( )
x-1
-3x-1
第(3)小题去括号之后,才能完成哦!
解:(3)(a-b)-(c-d)=a-b-c+d=a-(b+c-d)
b+c-d
例1 计算:
(1)214a+47a+53a;
(2)214a-39a-61a.
解:(1)214a+47a+53a
=214a+(47a+53a)
=214a+100a
=314a;
适当添加括号,可使计算简便.
(2)214a-39a-61a
=214a-(39a+61a)
=214a-100a
=114a.
例题讲解
例2 把多项式x3-6x2y+12xy2-8y3+1写成两个整式的和,使其中一个不含字母x.
分析:写成两个整式的和,即( )+( )
要求:一个整式不含字母x,先找出多项式中不含字母x的项,
-8y3 、1,即这两项组成一个整式,另一个整式是x3-6x2y+12xy2,根据添括号法则完成.
解:(x3-6x2y+12xy2)+(-8y3+1)
如果写成两个整式的差,结果如何?试一试.
1.在括号里添上适当的项.
(1)-a2-ab+2b2=+( )
=-( ).
(2)3a-a2+4=3a+( )
=3a-( ).
2.x-y+m-n等于 ( )
A.(x-y)-(m-n) B.(x-y)-(m+n)
C.(x-y)+(m-n) D.(x+n)-(y-m)
随堂演练
C
-a2-ab+2b2
a2 + ab-2b2
-a2 + 4
a2 - 4
3.把多项式a2-2bc+b2-c2写成两个代数式差的形式使被减式中只含字母a,减式中不含字母a.
a2-(2bc-b2+c2)
课堂小结
知识点 添括号法则
所添括号前面是“+”号,括到括号里的各项都不改变正负号.
所添括号前面是“-”号,括到括号里的各项都改变正负号.
添括号与去括号是两个相反的过程,因此可以相互检验正误.
添括号与去括号都是只改变式子的形状,不改变式子的值,
属于多项式的恒等变形,即“形变而值不变“.
谢谢
第2章 整式的加减
2.4.3 去括号和添括号
第2课时 添括号
随堂演练
课堂小结
获取新知
知识回顾
例题讲解
(1)a+(b+c)=a+b+c (2)a-(b+c)=a-b-c
括号没了,正负号没变
括号没了,正负号却变了
知识回顾
去括号
如果把上面的(1)(2)两个等式中等号的两边对调,观察对调后两个等式中括号和各项正负号的变化,你能得出什么结论?
获取新知
(1)a+b+c=a+(b+c) . (2)a-b-c=a-(b+c) .
正负号均不变
正负号均改变
添括号法则
1.所添括号前面是“+”号,括到括号里的各项都不改变正负号;
2.所添括号前面是“-”号,括到括号里的各项都改变正负号.
添括号与去括号的过程正好相反,添括号是否正确,
可以用去括号检验!
做一做
在括号内填入适当的项:
(1)x2-x+1=x2-( )
(2) 2x2-3x-1=2x2+( )
(3) (a-b)-(c-d)=a-( )
x-1
-3x-1
第(3)小题去括号之后,才能完成哦!
解:(3)(a-b)-(c-d)=a-b-c+d=a-(b+c-d)
b+c-d
例1 计算:
(1)214a+47a+53a;
(2)214a-39a-61a.
解:(1)214a+47a+53a
=214a+(47a+53a)
=214a+100a
=314a;
适当添加括号,可使计算简便.
(2)214a-39a-61a
=214a-(39a+61a)
=214a-100a
=114a.
例题讲解
例2 把多项式x3-6x2y+12xy2-8y3+1写成两个整式的和,使其中一个不含字母x.
分析:写成两个整式的和,即( )+( )
要求:一个整式不含字母x,先找出多项式中不含字母x的项,
-8y3 、1,即这两项组成一个整式,另一个整式是x3-6x2y+12xy2,根据添括号法则完成.
解:(x3-6x2y+12xy2)+(-8y3+1)
如果写成两个整式的差,结果如何?试一试.
1.在括号里添上适当的项.
(1)-a2-ab+2b2=+( )
=-( ).
(2)3a-a2+4=3a+( )
=3a-( ).
2.x-y+m-n等于 ( )
A.(x-y)-(m-n) B.(x-y)-(m+n)
C.(x-y)+(m-n) D.(x+n)-(y-m)
随堂演练
C
-a2-ab+2b2
a2 + ab-2b2
-a2 + 4
a2 - 4
3.把多项式a2-2bc+b2-c2写成两个代数式差的形式使被减式中只含字母a,减式中不含字母a.
a2-(2bc-b2+c2)
课堂小结
知识点 添括号法则
所添括号前面是“+”号,括到括号里的各项都不改变正负号.
所添括号前面是“-”号,括到括号里的各项都改变正负号.
添括号与去括号是两个相反的过程,因此可以相互检验正误.
添括号与去括号都是只改变式子的形状,不改变式子的值,
属于多项式的恒等变形,即“形变而值不变“.
谢谢
同课章节目录
