第六章 数据的分析—八年级上册数学北师大版(2012)单元质检卷(A卷)(含详解)
文档属性
| 名称 | 第六章 数据的分析—八年级上册数学北师大版(2012)单元质检卷(A卷)(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-20 10:04:28 | ||
图片预览




文档简介
(11)数据的分析—八年级上册数学北师大版(2012)单元质检卷(A卷)
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.一组数据:31,32,35,37,35,这组数据的平均数和中位数分别是( )
A.34,34 B.35,35 C.34,35 D.35,34
2.如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲 乙 丙 丁
平均数() 186 182 186 182
方差 3.2 3.2 6.5 6.0
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A.丁 B.丙 C.乙 D.甲
3.如图所示的条形图描述了某车间工人日加工零件数的情况,则这些工人日加工零件数的平均数、中位数、众数分别是( )
A.6.4,10,4 B.6,6,6 C.6.4,6,6 D.6,6,10
4.数学兴趣小组成员小刚对自己的学习质量进行了测试.如图是他最近五次测试成绩(满分为100分)的折线统计图,那么其平均数和方差分别是( )
A.95分, B.96分, C.95分,10 D.96分,10
5.在学校演讲比赛中,10名选手的成绩折线统计图如图所示,则下列说法正确的是( )
A.最高分90 B.众数是5 C.中位数是90 D.平均分为87.5
6.下表是某中学阳光社团40名志愿者的年龄分布统计表.对于a,b取不同的值,下列关于年龄的统计量不会发生改变的是( )
年龄(岁) 12 13 14 15
频数(名) 11 19 a b
A.平均数、众数 B.中位数、平均数
C.众数、中位数 D.平均数、方差
7.某校举行以“我和我的祖国”为主题的演讲比赛,7位评委给某同学打分(满分10分),该同学的得分情况是8,6,8,7,8,5,7.对于该组数据,下列说法错误的是( )
A.平均数为7 B.众数为8 C.中位数为7 D.方差为2
8.已知一组数据,,,的平均数为6,则另一组数据,,,的平均数为( )
A.5 B.6 C.7 D.不确定
9.为了解“睡眠管理”落实情况,某初中学校随机调查50名学生每天平均睡眠时间(时间均保留整数),将样本数据绘制成统计图(如图),其中有两个数据被遮盖关于睡眠时间的统计量中,与被遮盖的数据无关的是( )
A.平均数 B.中位数 C.众数 D.方差
10.小庆、小铁、小娜、小萌四名同学均从1,2,3,4,5,6这六个数字中选出四个数字,玩猜数游戏.下列选项中,能确定该同学选出的四个数字含有1的是( )
A.小庆选出四个数字的方差等于 B.小铁选出四个数字的方差等于
C.小娜选出四个数字的平均数等于 D.小萌选出四个数字的极差等于4
二、填空题(每小题4分,共20分)
11.2024年全国两会提出:以科技创新推动产业创新,以前沿技术催生新产业、新模式、新动力,发展新质生产力,促进高质量发展.某学校数学社团使用问卷星APP发起了“人工智能(AI)知多少?”的问卷调查,把知道的程度由低到高分别记为1分、2分、3分、4分、5分.画出的扇形统计图如图所示,则近打分数的众数为______.
12.已知一组数据2,3,4,m,的众数为3,则平均数为______.
13.已知一组数据:4、3、2、m、n的众数为3,平均数为2,,则n的值为______.
14.已知一组正整数a,1,b,b,3有唯一众数8,中位数是5,则这一组数据的平均数为______.
15.若一组数据,,,…,的平均数为4,方差为2,则,,,…,的方差为__________.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)下表是某女子篮球队其中五名队员的身高情况:(单位:).
女篮队员 A B C D E
个人身高 176 a 207 192 191
个人身高与全队平均身高的差值 b c
(1)求出a,b,c的值;
(2)求该女子篮球队这五名队员的平均身高.
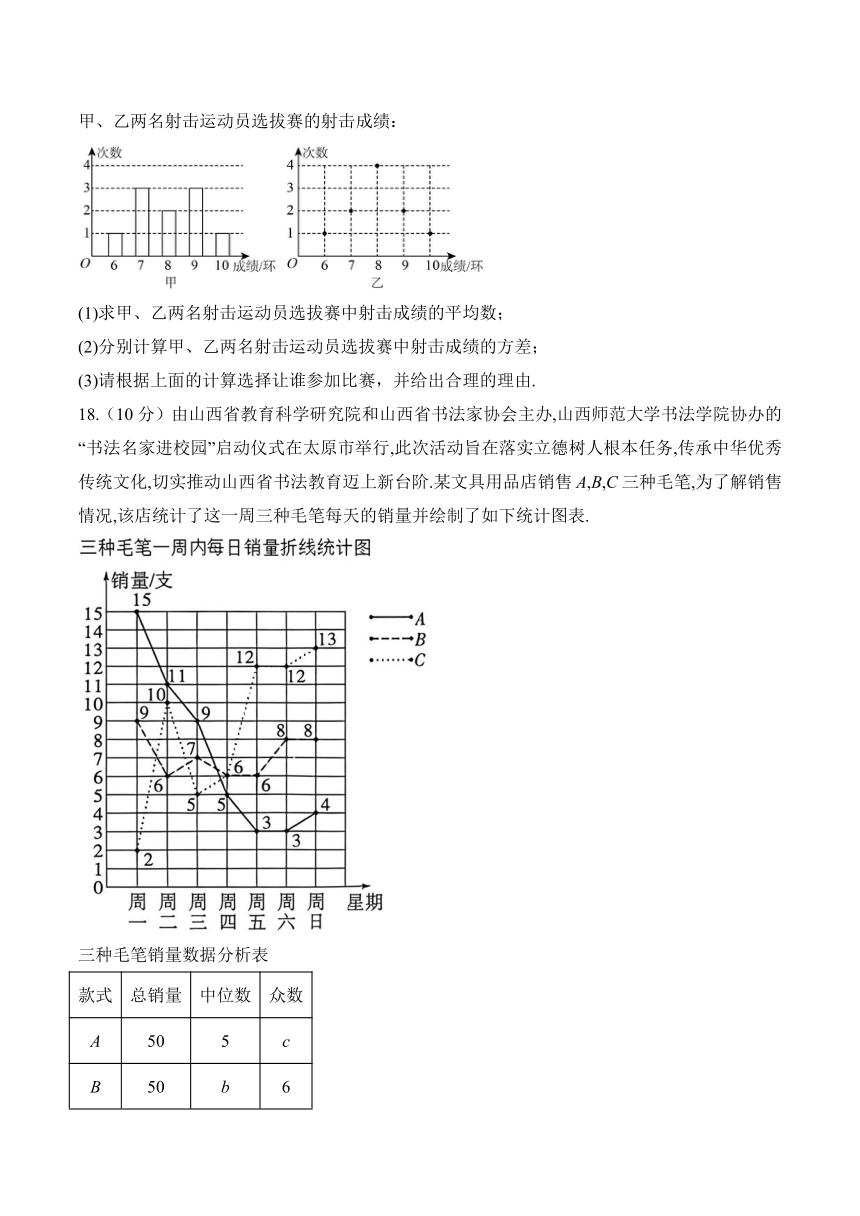
17.(8分)某射击队准备从甲、乙两名射击运动员中选派一名参加比赛,下面两幅图分别表示甲、乙两名射击运动员选拔赛的射击成绩:
(1)求甲、乙两名射击运动员选拔赛中射击成绩的平均数;
(2)分别计算甲、乙两名射击运动员选拔赛中射击成绩的方差;
(3)请根据上面的计算选择让谁参加比赛,并给出合理的理由.
18.(10分)由山西省教育科学研究院和山西省书法家协会主办,山西师范大学书法学院协办的“书法名家进校园”启动仪式在太原市举行,此次活动旨在落实立德树人根本任务,传承中华优秀传统文化,切实推动山西省书法教育迈上新台阶.某文具用品店销售A,B,C三种毛笔,为了解销售情况,该店统计了这一周三种毛笔每天的销量并绘制了如下统计图表.
三种毛笔销量数据分析表
款式 总销量 中位数 众数
A 50 5 c
B 50 b 6
C a 10 12
补充数据:
这三种毛笔每支的利润分别为:A种5元,B种7元,C种4元.
请解答下列问题.
(1)填空:______,______,______;
(2)若后面一周这三种毛笔一共卖出去了240支,请你估计A种毛笔卖出去了多少支;
(3)请你根据以上信息,向该店店主提出一条合理的进货或销售建议.
19.(10分)某班组织开展课外体育活动,在规定时间内,进行定点投篮,对投篮命中数量进行了统计,并制成下面的统计表和如图不完整的折线统计图(不含投篮命中个数为0的数据).
投篮命中数量/个 1 2 3 4 5 6
学生人数 1 2 3 7 6 1
根据以上信息,解决下面的问题:
(1)在本次投篮活动中,投篮命中的学生共有人,并求投篮命中数量的众数和平均数;
(2)补全折线统计图;
(3)嘉淇在统计投篮命中数量的中位数时,把统计表中相邻两个投篮命中的数量m,n错看成了n,m()进行计算,结果错误数据的中位数与原数据的中位数相比发生了改变,求m,n的值.
20.(12分)科教兴国,科普为先,阳光中学组织七、八年级学生参加了“科普赋能,智行未来”科普知识竞赛.现随机抽取了20名学生的竞赛成绩进行整理,描述和分析(成绩用x表示,分为四组:A:,B:,C:,D:),下面给出部分信息.
【数据收集】
七年级20名学生的成绩:68,76,78,79,83,85,86,86,86,86,86,88,88,90,92,92,94,97,100,100,
八年级20名学生的成绩在C组的数据是:83,85,85,86,87,89,89,89,89,
【数据整理、分析】
班级 平均数 中位数 众数
七年级 a 86 86
八年级 87 89
根据以上信息,解答下列问题:
(1)求出a,b的值;
(2)根据以上数据,你认为______年级的学生掌握科普知识较好,请说明理由(写出一条);
(3)该校七年级有500名学生和八年级有480名学生参加了此次科普知识竞赛,若规定成绩90分及以上为优秀,并颁发小奖品.请估计这两个年级参赛学生中获得小奖品的人数.
21.(12分)3月23日是“世界气象日”,为了让同学们了解气象相关知识,某校八年级举办“世界气象日”知识比赛,并从男、女生中各抽取名学生的比赛成绩(比赛成绩为整数,满分分,分及以上为合格).相关数据统计、整理如下:
抽取的15名男生的比赛成绩:,,,,,,,,,,,,,,.
抽取的名女生比赛成绩中位于一组的具体分数:,,,,,.
女生中抽取的学生的比赛成绩频数分布直方图
男、女生抽取的学生的比赛成绩统计表
性别 男生 女生
平均数 76 76
中位数 78 a
众数 b 85
合格率
根据以上信息,解答下列问题:
(1)填空:______,______,并补全频数分布直方图;
(2)根据以上数据分析,请你评价该校八年级男、女生“世界气象日”知识比赛成绩谁更好,并写出理由(一条理由即可);
(3)该校八年级共人,其中女生人,成绩在分及以上为优秀,估计该校八年级学生中“世界气象日”知识比赛成绩优秀的人数.
答案以及解析
1.答案:C
解析:这组数据的平均数是:,
这组数据从小到大排序为:31,32,35,35,37,
一共有5个数据,
中位数为第3位数,即35,
故选:C.
2.答案:D
解析:由表中信息可知,平均数较好的是甲和丙,
又方差越小越稳定,甲和丙中,甲的方差小于丙的方差,所以选甲,
故选:D.
3.答案:B
解析:观察条形统计图可得这些工人日加工零件数的平均数为.
根据中位数的定义,将这32个数据按从小到大的顺序排列,其中第16个、第17个都是6,
∴这些工人日加工零件数的中位数是6.
∵在这32个数据中,6出现了10次,出现的次数最多,
∴这些工人日加工零件数的众数是6.
故选B.
4.答案:D
解析:平均数为:(分);
方差为:;
故选:D.
5.答案:C
解析:根据折线统计图可得:10名选手的成绩分别为80,80,85,90,90,90,90,90,95,95所以最高分为95,众数为90;中位数90;
平均分为.
故选:C.
6.答案:C
解析:由表可知,年龄为14岁与年龄为15岁的频数和为.由频数分布表可知:出现次数最多的是13岁,和中位数出现在13岁年龄段,不会因a、b取不同的值而变化.
故选:C.
7.答案:D
解析:把这组数据从小到大排列为5,6,7,7,8,8,8,处在最中间的数是7,
这组数据的中位数为7,故C不符合题意;
这组数据中8出现了3次,出现的次数最多,
这组数据的众数为8,故B不符合题意;
这组数据的平均数为,故A不符合题意;
这组数据的方差为,故D符合题意;
故选:D
8.答案:C
解析:一组数据,,,的平均数为:,
另一组数据,,,的平均数为:.
故选:C.
9.答案:B
解析:根据题意可得,计算平均数、方差需要全部数据,故A、D不符合题意;
∵,
∴无法确定众数分布在哪一组,故C不符合题意;
从统计图可得:前三组的数据共有,
共有50名学生,中位数为第25与26位的平均数,
∴已知的数据中中位数确定,且不受后面数据的影响,
故选:B.
10.答案:A
解析:A、假设选出的数据没有1,则选出的数据为2,3,5,6时,方差最大,此时,方差为;当数据为1,2,5,6时,,,故该选项符合题意;
B、当该同学选出的四个数字为2,3,5,6时,,,故该选项不符合题意;
C、当该同学选出的四个数字为2,3,4,5时,,故该选项不符合题意;
D、当选出的数据为2,4,5,6或2,3,4,6时,极差也是4,故该选项不符合题意;
故选:A.
11.答案:1
解析:由扇形统计图可得:1分出现的次数最多,所占比例为,
故打分数的众数为1,
故答案为:1.
12.答案:2
解析:一组数据2,3,4,m,的众数为3,
,
这组数的平均数是:,
故这组数的平均数为:2,
故答案为:2.
13.答案:-2
解析:一组数据4,3,2,m,n的众数为3,平均数为2,
,
,,
解得.
故答案为:-2.
14.答案:5
解析:这组数据有唯一众数8,
b为8,
中位数是5,
a是5,
这一组数据的平均数为,
故答案为:5.
15.答案:8
解析:∵一组数据,,,…,的平均数为4,方差为2,
∴,
∴,
则,,,…,的平均数为
则,,,…,的方差为
,
故答案为:8.
16.答案:(1),,
(2)这5名女篮队员的平均身高为
解析:(1)该女子篮球队全队平均身高是,
,
,
.
(2)这5名女篮队员的平均身高为
.
17.答案:(1),
(2)甲的方差:,乙的方差:
(3)选择让乙参赛,理由见解析
解析:(1),
(2)甲的方差:,
乙的方差:
(3)选择让乙参赛.
因为从平均数来看两名运动员的数据相同,从方差来看乙比甲成绩更加稳定.
18.答案:(1)60,7,3
(2)估计A种毛笔卖出去了75支
(3)见解析
解析:(1)根据折线统计图可知,,
由折线统计图,得B种毛笔的销量一共有7个数据,将这7个数据按照从小到大的顺序排列,处于最中间的数据为7,
∴,
A种毛笔销量数据中出现次数最多的数是3,众数是3,即,
故答案为:60,7,3;
(2)(支).
∴估计A种毛笔卖出去了75支;
(3)①由题可得,A、B、C三种毛笔的一周销量相差不大,但B种毛笔的利润最高,因此进货时可适当提高B种毛笔的数量;
②相比后半周,前半周A种毛笔的销量明显很高,
∴销售时要保证A种毛笔在前半周的库存.
19.答案:(1)20,众数为4个,平均数为(个)
(2)图见解析
(3),
解析:(1)投篮命中的学生人数为(人);
众数为4个;
平均数为(个).
故答案为:20;
(2)补全折线统计图如下图:
(3)原投篮命中数量的中位数是;
当1和2互换时,中位数为4,没有变化;
当2和3互换时,中位数为4,没有变化;
当3和4互换时,中位数为,没有变化,此时,;
当4和5互换时,中位数为4,没有变化;
当5和6互换时,中位数为4,没有变化.
∴,.
20.答案:(1)87,88
(2)八;理由见解析
(3)319人
解析:(1)七年级20名学生成绩的平均数(分);
八年级20名学生的成绩在A组中的人数为(人),在B组中的人数为(人),
将八年级20名学生的成绩按照从小到大的顺序排列,排在第10和11位的数为87,89,
∴中位数(分);
(2)理由:七年级和八年级抽取的学生成绩的平均数相同,但八年级的中位数比七年级的中位数大,
故八年级的学生掌握科普知识较好;(合理即可),
故答案为:八;
(3)八年级学生的成绩在D组的人数为(人),
(人),
故估计这两个年级参赛学生中获得小奖品的人数为319人.
21.答案:(1),,图见解析
(2)女生的成绩更优异,理由见解析
(3)
解析:(1)∵总共被抽取女生为15人,被抽取的女生比赛成绩按照从小到大排列后,中位数是第8个女生的比赛成绩,
的人数有,
∴第8个女生的比赛成绩是位于:,,,,,中的,
∴,
∵男生中抽取的学生的比赛成绩为:
,,,,,,,,,,,,,,.
出现次数最多的是,共出现3次,
众数为,
,
故答案为:,
补全补全频数分布直方图如下:
(2)女生的成绩更优异,因为女生的中位数82高于男生的中位数78,所以女生的成绩更优异.
(3)该校八年级共人,其中女生人,则男生有人,
由题意得(人),
答:该校八年级学生中古诗词默写比赛成绩优秀的有人.
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.一组数据:31,32,35,37,35,这组数据的平均数和中位数分别是( )
A.34,34 B.35,35 C.34,35 D.35,34
2.如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲 乙 丙 丁
平均数() 186 182 186 182
方差 3.2 3.2 6.5 6.0
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A.丁 B.丙 C.乙 D.甲
3.如图所示的条形图描述了某车间工人日加工零件数的情况,则这些工人日加工零件数的平均数、中位数、众数分别是( )
A.6.4,10,4 B.6,6,6 C.6.4,6,6 D.6,6,10
4.数学兴趣小组成员小刚对自己的学习质量进行了测试.如图是他最近五次测试成绩(满分为100分)的折线统计图,那么其平均数和方差分别是( )
A.95分, B.96分, C.95分,10 D.96分,10
5.在学校演讲比赛中,10名选手的成绩折线统计图如图所示,则下列说法正确的是( )
A.最高分90 B.众数是5 C.中位数是90 D.平均分为87.5
6.下表是某中学阳光社团40名志愿者的年龄分布统计表.对于a,b取不同的值,下列关于年龄的统计量不会发生改变的是( )
年龄(岁) 12 13 14 15
频数(名) 11 19 a b
A.平均数、众数 B.中位数、平均数
C.众数、中位数 D.平均数、方差
7.某校举行以“我和我的祖国”为主题的演讲比赛,7位评委给某同学打分(满分10分),该同学的得分情况是8,6,8,7,8,5,7.对于该组数据,下列说法错误的是( )
A.平均数为7 B.众数为8 C.中位数为7 D.方差为2
8.已知一组数据,,,的平均数为6,则另一组数据,,,的平均数为( )
A.5 B.6 C.7 D.不确定
9.为了解“睡眠管理”落实情况,某初中学校随机调查50名学生每天平均睡眠时间(时间均保留整数),将样本数据绘制成统计图(如图),其中有两个数据被遮盖关于睡眠时间的统计量中,与被遮盖的数据无关的是( )
A.平均数 B.中位数 C.众数 D.方差
10.小庆、小铁、小娜、小萌四名同学均从1,2,3,4,5,6这六个数字中选出四个数字,玩猜数游戏.下列选项中,能确定该同学选出的四个数字含有1的是( )
A.小庆选出四个数字的方差等于 B.小铁选出四个数字的方差等于
C.小娜选出四个数字的平均数等于 D.小萌选出四个数字的极差等于4
二、填空题(每小题4分,共20分)
11.2024年全国两会提出:以科技创新推动产业创新,以前沿技术催生新产业、新模式、新动力,发展新质生产力,促进高质量发展.某学校数学社团使用问卷星APP发起了“人工智能(AI)知多少?”的问卷调查,把知道的程度由低到高分别记为1分、2分、3分、4分、5分.画出的扇形统计图如图所示,则近打分数的众数为______.
12.已知一组数据2,3,4,m,的众数为3,则平均数为______.
13.已知一组数据:4、3、2、m、n的众数为3,平均数为2,,则n的值为______.
14.已知一组正整数a,1,b,b,3有唯一众数8,中位数是5,则这一组数据的平均数为______.
15.若一组数据,,,…,的平均数为4,方差为2,则,,,…,的方差为__________.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)下表是某女子篮球队其中五名队员的身高情况:(单位:).
女篮队员 A B C D E
个人身高 176 a 207 192 191
个人身高与全队平均身高的差值 b c
(1)求出a,b,c的值;
(2)求该女子篮球队这五名队员的平均身高.
17.(8分)某射击队准备从甲、乙两名射击运动员中选派一名参加比赛,下面两幅图分别表示甲、乙两名射击运动员选拔赛的射击成绩:
(1)求甲、乙两名射击运动员选拔赛中射击成绩的平均数;
(2)分别计算甲、乙两名射击运动员选拔赛中射击成绩的方差;
(3)请根据上面的计算选择让谁参加比赛,并给出合理的理由.
18.(10分)由山西省教育科学研究院和山西省书法家协会主办,山西师范大学书法学院协办的“书法名家进校园”启动仪式在太原市举行,此次活动旨在落实立德树人根本任务,传承中华优秀传统文化,切实推动山西省书法教育迈上新台阶.某文具用品店销售A,B,C三种毛笔,为了解销售情况,该店统计了这一周三种毛笔每天的销量并绘制了如下统计图表.
三种毛笔销量数据分析表
款式 总销量 中位数 众数
A 50 5 c
B 50 b 6
C a 10 12
补充数据:
这三种毛笔每支的利润分别为:A种5元,B种7元,C种4元.
请解答下列问题.
(1)填空:______,______,______;
(2)若后面一周这三种毛笔一共卖出去了240支,请你估计A种毛笔卖出去了多少支;
(3)请你根据以上信息,向该店店主提出一条合理的进货或销售建议.
19.(10分)某班组织开展课外体育活动,在规定时间内,进行定点投篮,对投篮命中数量进行了统计,并制成下面的统计表和如图不完整的折线统计图(不含投篮命中个数为0的数据).
投篮命中数量/个 1 2 3 4 5 6
学生人数 1 2 3 7 6 1
根据以上信息,解决下面的问题:
(1)在本次投篮活动中,投篮命中的学生共有人,并求投篮命中数量的众数和平均数;
(2)补全折线统计图;
(3)嘉淇在统计投篮命中数量的中位数时,把统计表中相邻两个投篮命中的数量m,n错看成了n,m()进行计算,结果错误数据的中位数与原数据的中位数相比发生了改变,求m,n的值.
20.(12分)科教兴国,科普为先,阳光中学组织七、八年级学生参加了“科普赋能,智行未来”科普知识竞赛.现随机抽取了20名学生的竞赛成绩进行整理,描述和分析(成绩用x表示,分为四组:A:,B:,C:,D:),下面给出部分信息.
【数据收集】
七年级20名学生的成绩:68,76,78,79,83,85,86,86,86,86,86,88,88,90,92,92,94,97,100,100,
八年级20名学生的成绩在C组的数据是:83,85,85,86,87,89,89,89,89,
【数据整理、分析】
班级 平均数 中位数 众数
七年级 a 86 86
八年级 87 89
根据以上信息,解答下列问题:
(1)求出a,b的值;
(2)根据以上数据,你认为______年级的学生掌握科普知识较好,请说明理由(写出一条);
(3)该校七年级有500名学生和八年级有480名学生参加了此次科普知识竞赛,若规定成绩90分及以上为优秀,并颁发小奖品.请估计这两个年级参赛学生中获得小奖品的人数.
21.(12分)3月23日是“世界气象日”,为了让同学们了解气象相关知识,某校八年级举办“世界气象日”知识比赛,并从男、女生中各抽取名学生的比赛成绩(比赛成绩为整数,满分分,分及以上为合格).相关数据统计、整理如下:
抽取的15名男生的比赛成绩:,,,,,,,,,,,,,,.
抽取的名女生比赛成绩中位于一组的具体分数:,,,,,.
女生中抽取的学生的比赛成绩频数分布直方图
男、女生抽取的学生的比赛成绩统计表
性别 男生 女生
平均数 76 76
中位数 78 a
众数 b 85
合格率
根据以上信息,解答下列问题:
(1)填空:______,______,并补全频数分布直方图;
(2)根据以上数据分析,请你评价该校八年级男、女生“世界气象日”知识比赛成绩谁更好,并写出理由(一条理由即可);
(3)该校八年级共人,其中女生人,成绩在分及以上为优秀,估计该校八年级学生中“世界气象日”知识比赛成绩优秀的人数.
答案以及解析
1.答案:C
解析:这组数据的平均数是:,
这组数据从小到大排序为:31,32,35,35,37,
一共有5个数据,
中位数为第3位数,即35,
故选:C.
2.答案:D
解析:由表中信息可知,平均数较好的是甲和丙,
又方差越小越稳定,甲和丙中,甲的方差小于丙的方差,所以选甲,
故选:D.
3.答案:B
解析:观察条形统计图可得这些工人日加工零件数的平均数为.
根据中位数的定义,将这32个数据按从小到大的顺序排列,其中第16个、第17个都是6,
∴这些工人日加工零件数的中位数是6.
∵在这32个数据中,6出现了10次,出现的次数最多,
∴这些工人日加工零件数的众数是6.
故选B.
4.答案:D
解析:平均数为:(分);
方差为:;
故选:D.
5.答案:C
解析:根据折线统计图可得:10名选手的成绩分别为80,80,85,90,90,90,90,90,95,95所以最高分为95,众数为90;中位数90;
平均分为.
故选:C.
6.答案:C
解析:由表可知,年龄为14岁与年龄为15岁的频数和为.由频数分布表可知:出现次数最多的是13岁,和中位数出现在13岁年龄段,不会因a、b取不同的值而变化.
故选:C.
7.答案:D
解析:把这组数据从小到大排列为5,6,7,7,8,8,8,处在最中间的数是7,
这组数据的中位数为7,故C不符合题意;
这组数据中8出现了3次,出现的次数最多,
这组数据的众数为8,故B不符合题意;
这组数据的平均数为,故A不符合题意;
这组数据的方差为,故D符合题意;
故选:D
8.答案:C
解析:一组数据,,,的平均数为:,
另一组数据,,,的平均数为:.
故选:C.
9.答案:B
解析:根据题意可得,计算平均数、方差需要全部数据,故A、D不符合题意;
∵,
∴无法确定众数分布在哪一组,故C不符合题意;
从统计图可得:前三组的数据共有,
共有50名学生,中位数为第25与26位的平均数,
∴已知的数据中中位数确定,且不受后面数据的影响,
故选:B.
10.答案:A
解析:A、假设选出的数据没有1,则选出的数据为2,3,5,6时,方差最大,此时,方差为;当数据为1,2,5,6时,,,故该选项符合题意;
B、当该同学选出的四个数字为2,3,5,6时,,,故该选项不符合题意;
C、当该同学选出的四个数字为2,3,4,5时,,故该选项不符合题意;
D、当选出的数据为2,4,5,6或2,3,4,6时,极差也是4,故该选项不符合题意;
故选:A.
11.答案:1
解析:由扇形统计图可得:1分出现的次数最多,所占比例为,
故打分数的众数为1,
故答案为:1.
12.答案:2
解析:一组数据2,3,4,m,的众数为3,
,
这组数的平均数是:,
故这组数的平均数为:2,
故答案为:2.
13.答案:-2
解析:一组数据4,3,2,m,n的众数为3,平均数为2,
,
,,
解得.
故答案为:-2.
14.答案:5
解析:这组数据有唯一众数8,
b为8,
中位数是5,
a是5,
这一组数据的平均数为,
故答案为:5.
15.答案:8
解析:∵一组数据,,,…,的平均数为4,方差为2,
∴,
∴,
则,,,…,的平均数为
则,,,…,的方差为
,
故答案为:8.
16.答案:(1),,
(2)这5名女篮队员的平均身高为
解析:(1)该女子篮球队全队平均身高是,
,
,
.
(2)这5名女篮队员的平均身高为
.
17.答案:(1),
(2)甲的方差:,乙的方差:
(3)选择让乙参赛,理由见解析
解析:(1),
(2)甲的方差:,
乙的方差:
(3)选择让乙参赛.
因为从平均数来看两名运动员的数据相同,从方差来看乙比甲成绩更加稳定.
18.答案:(1)60,7,3
(2)估计A种毛笔卖出去了75支
(3)见解析
解析:(1)根据折线统计图可知,,
由折线统计图,得B种毛笔的销量一共有7个数据,将这7个数据按照从小到大的顺序排列,处于最中间的数据为7,
∴,
A种毛笔销量数据中出现次数最多的数是3,众数是3,即,
故答案为:60,7,3;
(2)(支).
∴估计A种毛笔卖出去了75支;
(3)①由题可得,A、B、C三种毛笔的一周销量相差不大,但B种毛笔的利润最高,因此进货时可适当提高B种毛笔的数量;
②相比后半周,前半周A种毛笔的销量明显很高,
∴销售时要保证A种毛笔在前半周的库存.
19.答案:(1)20,众数为4个,平均数为(个)
(2)图见解析
(3),
解析:(1)投篮命中的学生人数为(人);
众数为4个;
平均数为(个).
故答案为:20;
(2)补全折线统计图如下图:
(3)原投篮命中数量的中位数是;
当1和2互换时,中位数为4,没有变化;
当2和3互换时,中位数为4,没有变化;
当3和4互换时,中位数为,没有变化,此时,;
当4和5互换时,中位数为4,没有变化;
当5和6互换时,中位数为4,没有变化.
∴,.
20.答案:(1)87,88
(2)八;理由见解析
(3)319人
解析:(1)七年级20名学生成绩的平均数(分);
八年级20名学生的成绩在A组中的人数为(人),在B组中的人数为(人),
将八年级20名学生的成绩按照从小到大的顺序排列,排在第10和11位的数为87,89,
∴中位数(分);
(2)理由:七年级和八年级抽取的学生成绩的平均数相同,但八年级的中位数比七年级的中位数大,
故八年级的学生掌握科普知识较好;(合理即可),
故答案为:八;
(3)八年级学生的成绩在D组的人数为(人),
(人),
故估计这两个年级参赛学生中获得小奖品的人数为319人.
21.答案:(1),,图见解析
(2)女生的成绩更优异,理由见解析
(3)
解析:(1)∵总共被抽取女生为15人,被抽取的女生比赛成绩按照从小到大排列后,中位数是第8个女生的比赛成绩,
的人数有,
∴第8个女生的比赛成绩是位于:,,,,,中的,
∴,
∵男生中抽取的学生的比赛成绩为:
,,,,,,,,,,,,,,.
出现次数最多的是,共出现3次,
众数为,
,
故答案为:,
补全补全频数分布直方图如下:
(2)女生的成绩更优异,因为女生的中位数82高于男生的中位数78,所以女生的成绩更优异.
(3)该校八年级共人,其中女生人,则男生有人,
由题意得(人),
答:该校八年级学生中古诗词默写比赛成绩优秀的有人.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
