数学:24.3相似三角形的性质教案(沪科版九年级上)
文档属性
| 名称 | 数学:24.3相似三角形的性质教案(沪科版九年级上) |
|
|
| 格式 | rar | ||
| 文件大小 | 41.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-10-22 15:17:00 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
24.3相似三角形的性质
●学习指导
1.学习了相似三角形的性质后,对于涉及到相似三角形对应角平分线、对应中线、对应高、周长的问题,应立即联想到相似三角形对应线段的比等于相似比,等于周长的比的性质.举例如下.
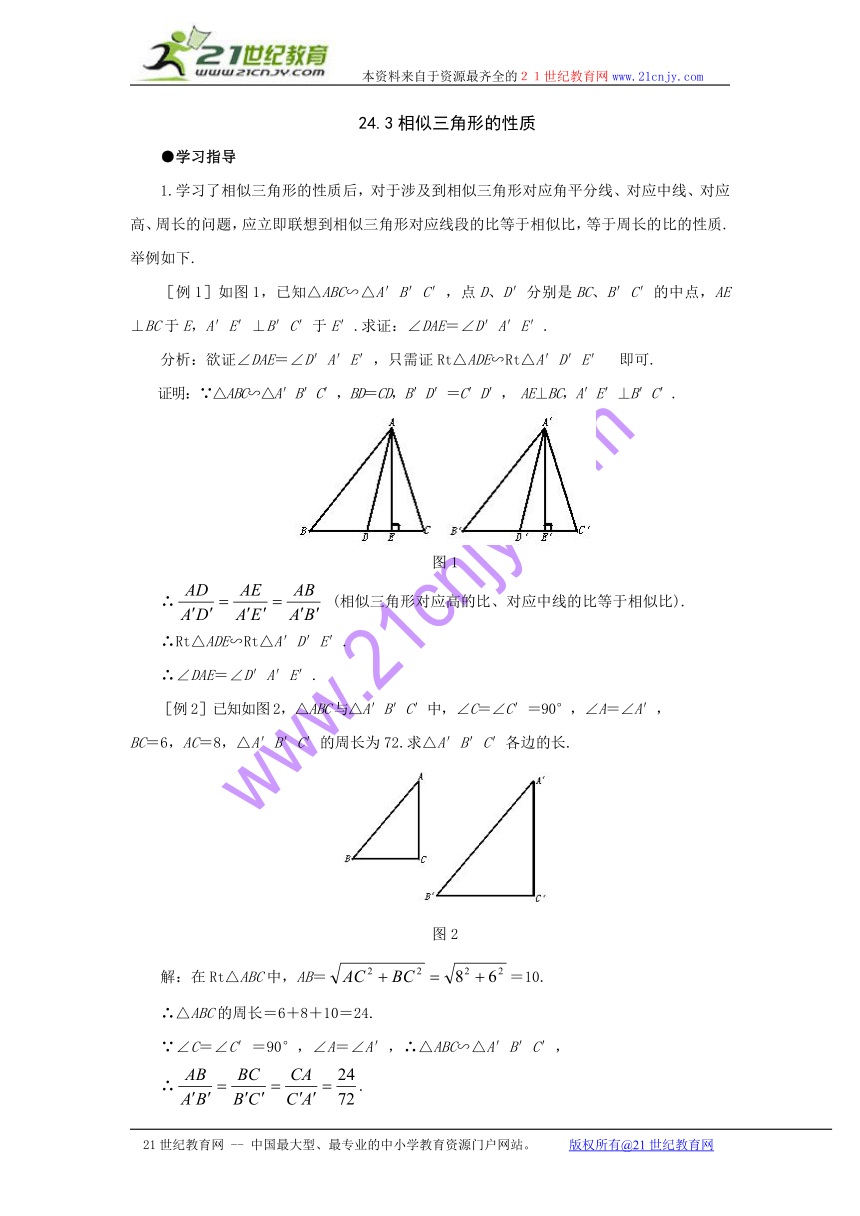
[例1]如图1,已知△ABC∽△A′B′C′,点D、D′分别是BC、B′C′的中点,AE⊥BC于E,A′E′⊥B′C′于E′.求证:∠DAE=∠D′A′E′.
分析:欲证∠DAE=∠D′A′E′,只需证Rt△ADE∽Rt△A′D′E′?即可.?
证明:∵△ABC∽△A′B′C′,BD=CD,B′D′=C′D′, AE⊥BC,A′E′⊥B′C′.
图1
∴ (相似三角形对应高的比、对应中线的比等于相似比).
∴Rt△ADE∽Rt△A′D′E′.
∴∠DAE=∠D′A′E′.
[例2]已知如图2,△ABC与△A′B′C′中,∠C=∠C′=90°,∠A=∠A′,
BC=6,AC=8,△A′B′C′的周长为72.求△A′B′C′各边的长.
图2
解:在Rt△ABC中,AB==10.
∴△ABC的周长=6+8+10=24.
∵∠C=∠C′=90°,∠A=∠A′,∴△ABC∽△A′B′C′,
∴.
即∴A′B′=30, B′C′=18,C′A′=24.
说明:由已知条件知△ABC∽△A′B′C′,已知△ABC各边的长,要求△A′B′C′各边的长,只要求出相似比即可.
[例3]如图3,四边形ABCD中,∠ADC=∠ACB=90°,且AB=18,AC=12,AD=8,CE⊥AB,DF⊥AC,垂足为E、F.
(1)求的值;
(2)求证:CE=CD.
分析:由题设可知,DF、CE分别为△ACD和△ABC的高,
因此只要证得△ACD∽△ABC,根据相似三角形的性质即可求得.
(1) 解:∵AB=18,AC=12,AD=8,
∴
∴.
∵∠AEC=∠AFD=90°,∴Rt△ABC∽Rt△ACD
∵CE⊥AB,DF⊥AC.∴.
(2)证明:∵Rt△ABC∽Rt△ACD,∴∠BAC=∠CAD. 图3
∵CE⊥AB,CD⊥AB,∴CE=CD.
[例4]已知,如图4,△ABC中,OB、OC分别平分∠ABC、∠ACB,OD∥AB交BC于D,OE∥AC交BC于E.求证:BC2=DE(AB+BC+AC)
分析:由OD∥AB,OE∥AC知△ODE∽△ABC,要证结论中有△ABC的周长,从而想到了利用相似三角形的周长比等于相似比证题.
证明:∵OD∥AB
∴∠4=∠ABC,∠1=∠3
又∵∠1=∠2,∴∠2=∠3,∴BD=OD
同理可证:OE=CE
∵OE∥AC,∴∠5=∠ACB,∴△ODE∽△ABC 图4
∴
即
∴BC2=DE(AB+BC+AC)
说明:相似三角形的性质较多,究竟选择哪个性质,需要根据结论的特征灵活选择.
[例5]求证:相似三角形的面积比等于相似比的平方.
已知:如图5,△ABC∽△A′B′C,′△ABC与△A′B′C′的相似比为k.
求证:=k2
图5
分析:根据三角形的面积公式“三角形面积等于三角形的一边乘以这边上的高的一半”可先作出BC和B′C′边上的高,再根据相似三角形对应高的比,对应边的比都等于相似比即可证出.
证明:分别过A、A′作BC、B′C′的垂线,垂足分别为D、D′.
∵△ABC∽△A′B′C′
∴=k(相似三角形对应边的比、对应高的比等于相似比)
∴
说明:此结论在原教材中是定理,现已删去,对此结论在解决填空题和选择题中可直接应用.但在求解题中要写出推导过程.
[例6]如图6,正方形ABCD中,E为AB的中点,F为CD延长线上一点,且∠FEC=∠FCE,EF交AD于F.
求证:S△AEP=4S△PDF.
分析:△AEP∽△PDF易证,要证出S△AEP=4S△PDF,关键证其相似比为2∶1. 图6
证明:过F作FG⊥CE与G,则CG=CE
∵四边形ABCD是正方形
∴AB∥CD,AB=BC=CD,∠B=90°
∴∠BEC=∠FCE,∠B=∠FGC=90°
∴△BCE∽△GFC∴
设AE=BE=x,则BC=CD=AB=2x
CE=
∴
∴DF=∵AB∥CD,∴△AEP∽△DFP,∴
∴=4,∴S△AEP=4S△DFP
说明:有等腰三角形时,常作底边上的高构造三线合一的基本图形,另外该题还可延长AB至N,使BN=BE,边结CN,再证△CEN∽△FEC,请读者自己完成.
2.利用相似三角形的性质还可解决许多实际问题,举例如下.
[例7]如图7,有一批形状大小相同的不锈钢片,呈直角三角形,已知∠C=90°,AC=12 cm,BC=5 cm,试设计一种方案,用这批不锈钢片裁出面积最大的正方形不锈钢片,并求出这种不锈钢片的边长.
分析:要求面积最大的正方形,则正方形的顶点应落在△ABC的边上,那么顶点落在边上时有如图8、9两种情况.
图7 图 8 图9
解:如图8,设正方形EFGH的边长为xcm,过C作CD⊥AB于D,交EH于点M.
∵∠ACB=90°,AC=12,BC=5,∴AB=.
∵AB·CD=AC·BC,∴CD=.
∵EH∥AB,∴△CEH∽△CAB.∴.
即 (cm).
如图9,设正方形CFGH的边长为ycm.
∵GH∥AC,∴ (cm).
∵x<y,∴应按图9裁剪,这时正方形面积最大,它的边长为cm.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
24.3相似三角形的性质
●学习指导
1.学习了相似三角形的性质后,对于涉及到相似三角形对应角平分线、对应中线、对应高、周长的问题,应立即联想到相似三角形对应线段的比等于相似比,等于周长的比的性质.举例如下.
[例1]如图1,已知△ABC∽△A′B′C′,点D、D′分别是BC、B′C′的中点,AE⊥BC于E,A′E′⊥B′C′于E′.求证:∠DAE=∠D′A′E′.
分析:欲证∠DAE=∠D′A′E′,只需证Rt△ADE∽Rt△A′D′E′?即可.?
证明:∵△ABC∽△A′B′C′,BD=CD,B′D′=C′D′, AE⊥BC,A′E′⊥B′C′.
图1
∴ (相似三角形对应高的比、对应中线的比等于相似比).
∴Rt△ADE∽Rt△A′D′E′.
∴∠DAE=∠D′A′E′.
[例2]已知如图2,△ABC与△A′B′C′中,∠C=∠C′=90°,∠A=∠A′,
BC=6,AC=8,△A′B′C′的周长为72.求△A′B′C′各边的长.
图2
解:在Rt△ABC中,AB==10.
∴△ABC的周长=6+8+10=24.
∵∠C=∠C′=90°,∠A=∠A′,∴△ABC∽△A′B′C′,
∴.
即∴A′B′=30, B′C′=18,C′A′=24.
说明:由已知条件知△ABC∽△A′B′C′,已知△ABC各边的长,要求△A′B′C′各边的长,只要求出相似比即可.
[例3]如图3,四边形ABCD中,∠ADC=∠ACB=90°,且AB=18,AC=12,AD=8,CE⊥AB,DF⊥AC,垂足为E、F.
(1)求的值;
(2)求证:CE=CD.
分析:由题设可知,DF、CE分别为△ACD和△ABC的高,
因此只要证得△ACD∽△ABC,根据相似三角形的性质即可求得.
(1) 解:∵AB=18,AC=12,AD=8,
∴
∴.
∵∠AEC=∠AFD=90°,∴Rt△ABC∽Rt△ACD
∵CE⊥AB,DF⊥AC.∴.
(2)证明:∵Rt△ABC∽Rt△ACD,∴∠BAC=∠CAD. 图3
∵CE⊥AB,CD⊥AB,∴CE=CD.
[例4]已知,如图4,△ABC中,OB、OC分别平分∠ABC、∠ACB,OD∥AB交BC于D,OE∥AC交BC于E.求证:BC2=DE(AB+BC+AC)
分析:由OD∥AB,OE∥AC知△ODE∽△ABC,要证结论中有△ABC的周长,从而想到了利用相似三角形的周长比等于相似比证题.
证明:∵OD∥AB
∴∠4=∠ABC,∠1=∠3
又∵∠1=∠2,∴∠2=∠3,∴BD=OD
同理可证:OE=CE
∵OE∥AC,∴∠5=∠ACB,∴△ODE∽△ABC 图4
∴
即
∴BC2=DE(AB+BC+AC)
说明:相似三角形的性质较多,究竟选择哪个性质,需要根据结论的特征灵活选择.
[例5]求证:相似三角形的面积比等于相似比的平方.
已知:如图5,△ABC∽△A′B′C,′△ABC与△A′B′C′的相似比为k.
求证:=k2
图5
分析:根据三角形的面积公式“三角形面积等于三角形的一边乘以这边上的高的一半”可先作出BC和B′C′边上的高,再根据相似三角形对应高的比,对应边的比都等于相似比即可证出.
证明:分别过A、A′作BC、B′C′的垂线,垂足分别为D、D′.
∵△ABC∽△A′B′C′
∴=k(相似三角形对应边的比、对应高的比等于相似比)
∴
说明:此结论在原教材中是定理,现已删去,对此结论在解决填空题和选择题中可直接应用.但在求解题中要写出推导过程.
[例6]如图6,正方形ABCD中,E为AB的中点,F为CD延长线上一点,且∠FEC=∠FCE,EF交AD于F.
求证:S△AEP=4S△PDF.
分析:△AEP∽△PDF易证,要证出S△AEP=4S△PDF,关键证其相似比为2∶1. 图6
证明:过F作FG⊥CE与G,则CG=CE
∵四边形ABCD是正方形
∴AB∥CD,AB=BC=CD,∠B=90°
∴∠BEC=∠FCE,∠B=∠FGC=90°
∴△BCE∽△GFC∴
设AE=BE=x,则BC=CD=AB=2x
CE=
∴
∴DF=∵AB∥CD,∴△AEP∽△DFP,∴
∴=4,∴S△AEP=4S△DFP
说明:有等腰三角形时,常作底边上的高构造三线合一的基本图形,另外该题还可延长AB至N,使BN=BE,边结CN,再证△CEN∽△FEC,请读者自己完成.
2.利用相似三角形的性质还可解决许多实际问题,举例如下.
[例7]如图7,有一批形状大小相同的不锈钢片,呈直角三角形,已知∠C=90°,AC=12 cm,BC=5 cm,试设计一种方案,用这批不锈钢片裁出面积最大的正方形不锈钢片,并求出这种不锈钢片的边长.
分析:要求面积最大的正方形,则正方形的顶点应落在△ABC的边上,那么顶点落在边上时有如图8、9两种情况.
图7 图 8 图9
解:如图8,设正方形EFGH的边长为xcm,过C作CD⊥AB于D,交EH于点M.
∵∠ACB=90°,AC=12,BC=5,∴AB=.
∵AB·CD=AC·BC,∴CD=.
∵EH∥AB,∴△CEH∽△CAB.∴.
即 (cm).
如图9,设正方形CFGH的边长为ycm.
∵GH∥AC,∴ (cm).
∵x<y,∴应按图9裁剪,这时正方形面积最大,它的边长为cm.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
