北师大版数学八年级上册5.7用二元一次方程组确定一次函数表达式 同步练习(含答案)
文档属性
| 名称 | 北师大版数学八年级上册5.7用二元一次方程组确定一次函数表达式 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 79.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-20 16:18:49 | ||
图片预览



文档简介
课 时 练
第5单元 二元一次方程组
用二元一次方程组确定一次函数表达式
一、选择题(共5小题)
1. 下列各选项中,一次函数图象的交点是方程组 的解的是
A. 和 B. 和
C. 和 D. 和
2. 在平面直角坐标系中,点 在直线 上,则 的值是
A. B. C. D.
3. 如图所示,过点 的一次函数的图象与正比例函数 的图象相交于点 ,能表示这个一次函数图象的方程是
A. B. C. D.
4. 若三条直线 ,, 相交于同一点,则 的值为
A. B. C. D. 无法确定
5. 点 在直线 和直线 上,且 , 均为正整数,则 的值为
A. B. C. D.
二、填空题(共6小题)
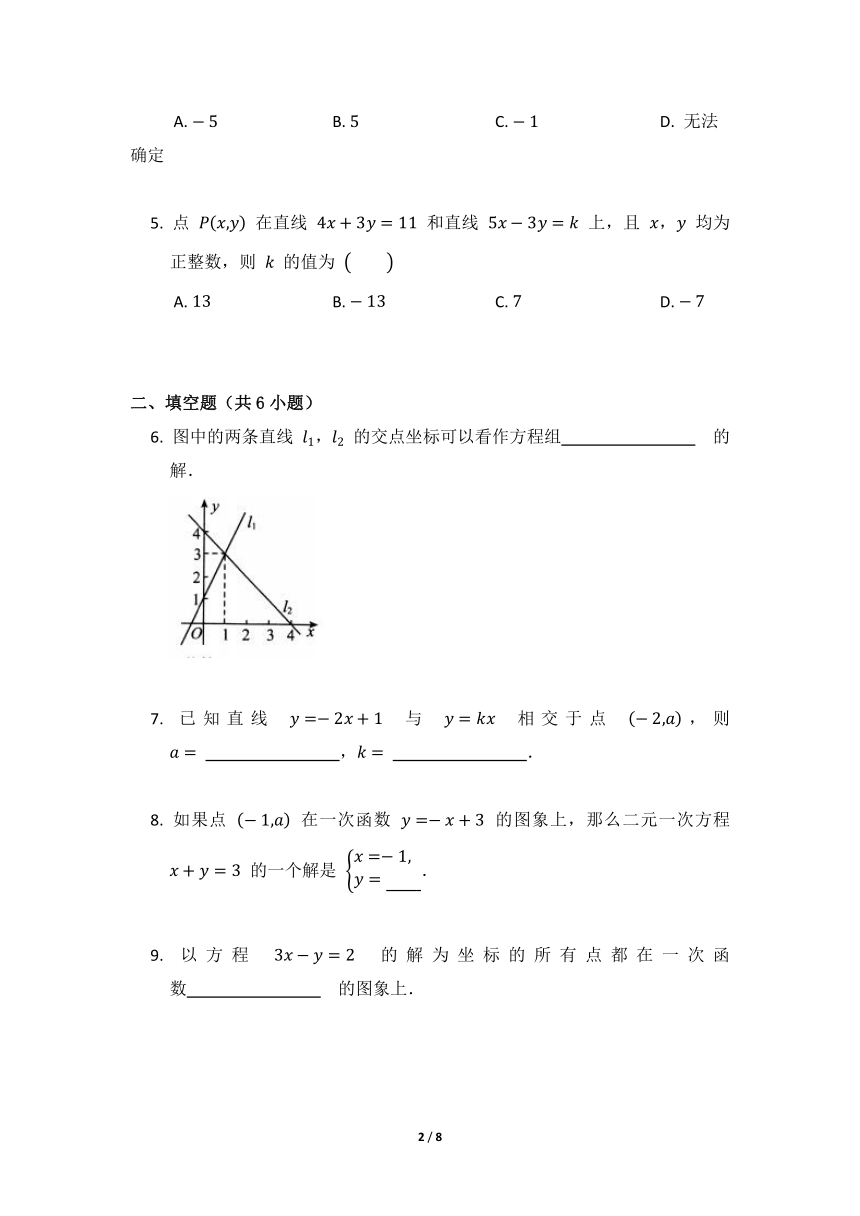
6. 图中的两条直线 , 的交点坐标可以看作方程组 的解.
7. 已知直线 与 相交于点 ,则 , .
8. 如果点 在一次函数 的图象上,那么二元一次方程 的一个解是 .
9. 以方程 的解为坐标的所有点都在一次函数 的图象上.
10. 是关于 , 的方程 的一个解,且 ,则 .
11. 函数 的图象与函数 的图象的交点坐标为 .
三、解答题(共6小题)
12. 某市自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法.若某户居民应交水费 (元)与用水量 (吨)的函数关系如图所示.
(1)分别写出当 和 时, 与 的函数关系式;
(2)某用户10月份用水量为 吨,则应交水费多少元 若该用户11月份交了 元的水费,则他该月用水多少吨
13. 在弹性限度内,弹簧的长度 (厘米)是所挂物体质量 (千克)的一次函数.当所挂物体的质量为 千克时,弹簧长 厘米;当所挂物体的质量为 千克时,弹簧长 厘米.写出 与 之间的函数关系式,并求当所挂物体的质量为 千克时弹簧的长度.
14. 如图所示,, 都是一次函数的图象,且相交于点 .你认为点 的坐标可以看作是怎样的二元一次方程组的解呢 求出点 的坐标.
15. 一次函数 表示的直线经过点 ,,试判断点 是否在直线 上.
16. 某乡镇决定对 , 两村之间的公路进行改造,并由甲工程队从 村向 村方向修筑,乙工程队从 村向 村方向修筑.已知甲工程队先施工 天,乙工程队再开始施工.乙工程队施工几天后,因另有任务提前离开,余下的任务由甲工程队单独完成,直到公路修通.甲、乙两个工程队修公路的长度 (米)与施工时间 (天)之间的函数图象如图所示.
(1)乙工程队每天修公路多少米
(2)分别求甲、乙工程队修公路的长度 (米)与施工时间 (天)之间的函数关系式.
(3)若该项工程由甲、乙两工程队一直合作施工,需几天完成
17. 某电力公司制定了新的用电收费标准,每月用电量 (度)与应付电费 (元)的关系如图所示.
(1)根据图象,请分别求出当 和 时, 与 的函数关系式.
(2)当每月用电量不超过 度时,收费标准是 ;当每月用电量超过 度时,收费标准是 .
答案
1. B
2. A
3. D
4. C
5. C
6.
7. ,
8.
9.
10.
11.
12. (1) 当 时,
设函数解析式为 .代入点 得 .
;
当 时,
设函数解析式为 .代入点 ,,
得 ,,
.
(2) 元,
某用户10月份用水量为 吨,则应交水费 元.
,
得 ,
若该用户11月份交了 元的水费,则他该月用水 吨.
13. 设函数解析式为 ,
代入点 ,,
解得 ,,
.
当 时,.
14. 由图得知, 的解析式为 .
的解析式为 .
点 的坐标可以看作是方程组
解方程组得
点 的坐标为 .
15. 把点 , 代入一次函数 ,
解得 ,,
一次函数解析式为 ,
点 在直线 上.
16. (1) 乙工程队每天修公路 米.
(2) 设乙工程队修公路的长度 (米)与施工时间 (天)之间的函数关系式为 ,
代入点 ,
解得 ,,
.
当 时,.
设甲工程队修公路的长度 (米)与施工时间 (天)之间的函数关系式为 ,
代入点 ,
解得 ,
.
(3) 当 时,,
该公路总长为 (米).
设需 天完成,
由题意得
解得
答:该项工程由甲、乙两工程队一直合作施工,需 天完成.
17. (1) 当 时,
设 ,当 时, ,
得 ,
,
当 时,
设 ,当 时,, 时, ,
得 ,,
.
(2) 元/度;其中的50度每度 元,超过部分每度 元/度.
8 / 8
第5单元 二元一次方程组
用二元一次方程组确定一次函数表达式
一、选择题(共5小题)
1. 下列各选项中,一次函数图象的交点是方程组 的解的是
A. 和 B. 和
C. 和 D. 和
2. 在平面直角坐标系中,点 在直线 上,则 的值是
A. B. C. D.
3. 如图所示,过点 的一次函数的图象与正比例函数 的图象相交于点 ,能表示这个一次函数图象的方程是
A. B. C. D.
4. 若三条直线 ,, 相交于同一点,则 的值为
A. B. C. D. 无法确定
5. 点 在直线 和直线 上,且 , 均为正整数,则 的值为
A. B. C. D.
二、填空题(共6小题)
6. 图中的两条直线 , 的交点坐标可以看作方程组 的解.
7. 已知直线 与 相交于点 ,则 , .
8. 如果点 在一次函数 的图象上,那么二元一次方程 的一个解是 .
9. 以方程 的解为坐标的所有点都在一次函数 的图象上.
10. 是关于 , 的方程 的一个解,且 ,则 .
11. 函数 的图象与函数 的图象的交点坐标为 .
三、解答题(共6小题)
12. 某市自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法.若某户居民应交水费 (元)与用水量 (吨)的函数关系如图所示.
(1)分别写出当 和 时, 与 的函数关系式;
(2)某用户10月份用水量为 吨,则应交水费多少元 若该用户11月份交了 元的水费,则他该月用水多少吨
13. 在弹性限度内,弹簧的长度 (厘米)是所挂物体质量 (千克)的一次函数.当所挂物体的质量为 千克时,弹簧长 厘米;当所挂物体的质量为 千克时,弹簧长 厘米.写出 与 之间的函数关系式,并求当所挂物体的质量为 千克时弹簧的长度.
14. 如图所示,, 都是一次函数的图象,且相交于点 .你认为点 的坐标可以看作是怎样的二元一次方程组的解呢 求出点 的坐标.
15. 一次函数 表示的直线经过点 ,,试判断点 是否在直线 上.
16. 某乡镇决定对 , 两村之间的公路进行改造,并由甲工程队从 村向 村方向修筑,乙工程队从 村向 村方向修筑.已知甲工程队先施工 天,乙工程队再开始施工.乙工程队施工几天后,因另有任务提前离开,余下的任务由甲工程队单独完成,直到公路修通.甲、乙两个工程队修公路的长度 (米)与施工时间 (天)之间的函数图象如图所示.
(1)乙工程队每天修公路多少米
(2)分别求甲、乙工程队修公路的长度 (米)与施工时间 (天)之间的函数关系式.
(3)若该项工程由甲、乙两工程队一直合作施工,需几天完成
17. 某电力公司制定了新的用电收费标准,每月用电量 (度)与应付电费 (元)的关系如图所示.
(1)根据图象,请分别求出当 和 时, 与 的函数关系式.
(2)当每月用电量不超过 度时,收费标准是 ;当每月用电量超过 度时,收费标准是 .
答案
1. B
2. A
3. D
4. C
5. C
6.
7. ,
8.
9.
10.
11.
12. (1) 当 时,
设函数解析式为 .代入点 得 .
;
当 时,
设函数解析式为 .代入点 ,,
得 ,,
.
(2) 元,
某用户10月份用水量为 吨,则应交水费 元.
,
得 ,
若该用户11月份交了 元的水费,则他该月用水 吨.
13. 设函数解析式为 ,
代入点 ,,
解得 ,,
.
当 时,.
14. 由图得知, 的解析式为 .
的解析式为 .
点 的坐标可以看作是方程组
解方程组得
点 的坐标为 .
15. 把点 , 代入一次函数 ,
解得 ,,
一次函数解析式为 ,
点 在直线 上.
16. (1) 乙工程队每天修公路 米.
(2) 设乙工程队修公路的长度 (米)与施工时间 (天)之间的函数关系式为 ,
代入点 ,
解得 ,,
.
当 时,.
设甲工程队修公路的长度 (米)与施工时间 (天)之间的函数关系式为 ,
代入点 ,
解得 ,
.
(3) 当 时,,
该公路总长为 (米).
设需 天完成,
由题意得
解得
答:该项工程由甲、乙两工程队一直合作施工,需 天完成.
17. (1) 当 时,
设 ,当 时, ,
得 ,
,
当 时,
设 ,当 时,, 时, ,
得 ,,
.
(2) 元/度;其中的50度每度 元,超过部分每度 元/度.
8 / 8
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
