21.3二次函数与一元二次方程第1课时 课件(共17张PPT)024—2025学年数学九年级上册(沪科版)
文档属性
| 名称 | 21.3二次函数与一元二次方程第1课时 课件(共17张PPT)024—2025学年数学九年级上册(沪科版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 804.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-19 22:07:20 | ||
图片预览


文档简介
(共17张PPT)
21.3 二次函数与一元二次方程
第 1 课时
学习目标
二次函数与一元二次方程
准备好了吗?一起去探索吧!
1.理解二次函数图象与x轴交点的横坐标与一元二次方程的根之间的联系.
2.经历探索二次函数与一元二次方程的关系的过程,渗透数形结合的思想方法.
3.通过共同探究的方式,培养学生的合作交流意识,以及观察问题和解决问题的能力.
4.在探索二次函数与一元二次方程的关系的过程中,让学生感受数学知识之间的内在联系,认识到事物之间的联系与转化.
回顾与思考
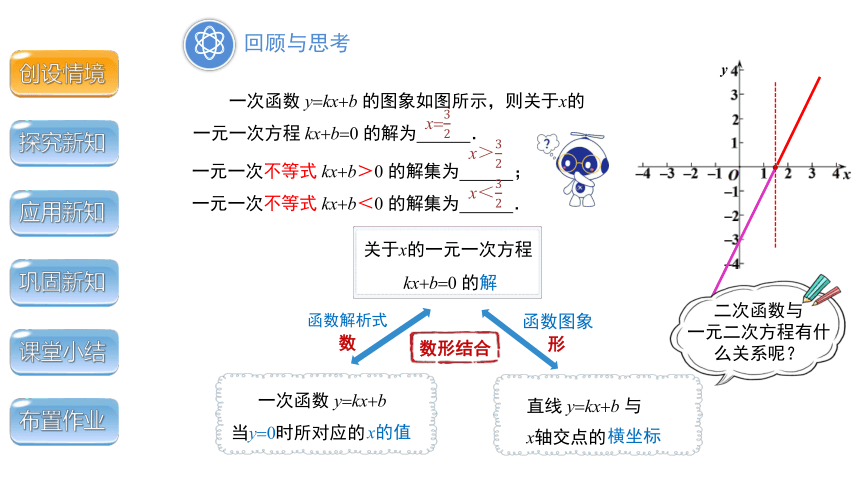
一次函数 y kx b 的图象如图所示,则关于x的一元一次方程 kx b 0 的解为 .
x
关于x的一元一次方程
kx b 0 的解
一次函数 y kx b
当y 0时所对应的
直线 y kx b 与
x轴交点的
函数解析式
函数图象
数
形
数形结合
y
x的值
横坐标
一元一次不等式 kx b>0 的解集为 ;
一元一次不等式 kx b<0 的解集为 .
x>
x<
二次函数与
一元二次方程有什么关系呢?
观察
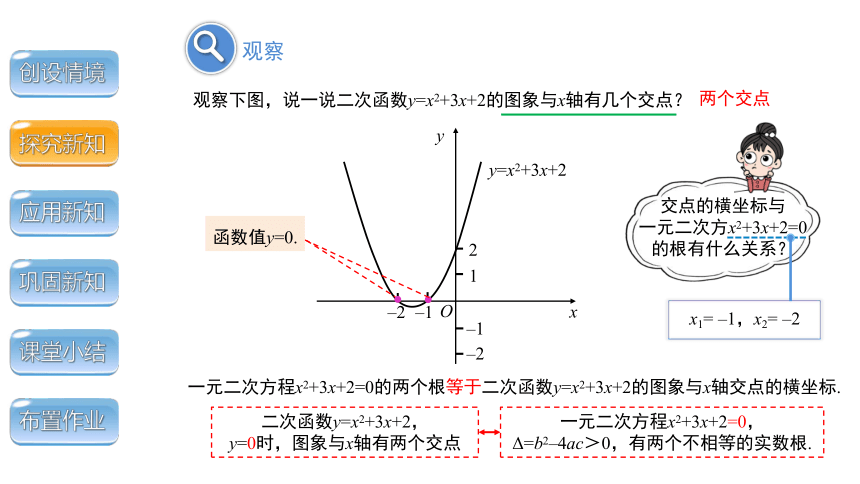
观察下图,说一说二次函数y=x2+3x+2的图象与x轴有几个交点?
y
x
O
–2
–1
2
1
y=x2+3x+2
交点的横坐标与
一元二次方x2+3x+2=0的根有什么关系?
两个交点
x1= –1,x2= –2
函数值y=0.
一元二次方程x2+3x+2=0的两个根等于二次函数y=x2+3x+2的图象与x轴交点的横坐标.
一元二次方程x2+3x+2=0,
Δ=b2–4ac>0,有两个不相等的实数根.
二次函数y=x2+3x+2,
y=0时,图象与x轴有两个交点
–1
–2
观察
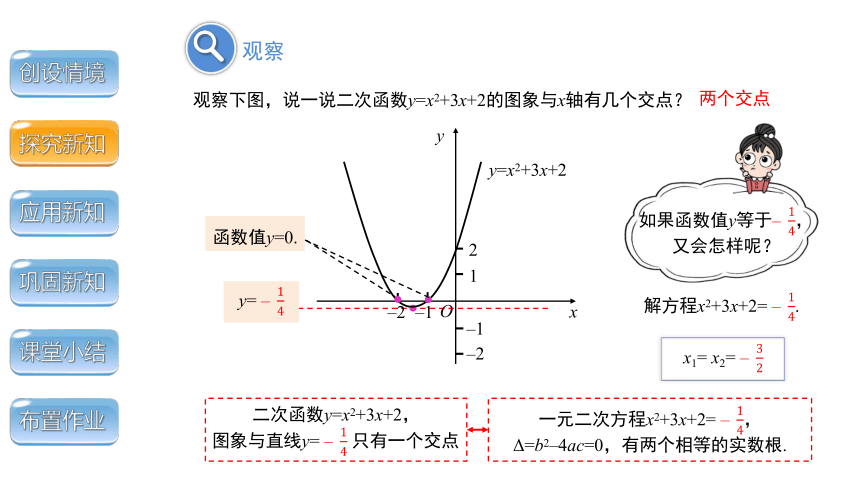
观察下图,说一说二次函数y=x2+3x+2的图象与x轴有几个交点?
如果函数值y等于–,
又会怎样呢?
两个交点
y= –
解方程x2+3x+2= –.
x1= x2= –
一元二次方程x2+3x+2= –,
Δ=b2–4ac=0,有两个相等的实数根.
二次函数y=x2+3x+2,
图象与直线y= – 只有一个交点
x
O
–2
–1
2
1
y=x2+3x+2
函数值y=0.
–1
–2
y
观察
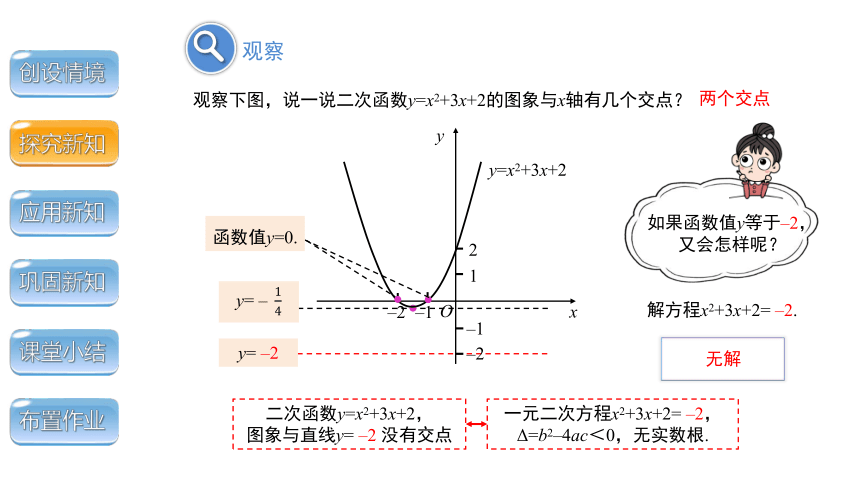
观察下图,说一说二次函数y=x2+3x+2的图象与x轴有几个交点?
如果函数值y等于–2,
又会怎样呢?
两个交点
解方程x2+3x+2= –2.
无解
一元二次方程x2+3x+2= –2,
Δ=b2–4ac<0,无实数根.
二次函数y=x2+3x+2,
图象与直线y= –2 没有交点
y= –
x
O
–2
–1
2
1
y=x2+3x+2
函数值y=0.
–1
–2
y= –2
y
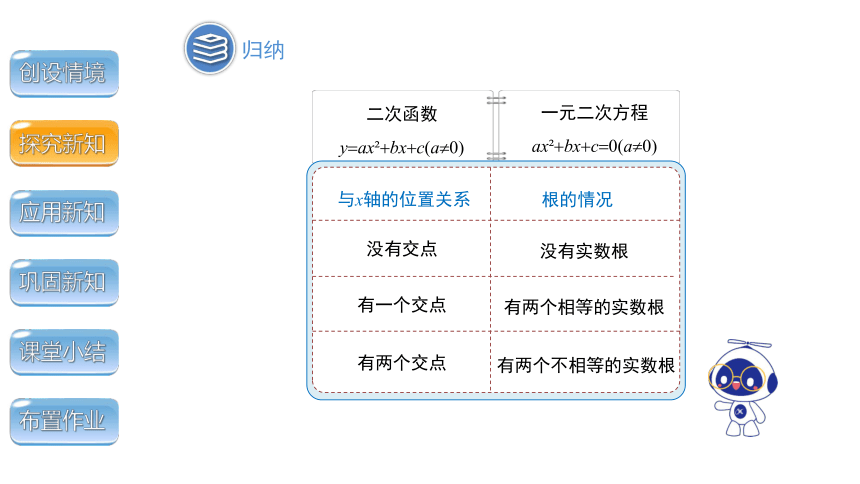
归纳
二次函数
y ax bx c(a 0)
一元二次方程
ax bx c 0(a 0)
与x轴的位置关系
根的情况
没有交点
没有实数根
有一个交点
有两个相等的实数根
有两个交点
有两个不相等的实数根
画出下列二次函数的图象,能否写出相应的一元二次方程的根?
2,1
3
没有实数根
(1)y x2 x 2 (2)y x2 6x 9 (3)y x2 x 1
做一做
典型例题
如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线将是一条抛物线,如果不考虑空气阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系 h 20t 5t 2.
(1)球的飞行高度能否达到15m?如能,需要多少飞行时间?
(2)球的飞行高度能否达到 20 m 若能,需要多少时间
(3)球的飞行高度能否达到 20.5 m 为什么?
(4)球从飞出到落地要用多少时间
典型例题
如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线将是一条抛物线,如果不考虑空气阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系 h 20t 5t 2.
(1)球的飞行高度能否达到15m?如能,需要多少飞行时间?
解:(1)当 h 15 时,
20t 5t2 15
t2 4t 3 0
t1 1,t2 3
当球飞行 1s 和 3s 时,它的高度为15m .
1s
3s
15 m
能否结合图象说明?
典型例题
如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线将是一条抛物线,如果不考虑空气阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系 h 20t 5t 2.
(2)球的飞行高度能否达到 20 m 若能,需要多少时间
(2)当 h 20 时,
20t 5t2 20
t2 4t 4 0
t1 t2 2
2s
20 m
当球飞行 2s 时,它的高度为 20m .
典型例题
如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线将是一条抛物线,如果不考虑空气阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系 h 20t 5t 2.
(3)球的飞行高度能否达到 20.5 m 为什么?
(3)当 h 20.5 时,
20t 5t2 20.5
t2 4t 4.1 0
∵( 4)2 4×4.1<0 ,∴方程无实根.
∴球的飞行高度达不到20.5m.
20.5 m
典型例题
如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线将是一条抛物线,如果不考虑空气阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系 h 20t 5t 2.
(4)球从飞出到落地要用多少时间
20t 5t2 0
t 2 4t 0
t1 0,t2 4
当球飞行 0s 和 4s 时,它的高度为 0m ,即 0s时,球从地面飞出,4s 时球落回地面.
(4)当 h 0 时,
小球从飞出到落地要用4s.
0s
4s
0 m
抢答
随堂练习
1.二次函数y x2 2x 1的图象与x轴的交点个数是( )
A.0 B.1 C.2 D.3
2.不与x轴相交的抛物线是( )
A. y 2x2 3 B. y 2x2 3
C. y x2 3x D. y 2(x 1)2 3
3.抛物线y ax2 bx c与x轴的交点坐标为(1,0),(3,0),则方程ax2 bx c 0的解为____________ .
B
x1 1,x2 3
D
抢答
随堂练习
4. 二次函数y ax2 bx c的图象如下图所示,则ax2 bx c 0的解为 ,
ax2 bx c>0的解为 .
x1 1,x2 3
x< 1或x>3
二次函数与一元二次方程
二次函数与一元二次方程的关联:
结合“数、形”解释二次函数与一元二次方程的关系:
没有交点
没有实数根
有一个交点
有两个相等的实数根
有两个交点
有两个不相等的实数根
y ax bx c(a 0)
与x轴的位置关系
ax bx c 0 (a≠0)
根的情况
数
形
二次函数
y ax bx c(a 0)
一元二次方程
ax bx c m(a 0)
y为定值m
教科书第33页练习
第1、2、3题
21.3 二次函数与一元二次方程
第 1 课时
学习目标
二次函数与一元二次方程
准备好了吗?一起去探索吧!
1.理解二次函数图象与x轴交点的横坐标与一元二次方程的根之间的联系.
2.经历探索二次函数与一元二次方程的关系的过程,渗透数形结合的思想方法.
3.通过共同探究的方式,培养学生的合作交流意识,以及观察问题和解决问题的能力.
4.在探索二次函数与一元二次方程的关系的过程中,让学生感受数学知识之间的内在联系,认识到事物之间的联系与转化.
回顾与思考
一次函数 y kx b 的图象如图所示,则关于x的一元一次方程 kx b 0 的解为 .
x
关于x的一元一次方程
kx b 0 的解
一次函数 y kx b
当y 0时所对应的
直线 y kx b 与
x轴交点的
函数解析式
函数图象
数
形
数形结合
y
x的值
横坐标
一元一次不等式 kx b>0 的解集为 ;
一元一次不等式 kx b<0 的解集为 .
x>
x<
二次函数与
一元二次方程有什么关系呢?
观察
观察下图,说一说二次函数y=x2+3x+2的图象与x轴有几个交点?
y
x
O
–2
–1
2
1
y=x2+3x+2
交点的横坐标与
一元二次方x2+3x+2=0的根有什么关系?
两个交点
x1= –1,x2= –2
函数值y=0.
一元二次方程x2+3x+2=0的两个根等于二次函数y=x2+3x+2的图象与x轴交点的横坐标.
一元二次方程x2+3x+2=0,
Δ=b2–4ac>0,有两个不相等的实数根.
二次函数y=x2+3x+2,
y=0时,图象与x轴有两个交点
–1
–2
观察
观察下图,说一说二次函数y=x2+3x+2的图象与x轴有几个交点?
如果函数值y等于–,
又会怎样呢?
两个交点
y= –
解方程x2+3x+2= –.
x1= x2= –
一元二次方程x2+3x+2= –,
Δ=b2–4ac=0,有两个相等的实数根.
二次函数y=x2+3x+2,
图象与直线y= – 只有一个交点
x
O
–2
–1
2
1
y=x2+3x+2
函数值y=0.
–1
–2
y
观察
观察下图,说一说二次函数y=x2+3x+2的图象与x轴有几个交点?
如果函数值y等于–2,
又会怎样呢?
两个交点
解方程x2+3x+2= –2.
无解
一元二次方程x2+3x+2= –2,
Δ=b2–4ac<0,无实数根.
二次函数y=x2+3x+2,
图象与直线y= –2 没有交点
y= –
x
O
–2
–1
2
1
y=x2+3x+2
函数值y=0.
–1
–2
y= –2
y
归纳
二次函数
y ax bx c(a 0)
一元二次方程
ax bx c 0(a 0)
与x轴的位置关系
根的情况
没有交点
没有实数根
有一个交点
有两个相等的实数根
有两个交点
有两个不相等的实数根
画出下列二次函数的图象,能否写出相应的一元二次方程的根?
2,1
3
没有实数根
(1)y x2 x 2 (2)y x2 6x 9 (3)y x2 x 1
做一做
典型例题
如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线将是一条抛物线,如果不考虑空气阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系 h 20t 5t 2.
(1)球的飞行高度能否达到15m?如能,需要多少飞行时间?
(2)球的飞行高度能否达到 20 m 若能,需要多少时间
(3)球的飞行高度能否达到 20.5 m 为什么?
(4)球从飞出到落地要用多少时间
典型例题
如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线将是一条抛物线,如果不考虑空气阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系 h 20t 5t 2.
(1)球的飞行高度能否达到15m?如能,需要多少飞行时间?
解:(1)当 h 15 时,
20t 5t2 15
t2 4t 3 0
t1 1,t2 3
当球飞行 1s 和 3s 时,它的高度为15m .
1s
3s
15 m
能否结合图象说明?
典型例题
如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线将是一条抛物线,如果不考虑空气阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系 h 20t 5t 2.
(2)球的飞行高度能否达到 20 m 若能,需要多少时间
(2)当 h 20 时,
20t 5t2 20
t2 4t 4 0
t1 t2 2
2s
20 m
当球飞行 2s 时,它的高度为 20m .
典型例题
如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线将是一条抛物线,如果不考虑空气阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系 h 20t 5t 2.
(3)球的飞行高度能否达到 20.5 m 为什么?
(3)当 h 20.5 时,
20t 5t2 20.5
t2 4t 4.1 0
∵( 4)2 4×4.1<0 ,∴方程无实根.
∴球的飞行高度达不到20.5m.
20.5 m
典型例题
如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线将是一条抛物线,如果不考虑空气阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系 h 20t 5t 2.
(4)球从飞出到落地要用多少时间
20t 5t2 0
t 2 4t 0
t1 0,t2 4
当球飞行 0s 和 4s 时,它的高度为 0m ,即 0s时,球从地面飞出,4s 时球落回地面.
(4)当 h 0 时,
小球从飞出到落地要用4s.
0s
4s
0 m
抢答
随堂练习
1.二次函数y x2 2x 1的图象与x轴的交点个数是( )
A.0 B.1 C.2 D.3
2.不与x轴相交的抛物线是( )
A. y 2x2 3 B. y 2x2 3
C. y x2 3x D. y 2(x 1)2 3
3.抛物线y ax2 bx c与x轴的交点坐标为(1,0),(3,0),则方程ax2 bx c 0的解为____________ .
B
x1 1,x2 3
D
抢答
随堂练习
4. 二次函数y ax2 bx c的图象如下图所示,则ax2 bx c 0的解为 ,
ax2 bx c>0的解为 .
x1 1,x2 3
x< 1或x>3
二次函数与一元二次方程
二次函数与一元二次方程的关联:
结合“数、形”解释二次函数与一元二次方程的关系:
没有交点
没有实数根
有一个交点
有两个相等的实数根
有两个交点
有两个不相等的实数根
y ax bx c(a 0)
与x轴的位置关系
ax bx c 0 (a≠0)
根的情况
数
形
二次函数
y ax bx c(a 0)
一元二次方程
ax bx c m(a 0)
y为定值m
教科书第33页练习
第1、2、3题
