鸽巢问题课件(共16张PPT)人教版六年级下册数学
文档属性
| 名称 | 鸽巢问题课件(共16张PPT)人教版六年级下册数学 |  | |
| 格式 | pptx | ||
| 文件大小 | 519.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-19 15:12:27 | ||
图片预览




文档简介
(共16张PPT)
鸽巢问题
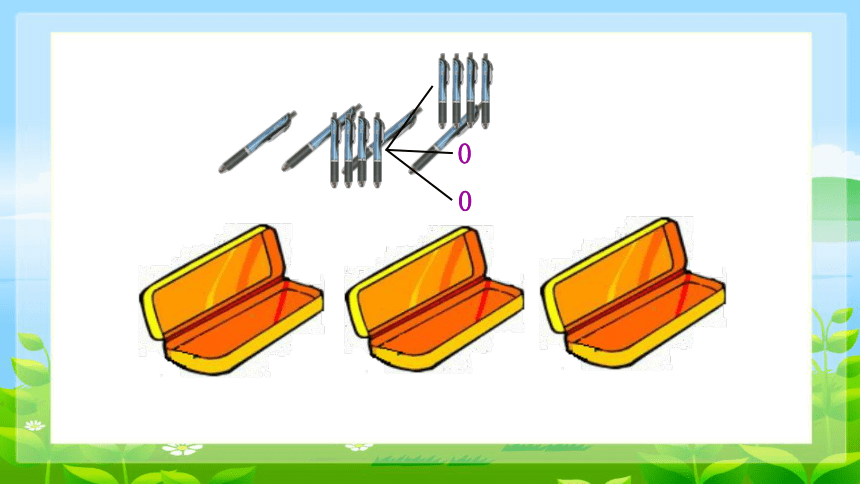
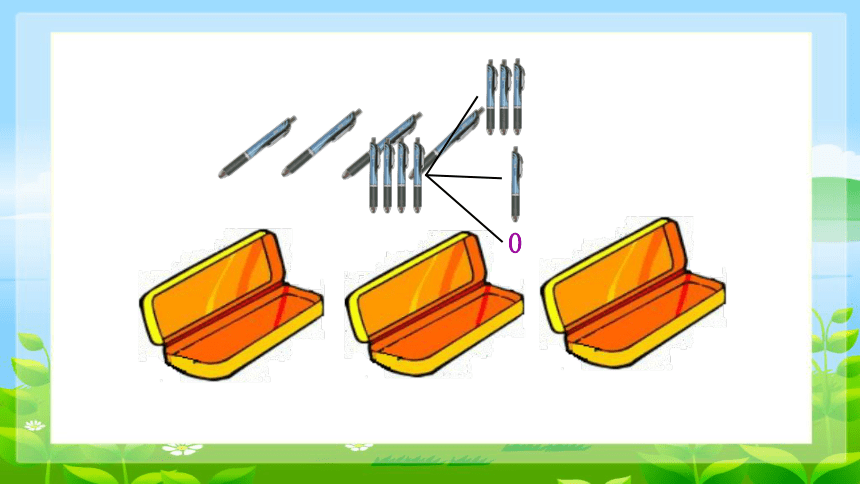
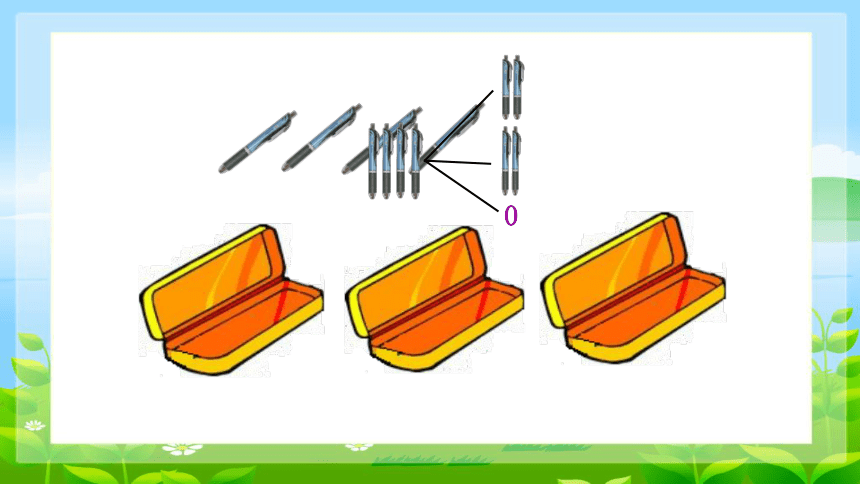
例1:把4支铅笔放进3个文具盒中,不管怎么放,总有一个文具盒里至少有2支铅笔。为什么?
例1:把4支铅笔放进3个文具盒中,不管怎么放,总有一个文具盒里至少有2支铅笔。为什么?
小组活动要求:
请同学们四人小组合作,在小组长的带领下,动手摆一摆、画一画、说一说,把方法记录在学习单上。
0
0
0
0
0
0
0
0
不管怎么放,总有一个文具盒里至少有2支铅笔。
不管怎么放,总有一个文具盒里至少有2支铅笔。
思考:
1.把5支铅笔放进4个文具盒中,总有一个
文具盒中至少放进几支铅笔?为什么?
2.把7支铅笔放进6个文具盒,结果是否一
样呢?
3.把100支铅笔放进99个文具盒呢?
8只鸽子飞回3个鸽笼,总有一个鸽笼里至少飞进( )只鸽子。为什么?
鸽巢问题 ”又称“抽屉原理”,最早是由19世纪德国数学家狄里克雷(Dirichlet)提出的,人们为了纪念他从这么平凡的事情中发现的规律,就用他的名字命名,所以又称狄里克雷原理”。“鸽巢问题”的应用是千变万化的,用它可以解决许多有趣的问题,并且常常能得到一些令人惊异的结果。
任意24人中,总有( )人至少在同一个月生日。为什么?
谈一谈你的收获吧?
谢谢聆听!
鸽巢问题
例1:把4支铅笔放进3个文具盒中,不管怎么放,总有一个文具盒里至少有2支铅笔。为什么?
例1:把4支铅笔放进3个文具盒中,不管怎么放,总有一个文具盒里至少有2支铅笔。为什么?
小组活动要求:
请同学们四人小组合作,在小组长的带领下,动手摆一摆、画一画、说一说,把方法记录在学习单上。
0
0
0
0
0
0
0
0
不管怎么放,总有一个文具盒里至少有2支铅笔。
不管怎么放,总有一个文具盒里至少有2支铅笔。
思考:
1.把5支铅笔放进4个文具盒中,总有一个
文具盒中至少放进几支铅笔?为什么?
2.把7支铅笔放进6个文具盒,结果是否一
样呢?
3.把100支铅笔放进99个文具盒呢?
8只鸽子飞回3个鸽笼,总有一个鸽笼里至少飞进( )只鸽子。为什么?
鸽巢问题 ”又称“抽屉原理”,最早是由19世纪德国数学家狄里克雷(Dirichlet)提出的,人们为了纪念他从这么平凡的事情中发现的规律,就用他的名字命名,所以又称狄里克雷原理”。“鸽巢问题”的应用是千变万化的,用它可以解决许多有趣的问题,并且常常能得到一些令人惊异的结果。
任意24人中,总有( )人至少在同一个月生日。为什么?
谈一谈你的收获吧?
谢谢聆听!
