2024-2025学年甘肃省兰州市西北师大附中高二(上)第一次月考数学试卷(10月份)(含答案)
文档属性
| 名称 | 2024-2025学年甘肃省兰州市西北师大附中高二(上)第一次月考数学试卷(10月份)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 37.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-19 18:50:11 | ||
图片预览


文档简介
2024-2025学年甘肃省兰州市西北师大附中高二(上)第一次月考
数学试卷(10月份)
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.抛掷两枚骰子,所得点数之和为,那么表示的试验结果为( )
A. 一枚点、一枚点 B. 两枚都是点
C. 两枚都是点 D. 一枚点、一枚点,或者两枚都是点
2.对空中飞行的飞机连续射击两次,每次发射一枚炮弹,设事件两弹都击中飞机,事件两弹都没击中飞机,事件恰有一弹击中飞机,事件至少有一弹击中飞机,下列关系不正确的是( )
A. B. C. D.
3.番禺图书馆新谊是一个集知识、信息、文化为一体的综合性阅读场所在一段时间内,若甲同学前往图书馆新馆的概率为,乙前往图书馆新馆的频率为,且甲、乙两人各自行动,则在此段时间内,甲、乙两人至少有一人称往番禺图书馆新馆的概率是( )
A. B. C. D.
4.甲、乙两人轮流投篮,每人每次投一球,约定甲先投,先投中者获胜,一直到有人获胜或每人都已投球次时投篮结束设甲每次投篮投中的概率为,乙每次投篮投中的概率为,且各次投篮互不影响,则甲获胜的概率为( )
A. B. C. D.
5.若两个等差数列和的前项和分别是和,已知,则( )
A. B. C. D.
6.已知等差数列的前项和为,,,则取最大值时的为( )
A. B. C. D. 或
7.已知是等比数列,,,则( )
A. B. C. D.
8.已知数列的前项和为,且,,则的值为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.下列描述正确的是( )
A. 若事件,满足,则与是对立事件
B. 若,,,则事件与相互独立
C. 掷两枚质地均匀的骰子,“第一枚出现奇数点”与“第二枚出现偶数点”不是互斥事件
D. 一个袋子中有个红球,个绿球,采用不放回方式从中依次随机地取出两球,第二次取到红球的概率是
10.已知等差数列的前项和为,公差,,是与的等比中项,则下列选项正确的是( )
A. B.
C. 当且仅当时,取得最大值 D. 当时,的最大值为
11.已知数列满足,,,则( )
A. 是等比数列 B.
C. 是递增数列 D.
三、填空题:本题共3小题,每小题5分,共15分。
12.设,,为三个随机事件,若与互斥,与对立,且,,则 .
13.在各项均为正数的等比数列中公比,若,,,记数列的前项和为则的最大值为______.
14.等差数列前项和为,正项等比数列满足,则 ______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知数列,满足,.
数列是否为等差数列?说明理由.
求的通项公式.
16.本小题分
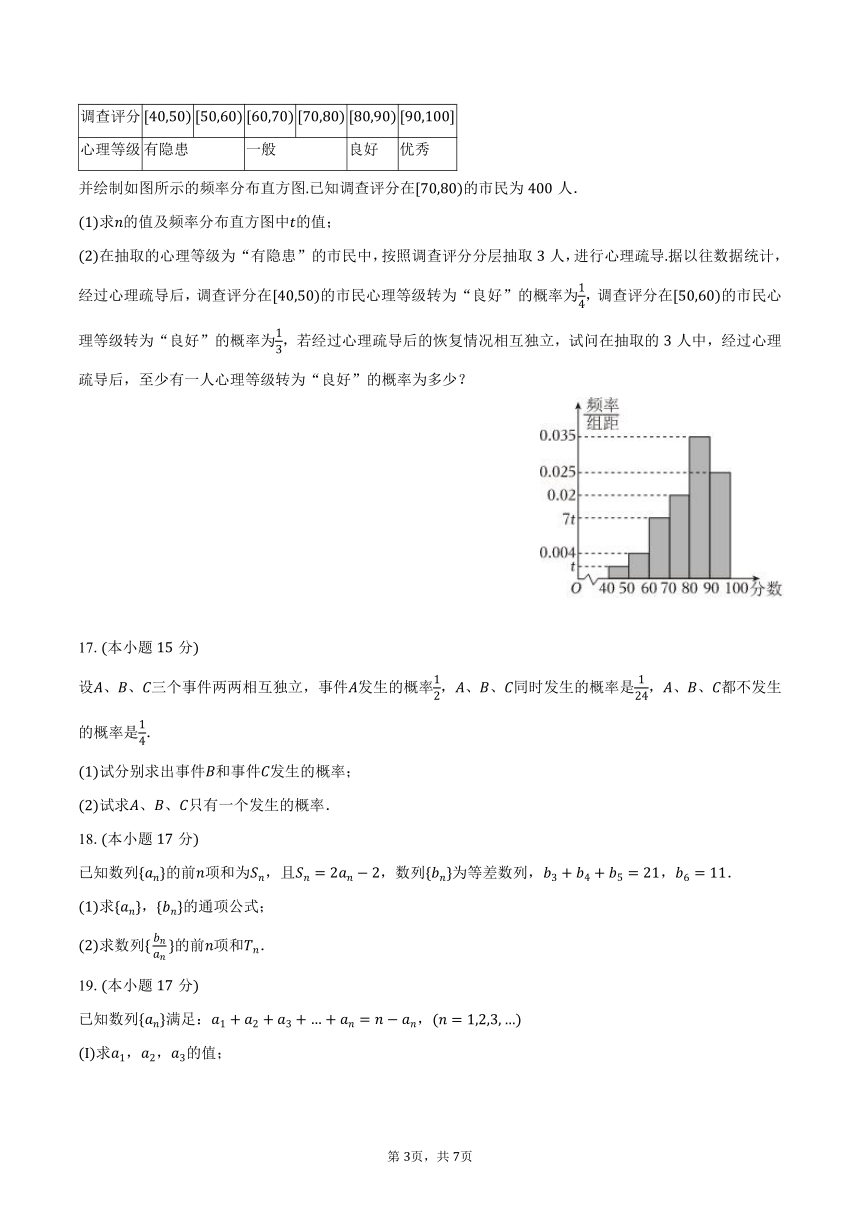
习近平总书记指出:“要健全社会心理服务体系和疏导机制、危机干预机制,塑造自尊自信、理性平和、亲善友爱的社会心态”在年新冠肺炎疫情防控阻击战中,心理医生的相关心理疏导起到了重要作用某心理调查机构为了解市民在疫情期的心理健康状况,随机抽取位市民进行心理健康问卷调查,按所得评分满分分从低到高将心理健康状况分为四个等级:
调查评分
心理等级 有隐患 一般 良好 优秀
并绘制如图所示的频率分布直方图已知调查评分在的市民为人.
求的值及频率分布直方图中的值;
在抽取的心理等级为“有隐患”的市民中,按照调查评分分层抽取人,进行心理疏导据以往数据统计,经过心理疏导后,调查评分在的市民心理等级转为“良好”的概率为,调查评分在的市民心理等级转为“良好”的概率为,若经过心理疏导后的恢复情况相互独立,试问在抽取的人中,经过心理疏导后,至少有一人心理等级转为“良好”的概率为多少?
17.本小题分
设、、三个事件两两相互独立,事件发生的概率,、、同时发生的概率是,、、都不发生的概率是.
试分别求出事件和事件发生的概率;
试求、、只有一个发生的概率.
18.本小题分
已知数列的前项和为,且,数列为等差数列,,.
求,的通项公式;
求数列的前项和.
19.本小题分
已知数列满足:,
Ⅰ求,,的值;
Ⅱ求证:数列是等比数列;
Ⅲ令,如果对任意,都有,求实数的取值范围.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:数列是等差数列,由得,,
因为,所以两边同时取倒数得,
即,
所以数列是以为首项、公差的等差数列;
由可得,
所以的通项公式是.
16.解:由已知条件可得,每组的纵坐标的和乘以组距为,
所以,解得.
由知,
所以调查评分在的人数占调查评分在人数的,
若按分层抽样抽取人,
则调查评分在有人,有人,
因为经过心理疏导后的恢复情况相互独立,
所以选出的人经过心理疏导后,
心理等级均达不到良好的概率为,
所以经过心理疏导后,至少有一人心理等级转为良好的概率为.
17.解:由题意得:.
,即.
解得:,或,.
设、、只有一个发生的概率为
当,时.
则.
当,时,同理可得:.
综上:、、只有一个发生的概率为.
18.解:当时,,解得.
当时,,,
两式相减得,即,
数列是首项、公比均为的等比数列,故.
设等差数列的公差为,
由,可得,又,
,解得,故.
令,由知,
则,
,
,得,
所以.
19.解:Ⅰ由题意得:,则,
,则,
,则;
Ⅱ由题可知:,
,
可得,
即,
又,
所以数列是以为首项,以为公比的等比数列;
Ⅲ由Ⅱ可得,
所以,
所以
,
由可得,
所以
故有最大值
所以对任意,有,
如果对任意,都有,
即成立,
则,故有:,
解得或,
所以实数的取值范围是.
第1页,共1页
数学试卷(10月份)
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.抛掷两枚骰子,所得点数之和为,那么表示的试验结果为( )
A. 一枚点、一枚点 B. 两枚都是点
C. 两枚都是点 D. 一枚点、一枚点,或者两枚都是点
2.对空中飞行的飞机连续射击两次,每次发射一枚炮弹,设事件两弹都击中飞机,事件两弹都没击中飞机,事件恰有一弹击中飞机,事件至少有一弹击中飞机,下列关系不正确的是( )
A. B. C. D.
3.番禺图书馆新谊是一个集知识、信息、文化为一体的综合性阅读场所在一段时间内,若甲同学前往图书馆新馆的概率为,乙前往图书馆新馆的频率为,且甲、乙两人各自行动,则在此段时间内,甲、乙两人至少有一人称往番禺图书馆新馆的概率是( )
A. B. C. D.
4.甲、乙两人轮流投篮,每人每次投一球,约定甲先投,先投中者获胜,一直到有人获胜或每人都已投球次时投篮结束设甲每次投篮投中的概率为,乙每次投篮投中的概率为,且各次投篮互不影响,则甲获胜的概率为( )
A. B. C. D.
5.若两个等差数列和的前项和分别是和,已知,则( )
A. B. C. D.
6.已知等差数列的前项和为,,,则取最大值时的为( )
A. B. C. D. 或
7.已知是等比数列,,,则( )
A. B. C. D.
8.已知数列的前项和为,且,,则的值为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.下列描述正确的是( )
A. 若事件,满足,则与是对立事件
B. 若,,,则事件与相互独立
C. 掷两枚质地均匀的骰子,“第一枚出现奇数点”与“第二枚出现偶数点”不是互斥事件
D. 一个袋子中有个红球,个绿球,采用不放回方式从中依次随机地取出两球,第二次取到红球的概率是
10.已知等差数列的前项和为,公差,,是与的等比中项,则下列选项正确的是( )
A. B.
C. 当且仅当时,取得最大值 D. 当时,的最大值为
11.已知数列满足,,,则( )
A. 是等比数列 B.
C. 是递增数列 D.
三、填空题:本题共3小题,每小题5分,共15分。
12.设,,为三个随机事件,若与互斥,与对立,且,,则 .
13.在各项均为正数的等比数列中公比,若,,,记数列的前项和为则的最大值为______.
14.等差数列前项和为,正项等比数列满足,则 ______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知数列,满足,.
数列是否为等差数列?说明理由.
求的通项公式.
16.本小题分
习近平总书记指出:“要健全社会心理服务体系和疏导机制、危机干预机制,塑造自尊自信、理性平和、亲善友爱的社会心态”在年新冠肺炎疫情防控阻击战中,心理医生的相关心理疏导起到了重要作用某心理调查机构为了解市民在疫情期的心理健康状况,随机抽取位市民进行心理健康问卷调查,按所得评分满分分从低到高将心理健康状况分为四个等级:
调查评分
心理等级 有隐患 一般 良好 优秀
并绘制如图所示的频率分布直方图已知调查评分在的市民为人.
求的值及频率分布直方图中的值;
在抽取的心理等级为“有隐患”的市民中,按照调查评分分层抽取人,进行心理疏导据以往数据统计,经过心理疏导后,调查评分在的市民心理等级转为“良好”的概率为,调查评分在的市民心理等级转为“良好”的概率为,若经过心理疏导后的恢复情况相互独立,试问在抽取的人中,经过心理疏导后,至少有一人心理等级转为“良好”的概率为多少?
17.本小题分
设、、三个事件两两相互独立,事件发生的概率,、、同时发生的概率是,、、都不发生的概率是.
试分别求出事件和事件发生的概率;
试求、、只有一个发生的概率.
18.本小题分
已知数列的前项和为,且,数列为等差数列,,.
求,的通项公式;
求数列的前项和.
19.本小题分
已知数列满足:,
Ⅰ求,,的值;
Ⅱ求证:数列是等比数列;
Ⅲ令,如果对任意,都有,求实数的取值范围.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:数列是等差数列,由得,,
因为,所以两边同时取倒数得,
即,
所以数列是以为首项、公差的等差数列;
由可得,
所以的通项公式是.
16.解:由已知条件可得,每组的纵坐标的和乘以组距为,
所以,解得.
由知,
所以调查评分在的人数占调查评分在人数的,
若按分层抽样抽取人,
则调查评分在有人,有人,
因为经过心理疏导后的恢复情况相互独立,
所以选出的人经过心理疏导后,
心理等级均达不到良好的概率为,
所以经过心理疏导后,至少有一人心理等级转为良好的概率为.
17.解:由题意得:.
,即.
解得:,或,.
设、、只有一个发生的概率为
当,时.
则.
当,时,同理可得:.
综上:、、只有一个发生的概率为.
18.解:当时,,解得.
当时,,,
两式相减得,即,
数列是首项、公比均为的等比数列,故.
设等差数列的公差为,
由,可得,又,
,解得,故.
令,由知,
则,
,
,得,
所以.
19.解:Ⅰ由题意得:,则,
,则,
,则;
Ⅱ由题可知:,
,
可得,
即,
又,
所以数列是以为首项,以为公比的等比数列;
Ⅲ由Ⅱ可得,
所以,
所以
,
由可得,
所以
故有最大值
所以对任意,有,
如果对任意,都有,
即成立,
则,故有:,
解得或,
所以实数的取值范围是.
第1页,共1页
同课章节目录
