人教版2024-2025学年八年级数学上册专题13.1垂直平分线中的几何综合(压轴题专项讲练)(学生版+解析)
文档属性
| 名称 | 人教版2024-2025学年八年级数学上册专题13.1垂直平分线中的几何综合(压轴题专项讲练)(学生版+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-20 19:19:47 | ||
图片预览



文档简介
专题13.1 垂直平分线中的几何综合
正向思维:是一类常规性的、传统的思维形式,指的是大家按照自上而下,由近及远、从左到右、从可知到未知等一般而言的线性方向做出探究问题的思维途径。
逆向思维:是指在剖析、破解数学难题进程中,可以灵活转换思维方向,从常规思维的相反方向出发进行探索的思维方式,比如正向思维无法解决问题时可反其道而行采取逆向思维,直接证明有困难时可采用间接证明。
一、线段垂直平分线的性质
线段垂直平分线上的点与这条线段两个端点的距离相等.反过来,与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
二、线段垂直平分线的判定
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.(这样的点需要找两个)
【典例1】如图,的两条高与交于点,,.
(1)求证:;
(2)连结,试说明:是的垂直平分线;
(3)是射线上一点,且,动点从点出发,沿线段以每秒1个单位长度的速度向终点A运动,同时动点从点出发,沿射线以每秒3个单位长度的速度运动,当点到达点A时,,两点同时停止运动,设运动时间为秒,当与全等时,求的值.
【思路点拨】
(1)证明,即可得到;
(2)先证明,得到,进而得到点在的垂直平分线上,再根据得到点在的垂直平分线上,即可得到是的垂直平分线;
(3)当点在延长线上时,设运动秒,根据得到,,根据得到,进而得到,求得;当点在之间时,设运动秒,根据得到,,根据得到,进而得到,求得,问题得解.
【解题过程】
(1)证明:、是高,
,
在与中,
,
;
(2)证明:,,
,
,
、是高,
.
在与中,,
,
,
点在的垂直平分线上.
,
点在的垂直平分线上,
是的垂直平分线;
(3)解:①如图1,当点在延长线上时,
设运动秒,、分别运动到如图位置,.
,,
当时,.
,,
,
解得.
②如图2,当点在之间时,
设运动秒,、分别运动到如图位置,.
,,
当时,.
,,
,
解得.
综上所述,或4.
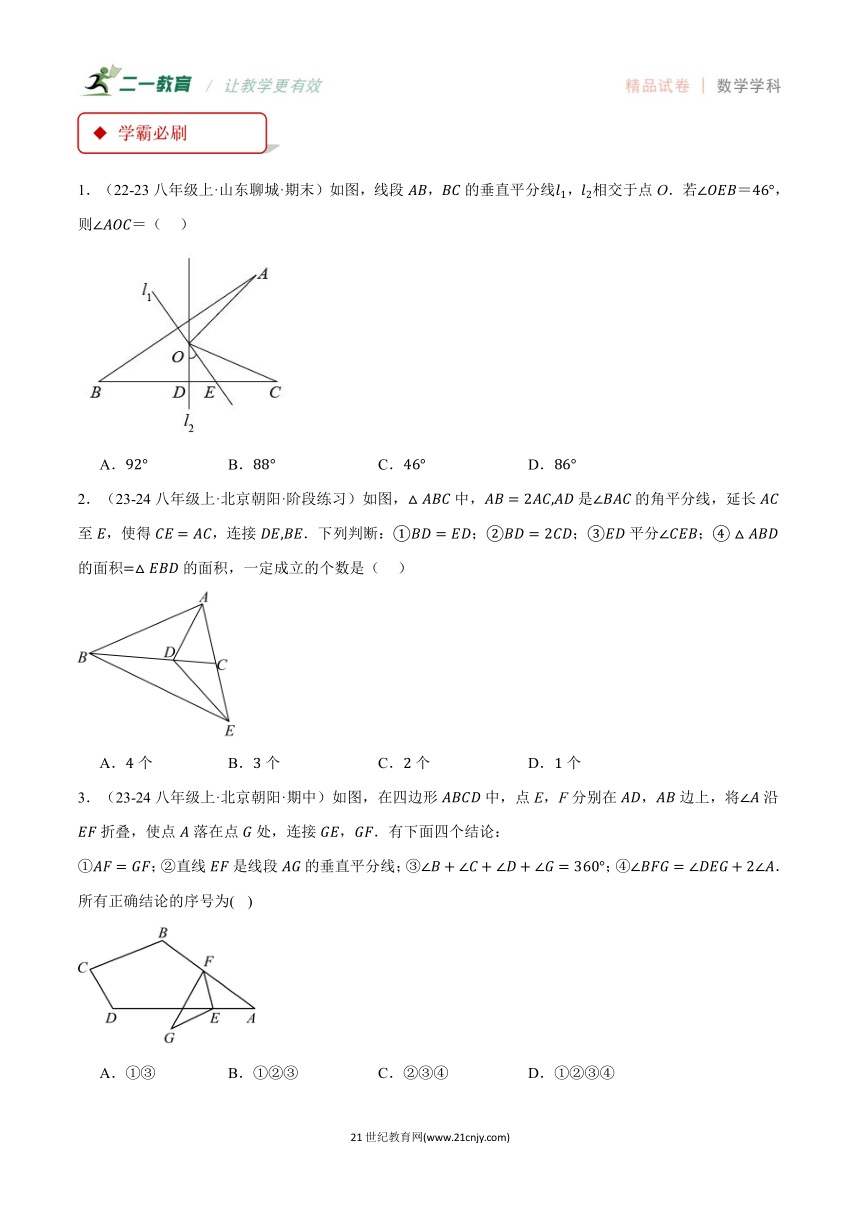
1.(22-23八年级上·山东聊城·期末)如图,线段,的垂直平分线,相交于点O.若,则( )
A. B. C. D.
2.(23-24八年级上·北京朝阳·阶段练习)如图,中,是的角平分线,延长至,使得,连接.下列判断:;;平分;的面积的面积,一定成立的个数是( )
A.个 B.个 C.个 D.个
3.(23-24八年级上·北京朝阳·期中)如图,在四边形中,点E,F分别在,边上,将沿折叠,使点落在点处,连接,.有下面四个结论:
①;②直线是线段的垂直平分线;③;④.
所有正确结论的序号为( )
A.①③ B.①②③ C.②③④ D.①②③④
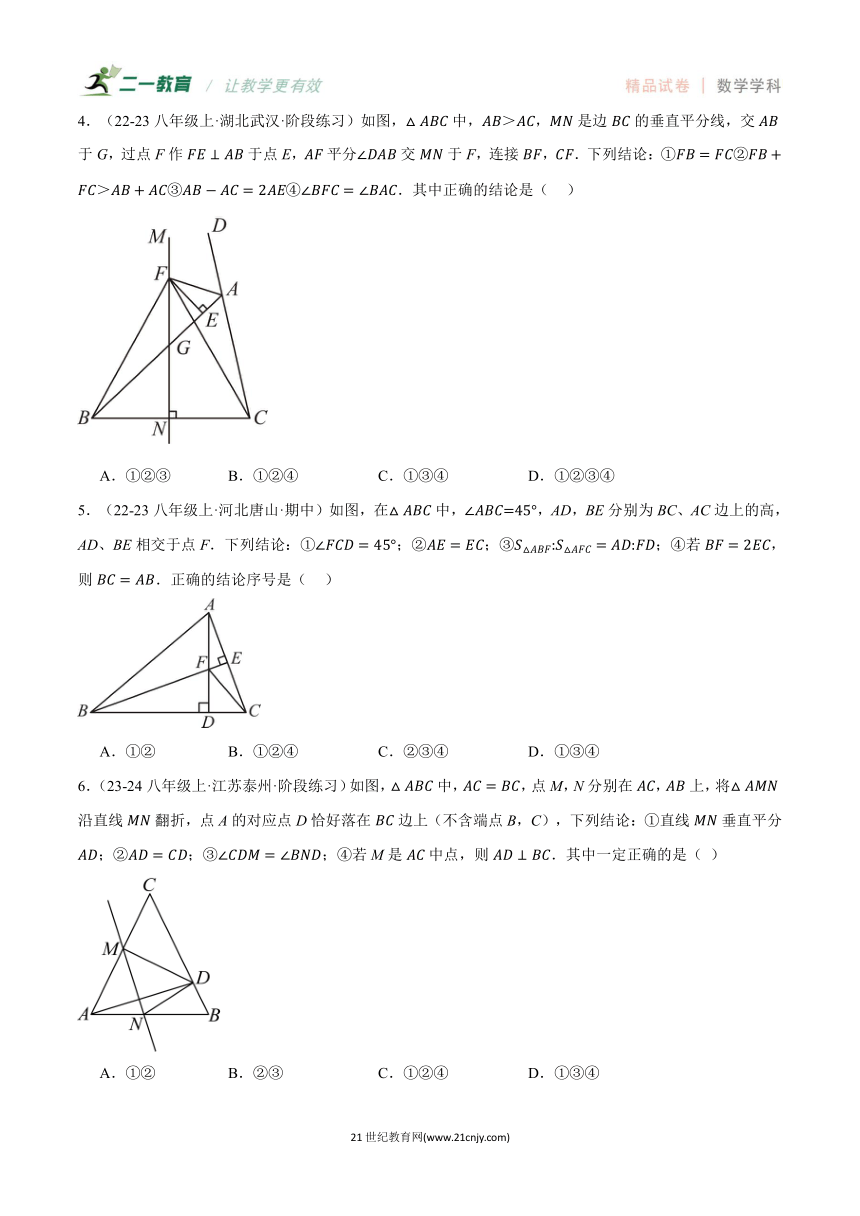
4.(22-23八年级上·湖北武汉·阶段练习)如图,中,,是边的垂直平分线,交于G,过点F作于点E,平分交于F,连接,.下列结论:①②③④.其中正确的结论是( )
A.①②③ B.①②④ C.①③④ D.①②③④
5.(22-23八年级上·河北唐山·期中)如图,在中,,AD,BE分别为BC、AC边上的高,AD、BE相交于点F.下列结论:①;②;③;④若,则.正确的结论序号是( )
A.①② B.①②④ C.②③④ D.①③④
6.(23-24八年级上·江苏泰州·阶段练习)如图,中,,点M,N分别在,上,将沿直线翻折,点A的对应点D恰好落在边上(不含端点B,C),下列结论:①直线垂直平分;②;③;④若M是中点,则.其中一定正确的是( )
A.①② B.②③ C.①②④ D.①③④
7.(22-23八年级上·重庆巴南·期中)如图,在中,,以为边,作,满足,点为上一点,连接,,下列结论:①;②;③若,则;④.正确的有( )
A.1个 B.2个 C.3个 D.4个
8.(22-23七年级下·广西南宁·期末)如图,在中,D为中点,,,于点F,,,则的长为 .
9.(23-24八年级上·河北唐山·阶段练习)如图,在中,,,分别为,边上的高,,相交于点,连接,则下列结论:;;;若,则周长等于的长其中正确的有 写出所有正确结论的序号
10.(22-23八年级下·黑龙江哈尔滨·阶段练习)如图,在△ABC中,∠C=45°,AD⊥BC于D,F为AC上一点,连接BF交AD于E,过F作MN⊥FB交BA延长线于M,交BC于N,若点M恰在BN的垂直平分线上,且DE:BN=1:7,S△ABD=15,则S△ABE= .
11.(23-24八年级上·福建莆田·开学考试)如图,在中,,的角平分线和的平分线相交于点,交于点,交的延长线于点,过点作交的延长线于点,交的延长线于点,连接并延长交于点,则下列结论:①;②;③;④;其中正确的有 .(填序号)
12.(2023·江苏无锡·模拟预测)请用无刻度的直尺和圆规作图:
(1)如图1,在上求作点D,使;
(2)如图2,若点D在边上,在上求作点E,使.
13.(2023·江苏扬州·模拟预测)尺规作图:保留作图痕迹,不要求写作法.
(1)过点作一条直线,使其平分的面积.
(2)在上求作一点,使与面积相等.
(3)过点作一条直线,使其平分的面积.
14.(2024七年级下·全国·专题练习)如图,在中,,分别垂直平分边和边,交边于,两点,与相交于点.
(1)若,则的周长为 ;
(2)若,求的度数.
15.(22-23八年级上·江苏南京·阶段练习)如图,在中,垂直平分平分.
(1)若,求的度数;
(2)若,与的周长之差为,且的面积为,求的面积.
16.(22-23八年级上·福建福州·期中)如图,在△ABC中,∠ACB=90°.
(1)在AC的右侧作△DCF,使点F在AC上,且△DCF≌△ABC;(要求:尺规作图,保留作图痕迹)
(2)在(1)的条件下,连接BD交AC于点P.若AC=2BC=4,求PC的长.
17.(23-24八年级上·四川成都·开学考试)如图:在中,,,射线、的夹角为,过点作于点,直线交于点,连接.
(1)如图,若射线、都在的内部,且点与点关于对称,求证:;
(2)如图,若射线在的内部,射线在的外部,其他条件不变,求证:;
(3)如图,若射线、都在的外部,其他条件不变,若,,,求的长.
18.(23-24八年级上·辽宁·期中)在中,,,射线,的夹角为,过点作于点,直线交于点,连接.
(1)如图1,射线,都在内部.
①若,,则 ;
②作点关于直线的对称点,在图1中找出与线段相等的线段,并证明.
(2)如图2,射线在的内部,射线在的外部,其它条件不变,探究线段之间的数量关系,并证明.
21世纪教育网(www.21cnjy.com)
专题13.1 垂直平分线中的几何综合
正向思维:是一类常规性的、传统的思维形式,指的是大家按照自上而下,由近及远、从左到右、从可知到未知等一般而言的线性方向做出探究问题的思维途径。
逆向思维:是指在剖析、破解数学难题进程中,可以灵活转换思维方向,从常规思维的相反方向出发进行探索的思维方式,比如正向思维无法解决问题时可反其道而行采取逆向思维,直接证明有困难时可采用间接证明。
一、线段垂直平分线的性质
线段垂直平分线上的点与这条线段两个端点的距离相等.反过来,与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
二、线段垂直平分线的判定
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.(这样的点需要找两个)
【典例1】如图,的两条高与交于点,,.
(1)求证:;
(2)连结,试说明:是的垂直平分线;
(3)是射线上一点,且,动点从点出发,沿线段以每秒1个单位长度的速度向终点A运动,同时动点从点出发,沿射线以每秒3个单位长度的速度运动,当点到达点A时,,两点同时停止运动,设运动时间为秒,当与全等时,求的值.
【思路点拨】
(1)证明,即可得到;
(2)先证明,得到,进而得到点在的垂直平分线上,再根据得到点在的垂直平分线上,即可得到是的垂直平分线;
(3)当点在延长线上时,设运动秒,根据得到,,根据得到,进而得到,求得;当点在之间时,设运动秒,根据得到,,根据得到,进而得到,求得,问题得解.
【解题过程】
(1)证明:、是高,
,
在与中,
,
;
(2)证明:,,
,
,
、是高,
.
在与中,,
,
,
点在的垂直平分线上.
,
点在的垂直平分线上,
是的垂直平分线;
(3)解:①如图1,当点在延长线上时,
设运动秒,、分别运动到如图位置,.
,,
当时,.
,,
,
解得.
②如图2,当点在之间时,
设运动秒,、分别运动到如图位置,.
,,
当时,.
,,
,
解得.
综上所述,或4.
1.(22-23八年级上·山东聊城·期末)如图,线段,的垂直平分线,相交于点O.若,则( )
A. B. C. D.
【思路点拨】
根据线段垂直平分线的性质结合三角形外角性质得到,再利用垂直的定义结合直角三角形两锐角互余得到,计算即可.
【解题过程】
解:如图,连接BO并延长至点P,与线段AB交于F,
∵,是、的垂直平分线,
∴,,,
∴,
∴,,
∴,
∵,,
∴,
∴,
故选:B
2.(23-24八年级上·北京朝阳·阶段练习)如图,中,是的角平分线,延长至,使得,连接.下列判断:;;平分;的面积的面积,一定成立的个数是( )
A.个 B.个 C.个 D.个
【思路点拨】
利用三角形的角平分线,中线和垂直平分线进行判断即可,
【解题过程】
解:如图,延长交于点,过作于点,
∵,,
∴,
又∵是的平分线,
∴垂直平分,
∴,故正确;
∵,
∴,,
∴,即,故正确;
由题意可知与不一定相等,
则不一定成立;
∵,垂直平分,
∴,
∴,故正确;
综上 正确;
故选:.
3.(23-24八年级上·北京朝阳·期中)如图,在四边形中,点E,F分别在,边上,将沿折叠,使点落在点处,连接,.有下面四个结论:
①;②直线是线段的垂直平分线;③;④.
所有正确结论的序号为( )
A.①③ B.①②③ C.②③④ D.①②③④
【思路点拨】
本题考查翻折变换,线段垂直平分线的判定,多边形内角和公式,三角形外角性质,掌握翻折不变性,以及相关性质是解题的关键.
由翻折不变性,可判断①正确;由翻折不变性,可得,,可判断②正确;由多边形内角和公式和翻折不变性,可判断③正确;由三角形外角性质和翻折不变性,可判断④正确;即可解答.
【解题过程】
解: 是由翻折得到的,
,
故①正确;
是由翻折得到的,是由翻折得到的,
,,
点E,点F都在的垂直平分线上,
直线是线段的垂直平分线,
故②正确;
是由翻折得到的,
故③正确;
设与交于点H,
是由翻折得到的,
故④正确;
综上,正确的有:①②③④,
故选:D.
4.(22-23八年级上·湖北武汉·阶段练习)如图,中,,是边的垂直平分线,交于G,过点F作于点E,平分交于F,连接,.下列结论:①②③④.其中正确的结论是( )
A.①②③ B.①②④ C.①③④ D.①②③④
【思路点拨】
根据线段垂直平分线的性质,得到;过点F作于点H,证明,得到,结合平分,得到,继而,可证明;利用斜边大于直角边,证明;利用等腰三角形的性质,全等三角形的性质,结合三角形内角和定理证明.
【解题过程】
解:∵是边的垂直平分线,
∴;
故①正确;
过点F作于点H,
∵平分,,,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
故③正确;
∵,
∴,
∴,
∴,
故②正确;
∵,,
∴,
∴,
故④正确;
故选D.
5.(22-23八年级上·河北唐山·期中)如图,在中,,AD,BE分别为BC、AC边上的高,AD、BE相交于点F.下列结论:①;②;③;④若,则.正确的结论序号是( )
A.①② B.①②④ C.②③④ D.①③④
【思路点拨】
根据垂直定义可得,再利用,得到,从而可证明,进而得到,即可判断①;根据,,即可判断②,根据三角形面积公式和它们有一条公共边可得,即可判断③,若,根据可以得到,从而可得是的中点,然后可以推出是的垂直平分线,最后由线段垂直平分线的性质即可判断④.
【解题过程】
解:,
,
,
,
,
,
,
,
,
,
,
,
,故①正确;
,,
,故②不正确;
,
,故③正确;
,
,
,
为的中点,
,
为线段的垂直平分线,
,故④正确,
所以,正确结论的序号是:①③④,
故选:D.
6.(23-24八年级上·江苏泰州·阶段练习)如图,中,,点M,N分别在,上,将沿直线翻折,点A的对应点D恰好落在边上(不含端点B,C),下列结论:①直线垂直平分;②;③;④若M是中点,则.其中一定正确的是( )
A.①② B.②③ C.①②④ D.①③④
【思路点拨】
①根据将沿直线翻折,点A的对应点D恰好落在边上(不含端点B,C),证明直线垂直平分,故①正确;
②证明与不一定相等,得到与不一定相等,故②错误;
③先由①得,直线垂直平分,则,,再根据”等边对等角“证明,,则,再根据是的一个外角,是的一个外角,证明,,进一步证明,根据,得到,则,然后根据,证明,从而得到,故③正确;
④先根据是的中点,证明,再由①得,直线垂直平分,则,再证明,最后证明,即,故④正确.
【解题过程】
解:①∵将沿直线翻折,点A的对应点D恰好落在边上(不含端点B,C),
∴直线垂直平分,
故①正确;
②∵,
∴,
∴
又∵,
∴与不一定相等,
∴与不一定相等,
∴与不一定相等,
故②错误;
③由①得,直线垂直平分,
∴,,
∴,,
∴
∵是的一个外角,是的一个外角,
∴,
∴,
∴,
∴,
∴,
∴
又∵,
∴
即,
又∵(已证),
∴,
故③正确;
④∵是的中点,
∴,
∵,
∴,
∴,,
又,
∴,
∴,
∴,
故④正确;
综上所述,一定正确的有①③④,
故选:D.
7.(22-23八年级上·重庆巴南·期中)如图,在中,,以为边,作,满足,点为上一点,连接,,下列结论:①;②;③若,则;④.正确的有( )
A.1个 B.2个 C.3个 D.4个
【思路点拨】
延长至G,使,从而得到,进一步证明,且,利用证明,则,所以①是正确的,通过线段的等量代换运算推导出④是正确的,设,则,因为,所以,接着用x表示出,再计算出,故③是正确的,当时,可以推导出,否则不垂直于,故②是错误的.
【解题过程】
解:如图,延长至G,使,设与交于点M,
∵,
∴,
∴垂直平分,
∴,
∴,
∵,
∴,
∴,
∴,
在中,
,
∴,
∴,
∴①是正确的;
∵,
∴,
∴平分,
当时,,则,
当时,,则无法说明,
∴②是不正确的;
设,则,
∴,
∵,
∴,
∴,
∴,
∴,
∴③是正确的;
∵,
∴,
∵,
∴,
∴
∴④是正确的,
故选:C.
8.(22-23七年级下·广西南宁·期末)如图,在中,D为中点,,,于点F,,,则的长为 .
【思路点拨】
连接,过点E作,交的延长线于N,由,可得;由D为中点,,则可得;证明,再证明即可求得结果.
【解题过程】
解:连接,过点E作,交的延长线于N,如图,
∵,,
∴;
∵D为中点,,
∴;
∵,,
∴,
∵,
∴,
∴;
∵,,,
∴,
∴,
∴,
即,
∴.
∴
故答案为:.
9.(23-24八年级上·河北唐山·阶段练习)如图,在中,,,分别为,边上的高,,相交于点,连接,则下列结论:;;;若,则周长等于的长其中正确的有 写出所有正确结论的序号
【思路点拨】
本题考查了全等三角形的判定与性质,掌握全等三角形的判定与性质,线段垂直平分线的性质,外角的性质,三角形内角和定理,等腰三角形的性质是解决问题的关键.
延长交于,先利用“”证明,得出,,可判断①符合题意;由,得出,再由三角形外角的性质,可判断②不符合题意;由,,得出,得出,可判断③符合题意;由,,可证明垂直平分,得出,,得出的周长,可判断④符合题意;即可得出答案.
【解题过程】
解:如图,延长交于,
,分别为,边上的高,
,
,
,
,
,
,
,
在和中,
,
,
,,故①符合题意;
,
,
,
,故②不符合题意;
,,
,
,故③符合题意;
,,
,
,
,
垂直平分,
,,
的周长
,故④符合题意.
故答案为:.
10.(22-23八年级下·黑龙江哈尔滨·阶段练习)如图,在△ABC中,∠C=45°,AD⊥BC于D,F为AC上一点,连接BF交AD于E,过F作MN⊥FB交BA延长线于M,交BC于N,若点M恰在BN的垂直平分线上,且DE:BN=1:7,S△ABD=15,则S△ABE= .
【思路点拨】
过点F作FG⊥BN于点G,根据已知条件证明△ABD≌△BFG,可得BD=FG,AD=BG,再证明△BDE≌△FGN可得DE=GN,根据DE:BN=1:7,可得GN:BN=1:7,设ED=x,DE:BG=1:6,可得AD=BG=6x, AE=5x,然后根据S△ABD=15,进而可得S△ABE.
【解题过程】
解:如图,过点F作FG⊥BN于点G,
∵AD⊥BC,
∴∠ADC=90°,
∵∠C=45°,
∴∠DAC=45°,
∵MN⊥FB,
∴∠FBN+∠FNB=90°,
∵点M恰在BN的垂直平分线上,
∴MB=MN,
∴∠ABN=∠FNB,
∴∠ABN+∠BAD=90°,
∴∠BAD=∠FBN,
∵∠AFB=∠FBC+∠C=∠BAD+∠DAC=∠BAF,
∴BA=BF,
在△ABD和△BFG中,
,
∴△ABD≌△BFG(AAS),
∴BD=FG,AD=BG,
∵∠BED+∠EBD=90°,∠BAD+∠ABD=90°,
∴∠BED=∠ABD=∠BFG=∠FNG,
在△BDE和△FGN中,
,
∴△BDE≌△FGN(AAS),
∴DE=GN,
∵DE:BN=1:7,
∴GN:BN=1:7,
设ED=x,
∴DE:BG=1:6,
∴AD=BG=6x,
∴AE=AD﹣ED=6x﹣x=5x,
∵S△ABD=15,
∴S△ABE==.
故答案为:.
11.(23-24八年级上·福建莆田·开学考试)如图,在中,,的角平分线和的平分线相交于点,交于点,交的延长线于点,过点作交的延长线于点,交的延长线于点,连接并延长交于点,则下列结论:①;②;③;④;其中正确的有 .(填序号)
【思路点拨】
①利用角平分线的性质以及三角形外角的性质,求解即可;
②③延长与交于点,利用全等三角形的判定与性质求解即可;
④在上截取,利用垂直平分线的性质以及全等三角形的性质,求解即可.
【解题过程】
解:设,,
∵平分,平分,
∴,
由三角形外角的性质可得:
∴①正确;
延长与交于点,如下图:
∵
∴
∵平分
∴
又∵,
∴
∴
∵
∴
又∵,
∴
∴
∴②正确;
同理可得:
∴,③正确;
在上截取,则是的垂直平分线,如下图:
∴
∵
∴,
又∵
∴
∵,
∴
∵
∴
∴
又∵
∴
又∵
∴
∴
∴④正确
故答案为:①②③④
12.(2023·江苏无锡·模拟预测)请用无刻度的直尺和圆规作图:
(1)如图1,在上求作点D,使;
(2)如图2,若点D在边上,在上求作点E,使.
【思路点拨】
(1)作的垂直平分线与的交点即为所求;
(2)如图:由题意得,只要作即可,由第(1)问得,,只要作即可.
【解题过程】
(1)解:如图:
作的垂直平分线与交于D点,
,
与高相同,
.
如图1:点D即为所求;
(2)如图:
由题意得,只要作即可,
作的垂直平分线交于点,
由第(1)问得,,
故只要作即可,
连接、,要使得,只要作,
根据“夹在平行线之间的垂线段相等”,即,高相等,
只要作,
根据“同位角相等,两直线平行”,作,交于点,
如图2:点E即为所求.
13.(2023·江苏扬州·模拟预测)尺规作图:保留作图痕迹,不要求写作法.
(1)过点作一条直线,使其平分的面积.
(2)在上求作一点,使与面积相等.
(3)过点作一条直线,使其平分的面积.
【思路点拨】
(1)作出线段的垂直平分线,垂足为,作直线即可;
(2)作,交与点,点即为所求;
(3)根据(1)的方法作出中线,连接,根据(2)的方法作,交与点,作直线即可.
【解题过程】
(1)解: 如图直线即为所求;
(2)解: 如图,点即为所求;
∵,
∴,
∴,
(3)解:如图,直线即为所求.
理由如下,
∵是的中线,
∴,
∵,
∴,
∴,
∴直线平分的面积.
14.(2024七年级下·全国·专题练习)如图,在中,,分别垂直平分边和边,交边于,两点,与相交于点.
(1)若,则的周长为 ;
(2)若,求的度数.
【思路点拨】
本题考查垂直平分线,三角形内角和的知识,解题的关键是掌握垂直平分线的性质,三角形的内角和,即可.
(1)根据垂直平分线的性质,则,,根据,的周长为:,即可;
(2)垂直平分线的性质,则,,根据三角形内角和,则,再根据对顶角相等,则,根据三角形内角和,则,,最后根据,即可.
【解题过程】
(1)∵,分别垂直平分边和边,
∴,,
∵,
∴,
∵的周长为:,
∴,
故答案为:.
(2)∵,分别垂直平分边和边,
∴,,
∵,
∴,
∵,,
∴,
∵,,
∴,
∴,
∴,
∴.
15.(22-23八年级上·江苏南京·阶段练习)如图,在中,垂直平分平分.
(1)若,求的度数;
(2)若,与的周长之差为,且的面积为,求的面积.
【思路点拨】
(1)由线段垂直平分线的性质结合三角形外角的性质易求出,再根据角平分线的定义即得出,最后根据三角形内角和定理求解即可;
(2)由线段垂直平分线的性质结合与的周长之差为,即可求出.过点D作于H.由的面积为,,可求出,结合角平分线的性质定理可得出,即可计算.
【解题过程】
(1)解:∵垂直平分,
∴,
∴.
∵,
∴.
∵平分,
∴,
∴;
(2)解:∵垂直平分,
∴,,,
∵,,,
∴,
∴,
∴,即.
过点D作于H.
∵的面积为,且,,
∴,
∴.
∵平分,
∴.
∴.
16.(22-23八年级上·福建福州·期中)如图,在△ABC中,∠ACB=90°.
(1)在AC的右侧作△DCF,使点F在AC上,且△DCF≌△ABC;(要求:尺规作图,保留作图痕迹)
(2)在(1)的条件下,连接BD交AC于点P.若AC=2BC=4,求PC的长.
【思路点拨】
(1)在CA上截取CF=CB,然后分别以C、F为圆心,AB、AC为半径画弧,两弧的交点为D,从而得到满足条件的△DCF;
(2)先利用全等三角形的性质得到DF=AC=4,CF=CB=2,∠DFC=∠ACB=90°,作FP的垂直平分线交PD于N,连接FN,作NH⊥DF于H,如图,证明MN=DF=BC,再证明△PMN≌△PCB,所以PC=PM,从而得到PC=CF.
【解题过程】
(1)解:如图,△DCF为所作;
(2)解:如图2,∵△DCF≌△ABC,
∴DF=AC=4,CF=CB=2,∠DFC=∠ACB=90°,
∴DFBC,
作FP的垂直平分线交PD于N,连接FN,作NH⊥DF于H,如图,
∴NP=NF,MP=MF,
∴∠NPF=∠NFP,
∴∠NDF=∠NFD,
∴ND=NF,
∴FH=DH
∵FH=MN,
∴MN=FH=DH=2,
∴MN=BC,
∵MNDF,
∴MNBC,
∴∠PMN=∠PCB,
在△PMN和△PCB中,
,
∴△PMN≌△PCB(AAS),
∴PC=PM,
而PM=MF,
∴PC=CF=.
17.(23-24八年级上·四川成都·开学考试)如图:在中,,,射线、的夹角为,过点作于点,直线交于点,连接.
(1)如图,若射线、都在的内部,且点与点关于对称,求证:;
(2)如图,若射线在的内部,射线在的外部,其他条件不变,求证:;
(3)如图,若射线、都在的外部,其他条件不变,若,,,求的长.
【思路点拨】
(1)先判断出,再用等式的性质判断出,进而判断出,即可得出结论;
(2)先判断出,再判断出,进而得出,即,即可得出结论;
(3)同(2)的方法判断出,最后用面积建立方程求出的值,即可得出结论.
【解题过程】
(1)证明:如图,连接,
,关于对称,
被垂直平分,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
;
(2)证明:如图,在上截取,连接,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
;
即;
(3)解:如图,延长至点,使,连接,
,
,
,
,
,
,
,
,
,
,
,
,
设,,
,,
,
,,
,
,
,
.
18.(23-24八年级上·辽宁·期中)在中,,,射线,的夹角为,过点作于点,直线交于点,连接.
(1)如图1,射线,都在内部.
①若,,则 ;
②作点关于直线的对称点,在图1中找出与线段相等的线段,并证明.
(2)如图2,射线在的内部,射线在的外部,其它条件不变,探究线段之间的数量关系,并证明.
【思路点拨】
(1)①先根据角的运算得出的度数,根据三角形内角和求出的度数;再根据直角三角形两锐角互余可得出的度数,作差可得结论;
②连接,可得出,再根据,,可得出,,所以;进而可得,再由全等三角形的性质可得结论;
(2)在延长线上取点,使.连接.由垂直平分线的性质可得,;设,,所以,由此表达,由,可得,所以,即;由此可得,所以,由此可得结论.
【解题过程】
(1)解:①,,,
,
,
,
,
,
,
,
,
故答案为:20;
②,理由如下:
证明:如图1,连接,
,
∵点与点关于直线对称,,
,
是的垂直平分线,
,
,
,
,
,,
,
,
,
;
(2)解:,
证明:如图2,在延长线上取点,使,连接,
,
,
,
设,
,
,
,
,
,
,
,
,即,
,
,
,
,
,
,
.
21世纪教育网(www.21cnjy.com)
正向思维:是一类常规性的、传统的思维形式,指的是大家按照自上而下,由近及远、从左到右、从可知到未知等一般而言的线性方向做出探究问题的思维途径。
逆向思维:是指在剖析、破解数学难题进程中,可以灵活转换思维方向,从常规思维的相反方向出发进行探索的思维方式,比如正向思维无法解决问题时可反其道而行采取逆向思维,直接证明有困难时可采用间接证明。
一、线段垂直平分线的性质
线段垂直平分线上的点与这条线段两个端点的距离相等.反过来,与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
二、线段垂直平分线的判定
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.(这样的点需要找两个)
【典例1】如图,的两条高与交于点,,.
(1)求证:;
(2)连结,试说明:是的垂直平分线;
(3)是射线上一点,且,动点从点出发,沿线段以每秒1个单位长度的速度向终点A运动,同时动点从点出发,沿射线以每秒3个单位长度的速度运动,当点到达点A时,,两点同时停止运动,设运动时间为秒,当与全等时,求的值.
【思路点拨】
(1)证明,即可得到;
(2)先证明,得到,进而得到点在的垂直平分线上,再根据得到点在的垂直平分线上,即可得到是的垂直平分线;
(3)当点在延长线上时,设运动秒,根据得到,,根据得到,进而得到,求得;当点在之间时,设运动秒,根据得到,,根据得到,进而得到,求得,问题得解.
【解题过程】
(1)证明:、是高,
,
在与中,
,
;
(2)证明:,,
,
,
、是高,
.
在与中,,
,
,
点在的垂直平分线上.
,
点在的垂直平分线上,
是的垂直平分线;
(3)解:①如图1,当点在延长线上时,
设运动秒,、分别运动到如图位置,.
,,
当时,.
,,
,
解得.
②如图2,当点在之间时,
设运动秒,、分别运动到如图位置,.
,,
当时,.
,,
,
解得.
综上所述,或4.
1.(22-23八年级上·山东聊城·期末)如图,线段,的垂直平分线,相交于点O.若,则( )
A. B. C. D.
2.(23-24八年级上·北京朝阳·阶段练习)如图,中,是的角平分线,延长至,使得,连接.下列判断:;;平分;的面积的面积,一定成立的个数是( )
A.个 B.个 C.个 D.个
3.(23-24八年级上·北京朝阳·期中)如图,在四边形中,点E,F分别在,边上,将沿折叠,使点落在点处,连接,.有下面四个结论:
①;②直线是线段的垂直平分线;③;④.
所有正确结论的序号为( )
A.①③ B.①②③ C.②③④ D.①②③④
4.(22-23八年级上·湖北武汉·阶段练习)如图,中,,是边的垂直平分线,交于G,过点F作于点E,平分交于F,连接,.下列结论:①②③④.其中正确的结论是( )
A.①②③ B.①②④ C.①③④ D.①②③④
5.(22-23八年级上·河北唐山·期中)如图,在中,,AD,BE分别为BC、AC边上的高,AD、BE相交于点F.下列结论:①;②;③;④若,则.正确的结论序号是( )
A.①② B.①②④ C.②③④ D.①③④
6.(23-24八年级上·江苏泰州·阶段练习)如图,中,,点M,N分别在,上,将沿直线翻折,点A的对应点D恰好落在边上(不含端点B,C),下列结论:①直线垂直平分;②;③;④若M是中点,则.其中一定正确的是( )
A.①② B.②③ C.①②④ D.①③④
7.(22-23八年级上·重庆巴南·期中)如图,在中,,以为边,作,满足,点为上一点,连接,,下列结论:①;②;③若,则;④.正确的有( )
A.1个 B.2个 C.3个 D.4个
8.(22-23七年级下·广西南宁·期末)如图,在中,D为中点,,,于点F,,,则的长为 .
9.(23-24八年级上·河北唐山·阶段练习)如图,在中,,,分别为,边上的高,,相交于点,连接,则下列结论:;;;若,则周长等于的长其中正确的有 写出所有正确结论的序号
10.(22-23八年级下·黑龙江哈尔滨·阶段练习)如图,在△ABC中,∠C=45°,AD⊥BC于D,F为AC上一点,连接BF交AD于E,过F作MN⊥FB交BA延长线于M,交BC于N,若点M恰在BN的垂直平分线上,且DE:BN=1:7,S△ABD=15,则S△ABE= .
11.(23-24八年级上·福建莆田·开学考试)如图,在中,,的角平分线和的平分线相交于点,交于点,交的延长线于点,过点作交的延长线于点,交的延长线于点,连接并延长交于点,则下列结论:①;②;③;④;其中正确的有 .(填序号)
12.(2023·江苏无锡·模拟预测)请用无刻度的直尺和圆规作图:
(1)如图1,在上求作点D,使;
(2)如图2,若点D在边上,在上求作点E,使.
13.(2023·江苏扬州·模拟预测)尺规作图:保留作图痕迹,不要求写作法.
(1)过点作一条直线,使其平分的面积.
(2)在上求作一点,使与面积相等.
(3)过点作一条直线,使其平分的面积.
14.(2024七年级下·全国·专题练习)如图,在中,,分别垂直平分边和边,交边于,两点,与相交于点.
(1)若,则的周长为 ;
(2)若,求的度数.
15.(22-23八年级上·江苏南京·阶段练习)如图,在中,垂直平分平分.
(1)若,求的度数;
(2)若,与的周长之差为,且的面积为,求的面积.
16.(22-23八年级上·福建福州·期中)如图,在△ABC中,∠ACB=90°.
(1)在AC的右侧作△DCF,使点F在AC上,且△DCF≌△ABC;(要求:尺规作图,保留作图痕迹)
(2)在(1)的条件下,连接BD交AC于点P.若AC=2BC=4,求PC的长.
17.(23-24八年级上·四川成都·开学考试)如图:在中,,,射线、的夹角为,过点作于点,直线交于点,连接.
(1)如图,若射线、都在的内部,且点与点关于对称,求证:;
(2)如图,若射线在的内部,射线在的外部,其他条件不变,求证:;
(3)如图,若射线、都在的外部,其他条件不变,若,,,求的长.
18.(23-24八年级上·辽宁·期中)在中,,,射线,的夹角为,过点作于点,直线交于点,连接.
(1)如图1,射线,都在内部.
①若,,则 ;
②作点关于直线的对称点,在图1中找出与线段相等的线段,并证明.
(2)如图2,射线在的内部,射线在的外部,其它条件不变,探究线段之间的数量关系,并证明.
21世纪教育网(www.21cnjy.com)
专题13.1 垂直平分线中的几何综合
正向思维:是一类常规性的、传统的思维形式,指的是大家按照自上而下,由近及远、从左到右、从可知到未知等一般而言的线性方向做出探究问题的思维途径。
逆向思维:是指在剖析、破解数学难题进程中,可以灵活转换思维方向,从常规思维的相反方向出发进行探索的思维方式,比如正向思维无法解决问题时可反其道而行采取逆向思维,直接证明有困难时可采用间接证明。
一、线段垂直平分线的性质
线段垂直平分线上的点与这条线段两个端点的距离相等.反过来,与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
二、线段垂直平分线的判定
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.(这样的点需要找两个)
【典例1】如图,的两条高与交于点,,.
(1)求证:;
(2)连结,试说明:是的垂直平分线;
(3)是射线上一点,且,动点从点出发,沿线段以每秒1个单位长度的速度向终点A运动,同时动点从点出发,沿射线以每秒3个单位长度的速度运动,当点到达点A时,,两点同时停止运动,设运动时间为秒,当与全等时,求的值.
【思路点拨】
(1)证明,即可得到;
(2)先证明,得到,进而得到点在的垂直平分线上,再根据得到点在的垂直平分线上,即可得到是的垂直平分线;
(3)当点在延长线上时,设运动秒,根据得到,,根据得到,进而得到,求得;当点在之间时,设运动秒,根据得到,,根据得到,进而得到,求得,问题得解.
【解题过程】
(1)证明:、是高,
,
在与中,
,
;
(2)证明:,,
,
,
、是高,
.
在与中,,
,
,
点在的垂直平分线上.
,
点在的垂直平分线上,
是的垂直平分线;
(3)解:①如图1,当点在延长线上时,
设运动秒,、分别运动到如图位置,.
,,
当时,.
,,
,
解得.
②如图2,当点在之间时,
设运动秒,、分别运动到如图位置,.
,,
当时,.
,,
,
解得.
综上所述,或4.
1.(22-23八年级上·山东聊城·期末)如图,线段,的垂直平分线,相交于点O.若,则( )
A. B. C. D.
【思路点拨】
根据线段垂直平分线的性质结合三角形外角性质得到,再利用垂直的定义结合直角三角形两锐角互余得到,计算即可.
【解题过程】
解:如图,连接BO并延长至点P,与线段AB交于F,
∵,是、的垂直平分线,
∴,,,
∴,
∴,,
∴,
∵,,
∴,
∴,
故选:B
2.(23-24八年级上·北京朝阳·阶段练习)如图,中,是的角平分线,延长至,使得,连接.下列判断:;;平分;的面积的面积,一定成立的个数是( )
A.个 B.个 C.个 D.个
【思路点拨】
利用三角形的角平分线,中线和垂直平分线进行判断即可,
【解题过程】
解:如图,延长交于点,过作于点,
∵,,
∴,
又∵是的平分线,
∴垂直平分,
∴,故正确;
∵,
∴,,
∴,即,故正确;
由题意可知与不一定相等,
则不一定成立;
∵,垂直平分,
∴,
∴,故正确;
综上 正确;
故选:.
3.(23-24八年级上·北京朝阳·期中)如图,在四边形中,点E,F分别在,边上,将沿折叠,使点落在点处,连接,.有下面四个结论:
①;②直线是线段的垂直平分线;③;④.
所有正确结论的序号为( )
A.①③ B.①②③ C.②③④ D.①②③④
【思路点拨】
本题考查翻折变换,线段垂直平分线的判定,多边形内角和公式,三角形外角性质,掌握翻折不变性,以及相关性质是解题的关键.
由翻折不变性,可判断①正确;由翻折不变性,可得,,可判断②正确;由多边形内角和公式和翻折不变性,可判断③正确;由三角形外角性质和翻折不变性,可判断④正确;即可解答.
【解题过程】
解: 是由翻折得到的,
,
故①正确;
是由翻折得到的,是由翻折得到的,
,,
点E,点F都在的垂直平分线上,
直线是线段的垂直平分线,
故②正确;
是由翻折得到的,
故③正确;
设与交于点H,
是由翻折得到的,
故④正确;
综上,正确的有:①②③④,
故选:D.
4.(22-23八年级上·湖北武汉·阶段练习)如图,中,,是边的垂直平分线,交于G,过点F作于点E,平分交于F,连接,.下列结论:①②③④.其中正确的结论是( )
A.①②③ B.①②④ C.①③④ D.①②③④
【思路点拨】
根据线段垂直平分线的性质,得到;过点F作于点H,证明,得到,结合平分,得到,继而,可证明;利用斜边大于直角边,证明;利用等腰三角形的性质,全等三角形的性质,结合三角形内角和定理证明.
【解题过程】
解:∵是边的垂直平分线,
∴;
故①正确;
过点F作于点H,
∵平分,,,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
故③正确;
∵,
∴,
∴,
∴,
故②正确;
∵,,
∴,
∴,
故④正确;
故选D.
5.(22-23八年级上·河北唐山·期中)如图,在中,,AD,BE分别为BC、AC边上的高,AD、BE相交于点F.下列结论:①;②;③;④若,则.正确的结论序号是( )
A.①② B.①②④ C.②③④ D.①③④
【思路点拨】
根据垂直定义可得,再利用,得到,从而可证明,进而得到,即可判断①;根据,,即可判断②,根据三角形面积公式和它们有一条公共边可得,即可判断③,若,根据可以得到,从而可得是的中点,然后可以推出是的垂直平分线,最后由线段垂直平分线的性质即可判断④.
【解题过程】
解:,
,
,
,
,
,
,
,
,
,
,
,
,故①正确;
,,
,故②不正确;
,
,故③正确;
,
,
,
为的中点,
,
为线段的垂直平分线,
,故④正确,
所以,正确结论的序号是:①③④,
故选:D.
6.(23-24八年级上·江苏泰州·阶段练习)如图,中,,点M,N分别在,上,将沿直线翻折,点A的对应点D恰好落在边上(不含端点B,C),下列结论:①直线垂直平分;②;③;④若M是中点,则.其中一定正确的是( )
A.①② B.②③ C.①②④ D.①③④
【思路点拨】
①根据将沿直线翻折,点A的对应点D恰好落在边上(不含端点B,C),证明直线垂直平分,故①正确;
②证明与不一定相等,得到与不一定相等,故②错误;
③先由①得,直线垂直平分,则,,再根据”等边对等角“证明,,则,再根据是的一个外角,是的一个外角,证明,,进一步证明,根据,得到,则,然后根据,证明,从而得到,故③正确;
④先根据是的中点,证明,再由①得,直线垂直平分,则,再证明,最后证明,即,故④正确.
【解题过程】
解:①∵将沿直线翻折,点A的对应点D恰好落在边上(不含端点B,C),
∴直线垂直平分,
故①正确;
②∵,
∴,
∴
又∵,
∴与不一定相等,
∴与不一定相等,
∴与不一定相等,
故②错误;
③由①得,直线垂直平分,
∴,,
∴,,
∴
∵是的一个外角,是的一个外角,
∴,
∴,
∴,
∴,
∴,
∴
又∵,
∴
即,
又∵(已证),
∴,
故③正确;
④∵是的中点,
∴,
∵,
∴,
∴,,
又,
∴,
∴,
∴,
故④正确;
综上所述,一定正确的有①③④,
故选:D.
7.(22-23八年级上·重庆巴南·期中)如图,在中,,以为边,作,满足,点为上一点,连接,,下列结论:①;②;③若,则;④.正确的有( )
A.1个 B.2个 C.3个 D.4个
【思路点拨】
延长至G,使,从而得到,进一步证明,且,利用证明,则,所以①是正确的,通过线段的等量代换运算推导出④是正确的,设,则,因为,所以,接着用x表示出,再计算出,故③是正确的,当时,可以推导出,否则不垂直于,故②是错误的.
【解题过程】
解:如图,延长至G,使,设与交于点M,
∵,
∴,
∴垂直平分,
∴,
∴,
∵,
∴,
∴,
∴,
在中,
,
∴,
∴,
∴①是正确的;
∵,
∴,
∴平分,
当时,,则,
当时,,则无法说明,
∴②是不正确的;
设,则,
∴,
∵,
∴,
∴,
∴,
∴,
∴③是正确的;
∵,
∴,
∵,
∴,
∴
∴④是正确的,
故选:C.
8.(22-23七年级下·广西南宁·期末)如图,在中,D为中点,,,于点F,,,则的长为 .
【思路点拨】
连接,过点E作,交的延长线于N,由,可得;由D为中点,,则可得;证明,再证明即可求得结果.
【解题过程】
解:连接,过点E作,交的延长线于N,如图,
∵,,
∴;
∵D为中点,,
∴;
∵,,
∴,
∵,
∴,
∴;
∵,,,
∴,
∴,
∴,
即,
∴.
∴
故答案为:.
9.(23-24八年级上·河北唐山·阶段练习)如图,在中,,,分别为,边上的高,,相交于点,连接,则下列结论:;;;若,则周长等于的长其中正确的有 写出所有正确结论的序号
【思路点拨】
本题考查了全等三角形的判定与性质,掌握全等三角形的判定与性质,线段垂直平分线的性质,外角的性质,三角形内角和定理,等腰三角形的性质是解决问题的关键.
延长交于,先利用“”证明,得出,,可判断①符合题意;由,得出,再由三角形外角的性质,可判断②不符合题意;由,,得出,得出,可判断③符合题意;由,,可证明垂直平分,得出,,得出的周长,可判断④符合题意;即可得出答案.
【解题过程】
解:如图,延长交于,
,分别为,边上的高,
,
,
,
,
,
,
,
在和中,
,
,
,,故①符合题意;
,
,
,
,故②不符合题意;
,,
,
,故③符合题意;
,,
,
,
,
垂直平分,
,,
的周长
,故④符合题意.
故答案为:.
10.(22-23八年级下·黑龙江哈尔滨·阶段练习)如图,在△ABC中,∠C=45°,AD⊥BC于D,F为AC上一点,连接BF交AD于E,过F作MN⊥FB交BA延长线于M,交BC于N,若点M恰在BN的垂直平分线上,且DE:BN=1:7,S△ABD=15,则S△ABE= .
【思路点拨】
过点F作FG⊥BN于点G,根据已知条件证明△ABD≌△BFG,可得BD=FG,AD=BG,再证明△BDE≌△FGN可得DE=GN,根据DE:BN=1:7,可得GN:BN=1:7,设ED=x,DE:BG=1:6,可得AD=BG=6x, AE=5x,然后根据S△ABD=15,进而可得S△ABE.
【解题过程】
解:如图,过点F作FG⊥BN于点G,
∵AD⊥BC,
∴∠ADC=90°,
∵∠C=45°,
∴∠DAC=45°,
∵MN⊥FB,
∴∠FBN+∠FNB=90°,
∵点M恰在BN的垂直平分线上,
∴MB=MN,
∴∠ABN=∠FNB,
∴∠ABN+∠BAD=90°,
∴∠BAD=∠FBN,
∵∠AFB=∠FBC+∠C=∠BAD+∠DAC=∠BAF,
∴BA=BF,
在△ABD和△BFG中,
,
∴△ABD≌△BFG(AAS),
∴BD=FG,AD=BG,
∵∠BED+∠EBD=90°,∠BAD+∠ABD=90°,
∴∠BED=∠ABD=∠BFG=∠FNG,
在△BDE和△FGN中,
,
∴△BDE≌△FGN(AAS),
∴DE=GN,
∵DE:BN=1:7,
∴GN:BN=1:7,
设ED=x,
∴DE:BG=1:6,
∴AD=BG=6x,
∴AE=AD﹣ED=6x﹣x=5x,
∵S△ABD=15,
∴S△ABE==.
故答案为:.
11.(23-24八年级上·福建莆田·开学考试)如图,在中,,的角平分线和的平分线相交于点,交于点,交的延长线于点,过点作交的延长线于点,交的延长线于点,连接并延长交于点,则下列结论:①;②;③;④;其中正确的有 .(填序号)
【思路点拨】
①利用角平分线的性质以及三角形外角的性质,求解即可;
②③延长与交于点,利用全等三角形的判定与性质求解即可;
④在上截取,利用垂直平分线的性质以及全等三角形的性质,求解即可.
【解题过程】
解:设,,
∵平分,平分,
∴,
由三角形外角的性质可得:
∴①正确;
延长与交于点,如下图:
∵
∴
∵平分
∴
又∵,
∴
∴
∵
∴
又∵,
∴
∴
∴②正确;
同理可得:
∴,③正确;
在上截取,则是的垂直平分线,如下图:
∴
∵
∴,
又∵
∴
∵,
∴
∵
∴
∴
又∵
∴
又∵
∴
∴
∴④正确
故答案为:①②③④
12.(2023·江苏无锡·模拟预测)请用无刻度的直尺和圆规作图:
(1)如图1,在上求作点D,使;
(2)如图2,若点D在边上,在上求作点E,使.
【思路点拨】
(1)作的垂直平分线与的交点即为所求;
(2)如图:由题意得,只要作即可,由第(1)问得,,只要作即可.
【解题过程】
(1)解:如图:
作的垂直平分线与交于D点,
,
与高相同,
.
如图1:点D即为所求;
(2)如图:
由题意得,只要作即可,
作的垂直平分线交于点,
由第(1)问得,,
故只要作即可,
连接、,要使得,只要作,
根据“夹在平行线之间的垂线段相等”,即,高相等,
只要作,
根据“同位角相等,两直线平行”,作,交于点,
如图2:点E即为所求.
13.(2023·江苏扬州·模拟预测)尺规作图:保留作图痕迹,不要求写作法.
(1)过点作一条直线,使其平分的面积.
(2)在上求作一点,使与面积相等.
(3)过点作一条直线,使其平分的面积.
【思路点拨】
(1)作出线段的垂直平分线,垂足为,作直线即可;
(2)作,交与点,点即为所求;
(3)根据(1)的方法作出中线,连接,根据(2)的方法作,交与点,作直线即可.
【解题过程】
(1)解: 如图直线即为所求;
(2)解: 如图,点即为所求;
∵,
∴,
∴,
(3)解:如图,直线即为所求.
理由如下,
∵是的中线,
∴,
∵,
∴,
∴,
∴直线平分的面积.
14.(2024七年级下·全国·专题练习)如图,在中,,分别垂直平分边和边,交边于,两点,与相交于点.
(1)若,则的周长为 ;
(2)若,求的度数.
【思路点拨】
本题考查垂直平分线,三角形内角和的知识,解题的关键是掌握垂直平分线的性质,三角形的内角和,即可.
(1)根据垂直平分线的性质,则,,根据,的周长为:,即可;
(2)垂直平分线的性质,则,,根据三角形内角和,则,再根据对顶角相等,则,根据三角形内角和,则,,最后根据,即可.
【解题过程】
(1)∵,分别垂直平分边和边,
∴,,
∵,
∴,
∵的周长为:,
∴,
故答案为:.
(2)∵,分别垂直平分边和边,
∴,,
∵,
∴,
∵,,
∴,
∵,,
∴,
∴,
∴,
∴.
15.(22-23八年级上·江苏南京·阶段练习)如图,在中,垂直平分平分.
(1)若,求的度数;
(2)若,与的周长之差为,且的面积为,求的面积.
【思路点拨】
(1)由线段垂直平分线的性质结合三角形外角的性质易求出,再根据角平分线的定义即得出,最后根据三角形内角和定理求解即可;
(2)由线段垂直平分线的性质结合与的周长之差为,即可求出.过点D作于H.由的面积为,,可求出,结合角平分线的性质定理可得出,即可计算.
【解题过程】
(1)解:∵垂直平分,
∴,
∴.
∵,
∴.
∵平分,
∴,
∴;
(2)解:∵垂直平分,
∴,,,
∵,,,
∴,
∴,
∴,即.
过点D作于H.
∵的面积为,且,,
∴,
∴.
∵平分,
∴.
∴.
16.(22-23八年级上·福建福州·期中)如图,在△ABC中,∠ACB=90°.
(1)在AC的右侧作△DCF,使点F在AC上,且△DCF≌△ABC;(要求:尺规作图,保留作图痕迹)
(2)在(1)的条件下,连接BD交AC于点P.若AC=2BC=4,求PC的长.
【思路点拨】
(1)在CA上截取CF=CB,然后分别以C、F为圆心,AB、AC为半径画弧,两弧的交点为D,从而得到满足条件的△DCF;
(2)先利用全等三角形的性质得到DF=AC=4,CF=CB=2,∠DFC=∠ACB=90°,作FP的垂直平分线交PD于N,连接FN,作NH⊥DF于H,如图,证明MN=DF=BC,再证明△PMN≌△PCB,所以PC=PM,从而得到PC=CF.
【解题过程】
(1)解:如图,△DCF为所作;
(2)解:如图2,∵△DCF≌△ABC,
∴DF=AC=4,CF=CB=2,∠DFC=∠ACB=90°,
∴DFBC,
作FP的垂直平分线交PD于N,连接FN,作NH⊥DF于H,如图,
∴NP=NF,MP=MF,
∴∠NPF=∠NFP,
∴∠NDF=∠NFD,
∴ND=NF,
∴FH=DH
∵FH=MN,
∴MN=FH=DH=2,
∴MN=BC,
∵MNDF,
∴MNBC,
∴∠PMN=∠PCB,
在△PMN和△PCB中,
,
∴△PMN≌△PCB(AAS),
∴PC=PM,
而PM=MF,
∴PC=CF=.
17.(23-24八年级上·四川成都·开学考试)如图:在中,,,射线、的夹角为,过点作于点,直线交于点,连接.
(1)如图,若射线、都在的内部,且点与点关于对称,求证:;
(2)如图,若射线在的内部,射线在的外部,其他条件不变,求证:;
(3)如图,若射线、都在的外部,其他条件不变,若,,,求的长.
【思路点拨】
(1)先判断出,再用等式的性质判断出,进而判断出,即可得出结论;
(2)先判断出,再判断出,进而得出,即,即可得出结论;
(3)同(2)的方法判断出,最后用面积建立方程求出的值,即可得出结论.
【解题过程】
(1)证明:如图,连接,
,关于对称,
被垂直平分,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
;
(2)证明:如图,在上截取,连接,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
;
即;
(3)解:如图,延长至点,使,连接,
,
,
,
,
,
,
,
,
,
,
,
,
设,,
,,
,
,,
,
,
,
.
18.(23-24八年级上·辽宁·期中)在中,,,射线,的夹角为,过点作于点,直线交于点,连接.
(1)如图1,射线,都在内部.
①若,,则 ;
②作点关于直线的对称点,在图1中找出与线段相等的线段,并证明.
(2)如图2,射线在的内部,射线在的外部,其它条件不变,探究线段之间的数量关系,并证明.
【思路点拨】
(1)①先根据角的运算得出的度数,根据三角形内角和求出的度数;再根据直角三角形两锐角互余可得出的度数,作差可得结论;
②连接,可得出,再根据,,可得出,,所以;进而可得,再由全等三角形的性质可得结论;
(2)在延长线上取点,使.连接.由垂直平分线的性质可得,;设,,所以,由此表达,由,可得,所以,即;由此可得,所以,由此可得结论.
【解题过程】
(1)解:①,,,
,
,
,
,
,
,
,
,
故答案为:20;
②,理由如下:
证明:如图1,连接,
,
∵点与点关于直线对称,,
,
是的垂直平分线,
,
,
,
,
,,
,
,
,
;
(2)解:,
证明:如图2,在延长线上取点,使,连接,
,
,
,
设,
,
,
,
,
,
,
,
,即,
,
,
,
,
,
,
.
21世纪教育网(www.21cnjy.com)
